Также в отдельных случаях называется колебательным или К-звеном. Примером физической реализации данного звена может являться система из двух сообщающихся баков с водой без насосов на стоке и притоке, если входом является перемещение клапана на притоке, а выходом - уровень во втором баке.

Дифференциальное уравнение инерционного звена второго порядка имеет вид, приведенный ниже: .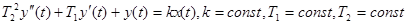

Коэффициент передачи данного звена обозначается k и имеет размерность, равную отношению размерности выходного сигнала к размерности входного. Т₁ и Т₂ - это постоянные времени звена, соответственно, они имеют размерность времени.

Передаточная функция звена имеет вид: .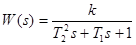

КЧХ звена имеет вид: .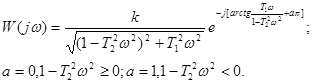

АЧХ звена имеет вид: .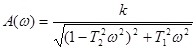

ФЧХ ИД-звена имеет вид: .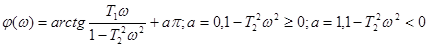

Вид переходной характеристики инерционного звена второго порядка зависит от вида корней характеристического уравнения звена, то есть, от соотношения постоянных времени Т₁ и T₂.

Если корни действительные и различные (-α₁;-α₂), то переходная характеристика имеет вид:

.

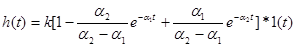Если корни вещественные и равные (-α), то переходная характеристика будет иметь вид:

.

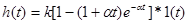Если корни являются комплексно-сопряженными (-α±jω)

.

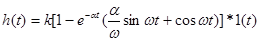В последнем случае переходная характеристика имеет колебательный характер.

Для систем с колебательностью также характерен пик на АЧХ на частоте колебаний. Затухание колебаний можно характеризовать корневым показателем колебательности, частотным показателем колебательности или степенью затухания.

Звено запаздывания

Также называется З-звеном. Примером физической реализации данного звена может являться транспортер.

Переходная характеристика З-звена имеет вид: .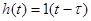

КЧХ З-звена имеет вид: .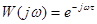

АЧХ З-звена имеет вид: А(ω)=1.

ФЧХ З-звена имеет вид: φ(ω)=-ωτ.

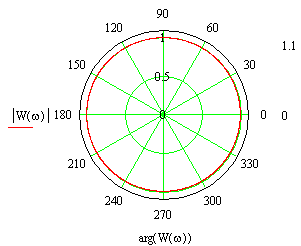
Вид годографа КЧХ З-звена приведен на рис. 9-10.

Рис. 3-20. Пример годографа КЧХ звена запаздывания.

Типовые соединения элементарных звеньев

Существует четыре вида соединений звеньев

- последовательное;

- параллельное;

- встречно-параллельное (с обратной связью);

- смешанное (может включать некоторые или все предыдущие виды).

Рассмотрим ниже перечисленные соединения звеньев.

Последовательное соединение

Последовательное соединение звеньев показано на рис. 10-1

Рис. 3-21. Последовательное соединение звеньев.

При последовательном соединении звеньев передаточная функция системы представляет собой произведение передаточных функций составляющих:

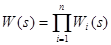.                                                         (10-1)

Аналогично можно найти КЧХ данной системы:

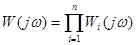.                                                      (10-2)

Тогда АЧХ и ФЧХ можно найти, соответственно, по формулам:

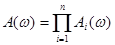                                                         (10-3)

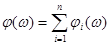                                                         (10-4)

В данном случае при построении годографа КЧХ удобнее сначала построить графики АЧХ и ФЧХ, а затем строить годограф. Необходимо так же заметить, что переходную характеристику в данном случае можно найти, например, через интеграл свертки. Перемножать переходные характеристики составляющих ни в коем случае нельзя.

Параллельное соединение

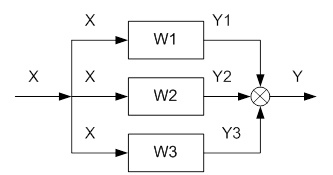
Параллельное соединение звеньев показано на рис. 10-2.

Рис. 3-22. Параллельное соединение звеньев.

Для параллельного соединения звеньев передаточная функция системы ищется по формуле:

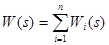                                                            (10-5)

Аналогично можно найти КЧХ:

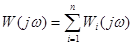                                                         (10-6)

При построении годографа КЧХ параллельного соединения звеньев, зная годографы составляющих, складывают векторы на соответствующих частотах по правилу параллелограмма. В данном случае удобнее сначала найти годограф КЧХ и по нему строить графики АЧХ и ФЧХ.

Переходную характеристику всей системы так же можно найти, сложив переходные характеристики составляющих.