Статические и динамические системы

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Лекция 3

Динамические системы и их математические модели.
Автоматические системы регулирования

Список источников

[1] Главы 2,4

[1] Главы 5-7

1. Статические и динамические системы.

2. Линейные и нелинейные системы.

3. Дифференциальные уравнения динамических систем.

4. Типовые воздействия и реакции на них.

5. Интеграл свертки.

6. Преобразование Лапласа (прямое и обратное) и передаточная функция.

7. Элементарные звенья: перечень, пример.

8. Математические модели объектов управления.

Статические и динамические системы

Переходные динамические характеристики линейных систем

Линейные динамические системы имеют два отличительных признака: они описываются ЛДУ, и для них справедлив принцип наложения (суперпозиций).

Принцип суперпозиций заключается в следующем. Если на входе в динамическую систему имеется воздействие, представляющее собой сумму некоторых воздействий ( 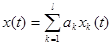), то реакция системы на данное воздействие представляет собой сумму реакций на каждое воздействие ( ).

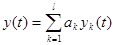Для исследования линейных систем применим не только метод дифференциальных уравнений, но и другие методы. Например, свойства этих систем можно описывать с помощью динамических характеристик.

Динамическая характеристика – это характеристика, определяющая реакцию системы на некоторые типовые входные воздействия (их также называют тестовыми воздействиями).

Подбор тестовых воздействий осуществляется таким образом, чтобы любое возможное в процессе эксплуатации воздействие на систему можно было представить взвешенной суммой типовых воздействий. Таким образом, используя принцип наложения можно определить реакцию системы на любое воздействие.

Типовые воздействия

Существует несколько видов типовых воздействий.

Единичное ступенчатое воздействие (функция Хевисайда);
Дельта-функция, функция Дирака;
Гармонические колебания единичной амплитуды.

Переходная характеристика – это реакция объекта/системы на функцию Хевисайда.

Импульсная переходная характеристика – реакция объекта/системы на дельта-функцию.

Кривая разгона – реакция объекта/системы на ступенчатое воздействие произвольной величины.

Необходимо иметь в виду следующее. Пусть функция f(t) определена на (-∞,∞), тогда:

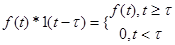; (3-21)

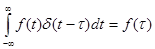. (3-22)

Интеграл свертки

Покажем, что имею любую из описанных динамических характеристик (переходную или импульсную характеристику), можно вычислить реакцию линейной системы на входное воздействие произвольного вида.

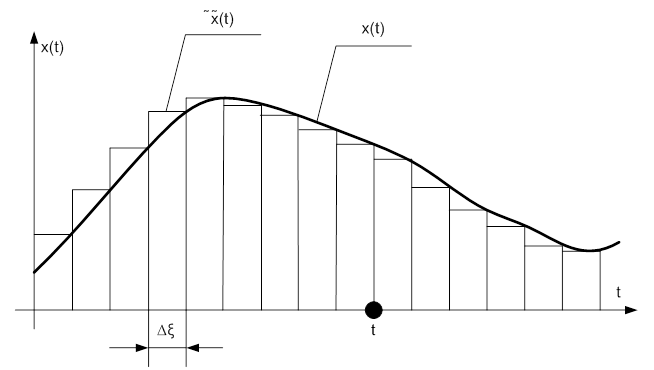
Пусть на входе в динамическую систему имеется произвольное входное воздействие x(t). График зависимости от времени входного воздействия приведен на рис. 5-1.

Рис. 3-1. График зависимости от времени входного воздействия.

Найдем значение выхода системы в произвольный момент времени t (этот момент произволен, но зафиксирован).

Разобьем ось времени на небольшие отрезки длительностью Δξ, далее построим новую функцию времени 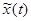, совпадающую с исходной в точках разбиения и остающуюся постоянной в промежутках между ними. Можно записать, что

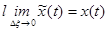. (3-23)

При этом 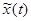- это последовательность прямоугольных импульсов длительностью Δξ, таким образом, реакцию линейной системы на 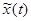можно вычислить как сумму реакций на каждый импульс, взятый отдельно.

Пусть 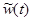- реакция системы на прямоугольный импульс длительностью Δξ и амплитудой 1/Δξ (то есть, на импульс единичной площади). Тогда, если импульсы имеют амплитуду А, то можно записать .

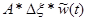Тогда реакция системы (у(t)) в фиксированный момент времени t на последовательность импульсов ( 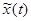) можно вычислить по формуле (принцип наложения):

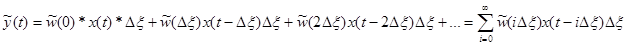. (3-24)

Точное решение можно найти при 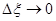, тогда 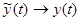, , 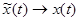, 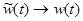а сумма переходит в интеграл. Таким образом, можно записать:

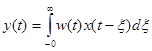. (3-25)

ИПХ должна удовлетворять условию физической реализуемости, то есть, равняться нулю при t<0, поэтому без потери смысла можно записать выражение 5-5 следующим образом:

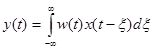. (3-26)

Если воздействие внезапно приложено в нулевой момент времени, и начальные условия нулевые, то можно записать:

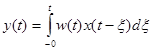. (3-27)

Выражение (5-7) называется интеграл свертки.

Если входное воздействие представляет собой функцию Хевисайда, то можно получить выражение для переходной характеристики:

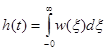. (3-28)

Необходимо заметить, что ИПХ – это производная от ПХ.

Из интеграла свертки следует, что выходная величина динамической системы в некоторый момент времени зависит не только от входного воздействия в этот момент времени, но и в предыдущие моменты времени. То есть, динамическая система обладает «памятью» на входные воздействия, статическая – не обладает.

Спектральное представление сигналов. Преобразование Фурье

Любую функцию времени можно представить в виде суммы соответствующим образом подобранных гармонических колебаний вида:

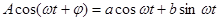(3-29)

где: 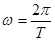- угловая частота колебаний;

Т – период колебаний;

А - амплитуда колебаний;

φ – начальная фаза колебаний.

Графики колебаний показаны на рис. 6-1.

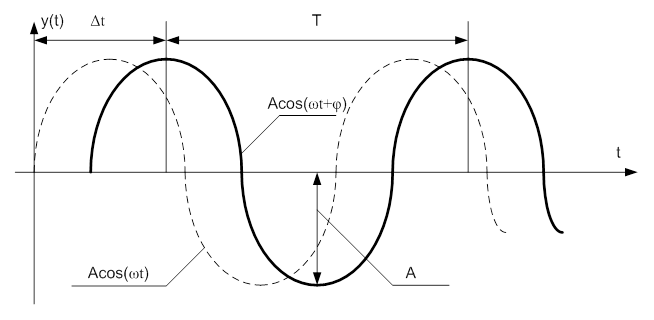
Рис. 3-2. Колебания на входе и на выходе в систему.

Можно записать, что: 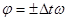, при этом 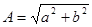и

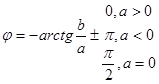(3-30)

Пусть имеется функция произвольного вида x(t), которую нужно представить в виде суммы гармоник. График функции показан на рис. 6-2.

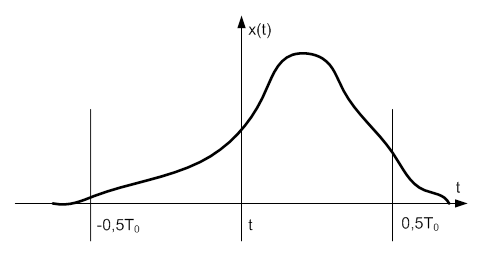
Рис. 3-3. График произвольной функции x(t).

Выберем период Т₀ и построим новую функцию 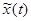, имеющую указанный период и совпадающую с исходной на отрезке 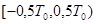. Если функция 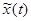удовлетворяет условию 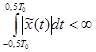, то её можно представить рядом Фурье, то есть суммой гармоник с частотами ω₀, 2ω₀, 3ω₀ (то есть, с частотами, кратными 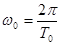). Тогда функция 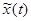будет иметь вид:

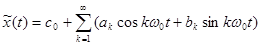. (3-31)

Формула 6-3 представляет собой ряд Фурье, коэффициенты этого ряда определяются формулами:

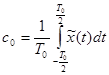, (3-32)

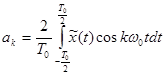, (3-33)

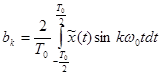. (3-34)

С учетом формул (6-4)-(6-6) ряд Фурье можно записать в виде:

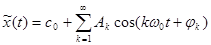. (3-35)

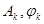- амплитуда и начальная фаза k-ой гармоники.

Совокупность чисел 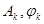называется амплитудным и фазовым спектрами функции 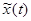, где k – целое положительное число. Разложение функции 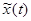в ряд Фурье называется спектральным разложением .

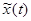С учетом известной формулы Эйлера можно получить

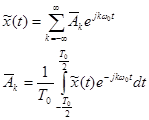; (3-36)

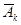- комплексное число, полностью определяющее к-ую гармонику разложения. Связь 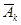с амплитудой и начальной фазой к-ой гармоники определяется формулой:

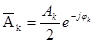. (3-37)

Чтобы получить разложение на гармоники исходной непериодической функции нужно устремить принятый период Т₀ к бесконечности. При этом аплитуды гармоник будут стремиться к нулю (см. формулы 6-7 и 6-8), поэтому необходимо ввести новые комплексные коэффициенты разложения:

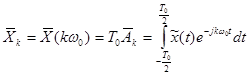. (3-38)

При этом изменится вид (6-7):

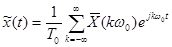. (3-39)

С учетом того, что разность частот соседних гармоник равна ω₀, получим:

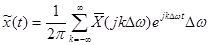. (3-40)

При стремлении Т₀ к бесконечности в итоге получим:

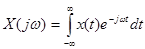(3-41)

Формула (6-12) представляет собой прямое преобразование Фурье. Нижеследующая формула (6-13) представляет собой обратное преобразование Фурье:

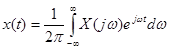. (3-42)

Прямое и обратное преобразования Фурье обозначаются соответственно:

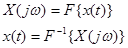. (3-43)

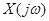- изображение исходной функции по Фурье, комплексная функция частоты. Модуль изображения по Фурье от x(t) является распределением по частотам амплитуд гармоник в разложении x(t). Изображение по Фурье от x(t) называется комплексной спектральной плотностью x( t).

Физический смысл КЧХ

С учетом формулы Эйлера сигналы на входе и выходе можно записать в виде:

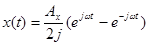; (3-44)

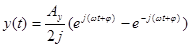. (3-45)

В соответствии с принципом наложения можем рассмотреть только первые слагаемые формул (7-1) и (7-2), для вторых слагаемых вывод будет аналогичен.

Пусть система описывается дифференциальным уравнением вида:

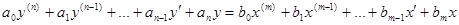(3-46)

Подставим в (7-3) первые слагаемые из (7-1) и (7-2) на место входного и выходного воздействий соответственно. После выполнения арифметических преобразований получим:

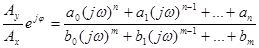. (3-47)

Аналогичное соотношение можно получить, если подставить в (7-3) вторые слагаемые из (7-1) и (7-2). Если сопоставить (7-4) с выражением для передаточной функции, то окажется, что:

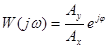. (7-5)

Из (7-5) видно, что:

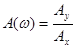, (7-6)

то есть, это АЧХ, а φ - это ФЧХ.

АЧХ, амплитудно-частотная характеристика – это зависимость отношения амплитуды колебаний на выходе к амплитуде колебаний на входе в систему от частоты колебаний.

ФЧХ, фазо-частотная характеристика – это зависимость от частоты сдвига фаз между входными и выходными колебаниями.

Физический смысл АЧХ и ФЧХ следует из их определений. Из физического смысла АЧХ и ФЧХ складывается физический смысл КЧХ. Согласно определению, КЧХ (комплексная частотная характеристика) некоторой системы - это комплексная функция частоты, модуль которой является АЧХ системы, а аргумент – ФЧХ.

Можно показать, что вещественная часть КЧХ – это четная функция частоты:

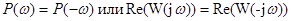. (7-7)

Также можно показать, что мнимая часть КЧХ – это нечетная функция частоты:

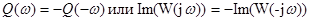. (7-8)

Таким образом, ветвь КЧХ при отрицательных частотах является зеркальным отражением ветки КЧХ при положительных частотах относительно действительной оси, поэтому годограф КЧХ при отрицательных частотах обычно не строят.

Разностные уравнения

Выходной сигнал динамической системы можно вычислить (численно) с помощью разностных уравнений. Пусть имеется дифференциальное уравнение некой динамической системы:

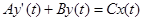
Решим это уравнение по численному методу Эйлера:

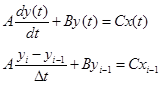
Последнее уравнение называется разностное уравнение. Выразим из последнего уравнения y_i.

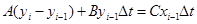
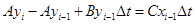
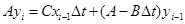
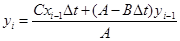
Таким образом, зная входное воздействие и значение выхода системы в предыдущий (или предыдущие) моменты времени, можно найти значение выходной величины в текущий момент времени.

Элементарные звенья

- статическое (безинерционное, пропорциональное, П);

- интегрирующее (И);

- дифференцирующее (идеальное дифференцирующее, Д);

- реальное дифференцирующее (РД);

- инерционное звено первого порядка (апериодическое, А);

- звено запаздывания (З);

- интегродифференцирующее (ИД);

- инерционное звено второго порядка (колебательное, К).

Инерционное звено второго порядка (или колебательное звено) описывается дифференциальным уравнением второго порядка, тем не менее, его тоже относят к элементарным звеньям.

Статическое звено

Также называется безинерционным, пропорциональным или П-звеном. Примером физической реализации П-звена является рычаг, клапаны с линеаризованными характеристиками, пружина обратной связи в гидравлическом регуляторе и т.д.

Дифференциальное уравнение П-звена имеет вид: .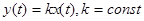

Коэффициент k в дифференциальном уравнении П-звена называется также коэффициентом передачи П-звена. Необходимо заметить, что это размерная величина, размерность которой представляет собой отношение размерности выходного сигнала к размерности входного сигнала.

Передаточная функция П-звена имеет вид: .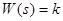

КЧХ П-звена имеет вид: .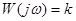

АЧХ П-звена имеет вид: .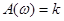

ФЧХ П-звена имеет вид: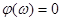

Переходная характеристика П-звена имеет вид: .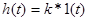

Импульсная переходная характеристика П-звена имеет вид: .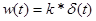

Графики всех упомянутых функций тривиальны, поэтому приводить их здесь нет необходимости.

Интегрирующее звено

Также называется И-звеном. Примером физической реализации И-звена является гидравлический исполнительный двигатель или гидравлическая система (бак) с насосом на стоке.

Дифференциальное уравнение И-звена имеет вид: .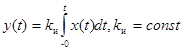

Коэффициент k_и в дифференциальном уравнении И-звена называется также коэффициентом передачи И-звена. Необходимо заметить, что это размерная величина, размерность которой представляет собой отношение размерности выходного сигнала, к размерности входного сигнала, умноженной на время.

Передаточная функция И-звена имеет вид: .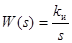

КЧХ И-звена имеет вид: .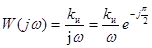

АЧХ И-звена имеет вид: .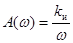

ФЧХ И-звена имеет вид: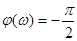

Переходная характеристика И-звена имеет вид: .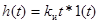

Импульсная переходная характеристика И-звена имеет вид: .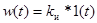

Годограф КЧХ И-звена представлен на рис. 8-1.

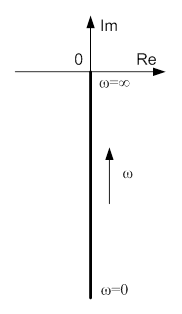
Рис. 3-4. Годограф КЧХ И-звена.

Дифференцирующее звено

Также называется идеальным дифференцирующим или Д-звеном. Идеальное дифференцирующее звено нельзя реализовать физически, так как в его дифференциальном уравнении порядок левой части меньше порядка правой.

Дифференциальное уравнение Д-звена имеет вид: .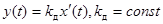

Коэффициент k_д в дифференциальном уравнении Д-звена называется также коэффициентом передачи Д-звена. Необходимо заметить, что это размерная величина, размерность которой представляет собой отношение размерности выходного сигнала, умноженной на время, к размерности входного сигнала.

Передаточная функция Д-звена имеет вид: .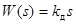

КЧХ Д-звена имеет вид: .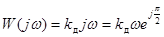

АЧХ Д-звена имеет вид: .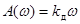

ФЧХ Д-звена имеет вид: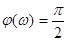

Переходная характеристика Д-звена имеет вид: .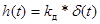

Годограф КЧХ идеального дифференцирующего звена приведен на рис. 8-2.

Рис. 3-5. Годограф КЧХ идеального дифференцирующего звена.

Реальное дифференцирующее

Также называется РД-звеном. Примером физической реализации РД-звена можно считать RC-цепочку, приведенную на рис. 8-3.

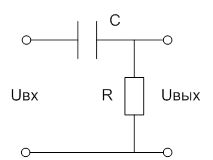
Рис. 3-6. Пример физической реализации РД-звена.

В системе, показанной на рис. 8-3, входным воздействием является входное напряжение, а выходной величиной – выходное напряжение, то есть, напряжение, снимаемое с резистора.

Дифференциальное уравнение РД-звена имеет вид: .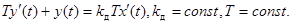

Коэффициент k_д в дифференциальном уравнении РД-звена называется также коэффициентом передачи РД-звена. Необходимо заметить, что это размерная величина, размерность которой представляет собой отношение размерности выходного сигнала, умноженной на время, к размерности входного сигнала. Т – постоянная времени дифференцирования, имеет размерность времени.

Передаточная функция РД-звена имеет вид: .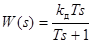

КЧХ РД-звена имеет вид: .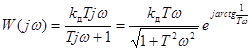

АЧХ РД-звена имеет вид: .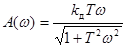

ФЧХ РД-звена имеет вид: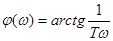

Переходная характеристика РД-звена имеет вид: .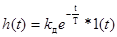

Импульсная переходная характеристика РД-звена: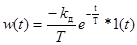

Годограф КЧХ РД-звена приведен на рис. 8-4.

Рис. 3-7. Пример годографа КЧХ РД-звена.

Пример АЧХ РД-звена приведен на рис. 8-5, коэффициент передачи для данного случая равен 5.

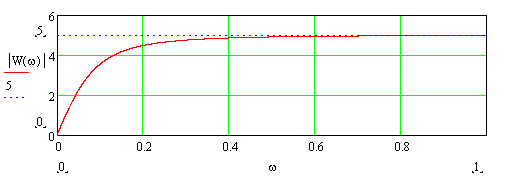
Рис. 3-8. Пример АЧХ РД-звена.

Пример ФЧХ РД-звена приведен на рис. 8-6.

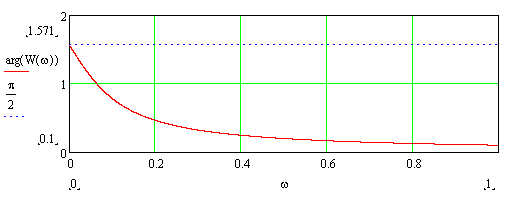
Рис. 3-9. Пример ФЧХ РД-звена.

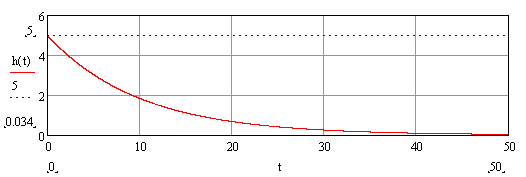
Пример переходной характеристики РД-звена приведен на рис. 8-7. Коэффициент передачи звена в примере равен 5, постоянная времени равна 10.

Рис. 3-10. Пример переходной характеристики РД-звена.

Апериодическое звено

Также называется А-звеном или инерционным звеном первого порядка.

Примером физической реализации А-звена является RC-цепочка, которая рассматривалась в предыдущей лекции при изучении РД-звена, но в этой цепочке нужно поменять местами резистор и конденсатор.

Дифференциальное уравнение А-звена имеет вид: .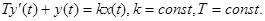

Коэффициент k в дифференциальном уравнении А-звена называется также коэффициентом передачи А-звена. Необходимо заметить, что это размерная величина, размерность которой представляет собой отношение размерности выходного сигнала к размерности входного сигнала. Т – постоянная времени апериодического звена, имеет размерность времени.

Передаточная функция А-звена имеет вид: .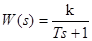

КЧХ А-звена имеет вид: .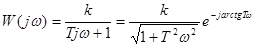

АЧХ А-звена имеет вид: .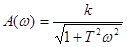

ФЧХ А-звена имеет вид: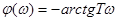

Переходная характеристика А-звена имеет вид: .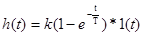

Импульсная переходная характеристика А-звена: .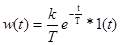

Пример годографа КЧХ А-звена приводится на рис. 9-1. В приведенном примере к=5.

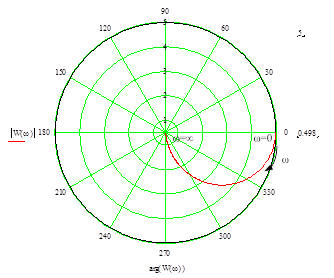
Рис. 3-11. Пример годографа КЧХ А-звена.

Пример фазо-частотной характеристики А-звена приведен на рис. 9-2.

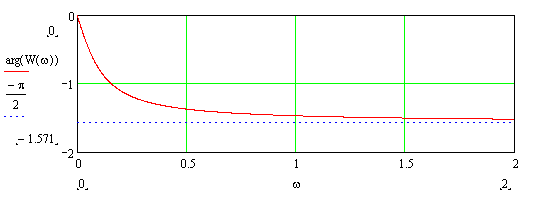
Рис. 3-12. Пример фазо-частотной характеристики А-звена.

Пример амплитудно-частотной характеристки А-звена показан на рис. 9-3. В данном примере к=5.

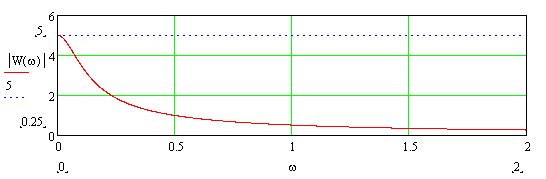
Рис. 3-13. Пример амплитудно-частотной характеристики А-звена.

Пример переходной характеристики А-звена показан на рис. 9-4. В данном примере к=5, Т=10.

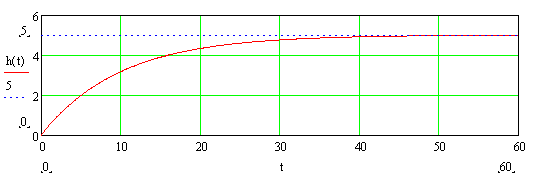
Рис. 3-14. Пример переходной характеристики А-звена.

Пример импульсной переходной характеристики того же А-звена показан на рис. 9-5.

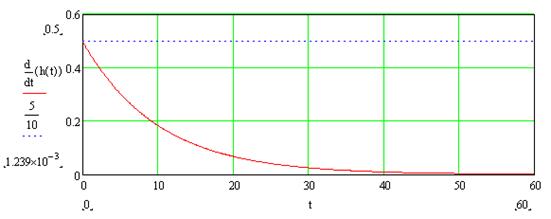
Рис. 3-15. Пример импульсной переходной характеристики А-звена.

Звено запаздывания

Также называется З-звеном. Примером физической реализации данного звена может являться транспортер.

Переходная характеристика З-звена имеет вид: .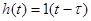

КЧХ З-звена имеет вид: .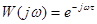

АЧХ З-звена имеет вид: А(ω)=1.

ФЧХ З-звена имеет вид: φ(ω)=-ωτ.

Вид годографа КЧХ З-звена приведен на рис. 9-10.

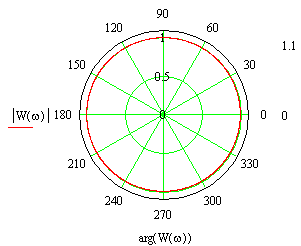
Рис. 3-20. Пример годографа КЧХ звена запаздывания.

Последовательное соединение

Последовательное соединение звеньев показано на рис. 10-1

Рис. 3-21. Последовательное соединение звеньев.

При последовательном соединении звеньев передаточная функция системы представляет собой произведение передаточных функций составляющих:

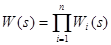. (10-1)

Аналогично можно найти КЧХ данной системы:

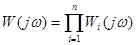. (10-2)

Тогда АЧХ и ФЧХ можно найти, соответственно, по формулам:

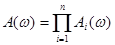(10-3)

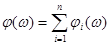(10-4)

В данном случае при построении годографа КЧХ удобнее сначала построить графики АЧХ и ФЧХ, а затем строить годограф. Необходимо так же заметить, что переходную характеристику в данном случае можно найти, например, через интеграл свертки. Перемножать переходные характеристики составляющих ни в коем случае нельзя.

Параллельное соединение

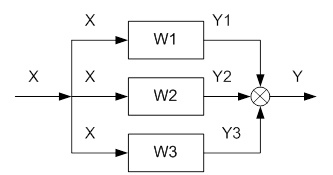
Параллельное соединение звеньев показано на рис. 10-2.

Рис. 3-22. Параллельное соединение звеньев.

Для параллельного соединения звеньев передаточная функция системы ищется по формуле:

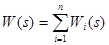(10-5)

Аналогично можно найти КЧХ:

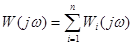(10-6)

При построении годографа КЧХ параллельного соединения звеньев, зная годографы составляющих, складывают векторы на соответствующих частотах по правилу параллелограмма. В данном случае удобнее сначала найти годограф КЧХ и по нему строить графики АЧХ и ФЧХ.

Переходную характеристику всей системы так же можно найти, сложив переходные характеристики составляющих.

Основные понятия имитационного моделирования. Разностные уравнения

Выражение для y(t) не всегда можно найти путем решения дифференциального уравнения или через преобразования Фурье и Лапласа или через интеграл свертки.

Это происходит потому, что не всегда можно получить математическое описание объекта в явном виде и линеаризовать. Кроме того, исследуемый объект может быть подвержен одновременному действию нескольких возмущений, поступающих на различные входы. Возмущения могут быть различного характера, в том числе, случайные.

В описанных случаях можно применять имитационное моделирование, то есть, численное решение дифференциальных уравнений (для дифференциальных уравнений первого порядка – метод Эйлера).

Например, для апериодического звена можно записать:

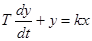; (12-5)

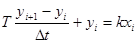. (12-6)

Из последней формулы можно с помощью арифметических преобразований выразить y_i₊₁. Полученная формула носит название рекуррентной и для А-звена имеет вид:

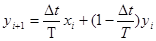. (12-7)

Аналогичные формулы могут быть получены для всех элементарных звеньев. Далее модель объекта может быть "набрана" из элементарных звеньев, как из блоков. Пусть имеется система, показанная на рис. 12-2.

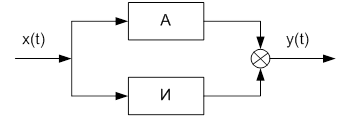
Рис. 12-2. Параллельное соединение А и И-звеньев.

При реализации в программе MathCad формулы для данного случая будут иметь вид:

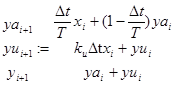. (12-8)

Контрольные вопросы

В чем состоит принцип наложения?

Какая динамическая система называется линейной?

Какие существуют типовые (или тестовые) входные воздействия?

Что называется функцией Хевисайда?

Что называется переходной характеристикой?

Что называется функцией Дирака?

Что называется импульсной переходной характеристикой?

Как можно экспериментально найти переходную/импульсную переходную характеристику?

Как можно представить произвольное входное воздействие в виде последовательности импульсов? В виде последовательности ступенек?

Что называется интегралом свертки?

В чем состоит различие статической и динамической систем?

Запишите формулу прямого и обратного преобразования Лапласа.

Для чего применяется преобразование Лапласа?

Запишите изображение по Лапласу функции Хевисайда, линейной функции, экспоненты.

Каковы свойства преобразования Лапласа?

Как вычислить начальное и конечное значение оригинала, зная изображения?

Что называется передаточной функцией?

Каким образом можно получить передаточную функцию по дифференциальному уравнению системы?

Каким образом можно решить дифференциальное уравнение с помощью преобразования Лапласа?

Запишите дифференциальное уравнение апериодического звена, постройте его характеристики.

Приведите пример технической реализации А-звена.

Какие существуют типовые соединения звеньев?

Как найти передаточную функцию системы, состоящей из последовательно соединенных звеньев, зная передаточные функции составляющих?

Можно ли найти переходную характеристику системы, состоящей из последовательно соединенных звеньев, перемножив переходные характеристики входящих в нее звеньев? Почему?

Как найти АЧХ и ФЧХ системы, состоящей из последовательно соединенных звеньев, зная АЧХ и ФЧХ составляющих?

Как найти передаточную функцию системы, состоящей из параллельно соединенных звеньев, зная передаточную функцию каждого звена?

Как найти переходную характеристику параллельного соединения звеньев, зная переходные характеристики каждого звена?

Какие существуют виды обратной связи?

Как найти передаточную функцию системы с обратной связью, зная передаточные функции составляющих?