Составим дифференциальное уравнение для объекта с сосредоточенными ёмкостями. Уравнения энергетического и материального баланса составляется для каждой ёмкости и представляет собой дифференциальное уравнение первого порядка, если в объекте n ёмкостей, соответственно, будет n уравнений.

Дифференциальное уравнение имеет вид:

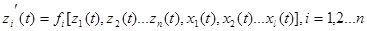;                               (3-1)

где: z_i – переменные состояния системы, характеризующие содержание вещества или энергии в ёмкостях в каждый момент времени t;

x₁… x_l – внешние (входные) воздействия на систему, приводящие к изменению ее состояния.

В общем случае количество переменных состояния и входных воздействий не равны друг другу.

Обычно требуются не переменные состояния, а некоторые другие величины, связанные с переменными состояния некоторой функциональной зависимостью., эти величины называются выходными величинами системы. Зависимость выходных величин от переменных состояния и входных воздействий выражается в виде:

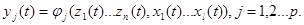;                                            (3-2)

где: y_i – выходные величины системы.

Входные и выходные величины в общем случае не привязаны к входным и выходным потокам вещества или энергии.

Дадим математическое определение динамической системы (такую систему мы в данный момент рассматриваем). Также дадим математическое определение статической системы.

Динамическая система – система, поведение которой описывается дифференциальным уравнением.

Статическая система – система, в дифференциальных уравнениях которой (3-1) производные в левой части равны нулю.

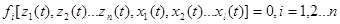                                 (3-3)

Приближенным примером статической системы может служить динамическая система при сравнительно медленном изменении входных воздействий, при этом процесс накопления в ёмкостях вещества или энергии протекает без заметной задержки вслед за изменением входных воздействий.

Система находится в состоянии покоя, если:

- входные воздействия неизменны во времени [ ];

- переменные состояния неизменны во времени [ ].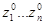

Тогда:

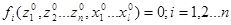.                                                   (3-4)

Рассматриваемые нами системы бывают линейными и нелинейными.

Линейной называется система, все функции ХХХ которой в её дифференциальных уравнениях (3-1) линейны. Если хотя бы одна из упомянутых функций нелинейна, то система называется нелинейной.

Нелинейные системы, в свою очередь, делятся на линеаризуемые и нелинеаризуемые. Нелинейная система называется линеаризуемой, если функции ХХХ можно представить в линейном виде. Если хотя бы одну из этих функций в линейном виде представить нельзя, система называется нелинеаризуемой. Линеаризацией называется замена нелинейной функции приближенной линейной функцией.

В общем случае все системы нелинейные, их стремятся линеаризовать. После линеаризации дифференциальные уравнения (3-1) примут вид:

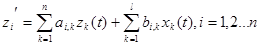                                       (3-5)

Линеаризация всегда сопровождается потерей точности. При линеаризации важно помнить, что устойчивость линеаризованной системы должна отражать устойчивость исходной нелинейной системы.

Преобразование Лапласа

Дифференциальные уравнения можно решать различными способами; рассмотрим методы решения неоднородных линейных дифференциальных уравнений. Их можно решать методом вариации произвольных постоянных или операторным методом (то есть, с помощью преобразования Лапласа). Рассмотрим последний метод.

С помощью преобразования Лапласа каждой функции в пространстве оригиналов ставится в соответствие некая функция в пространстве изображений. Переход от оригинала к изображению выполняется по формуле:

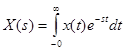,                                                          (3-6)

где: 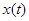- оригинал, ;

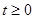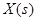 - изображение функции-оригинала.

Переменная s является комплексной и имеет вид 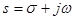. Изображение по Лапласу обозначается:

.                                                           (3-7)

Рассмотрим пример. Пусть 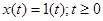 - данная функция называется функцией Хевисайда, она равна нулю при 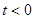и единице во всех остальных случаях, то есть, представляет собой единичную ступеньку, возникающую в момент времени .

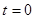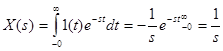.                                           (3-8)

Прочие примеры приведены в учебнике В.Я. Ротача. Изображение основных функций по Лапласу необходимо выучить наизусть.

Свойства преобразования Лапласа

Преобразование Лапласа имеет ряд свойств; ряд свойств приводятся ниже.

1. Линейность.

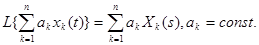                                    (3-9)

1. Изображение производной оригинала выражается формулой:

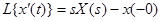.                                              (3-10)

В задачах теории автоматического управления часто 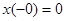, поэтому выражение (4-5) можно переписать следующим образом:

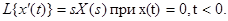                                     (3-11)

Аналогично можно выразить производные более высоких порядков, при 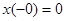 можно записать:

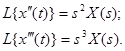                                               (3-13)

1. Начальное значение оригинала при 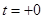выражается формулой:

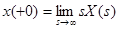.                                               (3-14)

1. Конечное значение оригинала:

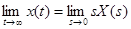.                                              (3-15)

Передаточная функция. Решение дифференциальных уравнений с помощью преобразования Лапласа

Пусть имеется дифференциальное уравнение динамической системы, выведенное на предыдущей лекции:

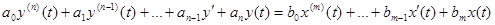.            (3-16)

Пусть входное воздействие 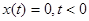, а рассматриваемая система до 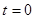находилась в состоянии покоя, то есть, 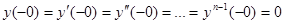. Умножим обе части данного дифференциального уравнения на  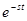и проинтегрируем от -0 до ∞, то есть, выполним преобразование Лапласа. Тогда получим:

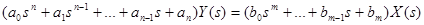                (3-17)

Введем обозначения:

,

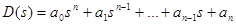.                                        (3-18)

Тогда получим выражение:

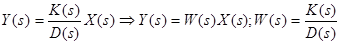,                            (3-19)

где: W( s) – функция комплексного переменного s, называемая передаточная функция системы (ПФ).

Передаточная функция системы - отношение преобразованной по Лапласу выходной величины системы к преобразованному по Лапласу входному воздействию при нулевых начальных условиях.

Передаточная функция представляет собой описание объекта, подобно дифференциальному уравнению, но при этом она не имеет физического смысла.

Передаточную функцию системы можно получить по ее дифференциальному уравнению, для этого:

1. Производные в левой и правой частях заменить на s в степени, равной порядку заменяемой производной;
2. Полином, полученной в правой части –является числителем передаточной функции, а полином в левой части – ее знаменателем.

Знаменатель передаточной функции является характеристическим уравнением системы (ХУ). Корни ХУ называются полюсами ПФ.

С помощью преобразования Лапласа решить ДУ можно следующим образом:

1. Преобразовать по Лапласу входное воздействие: ;

2. По дифференциальному уравнению составить передаточную функцию системы;

3. Записать выражение для изображения выходной величины: ;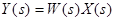

4. Выполнить обратное преобразование Лапласа и получить оригинал выходной величины системы: .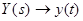

Обратное преобразование Лапласа выполняется по формуле:

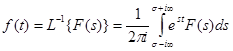;                                               (3-20)

где: σ – действительное число.