Линейные динамические системы имеют два отличительных признака: они описываются ЛДУ, и для них справедлив принцип наложения (суперпозиций).

Принцип суперпозиций заключается в следующем. Если на входе в динамическую систему имеется воздействие, представляющее собой сумму некоторых воздействий ( 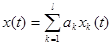), то реакция системы на данное воздействие представляет собой сумму реакций на каждое воздействие ( ).

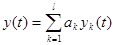Для исследования линейных систем применим не только метод дифференциальных уравнений, но и другие методы. Например, свойства этих систем можно описывать с помощью динамических характеристик.

Динамическая характеристика – это характеристика, определяющая реакцию системы на некоторые типовые входные воздействия (их также называют тестовыми воздействиями).

Подбор тестовых воздействий осуществляется таким образом, чтобы любое возможное в процессе эксплуатации воздействие на систему можно было представить взвешенной суммой типовых воздействий. Таким образом, используя принцип наложения можно определить реакцию системы на любое воздействие.

Типовые воздействия

Существует несколько видов типовых воздействий.

1. Единичное ступенчатое воздействие (функция Хевисайда);
2. Дельта-функция, функция Дирака;
3. Гармонические колебания единичной амплитуды.

Переходная характеристика – это реакция объекта/системы на функцию Хевисайда.

Импульсная переходная характеристика – реакция объекта/системы на дельта-функцию.

Кривая разгона – реакция объекта/системы на ступенчатое воздействие произвольной величины.

Необходимо иметь в виду следующее. Пусть функция f(t) определена на (-∞,∞), тогда:

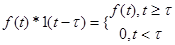;                                                   (3-21)

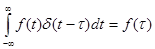.                                                   (3-22)

Интеграл свертки

Покажем, что имею любую из описанных динамических характеристик (переходную или импульсную характеристику), можно вычислить реакцию линейной системы на входное воздействие произвольного вида.

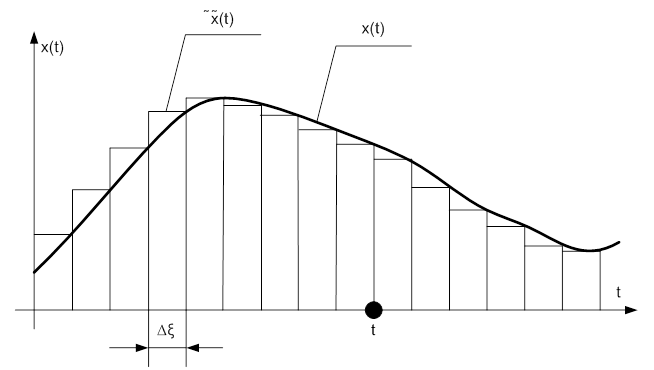
Пусть на входе в динамическую систему имеется произвольное входное воздействие x(t). График зависимости от времени входного воздействия приведен на рис. 5-1.

Рис. 3-1. График зависимости от времени входного воздействия.

Найдем значение выхода системы в произвольный момент времени t (этот момент произволен, но зафиксирован).

Разобьем ось времени на небольшие отрезки длительностью Δξ, далее построим новую функцию времени 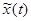, совпадающую с исходной в точках разбиения и остающуюся постоянной в промежутках между ними. Можно записать, что

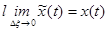.                                                             (3-23)

При этом 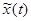 - это последовательность прямоугольных импульсов длительностью Δξ, таким образом, реакцию линейной системы на  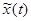можно вычислить как сумму реакций на каждый импульс, взятый отдельно.

Пусть 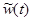- реакция системы на прямоугольный импульс длительностью Δξ и амплитудой 1/Δξ (то есть, на импульс единичной площади). Тогда, если импульсы имеют амплитуду А, то можно записать .

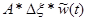Тогда реакция системы (у(t)) в фиксированный момент времени t на последовательность импульсов ( 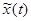) можно вычислить по формуле (принцип наложения):

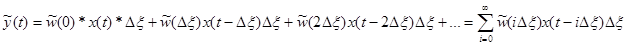. (3-24)

Точное решение можно найти при 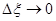, тогда 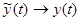, , 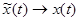, 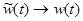а сумма переходит в интеграл. Таким образом, можно записать:

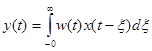.                                                  (3-25)

ИПХ должна удовлетворять условию физической реализуемости, то есть, равняться нулю при t<0, поэтому без потери смысла можно записать выражение 5-5 следующим образом:

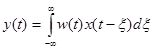.                                                  (3-26)

Если воздействие внезапно приложено в нулевой момент времени, и начальные условия нулевые, то можно записать:

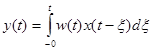.                                                  (3-27)

Выражение (5-7) называется интеграл свертки.

Если входное воздействие представляет собой функцию Хевисайда, то можно получить выражение для переходной характеристики:

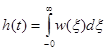.                                                  (3-28)

Необходимо заметить, что ИПХ – это производная от ПХ.

Из интеграла свертки следует, что выходная величина динамической системы в некоторый момент времени зависит не только от входного воздействия в этот момент времени, но и в предыдущие моменты времени. То есть, динамическая система обладает «памятью» на входные воздействия, статическая – не обладает.

Спектральное представление сигналов. Преобразование Фурье

Любую функцию времени можно представить в виде суммы соответствующим образом подобранных гармонических колебаний вида:

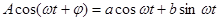                                                (3-29)

где: 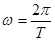 - угловая частота колебаний;

Т – период колебаний;

А - амплитуда колебаний;

φ – начальная фаза колебаний.

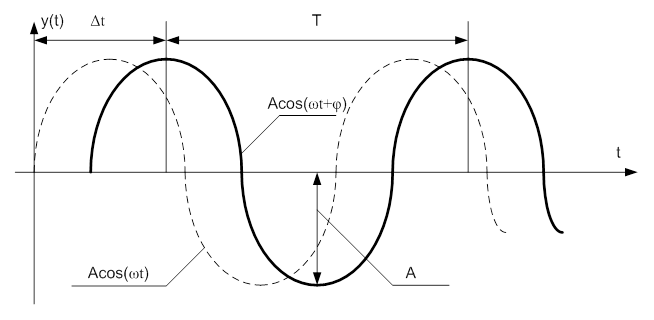
Графики колебаний показаны на рис. 6-1.

Рис. 3-2. Колебания на входе и на выходе в систему.

Можно записать, что: 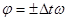, при этом  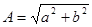и

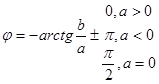                                                           (3-30)

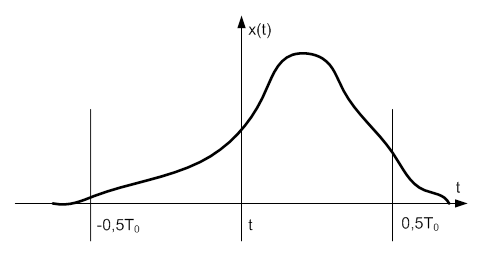
Пусть имеется функция произвольного вида x(t), которую нужно представить в виде суммы гармоник. График функции показан на рис. 6-2.

Рис. 3-3. График произвольной функции x(t).

Выберем период Т₀ и построим новую функцию 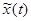, имеющую указанный период и совпадающую с исходной на отрезке 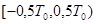. Если функция  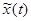удовлетворяет условию 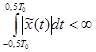, то её можно представить рядом Фурье, то есть суммой гармоник с частотами ω₀, 2ω₀, 3ω₀ (то есть, с частотами, кратными 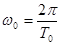). Тогда функция  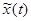будет иметь вид:

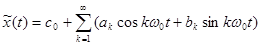.                                           (3-31)

Формула 6-3 представляет собой ряд Фурье, коэффициенты этого ряда определяются формулами:

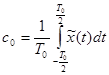,                                                           (3-32)

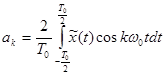,                                                   (3-33)

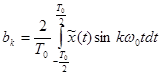.                                                     (3-34)

С учетом формул (6-4)-(6-6) ряд Фурье можно записать в виде:

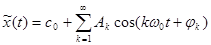.                                                (3-35)

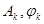 - амплитуда и начальная фаза k-ой гармоники.

Совокупность чисел 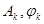 называется амплитудным и фазовым спектрами функции 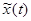, где k – целое положительное число. Разложение функции  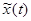в ряд Фурье называется спектральным разложением .

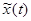С учетом известной формулы Эйлера можно получить

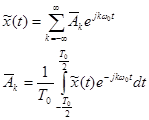;                                                           (3-36)

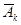 - комплексное число, полностью определяющее к-ую гармонику разложения. Связь  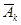с амплитудой и начальной фазой к-ой гармоники определяется формулой:

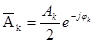.                                                         (3-37)

Чтобы получить разложение на гармоники исходной непериодической функции нужно устремить принятый период Т₀ к бесконечности. При этом аплитуды гармоник будут стремиться к нулю (см. формулы 6-7 и 6-8), поэтому необходимо ввести новые комплексные коэффициенты разложения:

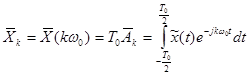.                                    (3-38)

При этом изменится вид (6-7):

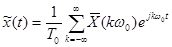.                                                 (3-39)

С учетом того, что разность частот соседних гармоник равна ω₀, получим:

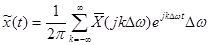.                                             (3-40)

При стремлении Т₀ к бесконечности в итоге получим:

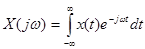                                                    (3-41)

Формула (6-12) представляет собой прямое преобразование Фурье. Нижеследующая формула (6-13) представляет собой обратное преобразование Фурье:

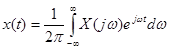.                                                (3-42)

Прямое и обратное преобразования Фурье обозначаются соответственно:

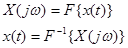.                                                      (3-43)

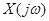 - изображение исходной функции по Фурье, комплексная функция частоты. Модуль изображения по Фурье от x(t) является распределением по частотам амплитуд гармоник в разложении x(t). Изображение по Фурье от x(t) называется комплексной спектральной плотностью x( t).