Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Комплексная оценка экономической деятельности представляет ее характеристику, полученную в результате комплексного исследования, т. е. одновременного и согласованного изучения совокупности показателей, отражающих хозяйственные процессы.

Основная задача проведения комплексного анализа деятельности предприятия заключается в выборе системы индикаторов и методического инструментария.

Процесс проведения комплексной оценки явлений можно разделить на следующие этапы.

- постановка цели и задач исследования

- выбор исходной системы показателей

- организация сбора исходной информации

- расчет и оценка полученных данных

- выбор и расчет комплексных сравнительных оценок

- выбор адекватных моделей реальной экономической деятельности

- использование полученных данных

Для получения обобщающих комплексных оценок можно применять различные методы введения различных показателей в единый интегральный показатель, сведение ряда показателей в единый интегральный показатель позволяет определить, какие произошли отличия по сравнению с базисным периодом.

Слово «рейтинг» обозначает выстраивание некоторых единиц в определенном порядке, в соответствии с заранее установленными правилами и категориями. В экономическом анализе проведение рейтингов позволяет расположить предприятия в определенном порядке, в результате выбранных критериев оценки. Сравнение предприятия с родственными ему по отраслевой принадлежности или объемам деятельности предприятиями дает возможность определить его место среди конкурентов.

Построение рейтингов может осуществляться как на основе абсолютных, так и относительных показателях, однако следует отметить, что предпочтение следует отдавать относительным так как они позволяют проводить сравнения различных хозяйствующих субъектов.

Для интегральных показателей можно использовать следующие методы:

- метод сумм

- метод геометрической средней

- метод суммы мест

- метод расстояний

Оценка интегрального показателя с помощью метода сумм, осуществляется с помощью простого суммирования по формуле:

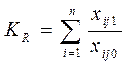 , где x_ij1 и x_ij0 - соответственно фактическое и базисное значение i-го показателя на j-м производственном объекте.

Метод геометрической средней предполагает расчет коэффициентов для оцениваемых показателей находящихся в пределах 0£a_ij£1. За 1 принимается значение наивысшего уровня показателя.

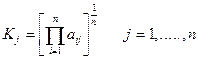
Метод суммы мест предполагает предварительное ранжирование по выбранным показателям.

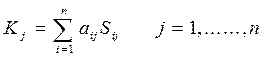
Основой метода расстояний является учет близости объектов по сравниваемым показателям к объекту-эталону. За эталон принимают условный объект с наилучшими показателями.

Исходные показатели стандартизируются по формуле:

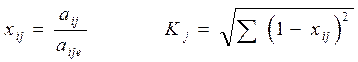
В основе расчета итогового показателя рейтинговой оценки лежит сравнение предприятий по каждому выбранному для рейтинга показателю с условным эталонным предприятием, имеющим наилучшие результаты по всем сравниваемым показателям. Таким образом, базой отсчета для получения рейтинговой оценки состояния дел предприятия являются не субъективные предположения экспертов, а сложившиеся в реальной рыночной конкуренции наиболее высокие результаты из всей совокупности сравниваемых объектов. Эталоном сравнения как бы является самый удачливый конкурент, у которого все показатели наилучшие.

Такой подход соответствует практике рыночной конкуренции, где каждый самостоятельный товаропроизводитель стремится к тому, чтобы по всем показателям деятельности выглядеть лучше своего конкурента.

Если субъектов рыночных отношений интересует только вполне определенные объекты хозяйственной деятельности (например, показатели работы только кондитерских фабрик или предприятий химической промышленности, или машиностроительных заводов и т.д.), то эталонное предприятие формируется из совокупности однотипных объектов. Однако, в большинстве случаев эталонное предприятие может формироваться из показателей работы объектов, принадлежащих различным отраслям деятельности. Это не является препятствием применению метода оценки, потому, что показатели сопоставимы и для разнородных объектов хозяйствования.

В общем виде алгоритм сравнительной рейтинговой оценки предприятия может быть представлен в виде последовательности следующих действий:

1. Исходные данные представляются в виде матрицы (a_ij), то есть таблицы, где по строкам записаны номера показателей (i = 1,2,3,...,n), а по столбцам - номера предприятий (j = 1,2,3,...,m).

2. По каждому показателю находится максимальное значение и заносится в столбец условного эталонного предприятия (m+1).

3. Исходные показатели матрицы a_ij стандартизируются в отношении соответствующего показателя эталонного предприятия по формуле:

x_ij = 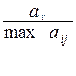, где

x_ij - стандартизированные показатели состояния j-го предприятия.

 

4. Для каждого анализируемого предприятия значение его рейтинговой оценки определяется по формуле:

R_j = 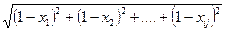;где

R_j - рейтинговая оценка для j-го предприятия;

x _{1 j} , x _{2 j} , ... x_nj - стандартизированные показатели j-го анализируемого предприятия.

5. Предприятия упорядочиваются (ранжируются) в порядке убывания рейтинговой оценки.

Наивысший рейтинг имеет предприятие с минимальным значением R. Для применения данного алгоритма на практике никаких ограничений количества сравниваемых показателей и предприятий не предусмотрено.

Изложенный алгоритм получения рейтинговой оценки может применяться для сравнения предприятий на определенное состояние или в динамике.

Пример

Имеются данные показателей финансовой устойчивости по 10 предприятиям города. С помощью различных методов комплексной рейтинговой оценки составим их рейтинг.

1. Определим рейтинг с помощью метода сумм

Таблица 4.28

Показатели финансовой устойчивости по промышленным предприятиям города

Предприятия

Коэффициенты

Сумма коэффициентов

(1+2+3+4)=5

Рейтинг

финансовой устойчивости финансирования инвестирования маневренности   1 2 3 4 5

6

1. 0,42 0,72 1,21 0,17 2,52

10

2. 0,6 1,53 1,23 0,19 3,55

8

3. 0,81 4,31 1,21 0,17 6,50

3

4. 0,44 0,8 1,32 0,24 2,80

9

5. 0,7 2,34 1,25 0,2 4,49

7

6. 0,93 14,27 1,32 0,24 16,76

1

7. 0,89 8,36 1,21 0,17 10,63

2

8. 0,78 3,61 1,29 0,22 5,90

4

9. 0,75 3,04 1,26 0,21 5,26

6

10. 0,78 3,56 1,29 0,23 5,86

5

               

 

Покажем расчет рейтинга на примере предприятия №1:

R₁=0,42+0,72+1,21+0,17=2,52

Среди выбранных предприятий сумма оказалась наименьшей, поэтому предприятию присваивается 10 место.

 

 

2. Определим рейтинг с помощью метода геометрической средней

Для этого определим стандартизированные показатели, присвоив наилучшему значению показателя единицу. Лучшее значение коэффициента:

финансовой устойчивости                  0,93

финансирования                                 14,27

инвестирования                                   1,32

маневренности                                  0,24

Таблица 4.29.

Расчет рейтинга по показателям финансовой устойчивости с помощью метода геометрической средней

Предприятия	Коэффициенты				Cтандартизированные показатели				Интегральный показатель	Рейтинг
	финансовой устойчивости	финансирования	инвестирования	маневренности	а	b	c	d
1.	0,42	0,72	1,21	0,17	0,451	0,050	0,916	0,708	0,350	10
2.	0,6	1,53	1,23	0,19	0,645	0,107	0,931	0,791	0,475	8
3.	0,81	4,31	1,21	0,17	0,871	0,302	0,916	0,708	0,643	5
4.	0,44	0,8	1,32	0,24	0,473	0,056	1,000	1,000	0,405	9
5.	0,7	2,34	1,25	0,2	0,752	0,164	0,946	0,833	0,560	7
6.	0,93	14,27	1,32	0,24	1,000	1,000	1,000	1,000	1,000	1
7.	0,89	8,36	1,21	0,17	0,957	0,585	0,916	0,708	0,776	2
8.	0,78	3,61	1,29	0,22	0,838	0,253	0,977	0,916	0,660	4
9.	0,75	3,04	1,26	0,21	0,806	0,213	0,954	0,875	0,616	6
10.	0,78	3,56	1,29	0,23	0,838	0,249	0,977	0,958	0,665	3

 

Покажем расчет рейтинга на примере предприятия №1

а₁= 0,42/0,93=0,451                   b₁= 0,72/14,27=0,05

c₁= 1.21/1,32=0,916                   d₁= 0,17/0,24=0,708

Далее согласно формулы находим произведение в степени ¼ стандартизированных показателей. Таким образом, рейтинг предприятия №1 равен:

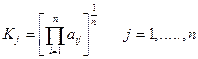
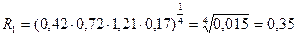
Среди исследуемых предприятий это наименьший результат, поэтому присваивается 10 место

 

3. Метод суммы мест предполагает предварительное ранжирование по выбранным показателям, затем суммирование и определение рейтинга.

Таблица 4.30.

Расчет рейтинга по показателям финансовой устойчивости с помощью метода суммы мест

Предприятия	Коэффициенты				Ранжирование показателей				Сумма мест	Рейтинг
	финансовой устойчивости	финансирования	инвестирования	маневренности	финансовой устойчивости	финансирования	инвестирования	маневренности
1.	0,42	0,72	1,21	0,17	10	10	8	8	36	10
2.	0,6	1,53	1,23	0,19	8	8	7	7	30	9
3.	0,81	4,31	1,21	0,17	3	3	1	8	15	2
4.	0,44	0,8	1,32	0,24	9	9	8	1	27	8
5.	0,7	2,34	1,25	0,2	7	7	6	6	26	7
6.	0,93	14,27	1,32	0,24	1	1	1	1	4	1
7.	0,89	8,36	1,21	0,17	2	2	8	8	20	2
8.	0,78	3,61	1,29	0,22	4	4	3	4	15	2
9.	0,75	3,04	1,26	0,21	6	6	5	5	22	6
10.	0,78	3,56	1,29	0,23	4	5	3	3	15	2

 

Покажем расчет рейтинга на примере предприятия №10

Сумма баллов по выбранным показателям составляет:

10+10+8+8=36

При использовании данного метода 1 место присваивается предприятию набравшему минимальную сумму мест. В нашем случае набранная сумма мест является максимальной, поэтому предприятие №1 в рейтинге занимает 10 место.

4. Определим рейтинг с помощью метода расстояний.  

Стандартизированные показали нами были рассчитаны при определении рейтинга по средней геометрической, поэтому далее рейтинг для каждого предприятия определим по формуле:

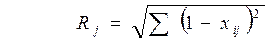
Таблица 4.31.

Расчет рейтинга с помощью метода расстояний

Предприятия	Коэффициенты				Cтандартизированные показатели				Интегральный показатель	Рейтинг
	финансовой устойчивости	финансирования	инвестирования	маневренности	а	b	c	d
1.	0,42	0,72	1,21	0,17	0,451	0,050	0,916	0,708	1,138	10
2.	0,6	1,53	1,23	0,19	0,645	0,107	0,931	0,791	0,985	8
3.	0,81	4,31	1,21	0,17	0,871	0,302	0,916	0,708	0,772	5
4.	0,44	0,8	1,32	0,24	0,473	0,056	1,000	1,000	1,081	9
5.	0,7	2,34	1,25	0,2	0,752	0,164	0,946	0,833	0,889	7
6.	0,93	14,27	1,32	0,24	1,000	1,000	1,000	1,000	0,000	1
7.	0,89	8,36	1,21	0,17	0,957	0,585	0,916	0,708	0,515	2
8.	0,78	3,61	1,29	0,22	0,838	0,253	0,977	0,916	0,770	4
9.	0,75	3,04	1,26	0,21	0,806	0,213	0,954	0,875	0,821	6
10.	0,78	3,56	1,29	0,23	0,838	0,249	0,977	0,958	0,769	3

 

Так для предприятия №1 рейтинг составит:

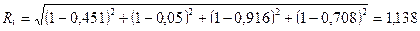
Максимальное значение интегрального показателя свидетельствует о последнем месте в рейтинге среди исследуемых предприятий по выбранным показателям.

Подведем итоги и составим таблицу расчета рейтинга предприятий по показателям финансовой устойчивости, с помощью различных методов комплексной оценки.

Данные таблицы 4.32. показывают, что за исключением метода суммы мест, все остальные способы дали один и тот же вариант распределения рейтинга среди 10 предприятий города.

Таблица 4.32.

Итоги расчета рейтинга по показателям финансовой устойчивости с помощью методов комплексной оценки

Предприятия	Коэффициенты				МЕСТО В РЕЙТИНГЕ
	финансовой устойчивости	финансирования	инвестирования	маневренности	Метод суммирования	Метод геометрической средней	Метод суммы мест	Метод расстояний
1.	0,42	0,72	1,21	0,17	10	10	10	10
2.	0,6	1,53	1,23	0,19	8	8	9	8
3.	0,81	4,31	1,21	0,17	5	5	2	5
4.	0,44	0,8	1,32	0,24	9	9	8	9
5.	0,7	2,34	1,25	0,2	7	7	7	7
6.	0,93	14,27	1,32	0,24	1	1	1	1
7.	0,89	8,36	1,21	0,17	2	2	2	2
8.	0,78	3,61	1,29	0,22	4	4	2	4
9.	0,75	3,04	1,26	0,21	6	6	6	6
10.	0,78	3,56	1,29	0,23	3	3	2	3