Математическое моделирование экономических явлений и процессов дает возможность получить четкое представление об исследуемом объекте, охарактеризовать и количественно описать его внутреннюю структуру и внешние связи. Содержание метода моделирования составляют конструирование модели на основе предварительного изучения объекта и выделения его существенных характеристик, экспериментальный или теоретический анализ модели, сопоставление результатов с данными об объекте, корректировка модели. На практике постоянно встречаются такие ситуации, когда достичь какого-то результата можно не одним, а многими различными способами. Естественно, что когда решений много, ищется в каком-то случае наилучшее. Математически это сводится к нахождению наибольшего или наименьшего значения некоторой функции:
f(x) ® max (min) хÎ Х
5.2.1. Методы линейного программирования
Методы линейного программирования оформились как отдельный раздел прикладной математики в 40-х – 50-х годах ХХ века, когда выяснилось, что целый ряд задач из сферы планирования и управления может быть сформулирован в виде задач линейного программирования. Эксперты считают, что в настоящее время примерно 80-85% всех решаемых на практике задач оптимизации относятся к задачам линейного программирования. Решение таких задач сводится к нахождению крайних значений (максимума и минимума) некоторых функций переменных величин.
С помощью этого метода в промышленном производстве, например, исчисляется оптимальная общая производительность машин, агрегатов, поточных линий (при заданном ассортименте продукции и иных заданных величинах), решается задача рационального раскроя материалов (с оптимальным выходом заготовок). В сельском хозяйстве он используется для определения минимальной стоимости кормовых рационов при заданном количестве кормов (по видам и содержащимся в них питательным веществам). Задача о смесях может найти применение и в литейном производстве (состав металлургической шихты). Этим же методом решаются транспортная задача, задача рационального прикрепления предприятий-потребителей к предприятиям-производителям.
Все экономические задачи, решаемые с применением линейного программирования, отличаются альтернативностью решения и определенными ограничивающими условиями. Для решения таких задач разработаны эффективные методы, один из которых (симплекс-метод) мы рассмотрим на практическом занятии.
5.2.2. Теория очередей
Основы знаний об очередях, иногда называемые теорией очередей или теорией массового обслуживания, составляют важную часть теории управления производством. Анализ очередей в терминах длины очередей, среднего времени ожидания и других факторов помогает нам лучше понять системы обслуживания.
Менеджер оценивает изменения, возникающие в затратах, связанных с обеспечением хорошего обслуживания, и в затратах, связанных с ожиданием в очереди клиента или машины. Он может предложить увеличить время ожидания, если соблюдается баланс между количеством продаж и затратами на обслуживание покупателей. Его задача – организовать такое обслуживание, чтобы покупатель не ушел без покупки и, если купил то не потерял бы охоту вернуться еще раз.
Характеристика систем массового обслуживания. Рассмотрим три элемента систем массового обслуживания: появление заявок на входе в систему; порядок прохождения очереди, или собственно система обслуживания; средства обслуживания.
Характеристика входа. Входной источник, который генерирует поступление заявок в систему обслуживания, имеет три основные характеристики: число заявок на входе, режим поступления заявок в систему обслуживания и поведение клиентов.
Число заявок на входе. Число заявок (размер популяции) может считаться либо неопределенным (бесконечным), либо ограниченным (конечным). Если число клиентов, поступивших на вход от начала до любого заданного момента времени, является лишь малой частью потенциально возможного их числа, популяция на входе рассматривается как неограниченная, или бесконечная. На практике примерами неограниченных популяций могут служить автомобили, проходящие через пропускные пункты на скоростных дорогах, покупатели в супермаркете. Многие модели очередей рассматривают на входе такие неограниченные популяции.
Режим поступления в систему. Клиенты приходят в систему обслуживания в соответствии с определенным графиком (например, один пациент каждые пятнадцать минут, один студент на экзамене каждые полчаса) или появляются случайным образом.
Поступления клиентов считаются случайными, если они независимы друг от друга и точно не предсказуемы. Часто в задачах массового обслуживания число поступлений в единицу времени может быть оценено с помощью распределения вероятностей, известного как пуассоновское. При заданном темпе поступления (например, два клиента в час или четыре грузовика в минуту) дискретное распределение Пуассона описывается следующей формулой
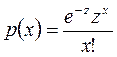для х=0,1,...4, где
р(х) – вероятность х заявок;
х – число заявок в единицу времени;
z – средний темп поступления заявок;
е = 2,7183 (основание натурального логарифма).
Соответствующие вероятности нетрудно определить с помощью таблицы пуассоновского распределения. Если средний темп поступления заявок два клиента в час, то вероятность того, что в течение часа не будет ни одной заявки, равна 0,13, вероятность появления одного клиента – около 0,27, вероятность поступления двух заявок – около 0,27, три клиента в течение часа могут с вероятностью 0,18, четыре – с вероятностью около 0,09 и т. д. Вероятность того, что будет 9 или более заявок, близка к нулю. Вероятность появления заявок, близка к нулю. Вероятности появления клиентов, разумеется, не всегда подчиняются пуассоновскому распределению (они могут иметь какое-то другое распределение), и для того, чтобы убедиться, что пуассоновское распределение может служить хорошей аппроксимацией, следует проводить предварительные исследования.
Поведение клиентов. Большинство моделей очередей основывается на предположении, что каждый появляющийся клиент (человек или машина), вставший в очередь, ждет до тех пор, пока он не будет обслужен, и не переходит из одной очереди в другую. Жизнь значительно сложнее. На практике клиенты могут покинуть очередь потому, что она оказалась слишком длинной. Может возникнуть и другая ситуация – клиенты дожидаются своей очереди, но по каким - то причинам уходят не обслуженными. Эти случаи также являются предметом теории массового обслуживания, однако здесь не рассматриваются.
Характеристики очереди. Очередь является вторым компонентом теории массового обслуживания. Длина очереди может быть либо ограниченной, либо неограниченной. Очередь ограничена, если она по каким-либо причинам (например, из-за физических ограничений) не может увеличиваться до бесконечности. Это может быть, например, очередь в небольшую парикмахерскую, которая имеет ограниченное число мест для ожидания.
Рассматриваемые в данном разделе модели массового обслуживания исходят из предположения неограниченности длины очереди. Длина очереди не ограничена, если она может включать в себя сколько угодно клиентов. Например, очередь автомобилей на бензоколонке.
Вторая характеристика очередей – дисциплина очереди. Эта характеристика связана с правилом, в соответствии с которым обслуживаются клиенты. Большинство систем используют правило: первым пришел – первым ушел. В некоторых случаях, например в приемном покое больницы, в дополнение к этому правилу могут устанавливаться различные приоритеты. Пациент с инфарктом в критическом состоянии будет иметь приоритет в обслуживании по сравнению с пациентом, сломавшим палец. Порядок пуска компьютерных программ – другой пример установления приоритетов в обслуживании.
Характеристики средств обслуживания. Третий компонент систем обслуживания – средства обслуживания. Наибольший интерес представляют следующие их свойства: 1) конфигурация системы обслуживания; 2) временной режим обслуживания.
Основные конфигурации систем массового обслуживания. Системы обслуживания часто классифицируются по числу каналов обслуживания (например, по числу парикмахеров в парикмахерской) и по числу фаз обслуживания (этапов обслуживания одного клиента). Примером одноканальной системы обслуживания могут служить банк, в котором открыто одно окошко для обслуживания клиентов, или ресторан, обслуживающий клиентов в автомобилях. Если же в банке открыто несколько окошек для обслуживания и клиент ожидает в общей очереди, какое из них освободится первым, то мы имеем дело с многоканальной системой обслуживания. Большинство банков, так же как и почтовые отделения и авиакассы, сейчас являются многоканальными системами обслуживания.
Однофазными являются такие системы обслуживания, в которых клиент обслуживается в одном пункте (на одном рабочем месте) и затем покидает систему. Ресторан для обслуживания автомобилистов, в котором официант получает деньги и приносит заказ в автомобиль, является примером однофазовой системы. Тоже можно сказать и об агентстве, выдающем лицензии на вождение, где агент проводит тестирование и выдает лицензию.
Одноканальная однофазовая система
Заявки
Одноканальная двухфазовая система
Заявки
Трехканальная однофазовая система
Заявки
Двухканальная двухфазовая система
Заявки
Однако, если в ресторане нужно сделать заказ в одном месте, оплатить его в другом и получить пищу в третьем, то мы имеем дело в многофазовой системой обслуживания. Если агентство по выдаче лицензий на вождение достаточно большое, то можно подождать в очереди для того, чтобы заполнить заявление, затем в другом месте пройти профессиональный тест и уже затем (третье место обслуживания) оплатить услуги и получить лицензию.
Распределение времени обслуживания. Режим обслуживания, так же как и режим поступления заявок, может быть либо постоянным, либо случайным. Если время обслуживания постоянно, то независимо от клиента требуется одинаковое время для обслуживания, например автомобиля. Такая ситуация может наблюдаться на автоматической мойке машин. Однако более часто встречаются ситуации, когда время обслуживания имеет случайное распределение. Во многих случаях можно предположить, что время обслуживания подчиняется экспоненциальному распределению. это предположение удобно, так же как и предположение о пуассоновском распределении числа поступающих заявок.
Параметры для оценки очередей. Модели очередей помогают менеджеру принять решения, увязывающие затраты на обслуживание с затратами, связанными с ожиданием. Наиболее часто при стоимостной оценке систем массового обслуживания используются следующие параметры:
1) среднее время, которое клиент проводит в очереди;
2) средняя длина очереди;
3) среднее время, которое клиент проводит в системе обслуживания (время ожидания плюс время обслуживания);
4) среднее число клиентов в системе обслуживания;
5) вероятность того, что система обслуживания окажется не занятой;
6) параметр занятости системы;
7) вероятность определенного числа клиентов в системе.
Модели систем массового обслуживания
В управлении производством можно использовать различные модели систем массового обслуживания. Опишем четыре наиболее часто встречающиеся в практике модели. Их характеристики даны в таблице 6.6
Все четыре модели имеют следующие общие характеристики:
1) пуассоновское распределение заявок;
2) правило - FiFo (первым пришел - первым ушел);
3) единственная фаза обслуживания.
Модель А: модель одноканальной системы массового обслуживания с пуассоновским входным потоком заявок и экспоненциальным временем обслуживания.
Наиболее часто встречаются задачи массового обслуживания с единственным каналом. В этом случае клиенты формируют единственную очередь, которая обслуживается одним рабочим местом. Предположим, что для систем этого типа выполняются следующие условия.
Заявки обслуживаются по принципу FIFO.
Среднее число заявок поступающих в единицу времени неизменно, хотя и является случайным процессом.
Темп обслуживания выше темпа поступления заявок.
Средний темп обслуживания известен, хотя время затрачиваемое на обслуживание клиентов различно и описывается экспоненциальным распределением вероятностей.
Таблица 6.6.
Модели систем массового обслуживания
| Модель | Название | Пример | Число каналов | Число фаз | Темп поступ-ления заявок | Темп обслу-живания | Число клиен-тов | Порядок прохож-дения очереди |
| А B C D | Простая система (М/М/I) Многока-нальная (М/М/S) Равномер. обслуживание (M/D/I) Огранич. популяция | Справочное бюро магазина Кассы аэрофлота Автоматическая автомойка Самолеты маленькой авиакомпа-нии | Один Несколь-ко Один Один | Одна Одна Одна Одна | Пуассо-новское Пуассо-новское Пуассо-новское Пуассо-новское | Экспоненциальный Экспоненциальный Экспоненциальный Экспоненциальный | Неограниченное Неограниченное Неограниченное Неограниченное | FiFo FiFo FiFo FiFo |
Формулы для описания модели А:
Число заявок в единицу времени: z
Число клиентов, обслуживаемых в единицу времени: b
Среднее число клиентов в системе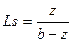 
Среднее время обслуживания одного клиента в системе: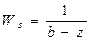 
(время ожидания плюс время обслуживания).
Среднее число клиентов в очереди: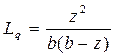 
Среднее время ожидания клиента в очереди: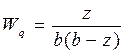 
Параметр загруженности системы: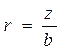 
Вероятность отсутствия заявок в системе: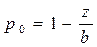 
Вероятность более чем k заявок в системе: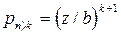 
(n - число заявок в системе).
Модель В: многоканальная система обслуживания
В многоканальной системе для обслуживания клиентов открыты два и более каналов. Предполагается, что клиенты ожидают в общей очереди и обращаются в первый освободившийся канал обслуживания. Пример такой многоканальной однофазовой системы можно увидеть в телефон-автоматах, где клиент подходит к освободившемся телефонным аппаратам. В многоканальной системе поток заявок подчиняется пуассоновскому распределению, а время обслуживания экспоненциальному. Для расчета параметров данной системы целесообразно использовать компьютерное программное обеспечение.
Модель С: модель с постоянным временем обслуживания.
Некоторые системы имеют постоянное, а не экспоненциальное время обслуживания, тогда формулы расчета будут выглядеть следующим образом:
Средняя длина очереди: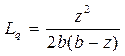 
Среднее время ожидания в очереди: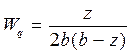 
Среднее число клиентов в системе: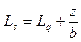 
Среднее время ожидания в очереди: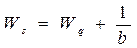 
Модель Д: модель с ограниченной популяцией
Если число потенциальных клиентов системы обслуживания ограничено, в данном случае, чем длиннее очередь на обслуживание, тем ниже темп поступления новых заявок. Расчеты в данной модели достаточно сложны и требуют специального программного обеспечения.
5.2.3. Модели сетевой оптимизации
В математически формализованной системе анализа, планирования и управления особое место занимают сетевые графики. Они позволяют выделить из всего комплекса работ наиболее важные, лежащие на критическом пути, и сосредоточить на них основные ресурсы предприятий, устанавливать взаимосвязь между различными специализированными организациями и координировать их работу. Коммуникационная сеть минимальной длины, или дерево кратчайших расстояний, — это совокупность дуг сети, имеющая минимальную суммарную длину и обеспечивающая достижение всех узлов сети.
5.2.4. Теория игр
Теория игр исследует оптимальные стратегии, связанные с выбором наивыгоднейших производственных решений системы научных и хозяйственных экспериментов, с организацией статистического контроля, хозяйственных взаимоотношений между предприятиями промышленности и других отраслей. Решение подобных задач требует определенности в формировании их условий: установление порядка проведения и правил игры. Для решения задач применяются алгебраические методы, основанные на системе линейных уравнений и неравенств, интеграционные методы, а также сведения, задачи к некоторой системе дифференциальных уравнений.
На промышленных предприятиях теория игр может использоваться для выбора оптимальных решений, например при создании рациональных запасов сырья, материалов, полуфабрикатов, в вопросах качества продукции и других экономических ситуациях. В первом случае противоборствуют две тенденции: увеличения запасов, в том числе и страховых, гарантирующих бесперебойную работу производства; сокращения запасов, обеспечивающих минимизацию затрат на их хранение; во втором — стремления к выпуску большего количества продукции, ведущего к снижению трудовых затрат; к повышению качества, сопровождающемуся часто уменьшением количества изделий и, следовательно, возрастанием трудовых затрат. В машиностроительном производстве противоборствующими направлениями являются стремление к максимальной экономии металла в конструкциях, с одной стороны, и обеспечение необходимой прочности конструкций — с другой.
В сельском хозяйстве теория игр может применяться при решении экономических задач, в которых оппозиционной силой выступает природа, и когда вероятность наступления тех или иных событий многовариантна или неизвестна. Природные условия нередко сказываются и на эффективности работы промышленных предприятий.
5.2.5. Теория управления запасами
Возникновение теории управления запасами можно связать с работами Ф. Эджуфта и Ф. Харриса в конце XIX века, в которых исследовалась простая оптимизационная модель определения экономического размера партии поставки для складской системы с постоянным равномерным расходом и периодическим поступлением хранимого продукта.
Запасами называется любой ресурс на складе, который используется для удовлетворения будущих нужд. Примерами запасов могут служить полуфабрикаты, готовые изделия, материалы, различные товары, а также такие специфические товары, как денежная наличность, находящаяся в хранилище. Большинство организаций имеют примерно один тип системы планирования и контроля запасов. В банке используются методы контроля за количеством наличности, в больнице применяются методы контроля поставки различных медицинских препаратов.
Существует проблема классификации имеющихся в наличии запасов. Для решения этой задачи используется методика административного наблюдения. Цель ее заключается в определении той части запасов предприятия, которая требует наибольшего внимания со стороны отдела снабжения. Для этого каждый компонент запасов рассматривается по двум параметрам: а) его доля в общем количестве запасов предприятия; б) его доля в общей стоимости запасов предприятия.
Методика 20/80: в соответствии с этой методикой компоненты запаса, составляющие 20% его общего количества и 80% его общей стоимости, должны отслеживаться отделом снабжения более внимательно.
Методика XYZ-анализ делит запасы в соответствии с потреблением на три группы (постоянные, сезонные, не регулярные), такое деление способствует повышению эффективности принятия решений в области закупки и складирования.
Метод АВС предназначен для определения стоимости и других характеристик изделий, работ, услуг в целом и в разрезе их потребителей на основе систематизации расходов по функциям и ресурсам, задействованным в производстве и сбыте продукции, снабжении, маркетинге, техническом обеспечении, обслуживании покупателей.
ABC — один из методов, позволяющих указать на возможные пути улучшения стоимостных параметров деятельности предприятий, достичь улучшений в их работе по показателям стоимости, трудоемкости и производительности. Кроме того, расчеты, основанные на АВС-модели, обеспечивают получение большего объема информации для принятия управленческих решений в других проблемных областях, например при выборе клиентов или в ценообразовании.
Хорошо спроектированная ABC-система позволяет избежать искажений при распределении издержек благодаря минимизации усреднения накладных издержек, столь характерного для традиционных систем бухгалтерского учета. АВС - метод устраняет эти искажения, давая возможность определять реальную стоимость процессов, услуг, продукции. Одновременно он позволяет учитывать и некоторые другие специфические затраты, например на освоение производства, повышение качества продукции, послепродажное обслуживание покупателей и др.
Кроме моделей АВС, ХУZ, 20/80 и т.п. существуют и другие варианты управления запасами, прежде чем мы рассмотрим не которые из них, дадим определения основным понятиям в теории управления запасами.
Издержки выполнения заказа (издержки заказа) — накладные расходы, связанные с реализацией заказа. В промышленности такими издержками являются затраты на подготовительно-заготовочные операции.
Издержки хранения — расходы, связанные с физическим содержанием товаров на складе, плюс возможные проценты на капитал, вложенный в запасы. Обычно они выражаются или в абсолютных единицах, или в процентах от закупочной цены и связываются с определенным промежутком времени.
Упущенная прибыль — издержки, связанные с неудовлетворенным спросом, возникающим в результате отсутствия продукта на складе.
Совокупные издержки за период представляют собой сумму издержек заказа, издержек хранения и упущенного дохода. Иногда к ним прибавляются издержки на покупку товаров.
Срок выполнения заказа — срок между заказом и его выполнением.
Остановимся на краткой характеристике моделей управления запасами
Модель оптимального размера заказа.
Предпосылки: 1) темп спроса на товар известен и постоянен 2) получение заказа мгновенно; 3) отсутствуют количественные скидки при закупке больших партий товара; 4) единственно меняющиеся параметры — издержки заказа и хранения; 5) исключается дефицит в случае своевременного заказа.
Заказ, пополняющий запасы, поступает как одна партия. Уровень запасов убывает с постоянной интенсивностью пока не достигает нуля. В этой точке поступает заказ, размер которого равен ЕОQ, и уровень запасов восстанавливается до максимального значения. При этом оптимальным решением задачи будет тот размер заказа, при котором минимизируются общие издержки за период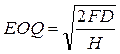 
EOQ - объем партии в единицах
F - стоимость выполнения одной партии заказа
D - общая потребность в запасах на период, ед.
H - затраты по хранению одной единицы запаса
Модель оптимального размера заказа в предположении, что получение заказа не мгновенно. Следовательно, нужно найти объем запасов, при котором необходимо делать новый заказ (RP). Введем предположение о том, что заказ может быть получен не мгновенно, а с течением времени. Тогда нам необходимо заранее делать заказ, чтобы в нужное время иметь достаточное количество товара на складе. Следовательно, нам необходимо найти тот уровень запасов, при котором делается новый заказ. Этот уровень называется точкой восстановления RP. Пусть MD — время выполнения заказа. Тогда RP величина спроса в единицу времени, умноженная на время выполнения заказа MD.
RP=MU*MD
RP - уровень запасов, при котором делается заказ, ед.
MU - максимальная дневная потребность в запасах, ед
MD - максимальное число дней выполнения заказа
Модель оптимального размера заказа в предположении, что допускается дефицит продукта и связанная с ним упущенная прибыль. Необходимо найти минимально допустимый уровень запасов. SS=RP-ЕОQ
. SS - минимальный уровень запасов
Модель производства и распределения. Необходимо рассматривать уровень ежедневного производства и уровень ежедневного спроса, для того чтобы определить максимально допустимый уровень запасов. MS=RP+EOQ
MS - максимальный уровень запасов, единиц
В предыдущей модели мы допускали, что пополнение запаса происходит единовременно, но в некоторых случаях, особенно в промышленном производстве, для комплектования партии товаров требуется значительное время и производство товаров для пополнения запасов происходит одновременно с удовлетворением спроса.
Модель с количественными скидками. Для увеличения объема продаж компании часто предлагают количественные скидки своим покупателям. Количественная скидка — сокращенная цена на товар в случае покупки большого количества этого товара.
Дата: 2019-02-02, просмотров: 187.
