Для проведения комплексной оценки хозяйственной деятельности предприятия сравнения по одному критерию явно недостаточно. В развернутом анализе экономические субъекты сравниваются сразу по нескольким критериям (например, по уровню рентабельности, оборачиваемости, росту продаж и т.д.). Многомерные сравнения необходимы для комплексной оценки результатов хозяйствования.
Комплексная оценка предполагает изучение совокупности показателей, которые дают многостороннюю характеристику изучаемого явления или объекта. Комплексная оценка применяется для анализа большинства экономических процессов, для исследования обобщающих данных о результатах деятельности предприятия.
При проведении в ходе комплексной оценки многомерных сравнений используются такие приемы, как построение многоосевых диаграмм показателей, методы ранжирования и расчета интегральных показателей, кластерный анализ (таксонометрический).
Последовательность оценки с использованием многоосевых диаграмм показателей следующая:
- выбираются критерии оценки;
- изображается окружность и наносятся оси для каждого критерия;
- выбирается область предпочтительных значений по построенным осям;
- фактические значения откладываются на осях и соединяются замкнутой линией.
В экономических исследованиях достаточно часто, приходится сталкиваться с проблемой группировки предприятий по нескольким признакам, для решения данной проблемы способы классических построений группировочных таблиц не приемлемы.
Кластерный анализ – один из методов многомерного анализа, предназначенный для группировки совокупности, элементы которой характеризуются многими признаками. Значения каждого из признаков служат координатами каждой единицы изучаемой совокупности в многомерном пространстве признаков. Каждое наблюдение, характеризующиеся значениями нескольких показателей, можно представить как точку в пространстве этих показателей, значения которых рассматриваются как координаты в многомерном пространстве.
Рассмотрим алгоритм кластерного анализа:
- от исходной совокупности наблюдений осуществляется переход к матрице нормированных значений;
- рассматривается симметричная матрица расстояний между элементами нормированной матрицы. Расстояние в n – мерном пространстве рассчитывается как модуль вектора евклидова (хеммингова) пространства, но каждая координата умножается на свой вес;
- поскольку матрица расстояний представляет собой симметричную матрицу, то для дальнейшего анализа выбирается ее верхняя (нижняя) половина. Элементы на главной диагонали исключаются из рассмотрения. Среди всех элементов рассматриваемой матрицы находится минимальный элемент. Строка найденного минимального элемента соответствует одному номеру наблюдений, а столбец другому. Эти два наблюдения объединяются в один кластер. Кластер в дальнейшем рассматривается как первый элемент исходной совокупности. При этом второй элемент исключается из дальнейшего рассмотрения. Количество элементов, вошедших в тот или иной кластер фиксируется. Таким образом размерность исходной информации уменьшается на единицу;
- вся процедура повторяется до тех пор, пока количество кластеров не станет равным заданному.
Пример 1
По данным, представленным в таблице 4.27., проведем классификацию n=5 цехов предприятий по двум показателям: расходы (млн.руб.) – x(1): и уровень прибыли x(2)
Таблица 4.27.
Показатели по цехам предприятия
| № цеха | 1 | 2 | 3 | 4 | 5 |
| Xi(1) | 2 | 4 | 8 | 12 | 13 |
| Xi(2) | 10 | 7 | 6 | 11 | 9 |
Классификацию проведем по иерархическому агломеративному алгоритму с использованием обычного и взвешенного (w 1 =0,05; w 2 =0,95) евклидова расстояния, а также принципов: “ближайшего” и “дальнего” соседа, центра тяжести и средней связи.
1. Проведем классификацию, выбрав при обычном евклидовом расстоянии принцип “ближайшего соседа”.
Построим матрицу расстояний
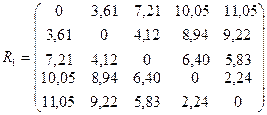
Матрица расстояний рассчитана на основе обычного евклидова расстояния между наблюдениями.
Из матрицы расстояний следует, что объекты 4 и 5 наиболее близки r4,5=2,24 и поэтому объединим их в один кластер. После объединения объектов имеем четыре кластера: S1, S2, S3, S(4,5).
очевидно, что r1,1=0.
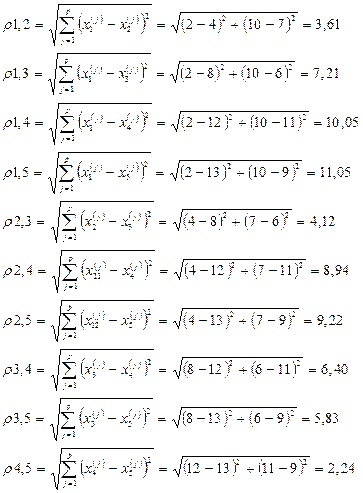
Примечание: На основании предварительного качественного анализа было выдвинуто предположение, что по поведению три первые цеха принадлежат одной типологической группе, а два последних (4 и 5) – другой, что согласуется с расположением пяти наблюдений на плоскости, представленных на рис. .
12
10
8
6
4
2
0
| 5 | 10 | 15 |
Рис. Исходные данные для классификации
Расстояние между кластерами будем находить по принципу “ближайшего соседа”, воспользовавшись формулой пересчета. Так расстояние между кластером S1 и кластером S(4,5) равно:
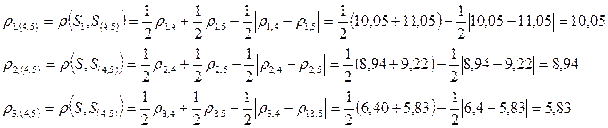
Мы видим, что расстояние r1,(4,5) равно расстоянию от объекта 1 до ближайшего к нему объекта, входящего в кластер S(4,5), т.е. r1,(4,5)= r1,4=10,05. Проводя анологичные расчеты, получим матрицу расстояний
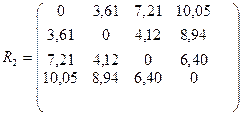
Объединим наблюдения 1 и 2, имеющие наименьшее расстояние r1,2=3,61. После объединения имеем три кластера S(1,2), S3, и S(4,5)
Вновь строим матрицу расстояний. Для этого необходимо рассчитать расстояния до кластера S(1,2).
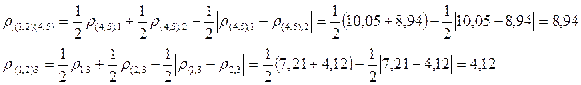
Получим новую матрицу расстояний
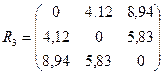
Объединим кластеры S(1,2) и S3, расстояние между которыми, согласно матрице R3, минимально 4,12. В результате этого получим два кластера: S(1,2,3) и S(4,5).
p
6 5,83
5 4,12
4 3,61
3 2,24
2
1
0
| 1 | 2 | 3 | 4 | 5 | цеха |
Рис. Дендрограмма (обычное евклидово расстояние, ближайший сосед)
Определим между ними расстояние:
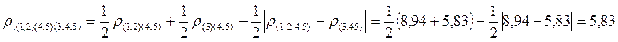
На основании графического представления результатов и кластерного анализа можно сделать вывод, что наилучшим является разбиение пяти цехов на два кластера: S(1,2,3) и S(4,5) , когда пороговое расстояние находится в интервале 4,12 < pпор < 5,83.
2. Проведем классификацию, выбрав при обычном евклидовом расстоянии принцип «дальнего соседа».
Как и в предыдущем расчете, мы используем обычное евклидово расстояние, поэтому матрица R 1 останется без изменения. Согласно алгоритму объединим цеха 4 и 5 в один кластер, как наиболее близкие по расстоянию 2,24. После объединения имеем четыре кластера S(1), S(2), S(3) и S(4,5).
В виду того, что расстояние между кластерами измеряем по принципу «дальнего соседа», то воспользуемся формулой пересчета:
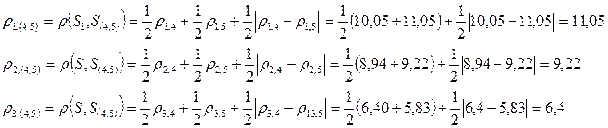
Таким образом, расстояние между кластерами 1 и (4,5) максимально и составляет 11,05. Построим новую матрицу расстояний:
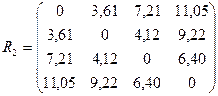
Объединим объекты 1 и 2 в один кластер, как наиболее близкие (расстояние между ними 3,61. После объединения имеем три кластера: S(1,2), S(3) и S(4,5). Определим новые расстояния между кластерами:
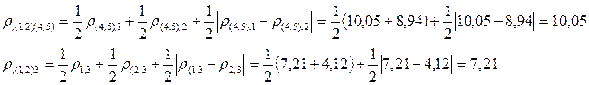Строим матрицу расстояний R 3, используя принцип «дальнего соседа».
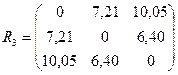
Объединим кластеры S(3) и S(4,5), так как расстояние между ними минимально 6,40. Определим расстояние между новыми кластерами S(1,2) и S(3,4,5):
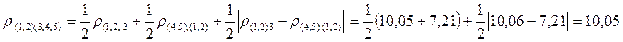
Составим матрицу расстояний:
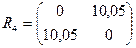
На основании графического представления результатов кластерного анализа по принципу «дальнего соседа» можно сделать вывод, что наилучшим является разбиение пяти цехов на два кластера: S(1,2) и S(3,4,5) , когда пороговое расстояние находится в интервале 6,40 < pпор < 10,05.
Таким образом, используя принцип «дальнего соседа» мы получили разбиение цехов, которое отличается от разбиения по принципу «ближнего соседа».
p
12
10 10,05
8
6 6,40
4 3,61
2 2,24
0
| 1 | 2 | 3 | 4 | 5 | цеха |
Рис. Дендрограмма (обычное евклидово расстояние, «дальний сосед»)
3. Классификация на основе обычного евклидова расстояния
и принципа «центра тяжести».
Так как мы используем обычное евклидово расстояние, то матрица R 1 останется без изменения. Согласно алгоритма объединим в один кластер цеха 4 и 5, как наиболее близкие 2,24.
Кластер S(4,5) охарактенизуем его центром тяжести, для этого используем вектор средних :
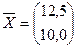
Расстояние от этого кластера до объектов равно:
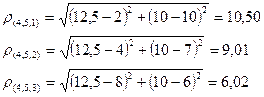
Тогда матрица расстояний примет вид:
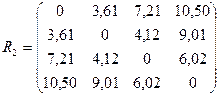
Объединим объекты 1 и 2, расстояние между которыми минимальное 3,61. Тогда кластер будет характеризоваться центром тяжести:
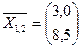
Определим новые расстояния:
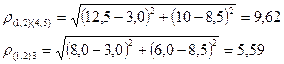
Тогда матрица расстояний примет вид:
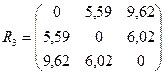
Объединим кластеры S(1,2) и S(3), так как расстояние между ними минимально 5,59. Определим его вектор средних
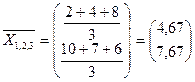
Найдем расстояние между кластерами S(1,2,3) и S(4,5)
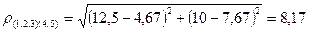
Составим матрицу расстояний:
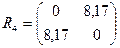
На основании графического представления результатов кластерного анализа по принципу «центра тяжести» можно сделать вывод, что наилучшим является разбиение пяти цехов на два кластера: S(1,2,3) и S(,4,5) , когда пороговое расстояние находится в интервале 5,59 < pпор < 8,17.
Таким образом, используя принцип «центр тяжести» мы получили разбиение цехов, которое отличается от разбиения по принципу «дальнего соседа», но совпадает с расчетами в первом варианте по принципу «ближнего соседа».
Графические результаты классификации представлены на рис.
p 8,17
8
7
6 5,59
5
4 3,61
3
2 2,24
1
0
| 1 | 2 | 3 | 4 | 5 | цеха |
Рис. Дендрограмма (обычное евклидово расстояние, «центр тяжести»)
4. Классификация на основе обычного евклидова расстояния
и принципа «средней связи».
Так как мы используем обычное евклидово расстояние, то матрица R 1 останется без изменения. Согласно алгоритма объединим в один кластер цеха 4 и 5, как наиболее близкие 2,24. Расстояние от этого кластера до объектов по принципу «средней связи» равно:
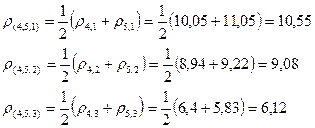
Тогда матрица расстояний примет вид:
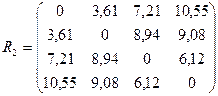
Объединим объекты 1 и 2, расстояние между которыми минимальное 3,61. Определим новые расстояния:
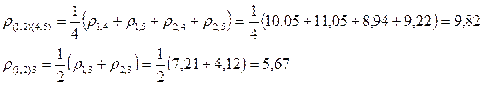
Тогда матрица расстояний примет вид:
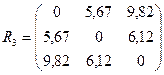
Объединим кластеры S(1,2) и S(3), так как расстояние между ними минимально 5,67. Найдем расстояние между кластерами S(1,2,3) и S(4,5)
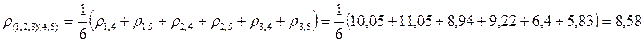Графические результаты классификации представлены на рис.
p 8,58
8
7
6 5,67
5
4 3,61
3
2 2,24
1
0
| 1 | 2 | 3 | 4 | 5 | цеха |
Рис. Дендрограмма (обычное евклидово расстояние, «средняя связь»)
На основании графического представления результатов кластерного анализа по принципу «средней связи» можно сделать вывод, что наилучшим является разбиение пяти цехов на два кластера: S(1,2,3) и S(,4,5) , когда пороговое расстояние находится в интервале 5,67 < pпор < 8,58.
Таким образом, используя принцип «средней связи» мы получили разбиение цехов, которое отличается от разбиения по принципу «дальнего соседа», но совпадает с расчетами в первом варианте по принципу «ближнего соседа» и «центра тяжести».
Следовательно при классификации 5 цехов предприятия предпочтительным является объединение в одну группу 4 и 5 цеха, а во вторую 1,2 и 3 цехов, что подтверждено тремя вариантами расчетов из четырех.
Дата: 2019-02-02, просмотров: 240.
