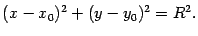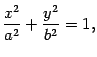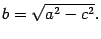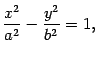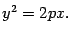Приведение к каноническому виду общего уравнения кривой второго порядка
Рассмотрим в декартовой прямоугольной системе координат Oxy уравнение второго порядка общего вида:
Аx2 + 2Вxy + Сy2 + 2Dx + 2Еy + F = 0,
где не все коэффициенты А, В и С равны одновременно нулю.
Оно задаёт кривую второго порядка.
Наша цель: поменять систему координат так, чтобы максимально упростить данное уравнение.
Для этого сначала (если B  0) повернём исходный базис (координатные оси Ox и Oy) на угол α против часовой стрелки таким образом, чтобы новые оси Ox’ и Oy’ стали параллельны осям кривой, при этом исчезнет слагаемое 2Вxy:
0) повернём исходный базис (координатные оси Ox и Oy) на угол α против часовой стрелки таким образом, чтобы новые оси Ox’ и Oy’ стали параллельны осям кривой, при этом исчезнет слагаемое 2Вxy:
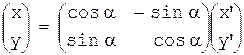 ,
,
где  -
-
матрица линейного преобразования: поворот на угол α против часовой стрелки.
Или, наоборот, 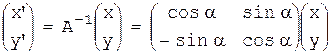 .
.
A(x’cosα - y’sinα)2 + 2B(x’cosα - y’sinα)(x’sinα + y’cosα)+
+ C(x’sinα + y’cosα)2 +
+ 2D(x’cosα - y’sinα) + 2E(x’sinα + y’cosα) + F = 0
Выберем угол α так, чтобы коэффициент при произведении x’y’ обратился в ноль, т.е. чтобы выполнялось равенство
-2Acosαsinα + 2B(cos2α - sin2α) + 2Csinαcosα = 0
или 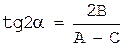
или 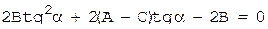
В новой системе координат Ox’y’ (после поворота на угол α), учитывая, что
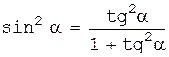 ;
; 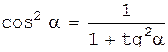 ,
,
уравнение будет иметь вид
А’x’2 + С’y’2 + 2D’x’ + 2Е’y’ + F’ = 0,
где коэффициенты А’ и С’ не равны одновременно нулю.
Следующий этап упрощения заключается в параллельном переносе осей Ox’ и Oy’ до совпадения их с осями кривой, при этом начало координат совпадёт с центром (или вершиной, в случае параболы) кривой. Техника преобразований на данном этапе заключается в выделении полного квадрата.
Таким образом, мы получим канонические уравнения кривых второго порядка.
Всего возможны 9 качественно различных случаев (включая случаи вырождения и распадения):
1. 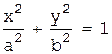 (эллипс),
(эллипс),
2. 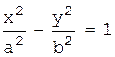 (гипербола),
(гипербола),
3.  px (парабола),
px (парабола),
4. 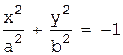 (мнимый эллипс),
(мнимый эллипс),
5. 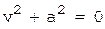 (пара мнимых параллельных прямых),
(пара мнимых параллельных прямых),
6. 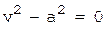 (пара параллельных прямых),
(пара параллельных прямых),
7. 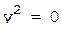 (пара совпавших прямых),
(пара совпавших прямых),
8. 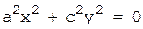 (точка (пара мнимых пересекающихся прямых)),
(точка (пара мнимых пересекающихся прямых)),
9. 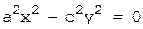 (пара пересекающихся прямых).
(пара пересекающихся прямых).
Рассмотрим пример.
Записать классическое уравнение гиперболы  в канонической форме. Сделать чертёж.
в канонической форме. Сделать чертёж.
Решение.
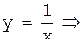 yx-1=0,
yx-1=0,
сделаем замену переменных:
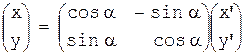 , тогда
, тогда
(x’cosα - y’sinα)(x’sinα + y’cosα)-1 = 0,
x’2cos2α - y’2cosαsinα + x’y’(cos2α - sin2α) – 1 = 0,
(cos2α - sin2α) = 0 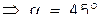
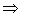
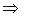
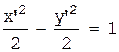 .
.
Совершенно аналогично, каноническое уравнение для гиперболы
 будет иметь вид:
будет иметь вид:  или
или 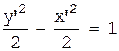 .
.
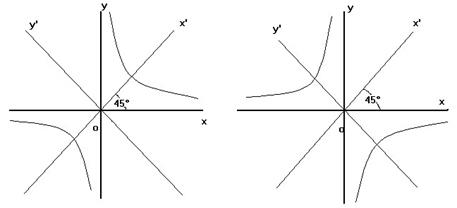
Кривые 2-го порядка со смещенными центрами (вершинами)
Если в общем уравнении кривой 2-го порядка
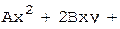
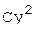
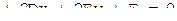 ,
,
в частности В = 0, то есть отсутствует член с произведением переменных, то это означает, что оси кривой параллельны координатным. Рассмотрим уравнение:

(  A и C
A и C 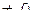 одновременно). Можно показать, что при этом:
одновременно). Можно показать, что при этом:
1) Если АС > 0 (коэффициенты при квадратах переменных одного знака), то уравнение определяет эллипс;
2) Если АС < 0 (коэффициенты при квадратах переменных имеют разные знаки), то уравнение определяет гиперболу;
3) Если АС = 0 (один из членов с квадратом переменных отсутствует), то этим уравнением определяется парабола.
В каждом из случаев 1), 2), 3) могут встретиться вырожденные кривые, которыми мы заниматься не будем.
Для того, чтобы понять, как именно расположена кривая относительно системы координат и каковы ее параметры, уравнение можно преобразовать способом выделения полных квадратов. После этого уравнение примет вид одного из невырожденных уравнений кривой 2-го порядка со смещенным центром:
1) 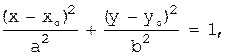
это уравнение эллипса с центром 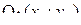 и осями, параллельными осям
и осями, параллельными осям 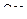 и
и 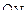 ;
;
2) 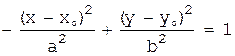 и
и  ,
,
эти уравнения определяют гиперболы с центром 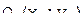 и осями, параллельными координатным;
и осями, параллельными координатным;
3) 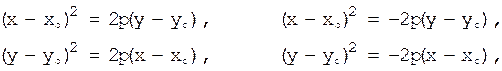
это параболы с вершиной 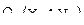 и осью, параллельной одной из координатных.
и осью, параллельной одной из координатных.
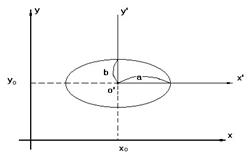
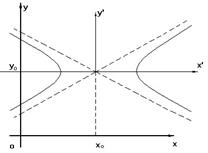
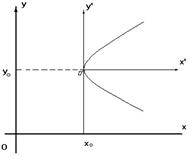
Пусть на плоскости задана прямоугольная декартова система координат.
Определение 12.1 Кривой второго порядка называется множество точек, координаты которых удовлетворяют уравнению второго порядка
|
| (8.1) |
где  -- вещественные числа, и хотя бы одно из чисел
-- вещественные числа, и хотя бы одно из чисел 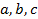 отлично от нуля
отлично от нуля
Окружность
Начнем с определения окружности, известного из школьного курса математики.
Определение 12.2 Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности.
Получим уравнение окружности, если известны ее центр и радиус.
Теорема 12.1 Окружность радиуса  с центром в точке
с центром в точке 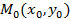 имеет уравнение
имеет уравнение
|
| (8.2) |
Доказательство. Пусть 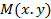 -- текущая точка окружности. По определению окружности расстояние
-- текущая точка окружности. По определению окружности расстояние 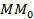 равно
равно  (рис. 8.1)
(рис. 8.1)

Рис.8.1.Окружность
По формуле для плоскости получаем, что точки окружности и только они удовлетворяют уравнению
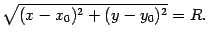
Обе части уравнения неотрицательны. Поэтому после возведения их в квадрат получим эквивалентное уравнение (8.2).
Если в уравнении (8.2) раскрыть скобки и привести подобные члены, то вид его изменится. Однако любое уравнение окружности с помощью тождественных преобразований можно привести к виду (8.2). Для этого достаточно выделить полные квадраты по переменным 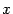 и
и 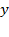 .
.
Эллипс
Определение 8.3 Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная.
Для эллипса можно дать еще несколько эквивалентных определений. Желающие могут познакомиться с ними в более серьезных учебниках по аналитической геометрии. Здесь же отметим только то, что эллипс -- это кривая, получающаяся как проекция на плоскость 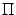 окружности, лежащей в плоскости, которая образует острый угол с плоскостью
окружности, лежащей в плоскости, которая образует острый угол с плоскостью 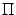 .
.
В отличие от окружности, записать в "удобном" виде уравнение эллипса в произвольной системе координат не удается. Поэтому для фиксированного эллипса приходится подбирать систему координат так, чтобы его уравнение было достаточно простым.
Пусть 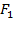 и
и 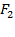 -- фокусы эллипса. Начало
-- фокусы эллипса. Начало  системы координат расположим на середине отрезка
системы координат расположим на середине отрезка 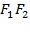 . Ось
. Ось 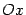 направим вдоль этого отрезка, ось Oy-- перпендикулярно к этому отрезку (рис. 12.3).
направим вдоль этого отрезка, ось Oy-- перпендикулярно к этому отрезку (рис. 12.3).
Теорема 12.2 Пусть сумма расстояний от точки эллипса до фокусов равна  , а расстояние между фокусами --
, а расстояние между фокусами -- 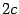 . Тогда в выбранной системе координат эллипс имеет уравнение
. Тогда в выбранной системе координат эллипс имеет уравнение
|
| (12.4) |
где
|
| (12.5) |
Доказательство. Пусть 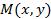 -- текущая точка эллипса. По определению эллипса
-- текущая точка эллипса. По определению эллипса 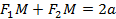 . Из треугольника
. Из треугольника  (рис. 12.3) видно, что
(рис. 12.3) видно, что 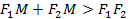 , то есть
, то есть 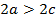 ,
, 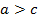 , и поэтому число
, и поэтому число  существует.
существует.
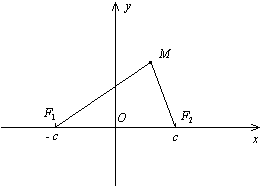
Рис.12.3.
Фокусами в выбранной системе координат являются точки 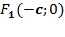 ,
,  .
.
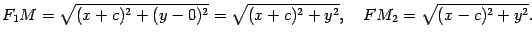
Тогда по определению эллипса
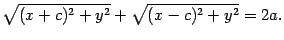
Пренесем один из корней вправо и обе части возведем в квадрат:
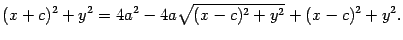
После того, как раскроем скобки и приведем подобные члены, приходим к выражению
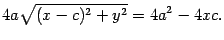
Разделим обе части этого уравнения на 4 и возведем в квадрат
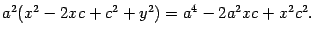
Раскроем скобку и приведем подобные члены

Учитывая, что 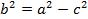 , имеем равенство
, имеем равенство
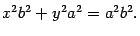
Наконец, разделив обе части на  , получим уравнение (12.4).
, получим уравнение (12.4).
Уравнение (12.4) называется каноническим уравнением эллипса.
Прежде, чем нарисовать эллипс, выясним некоторые его свойства.
Предложение 12.1 Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центром симметрии. Если эллипс задан каноническим уравнением ( 12.4 ), то его осями симметрии служат оси 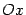 и
и 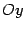 , начало координат -- центр симметрии.
, начало координат -- центр симметрии.
Доказательство. Можно было бы провести доказательство на основе определения эллипса (предлагаем читателю попробовать сделать это), но для усиления аналитического аспекта мы проведем доказательство на основе уравнения (12.4).
Пусть эллипс задан уравнением (12.4) и 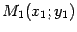 -- какая-то точка эллипса. Тогда
-- какая-то точка эллипса. Тогда
|
| (12.6) |
Точка 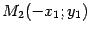 является точкой, симметричной точке
является точкой, симметричной точке 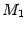 относительно оси
относительно оси 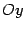 (рис. 12.4).
(рис. 12.4).
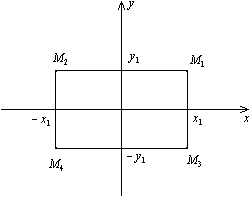
Рис.12.4.Симметрия точек
Вычисляем значение левой части уравнения (12.4) в точке 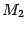
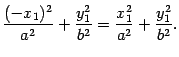
В силу равенства (12.6) получаем
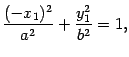
следовательно, точка  лежит на эллипсе. Точка
лежит на эллипсе. Точка  является точкой симметричной
является точкой симметричной  точке относительно оси
точке относительно оси 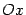 (рис. 12.4). Для нее аналогичным путем убеждаемся, что
(рис. 12.4). Для нее аналогичным путем убеждаемся, что

то есть  является точкой эллипса. Наконец точка
является точкой эллипса. Наконец точка 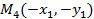 является симметричной точке
является симметричной точке 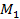 относительно начала координат (рис. 12.4). Повторяя предыдущие рассуждения, получим, что и эта точка тоже лежит на эллипсе. Итак, утверждение предложения доказано, если эллипс имеет уравнение (12.4). А так как по теореме 12.2 любой эллипс в некоторой системе координат имеет такое уравнение, то предложение полностью доказано.
относительно начала координат (рис. 12.4). Повторяя предыдущие рассуждения, получим, что и эта точка тоже лежит на эллипсе. Итак, утверждение предложения доказано, если эллипс имеет уравнение (12.4). А так как по теореме 12.2 любой эллипс в некоторой системе координат имеет такое уравнение, то предложение полностью доказано.
Гипербола
Из школьного курса математики известно, что кривая, задаваемая уравнением 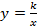 , где
, где  -- число, называется гиперболой. Однако это -- частный случай гиперболы (равносторонняя гипербола).
-- число, называется гиперболой. Однако это -- частный случай гиперболы (равносторонняя гипербола).
Определение 12.5 Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.
Так же, как и в случае эллипса, для получения уравнения гиперболы выберем подходящую систему координат. Начало координат расположим на середине отрезка между фокусами, ось 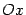 направим вдоль этого отрезка, а ось ординат -- перпендикулярно к нему.
направим вдоль этого отрезка, а ось ординат -- перпендикулярно к нему.
Теорема 12.3 Пусть расстояние между фокусами  и
и 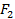 гиперболы равно
гиперболы равно 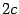 , а абсолютная величина разности расстояний от точки гиперболы до фокусов равна
, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна  . Тогда гипербола в выбранной выше системе координат имеет уравнение
. Тогда гипербола в выбранной выше системе координат имеет уравнение
|
| (12.8) |
где
|
| (12.9) |
Доказательство. Пусть 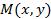 -- текущая точка гиперболы (рис. 12.9).
-- текущая точка гиперболы (рис. 12.9).
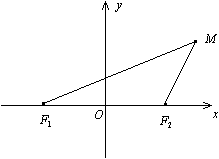
Рис.12.9.
Так как разность двух сторон треугольника меньше третьей стороны, то 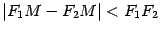 , то есть
, то есть 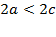 ,
, 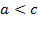 . В силу последнего неравенства вещественное число
. В силу последнего неравенства вещественное число 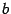 , определяемое формулой (12.9), существует.
, определяемое формулой (12.9), существует.
По условию, фокусы -- 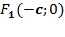 ,
,  . По формуле (10.4) для случая плоскости получаем
. По формуле (10.4) для случая плоскости получаем
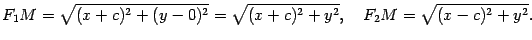
По определению гиперболы
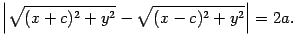
Это уравнение запишем в виде
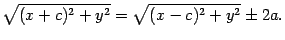
Обе части возведем в квадрат:
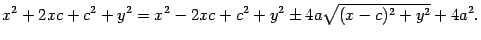
После приведения подобных членов и деления на 4, приходим к равенству
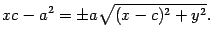
Опять обе части возведем в квадрат:
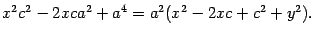
Раскрывая скобку и приводя подобные члены, получим
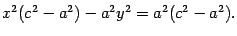
С учетом формулы (12.9) уравнение принимает вид
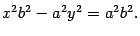
Разделим обе части уравнения на  и получим уравнение (12.8)
и получим уравнение (12.8)
Уравнение (12.8) называется каноническим уравнением гиперболы.
Предложение 12.3 Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением, то ее осями симметрии служат координатные оси 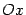 и Oy, а начало координат -- центр симметрии гиперболы.
и Oy, а начало координат -- центр симметрии гиперболы.
Доказательство. Проводится аналогично доказательству предложения 12.1.
Проведем построение гиперболы, заданной уравнением (12.8). Заметим, что из-за симметрии достаточно построить кривую только в первом координатном угле. Выразим из канонического уравнения y как функцию 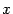 , при условии, что
, при условии, что 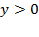 ,
,

и построим график этой функции.
Область определения -- интервал 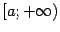 ,
, 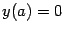 , функция монотонно растет. Производная
, функция монотонно растет. Производная
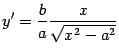
существует во всей области определения, кроме точки 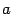 . Следовательно, график -- гладкая кривая (без углов). Вторая производная
. Следовательно, график -- гладкая кривая (без углов). Вторая производная
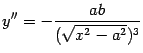
во всех точках интервала 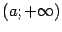 отрицательна, следовательно, график -- выпуклый вверх.
отрицательна, следовательно, график -- выпуклый вверх.
Проверим график на наличие асимптоты при 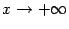 . Пусть асимптота имеет уравнение
. Пусть асимптота имеет уравнение 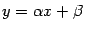 . Тогда по правилам математического анализа
. Тогда по правилам математического анализа
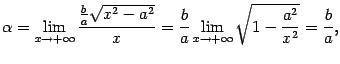
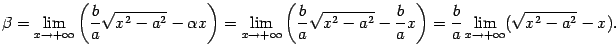
Выражение под знаком предела домножим и разделим на 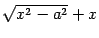 . Получим
. Получим
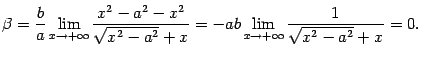
Итак, график функции имеет асимптоту 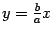 . Из симметрии гиперболы следует, что
. Из симметрии гиперболы следует, что 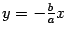 -- тоже асимптота. Остается неясным характер кривой в окрестности точки
-- тоже асимптота. Остается неясным характер кривой в окрестности точки 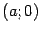 , а именно, образует ли график
, а именно, образует ли график 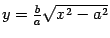 и симметричная ему относительно оси
и симметричная ему относительно оси  часть гиперболы в этой точке угол или гипербола в этой точке -- гладкая кривая (есть касательная). Для решения этого вопроса выразим из уравнения (12.8)
часть гиперболы в этой точке угол или гипербола в этой точке -- гладкая кривая (есть касательная). Для решения этого вопроса выразим из уравнения (12.8) 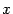 через
через  :
:

Очевидно, что данная функция имеет производную в точке 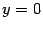 ,
, 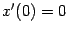 , и в точке
, и в точке 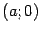 у гиперболы есть вертикальная касательная. По полученным данным рисуем график функции
у гиперболы есть вертикальная касательная. По полученным данным рисуем график функции 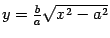 (рис. 12.10).
(рис. 12.10).
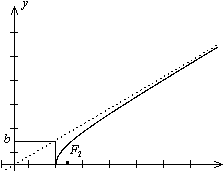
Рис.12.10.График функции 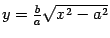
Окончательно, используя симметрию гиперболы, получаем кривую рисунка 12.11.
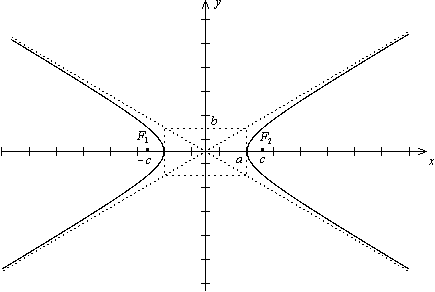
Рис.12.11.Гипербола
Определение 12.6 Точки пересечения гиперболы, заданной каноническим уравнением (12.8), с осью  называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками
называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками 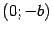 и
и 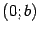 называется мнимой осью. Числа
называется мнимой осью. Числа 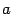 и
и 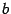 называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром. Величина
называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром. Величина 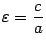 называется эксцентриситетом гиперболы.
называется эксцентриситетом гиперболы.
Замечание 12.3 Из равенства (12.9) следует, что 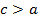 , то есть у гиперболы
, то есть у гиперболы 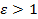 . Эксцентриситет
. Эксцентриситет 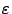 характеризует угол между асимптотами, чем ближе
характеризует угол между асимптотами, чем ближе 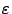 к 1, тем меньше этот угол.
к 1, тем меньше этот угол.
Замечание 12.4 В отличие от эллипса в каноническом уравнении гиперболы соотношение между величинами 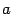 и
и 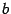 может быть произвольным. В частности, при
может быть произвольным. В частности, при 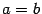 мы получим равностороннюю гиперболу, известную из школьного курса математики. Ее уравнение имеет знакомый вид
мы получим равностороннюю гиперболу, известную из школьного курса математики. Ее уравнение имеет знакомый вид 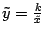 , если взять
, если взять 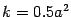 , а оси
, а оси  и
и  направить по биссектрисам четвертого и первого координатных углов (рис. 12.12).
направить по биссектрисам четвертого и первого координатных углов (рис. 12.12).

Рис.12.12.Равносторонняя гипербола 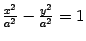
Для отражения на рисунке качественных характеристик гиперболы достаточно определить ее вершины, нарисовать асимптоты и нарисовать гладкую кривую, проходящую через вершины, приближающуюся к асимптотам и похожую на кривую рисунка 12.10.
Парабола
В школьном курсе математики достаточно подробно изучалась парабола, которая, по определению, являлась графиком квадратного трехчлена. Здесь мы дадим другое (геометрическое) определение параболы.
Определение 12.7 Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.
Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса  опустим перпендикуляр
опустим перпендикуляр  на директрису
на директрису  . Начало координат
. Начало координат 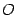 расположим на середине отрезка
расположим на середине отрезка 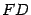 , ось
, ось 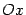 направим вдоль отрезка
направим вдоль отрезка 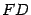 так, чтобы ее направление совпадало с направлением вектора
так, чтобы ее направление совпадало с направлением вектора 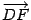 . Ось
. Ось 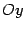 проведем перпендикулярно оси
проведем перпендикулярно оси 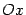 (рис. 12.15).
(рис. 12.15).
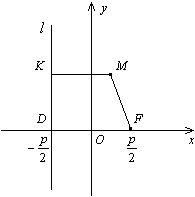
Рис.12.15.
Теорема 12.4 Пусть расстояние между фокусом 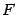 и директрисой
и директрисой 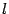 параболы равно
параболы равно 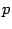 . Тогда в выбранной системе координат парабола имеет уравнение
. Тогда в выбранной системе координат парабола имеет уравнение
|
| (12.10) |
Доказательство. В выбранной системе координат фокусом параболы служит точка 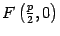 , а директриса имеет уравнение
, а директриса имеет уравнение  (рис. 12.15).
(рис. 12.15).
Пусть 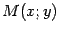 -- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим
-- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим
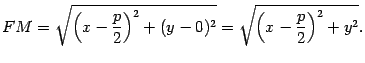
Расстоянием от точки  до директрисы
до директрисы  служит длина перпендикуляра
служит длина перпендикуляра  , опущенного на директрису из точки
, опущенного на директрису из точки  . Из рисунка 12.15 очевидно, что
. Из рисунка 12.15 очевидно, что 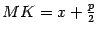 . Тогда по определению параболы
. Тогда по определению параболы 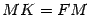 , то есть
, то есть
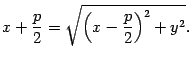
Возведем обе части последнего уравнения в квадрат:
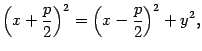
откуда
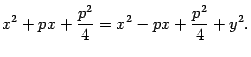
После приведения подобных членов получим уравнение (12.10).
Уравнение (12.10) называется каноническим уравнением параболы.
Предложение 12.4 Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью 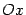 .
.
Доказательство. Проводится так же, как и доказательство (предложения 12.1).
Точка пересечения оси симметрии с параболой называется вершиной параболы.
Если переобозначить переменные 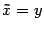 ,
, 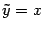 , то уравнение (12.10) можно записать в виде
, то уравнение (12.10) можно записать в виде
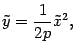
который совпадает с обычным уравнением параболы в школьном курсе математики. Поэтому параболу нарисуем без дополнительных исследований (рис. 12.16).
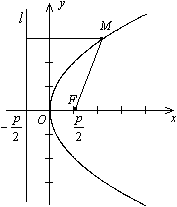
Рис.12.16.Парабола

Дата: 2019-02-02, просмотров: 506.