В дальнейшем полагаем, что в пространстве определена некая прямоугольная декартова система координат — каждая точка пространства однозначно определена своими координатами.
Уравнение вида 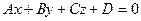 — линейное алгебраическое уравнение первой степени или просто — линейное уравнение.
— линейное алгебраическое уравнение первой степени или просто — линейное уравнение.
Уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору.
Пусть задана точка 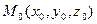 и вектор
и вектор 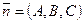 . Как отличить точки принадлежащие плоскости, проходящей через точку
. Как отличить точки принадлежащие плоскости, проходящей через точку 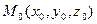 , перпендикулярно вектору
, перпендикулярно вектору 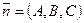 , от точек, которые этой плоскости не принадлежат?
, от точек, которые этой плоскости не принадлежат?
Можно предложить такой способ: точка 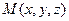 принадлежит плоскости тогда и только тогда, когда вектор
принадлежит плоскости тогда и только тогда, когда вектор 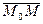 ортогонален вектору
ортогонален вектору 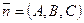 , т.е. тогда и только тогда, когда
, т.е. тогда и только тогда, когда  .
.
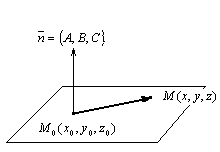
Тогда, поскольку 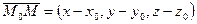 получим линейное уравнение
получим линейное уравнение
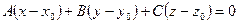 . Это уравнение плоскости, проходящей через точку
. Это уравнение плоскости, проходящей через точку 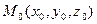 нормальным вектором
нормальным вектором 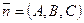 .
.
Замечание. Вектор, ортогональный плоскости, ортогонален любому вектору, принадлежащему плоскости. Такой вектор называю нормальным вектором плоскости.
Общее уравнение плоскости. Раскроем скобки в уравнении плоскости, проходящей через точку 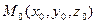 нормальным вектором
нормальным вектором 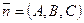 :
: 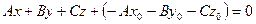 и обозначим
и обозначим 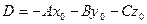 .
.
Получим общее уравнение плоскости 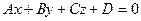 .
.
Из предыдущих рассуждений ясно, что коэффициенты 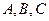 общего уравнения плоскости
общего уравнения плоскости  определяют нормальный вектор этой плоскости:
определяют нормальный вектор этой плоскости: 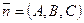 .
.
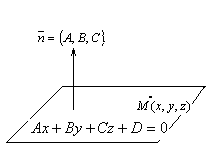
Неполные уравнения плоскости. Уравнение 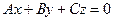 определяет плоскость, проходящую через начало координат. Действительно, подставив в уравнение плоскости координаты начала координат, О(0, 0, 0), получим тождество.
определяет плоскость, проходящую через начало координат. Действительно, подставив в уравнение плоскости координаты начала координат, О(0, 0, 0), получим тождество.
Уравнение  определяет плоскость, параллельную оси 0x.
определяет плоскость, параллельную оси 0x.
Действительно, нормальный вектор этой плоскости 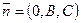 ортогонален орту оси 0x — вектору
ортогонален орту оси 0x — вектору 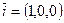 :
: 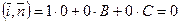 .
.
Уравнение 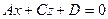 — уравнение плоскости, параллельной оси 0y, а
— уравнение плоскости, параллельной оси 0y, а
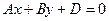 — уравнение плоскости, параллельной оси 0z.
— уравнение плоскости, параллельной оси 0z.
Уравнение 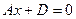 — уравнение плоскости, параллельной плоскости y0z, поскольку ее нормальный вектор
— уравнение плоскости, параллельной плоскости y0z, поскольку ее нормальный вектор 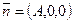 коллинеарен вектору
коллинеарен вектору 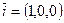 ;
;
Уравнение 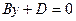 — уравнение плоскости, параллельной плоскости x0z, а уравнение
— уравнение плоскости, параллельной плоскости x0z, а уравнение  — уравнение плоскости, параллельной плоскости x0y.
— уравнение плоскости, параллельной плоскости x0y.
Нарисуйте!
Уравнение плоскости в отрезках. Рассмотрим плоскость, которая не проходит через начало координат. Ее уравнение 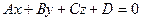 ,
, 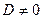 .
.
Преобразуем уравнение: 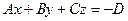 ,
, 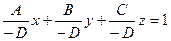 ,
, 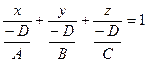 и обозначим
и обозначим 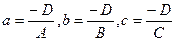 .
.
Получим уравнение 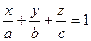 — уравнение плоскости «в отрезках».
— уравнение плоскости «в отрезках».
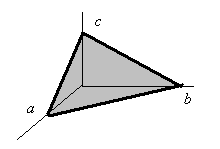
Плоскость, заданную таким уравнением легко рисовать. На рисунке изображен случай, когда 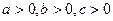 . Действительно, легко убедиться, что точки с координатами (a, 0,0), (0,b,0), (0,0,c) — это точки пересечения плоскости с координатными осями.
. Действительно, легко убедиться, что точки с координатами (a, 0,0), (0,b,0), (0,0,c) — это точки пересечения плоскости с координатными осями.
Уравнение плоскости, проходящей через три заданные точки. Известно, что три точки, не лежащие на одной прямой, однозначно определяют плоскость.
Как отличить точки принадлежащие плоскости, проходящей через точки 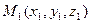 ,
, 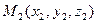 ,
, 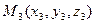 , от точек, которые этой плоскости не принадлежат? Понятно, что точка
, от точек, которые этой плоскости не принадлежат? Понятно, что точка 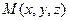 принадлежит плоскости тогда и только тогда, когда компланарны векторы
принадлежит плоскости тогда и только тогда, когда компланарны векторы 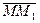 ,
,  и
и  , т.е. когда
, т.е. когда 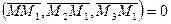 .
.
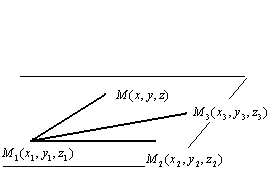
Поскольку 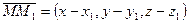 ,
, 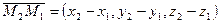 ,
, 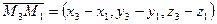 , записав смешанное произведение в координатной форме, имеем:
, записав смешанное произведение в координатной форме, имеем:
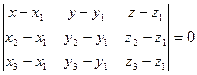 — уравнение плоскости, проходящей через три заданные точки.
— уравнение плоскости, проходящей через три заданные точки.
Преобразуем уравнение. Поскольку
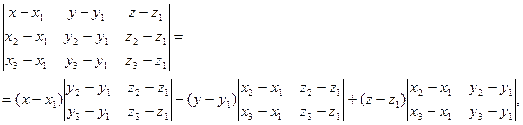
получим
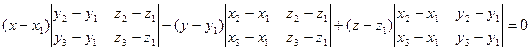 — линейное уравнение первой степени.
— линейное уравнение первой степени.
Заметим, что если заданные точки лежат на одной прямой, то векторы 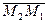 и
и 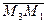 коллинеарны, т.е. все коэффициенты уравнения нулевые
коллинеарны, т.е. все коэффициенты уравнения нулевые 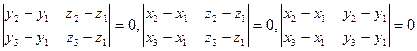 и вместо уравнения получим тождество 0 = 0.
и вместо уравнения получим тождество 0 = 0.
Нормальное уравнение плоскости. В уравнении 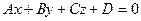 коэффициенты определяют нормальный вектор плоскости:
коэффициенты определяют нормальный вектор плоскости: 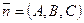 . Длина нормального вектора
. Длина нормального вектора 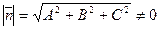 . Найдем орт нормального вектора плоскости:
. Найдем орт нормального вектора плоскости: 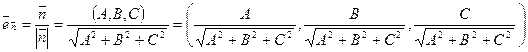 .
.
Легко видеть, что координаты орта вектора (орт — вектор единичной длины) равны косинусам углов, образованных этим ортом с положительными направлениями координатных осей:
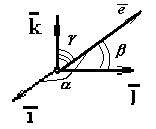
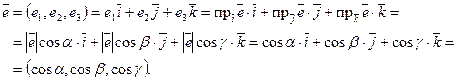
Здесь 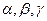 — углы, образованные ортом
— углы, образованные ортом 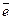 с положительными направлениями координатных осей. Косинусы этих углов называются направляющими косинусами вектора.
с положительными направлениями координатных осей. Косинусы этих углов называются направляющими косинусами вектора.
Т.е. координаты орта нормали к плоскости — направляющие косинусы нормали: 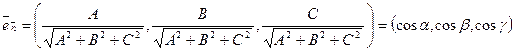 .
.
Здесь 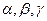 — углы, образованные нормалью к плоскостис положительными направлениями координатных осей.
— углы, образованные нормалью к плоскостис положительными направлениями координатных осей.
Разделив обе части уравнения 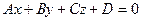 на
на 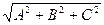 , получим
, получим 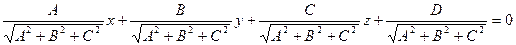 или, см. выше,
или, см. выше,
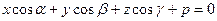 — нормальное уравнение плоскости,
— нормальное уравнение плоскости,
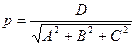 .
.
В нормальном уравнении плоскости коэффициенты при неизвестных — направляющие косинусы нормали, а свободный член p — измеряет расстояние от плоскости до начала координат. Действительно, если точка 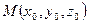 лежит на плоскости, то
лежит на плоскости, то 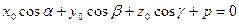 ; тогда
; тогда 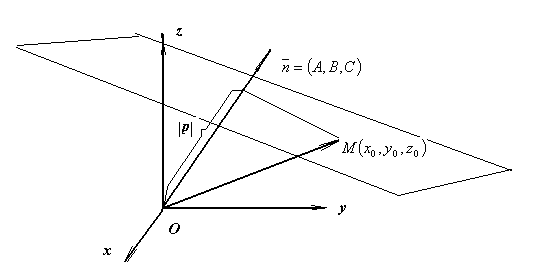
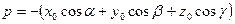 и
и 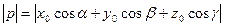 .
.
С другой стороны, расстояние от начала координат до плоскости равно, как легко видеть (см. рис.) 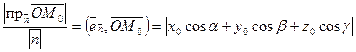 .
.
Угол между плоскостями. Угол между плоскостями равен углу между нормалями к плоскостям. Рассмотрим две плоскости, заданные уравнениями 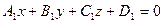 и
и 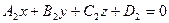 . Косинус угла между этими плоскостями легко вычислить:
. Косинус угла между этими плоскостями легко вычислить: 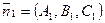 ,
,  ,
, 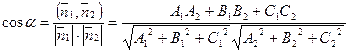 .
.
Здесь  — угол между плоскостями.
— угол между плоскостями.
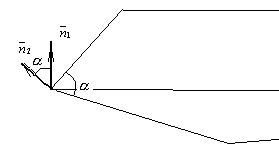
Расстояние между точкой и плоскостью.
Из приведенного рисунка видно, что расстояние от точки до плоскости равно разности длинны проекции радиуса вектора точки на орт нормали к плоскости и расстояния от начала координат до плоскости. 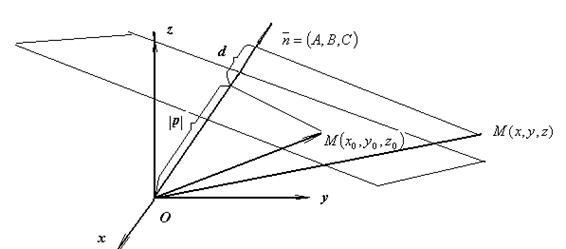
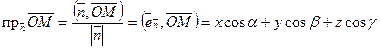 ,
, 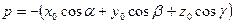 ,
,
тогда
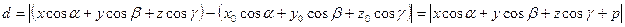 Итак, расстояние d от точки
Итак, расстояние d от точки 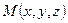 до плоскости
до плоскости 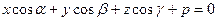
вычисляется по формуле 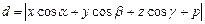 .
.
2. Уравнения прямой в пространстве
Общие уравнения прямой. Прямая в пространстве определяется как линия пересечения двух плоскостей. Рассмотрим две плоскости, заданные уравнениями 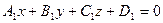 и
и  . Эти плоскости пересекаются, если их нормальные векторы не параллельны:
. Эти плоскости пересекаются, если их нормальные векторы не параллельны: 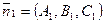 ,
,  ,
, 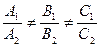 . Тогда координаты точек, принадлежащих обеим плоскостям — координаты точек прямой — удовлетворяют системе уравнений
. Тогда координаты точек, принадлежащих обеим плоскостям — координаты точек прямой — удовлетворяют системе уравнений
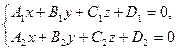 — общие уравнения прямой.
— общие уравнения прямой.
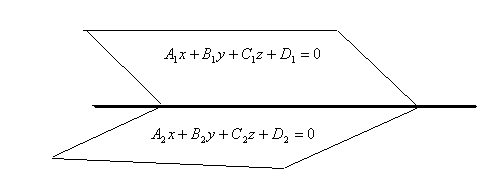
Уравнения прямой, проходящей через заданную точку параллельно заданному вектору. Пусть задана точка 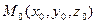 и вектор
и вектор 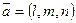 . Известно, что существует единственная прямая, проходящая через точку
. Известно, что существует единственная прямая, проходящая через точку 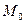 параллельно вектору
параллельно вектору  . Вектор
. Вектор  называется направляющим вектором прямой.
называется направляющим вектором прямой.
Как отличить точки принадлежащие прямой, от точек, которые этой прямой не принадлежат? Очевидно, что точка  принадлежит прямой тогда и только тогда, когда векторы
принадлежит прямой тогда и только тогда, когда векторы  и
и  коллинеарны, т.е. когда координаты этих векторов пропорциональны;
коллинеарны, т.е. когда координаты этих векторов пропорциональны;

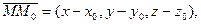
 ,
,
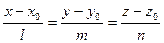 — канонические уравнения прямой, проходящей через заданную точку с заданным направляющим вектором.
— канонические уравнения прямой, проходящей через заданную точку с заданным направляющим вектором.
Уравнения прямой, проходящей через две заданные точки. Пусть заданы две точки 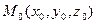 и
и  . Известно, что существует единственная прямая, проходящая через эти две точки.
. Известно, что существует единственная прямая, проходящая через эти две точки.
Как отличить точки принадлежащие прямой, от точек, которые этой прямой не принадлежат? Очевидно, что как м в предыдущей задаче, точка 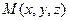 принадлежит прямой тогда и только тогда, когда векторы
принадлежит прямой тогда и только тогда, когда векторы  и
и  коллинеарны (в этом случае вектор
коллинеарны (в этом случае вектор 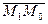 — направляющий вектор прямой) , т.е. когда координаты этих векторов пропорциональны;
— направляющий вектор прямой) , т.е. когда координаты этих векторов пропорциональны;
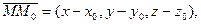

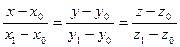 — канонические уравнения прямой, проходящей через две заданные точки.
— канонические уравнения прямой, проходящей через две заданные точки.
Параметрические уравнения прямой. Вернемся к каноническим уравнениям прямой: 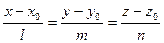 . Обозначим
. Обозначим 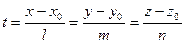 . Переменная t принимает все значения из
. Переменная t принимает все значения из  .
.
Тогда координаты точки  , принадлежащей прямой, удовлетворяют системе уравнений
, принадлежащей прямой, удовлетворяют системе уравнений
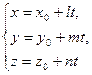 — параметрические уравнения прямой, проходящей через заданную точку с заданным направляющим вектором. Здесь
— параметрические уравнения прямой, проходящей через заданную точку с заданным направляющим вектором. Здесь 
Заметим, что при t =0 получим координаты точки 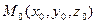 .
.
Связь различных видов уравнений прямой.
Общие уравнения прямой — система двух линейных уравнений первой степени относительно трех неизвестных.
Как записать общие уравнения прямой, если известны ее канонические уравнения?
Цепочка равенств 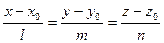 эквивалентна системе
эквивалентна системе
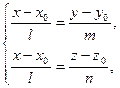
а это — система двух линейных уравнений первой степени относительно трех неизвестных, т.е. общие уравнения прямой.
Как записать общие уравнения прямой, если известны ее параметрические уравнения?
а это — система двух линейных уравнений первой степени относительно трех неизвестных, т.е. общие уравнения прямой.
Система 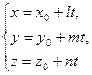 эквивалентна системе
эквивалентна системе 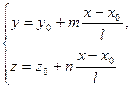 а это — система двух линейных уравнений первой степени относительно трех неизвестных, т.е. общие уравнения прямой.
а это — система двух линейных уравнений первой степени относительно трех неизвестных, т.е. общие уравнения прямой.
Как записать канонические уравнения прямой, если известны ее общие уравнения?
Для того чтобы записать канонические уравнения прямой, нужно найти направляющий вектор прямой и точку на прямой.
Если прямая задана общими уравнениями 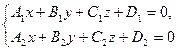 , то ее направляющий вектор ортогонален нормальным векторам обеих плоскостей:
, то ее направляющий вектор ортогонален нормальным векторам обеих плоскостей: 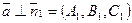 и
и  , т.е. направляющий вектор прямой можно вычислить как векторное произведение нормальных векторов:
, т.е. направляющий вектор прямой можно вычислить как векторное произведение нормальных векторов: 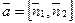 ,
, 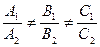 . Координаты точки на прямой можно найти как одно из множества решений системы
. Координаты точки на прямой можно найти как одно из множества решений системы  .
.
Когда точка и направляющий вектор найдены, можно записать канонические уравнения прямой.
3.Взаимное расположение прямой и плоскости
Параллельность прямой и плоскости. Прямая 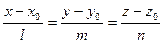 параллельна плоскости
параллельна плоскости 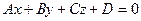 тогда и только тогда, когда направляющий вектор прямой
тогда и только тогда, когда направляющий вектор прямой  ортогонален нормальному вектору плоскости
ортогонален нормальному вектору плоскости 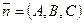 :
:
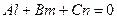 .
.
Прямая  параллельна плоскости
параллельна плоскости 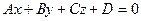 тогда и только тогда когда нормальные векторы
тогда и только тогда когда нормальные векторы 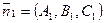 ,
, 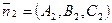 и
и 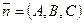 компланарны:
компланарны:
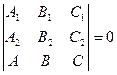 .
.
Пересечение прямой и плоскости. Если прямая и плоскость не параллельны, то они пересекаются. Точка пересечения прямой 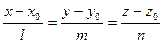 и плоскости
и плоскости 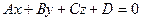 — решение системы
— решение системы
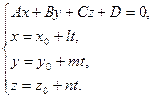
Точка пересечения прямой 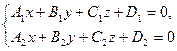 и плоскости
и плоскости 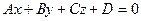 — решение системы
— решение системы 
4.Взаимное расположение прямых
Параллельность прямых. Прямая 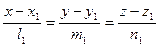 параллельна прямой
параллельна прямой  тогда и только тогда, когда их направляющие векторы коллинеарны:
тогда и только тогда, когда их направляющие векторы коллинеарны: 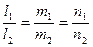 .
.
Расстояние от точки до прямой.
Из рисунка видно, что расстояние d от точки 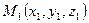 до прямой
до прямой  равно высоте параллелограмма, построенного на векторах
равно высоте параллелограмма, построенного на векторах  и
и  как на сторонах;
как на сторонах; 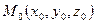 — точка на прямой.
— точка на прямой.
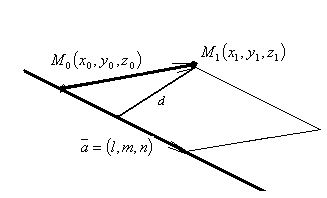
Тогда  .
.
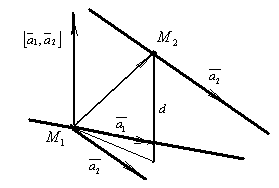
Расстояние между двумя непараллельными прямыми. Расстояние d между двумя непараллельными прямыми 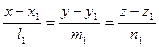 и
и 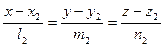 ,
, 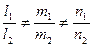 , равно проекции вектора
, равно проекции вектора 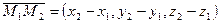 на общий перпендикуляр прямых.
на общий перпендикуляр прямых.
Общий перпендикуляр прямых коллинеарен векторному произведению их направляющих векторов: 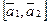 . А поскольку
. А поскольку 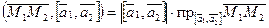 ,
, 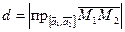 и
и 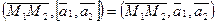 , то
, то 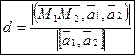 . Здесь
. Здесь 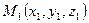 ,
, 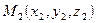 — точки на прямых,
— точки на прямых, 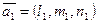 и
и 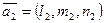 — направляющие векторы прямых.
— направляющие векторы прямых.
Лекция 3.Матрицы. Виды матриц. Операции над матрицами. Определитель n-го порядка. Обратная матрица
Прямоугольная таблица m · n чисел, расположенных в m строках и n столбцах называется прямоугольной ( m , n ) матрицей или просто матрицей.
Будем обозначать матрицы заглавными буквами — A, элементы матриц — 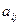 , столбцы матрицы —
, столбцы матрицы — 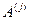 , а строки —
, а строки — 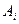 , транспонированная матрица —
, транспонированная матрица — 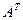 .
.
Некоторые часто встречающиеся виды матриц имеют собственные названия:
квадратная матрица, 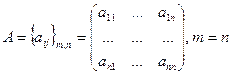 , матрица, у которой одинаковое число строк и столбцов;
, матрица, у которой одинаковое число строк и столбцов;
матрица-строка,  , матрица, у которой одна строка;
, матрица, у которой одна строка;
матрица-столбец, 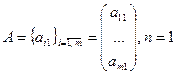 , матрица, у которой один столбец;
, матрица, у которой один столбец;
диагональная матрица, 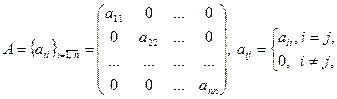 квадратная матрица, у которой все внедиагональные элементы раны нулю;
квадратная матрица, у которой все внедиагональные элементы раны нулю;
единичная матрица, 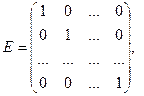 диагональная матрица, у которой все диагональные элементы — единицы нулю;
диагональная матрица, у которой все диагональные элементы — единицы нулю;
нулевая матрица,  , матрица, все элементы которой — нули;
, матрица, все элементы которой — нули;
верхняя треугольная матрица, 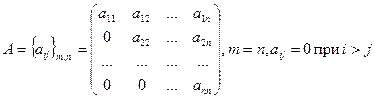 , квадратная матрица, у которой все элементы, расположенные ниже диагонали — нули;
, квадратная матрица, у которой все элементы, расположенные ниже диагонали — нули;
нижняя треугольная матрица, 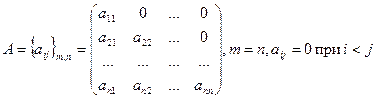 , квадратная матрица, у которой все элементы, расположенные выше диагонали — нули.
, квадратная матрица, у которой все элементы, расположенные выше диагонали — нули.
В дальнейшем важную роль будет играть ступенчатая матрица: 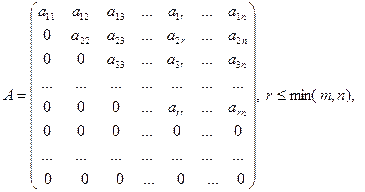 ,
,
т.е. существует такое число r, 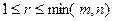 , что
, что 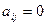 для всех
для всех 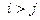 , и
, и 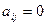 для всех при
для всех при 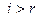 . Важно понимать, то у ступенчатой матрицы первые r диагональных элементов отличны от нуля:
. Важно понимать, то у ступенчатой матрицы первые r диагональных элементов отличны от нуля: 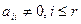 .
.
Определение. Две матрицы называются равными, если они имеют одинаковую размерность и равные соответственные элементы: 
Транспонирование матрицы
Для прямоугольных матриц определена операция транспонирования.
Определение. Рассмотрим произвольную прямоугольную матрицу A . Матрица, получающаяся из матрицы A заменой строк столбцами, называется транспонированной по отношению к матрице A и обозначается AT :
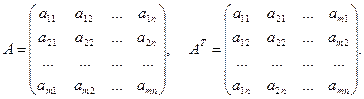
Линейные операции с матрицами. Линейными операциями называются операции сложения и умножения на число.
Определение. Суммой двух матриц одинаковой размерности называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых: 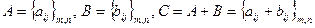 .
.
Определение. Произведением матрицы на число называется матрица той же размерности, каждый элемент которой равен произведению соответствующего элемента на число: 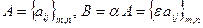 .
.
Для операций сложения и умножения матрицы на число справедливо:
1. A+B = B+A,
2. A+(B+C) = (A+B)+C,
3. α(A+B) = αA+αB,
4. α(β A) = (αβ)A,
5. (α+β)A=αA+βA,
6. 1·A=A,
7. 0·A= Q.
Здесь A, B, C — произвольные матрицы одинаковой размерности, Q — нулевая матрица той же размерности (читается «тэта»), a и b — произвольные числа.
Умножение матриц
Операция умножения матрицы на матрицу определяется более сложным образом.
Определение. Пусть заданы две матрицы A и B , причем число столбцов первой из них равно числу строк второй. Если
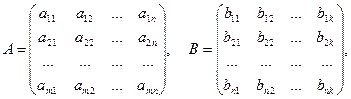
то произведением матриц A и B называется матрица
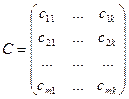 , элементы которой вычисляются по формуле
, элементы которой вычисляются по формуле
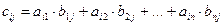 ,
, 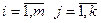 ; произведение матриц A и B обозначается AB: C= AB.
; произведение матриц A и B обозначается AB: C= AB.
Для произведения матриц соответствующих порядков справедливо:
1. A·B ≠ B·A,
2. (A + B) · C = A·C + B·C,
3. C·(A + B) = C·A + C·B,
4. α(A·B) = (αA) ·B,
5. (A·B) ·C = A·(B·C),
6. (AB)T = B TA T,
7. 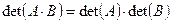 , A, B — квадратные матрицы одинаковой размерности.
, A, B — квадратные матрицы одинаковой размерности.
8. AE = EA = A, A— квадратная матрица, E — единичная матрица соответствующей размерности.
Если AB = BA, то матрицы A и B называются перестановочными.
Непосредственным вычислением легко проверить основное свойство единичной матрицы.
Определители
Для каждой квадратной матрицы определено число, называемое определителем матрицы, детерминантом матрицы или просто определителем (детерминантом).
Определение. Определителем квадратной матрицы первого порядка называется число, равное единственному элементу этой матрицы: A ={a}, detA =| A |= a .
Пусть A — произвольная квадратная матрица порядка n , n >1:
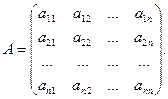
Определение Определителем n-го порядка (определителем квадратной матрицы n-го порядка n), n>1, называется число, равное
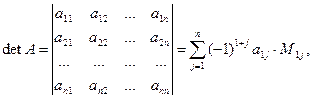
где  — определитель квадратной матрицы, полученной из матрицы A вычеркиванием первой строки и j-го столбца.
— определитель квадратной матрицы, полученной из матрицы A вычеркиванием первой строки и j-го столбца.
Для определителей 2-го и 3-го порядка легко получить простые выражения через элементы матрицы.
Определитель 2-го порядка:
 .
.
Определитель 3-го порядка:

Введем полезные в дальнейшем определения — минор элемента матрицы, алгебраическое дополнение элемента матрицы.
В этих новых терминах определение определителя n-го (n > 1) порядка звучит иначе.
Определение Определителем n-го порядка (определителем квадратной матрицы n-го порядка n), n>1, называется число, равное сумме произведений элементов первой строки на их алгебраические дополнения:
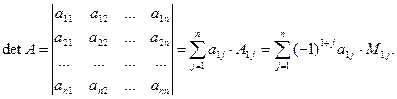
Справедливо следующее утверждение, которое мы не будем доказывать.
Теорема о вычислении определителя разложением по любой строке (столбцу). Определитель n -го порядка, n>1, равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.
Следствие. Определитель треугольной матрицы равен произведению диагональных элементов. (Доказать самостоятельно).
Свойства определителей
Для определителей справедливы следующие утверждения — свойства определителей.
1. Определитель не изменяется при транспонировании: det AT = det A.
2. При перестановке любых двух строк, определитель меняет знак.
3. Если в определителе есть две одинаковые строки, то он равен нулю.
4. Если все элементы строки определителя умножить на отличное от нуля число, то определитель умножается на это число: 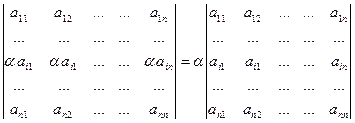 .
.
5. Если в определителе есть две пропорциональные строки, то он равен нулю.
6. Определитель, содержащий нулевую строку, равен нулю.
7. Если квадратные матрицы A, B и С отличаются только i -й строкой и при этом i -я строка а матрицы С равна сумме соответственных элементов i -х строк матриц A и B, то detC =detA + detB:
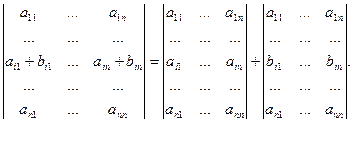
8. Определитель не изменится, если к элементам любой его строки прибавить элементы любой другой строки, умноженные на одно и то же число.
9. Сумма произведений элементов любой строки на алгебраические дополнения другой строки равна нулю: 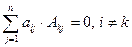 .
.
Поскольку определитель не меняется при транспонировании — утверждения 2—9 справедливы и для столбцов.
Перечисленные свойства позволяют упростить вычисление определителя.
Обратная матрица
Определение. Е сли существует квадратная матрица X той же размерности, что и матрица A, удовлетворяющая соотношениям A · X = X · A = E , то матрица A называется обратимой, а матрица X называется обратной к матрице A и обозначается A -1.
Здесь E — единичная матрица соответствующей размерности.Т.е. A · A -1= A -1· A = E .
Теорема о существовании обратной матрицы. Если 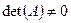 , то матрица A обратима и
, то матрица A обратима и
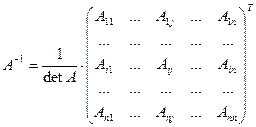 .
.
Здесь 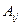 — алгебраическое дополнение элемента
— алгебраическое дополнение элемента 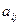 матрицы A .
матрицы A .
Доказательство теоремы. Докажем, что для матрицы 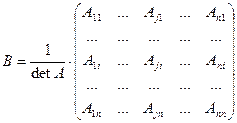 (транспонировали матрицу из алгебраических дополнений) справедливо:
(транспонировали матрицу из алгебраических дополнений) справедливо: 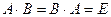 .
.
Вычислим 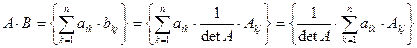 .
.
Если 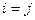 , то
, то 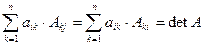 — сумма произведений элементов i-й строки матрицы A на их алгебраические дополнения. Если же Если
— сумма произведений элементов i-й строки матрицы A на их алгебраические дополнения. Если же Если 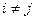 , то
, то 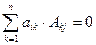 — сумма произведений элементов i-й строки матрицы A на алгебраические дополнения другой ( j-й строки,
— сумма произведений элементов i-й строки матрицы A на алгебраические дополнения другой ( j-й строки, 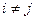 ). Отсюда следует, что диагональные (
). Отсюда следует, что диагональные ( 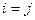 ) элементы матрицы
) элементы матрицы 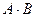 равны единице, а внедиагональные (
равны единице, а внедиагональные ( 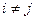 ) — равны нулю, т.е.
) — равны нулю, т.е. 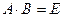 .
.
Равенство  доказывается совершенно аналогично. Докажите самостоятельно.
доказывается совершенно аналогично. Докажите самостоятельно.
Теорема (необходимое и достаточное условие существования обратной матрицы).
Для того, чтобы матрица A была обратима, необходимо и достаточно, чтобы 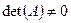 .
.
Доказательство теоремы. Необходимость. Дано: матрица A обратима. Докажем, что 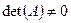 . Действительно, поскольку A — обратима, то
. Действительно, поскольку A — обратима, то 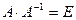 и
и 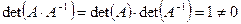 , и, следовательно,
, и, следовательно, 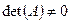 . Отсюда, в частности, следует, что окажем, что
. Отсюда, в частности, следует, что окажем, что 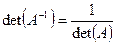 .
.
Достаточность. Дано: 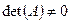 . Но тогда обратимость матрицы A следует из теоремы о существовании обратной матрицы. Теорема доказана.
. Но тогда обратимость матрицы A следует из теоремы о существовании обратной матрицы. Теорема доказана.
Теорема о единственности обратной матрицы. Обратная матрица единственна.
Доказательство. Докажем «от противного». Пусть это не так, и пусть 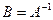 и
и  ,
, 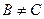 . Из определения обратной матрицы следует:
. Из определения обратной матрицы следует: 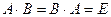 ,
, 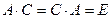 .
.
Тогда из ассоциативности умножения матриц и свойств единичной матрицы следует: Выполним некоторые вычисления:  , т.е.
, т.е.  . Противоречие с предположением
. Противоречие с предположением 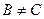 доказывает утверждение теоремы.
доказывает утверждение теоремы.
Аналогичными вычислениями можно доказать следующие свойства обратной матрицы:
-
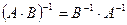 .
. -
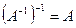 .
.
Действительно:
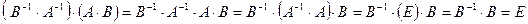 , и
, и
совершенно аналогично, 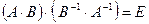 , т.е.
, т.е. 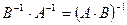 .
.
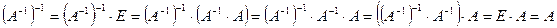 .
.
Нетрудно также доказать, что матрица, обратная к диагональной матрице — диагональная, обратная к треугольной — треугольная, обратная к симметричной матрице — симметрична. Докажите эти утверждения самостоятельно.
Ниже приведен порядок операций при вычислении обратной матрицы.

Матричная запись системы линейных алгебраических уравнений. Рассмотрим систему линейных алгебраических уравнений
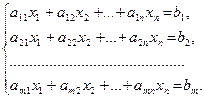
Обозначим: 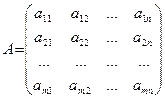 ,
, 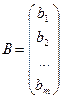 ,
,  ,
,
A — матрица системы, B — правая часть, X — матрица-столбец неизвестных.
Тогда:
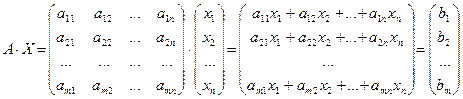 тогда и только тогда, когда для элементов матрицы X справедливы равенства рассмотренной системы. Т.е. система эквивалентна матричному уравнению A· X = B, в том смысле, что если числа
тогда и только тогда, когда для элементов матрицы X справедливы равенства рассмотренной системы. Т.е. система эквивалентна матричному уравнению A· X = B, в том смысле, что если числа 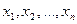 являются решением рассмотренной системы, то соответствующая матрица X является решением матричного уравнения; и наоборот, если матрица X является решением матричного уравнения, то ее элементы
являются решением рассмотренной системы, то соответствующая матрица X является решением матричного уравнения; и наоборот, если матрица X является решением матричного уравнения, то ее элементы 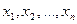 являются решением рассмотренной системы.
являются решением рассмотренной системы.
Матричные уравнения. Рассмотрим матричное уравнение A · X = B.
Если m = n и матрица A обратима, то
 ,
,
т.е. получили выражение для решения системы матричного уравнения
A · X = B. Ясно, что по этой формуле можно вычислить решение системы n линейных алгебраических уравнений относительно n неизвестных (см. запись системы в матричной форме).
Аналогично, если соответствующие матрицы обратимы, имеем:
X·A = B, X = B·A-1,
A·X·B = C, X = A-1·C· B-1,
A·X+B = 0, A·X = - B, X = - A-1·B.
Формулы Крамера. Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных
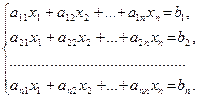
Обозначим:  — определитель матрицы системы, и
— определитель матрицы системы, и 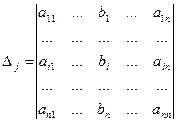 — определитель матрицы, полученной из матрицы системы заменой j-го столбца столбцом правых частей.
— определитель матрицы, полученной из матрицы системы заменой j-го столбца столбцом правых частей.
Если определитель матрицы системы отличен от нуля, 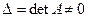 , то решение системы
, то решение системы
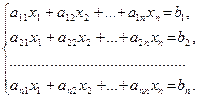
определяется равенствами: 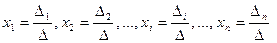 .
.
Докажем это утверждение. Пусть 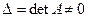 .
.
Обозначим  и покажем, что
и покажем, что 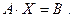 Вычислим
Вычислим

Вычислим определитель 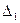 разложением по первому столбцу, определитель
разложением по первому столбцу, определитель  — по второму, …,
— по второму, …, 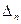 — по n-му:
— по n-му:
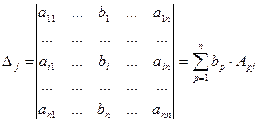 , поскольку определитель
, поскольку определитель 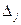 отличается от
отличается от  только j-м столбцом.
только j-м столбцом.
Тогда
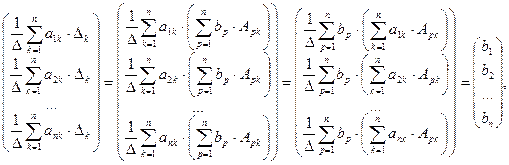
поскольку
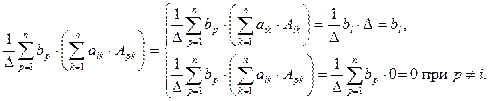
Т.е. 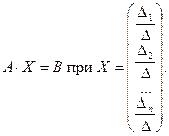 Формулы Крамера доказаны.
Формулы Крамера доказаны.
Замечание. Нетрудно, показать, что выражения 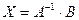 и
и 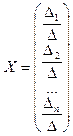 — две формы записи одного и того же равенства.
— две формы записи одного и того же равенства.
Действительно,
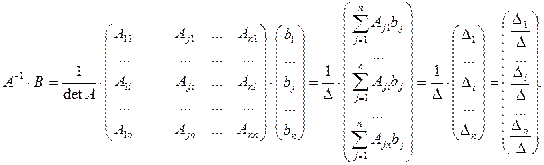
Вычисление обратной матрицы методом Гаусса-Жордана
Пусть A — обратимая квадратная матрица. Обозначим 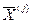 — j -й столбец обратной матрицы. Тогда, поскольку A ∙ A-1=E, то, очевидно, справедливо:
— j -й столбец обратной матрицы. Тогда, поскольку A ∙ A-1=E, то, очевидно, справедливо:

т.е. 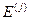 — матрица-столбец, все элементы которой, кроме j-го равны нулю, а элемент, расположенный в j-й строке равен единице.
— матрица-столбец, все элементы которой, кроме j-го равны нулю, а элемент, расположенный в j-й строке равен единице.
Эти n систем можно решать методом Гаусса-Жордана одновременно, поскольку у всех у них одна и та же матрица. Запишем матрицу, содержащую в первых n столбцах матрицу системы, а в последних n столбцах — единичную матрицу, и выполним Гауссово исключение так, чтобы получилось:
Матрица, расположенная в последних n столбцах — обратная матрица. Действительно, в (n+1)-м столбце — решение системы  , т.е. первый столбец обратной матрицы, в (n+2)-м столбце — решение системы
, т.е. первый столбец обратной матрицы, в (n+2)-м столбце — решение системы 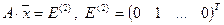 , т.е. второй столбец обратной матрицы, и т.д., в (n+ n)-м столбце — решение системы
, т.е. второй столбец обратной матрицы, и т.д., в (n+ n)-м столбце — решение системы 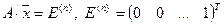 , т.е. n -й столбец обратной матрицы.
, т.е. n -й столбец обратной матрицы.
Лекция 4. Приведение матрицы к ступенчатому виду. Ранг матрицы. Однородные системы линейных алгебраических уравнений. Фундаментальная система решений Структура общего решения. Условие нетривиальной совместности
Элементарные преобразования матриц
Помимо операций с матрицами определены операции с элементами матриц, операции со столбцами и строками матрицы — так называемые элементарные преобразования матриц.
Определение. Элементарными преобразованиями матрицы называют следующие операции:
1. перестановка любых двух строк (столбцов) матрицы;
2. умножение любой строки (столбца) на произвольное, отличное от нуля, число;
3. сложение любой строки (столбца) с другой строкой (столбцом), умноженной (умноженным) на произвольное, отличное от нуля, число.
4. к элементарным преобразованиям иногда относят и операцию транспонирования матрицы.
Приведение матрицы к ступенчатому виду Гауссовым исключением
Утверждение. Любую прямоугольную матрицу можно с помощью элементарных преобразований привести к ступенчатой форме.
Это утверждение на лекции доказано.
Алгоритм приведения матрицы к ступенчатой форме с помощью элементарных преобразований называют Гауссовым исключением или методом Гаусса.
Ранг матрицы
Определение. Ранг матрицы равен максимальному числу линейно независимых строк матрицы. Обозначаем RgA , rgA.
Т.е., если ранг матрицы равен r, то среди строк матрицы есть r линейно независимых строк, а любые r +1 строки — линейно зависимы.
Определение. Матрицы, имеющие одинаковый ранг, называются подобными.
Утверждение. Элементарные преобразования не меняют ранга матрицы.
Доказательство утверждения. Пусть Am , n — прямоугольная матрица и RgA = r. Не умаляя общности, положим — линейно независимы первые r строк: 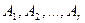 . Выполним элементарные преобразования строк матрицы. Обозначим полученную матрицу A ’, ее строки —
. Выполним элементарные преобразования строк матрицы. Обозначим полученную матрицу A ’, ее строки — 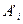 .Очевидно, что перестановка строк или умножение строки на число не может повлиять на количество линейно независимых строк.
.Очевидно, что перестановка строк или умножение строки на число не может повлиять на количество линейно независимых строк.
Выполним такое преобразование: к одной из строк матрицы прибавим другую, умноженную на отличное от нуля число.
Сначала выполним такое преобразование с первыми r линейно независимыми строками.
Например, 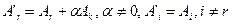 . Тогда
. Тогда 
Т.к. строки 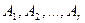 , то линейная комбинация равна нулю тогда и только тогда, когда
, то линейная комбинация равна нулю тогда и только тогда, когда 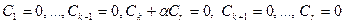 . Отсюда немедленно следует, что и
. Отсюда немедленно следует, что и  , т.е. первые r строк преобразованной матрицы
, т.е. первые r строк преобразованной матрицы 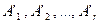 — линейно независимы. Покажем, что любая система
— линейно независимы. Покажем, что любая система 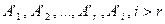 строк преобразованной матрицы линейно зависима, т.е. покажем, что строка
строк преобразованной матрицы линейно зависима, т.е. покажем, что строка 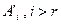 линейно выражается через строки
линейно выражается через строки 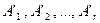 :
:
поскольку строки 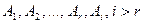 линейно зависимы, то
линейно зависимы, то
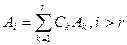 , а отсюда —
, а отсюда — 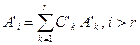 и
и

Если же 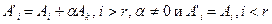 , то первые r строк преобразованной матрицы линейно независимы, а любые r +1 линейно зависимы, т.к. любая строка преобразованной матрицы линейно выражается через ее первые r линейно независимых строк:
, то первые r строк преобразованной матрицы линейно независимы, а любые r +1 линейно зависимы, т.к. любая строка преобразованной матрицы линейно выражается через ее первые r линейно независимых строк:
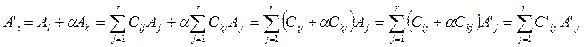
Утверждение доказано.
Теорема. Ранг матрицы равен числу ненулевых строк в ступенчатой форме матрицы.
Доказательство теоремы. Рассмотрим ступенчатую матрицу
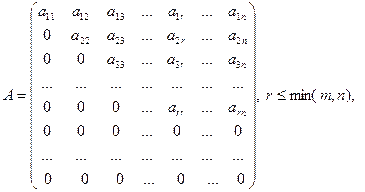
т.е. 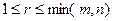 ,
, 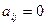 для всех
для всех 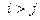 , и
, и 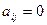 для всех при
для всех при 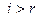 . Важно понимать, то у ступенчатой матрицы первые r диагональных элементов отличны от нуля:
. Важно понимать, то у ступенчатой матрицы первые r диагональных элементов отличны от нуля: 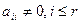 .
.
Первые r строк этой матрицы линейно независимы. Действительно, приравняем к нулю линейную комбинацию этих строк: 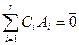 и вычислим ее в естественном базисе:
и вычислим ее в естественном базисе:
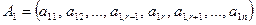 ,
,
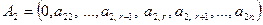 , …,
, …,
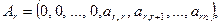

Равенство нулю линейной комбинации возможно тогда и только тогда, когда:
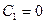 , поскольку
, поскольку 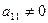 ,
,
 , поскольку
, поскольку 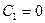 и
и 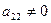 , …,
, …,
 , поскольку
, поскольку 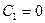 ,
, 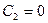 , …,
, …, 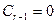 и
и  .
.
Итак, первые r ненулевые строки линейно независимы, а любые r+1 строки — линейно зависимы, т.к. линейно зависима любая система векторов, содержащая нулевой вектор.
Теорема доказана.
Отсюда — алгоритм вычисления ранга матрицы.
Приведем матрицу к ступенчатому виду (доказано, что это можно сделать гауссовым исключением), ранг исследуемой матрицы равен рангу ступенчатой матрицы (выше доказано, что элементарные преобразования не меняют ранга матрицы) , ранг ступенчатой матрицы равен числу ненулевых строк в ступенчатой форме матрицы (по только что доказанной теореме).
Системы линейных алгебраических уравнений. Основные понятия
Рассмотрим систему m линейных алгебраических уравнений относительно n неизвестных 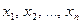 :
:

Определение. Решением системы называется совокупность n значений неизвестных  , при подстановке которых
, при подстановке которых 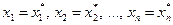 все уравнения системы обращаются в тождества.
все уравнения системы обращаются в тождества.
Определение. Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.
Напомним, что система линейных уравнений может быть записана в матричной форме:
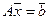 ,
,
где 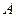 — матрица системы,
— матрица системы, 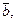 — правая часть,
— правая часть, 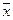 — искомое решение,
— искомое решение,
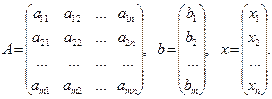
Иногда удобно записывать систему линейных уравнений в другой матричной форме:
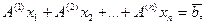
где 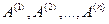 — столбцы матрицы системы.
— столбцы матрицы системы.
Обозначим 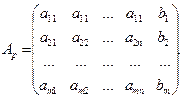
Матрица 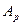 называется расширенной матрицей системы.
называется расширенной матрицей системы.
Определение. Если правая часть системы равна нулю, то система называется однородной.
Определение. Для системы 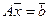 однородная система
однородная система 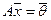 (с той же матрицей системы A) называется приведенной однородной системой.
(с той же матрицей системы A) называется приведенной однородной системой.
Дата: 2019-02-02, просмотров: 381.