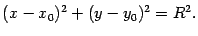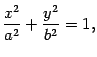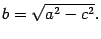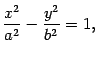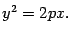Лекция 4. Приведение матрицы к ступенчатому виду. Ранг матрицы. Однородные системы линейных алгебраических уравнений. Фундаментальная система решений Структура общего решения. Условие нетривиальной совместности
Элементарные преобразования матриц
Помимо операций с матрицами определены операции с элементами матриц, операции со столбцами и строками матрицы — так называемые элементарные преобразования матриц.
Определение. Элементарными преобразованиями матрицы называют следующие операции:
1. перестановка любых двух строк (столбцов) матрицы;
2. умножение любой строки (столбца) на произвольное, отличное от нуля, число;
3. сложение любой строки (столбца) с другой строкой (столбцом), умноженной (умноженным) на произвольное, отличное от нуля, число.
4. к элементарным преобразованиям иногда относят и операцию транспонирования матрицы.
Приведение матрицы к ступенчатому виду Гауссовым исключением
Утверждение. Любую прямоугольную матрицу можно с помощью элементарных преобразований привести к ступенчатой форме.
Это утверждение на лекции доказано.
Алгоритм приведения матрицы к ступенчатой форме с помощью элементарных преобразований называют Гауссовым исключением или методом Гаусса.
Ранг матрицы
Определение. Ранг матрицы равен максимальному числу линейно независимых строк матрицы. Обозначаем RgA , rgA.
Т.е., если ранг матрицы равен r, то среди строк матрицы есть r линейно независимых строк, а любые r +1 строки — линейно зависимы.
Определение. Матрицы, имеющие одинаковый ранг, называются подобными.
Утверждение. Элементарные преобразования не меняют ранга матрицы.
Доказательство утверждения. Пусть Am , n — прямоугольная матрица и RgA = r. Не умаляя общности, положим — линейно независимы первые r строк:  . Выполним элементарные преобразования строк матрицы. Обозначим полученную матрицу A ’, ее строки —
. Выполним элементарные преобразования строк матрицы. Обозначим полученную матрицу A ’, ее строки —  .Очевидно, что перестановка строк или умножение строки на число не может повлиять на количество линейно независимых строк.
.Очевидно, что перестановка строк или умножение строки на число не может повлиять на количество линейно независимых строк.
Выполним такое преобразование: к одной из строк матрицы прибавим другую, умноженную на отличное от нуля число.
Сначала выполним такое преобразование с первыми r линейно независимыми строками.
Например,  . Тогда
. Тогда 
Т.к. строки 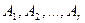 , то линейная комбинация равна нулю тогда и только тогда, когда
, то линейная комбинация равна нулю тогда и только тогда, когда 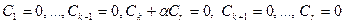 . Отсюда немедленно следует, что и
. Отсюда немедленно следует, что и  , т.е. первые r строк преобразованной матрицы
, т.е. первые r строк преобразованной матрицы 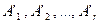 — линейно независимы. Покажем, что любая система
— линейно независимы. Покажем, что любая система 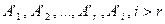 строк преобразованной матрицы линейно зависима, т.е. покажем, что строка
строк преобразованной матрицы линейно зависима, т.е. покажем, что строка 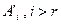 линейно выражается через строки
линейно выражается через строки 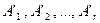 :
:
поскольку строки 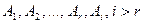 линейно зависимы, то
линейно зависимы, то
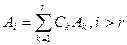 , а отсюда —
, а отсюда — 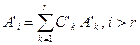 и
и

Если же 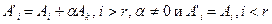 , то первые r строк преобразованной матрицы линейно независимы, а любые r +1 линейно зависимы, т.к. любая строка преобразованной матрицы линейно выражается через ее первые r линейно независимых строк:
, то первые r строк преобразованной матрицы линейно независимы, а любые r +1 линейно зависимы, т.к. любая строка преобразованной матрицы линейно выражается через ее первые r линейно независимых строк:
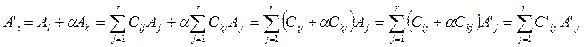
Утверждение доказано.
Теорема. Ранг матрицы равен числу ненулевых строк в ступенчатой форме матрицы.
Доказательство теоремы. Рассмотрим ступенчатую матрицу
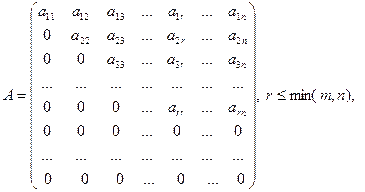
т.е. 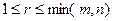 ,
, 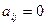 для всех
для всех 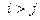 , и
, и 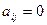 для всех при
для всех при 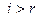 . Важно понимать, то у ступенчатой матрицы первые r диагональных элементов отличны от нуля:
. Важно понимать, то у ступенчатой матрицы первые r диагональных элементов отличны от нуля: 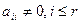 .
.
Первые r строк этой матрицы линейно независимы. Действительно, приравняем к нулю линейную комбинацию этих строк: 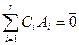 и вычислим ее в естественном базисе:
и вычислим ее в естественном базисе:
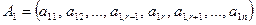 ,
,
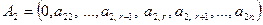 , …,
, …,
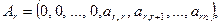

Равенство нулю линейной комбинации возможно тогда и только тогда, когда:
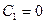 , поскольку
, поскольку 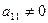 ,
,
 , поскольку
, поскольку 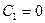 и
и 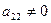 , …,
, …,
 , поскольку
, поскольку 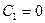 ,
, 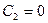 , …,
, …, 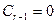 и
и  .
.
Итак, первые r ненулевые строки линейно независимы, а любые r+1 строки — линейно зависимы, т.к. линейно зависима любая система векторов, содержащая нулевой вектор.
Теорема доказана.
Отсюда — алгоритм вычисления ранга матрицы.
Приведем матрицу к ступенчатому виду (доказано, что это можно сделать гауссовым исключением), ранг исследуемой матрицы равен рангу ступенчатой матрицы (выше доказано, что элементарные преобразования не меняют ранга матрицы) , ранг ступенчатой матрицы равен числу ненулевых строк в ступенчатой форме матрицы (по только что доказанной теореме).
Системы линейных алгебраических уравнений. Основные понятия
Рассмотрим систему m линейных алгебраических уравнений относительно n неизвестных 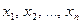 :
:

Определение. Решением системы называется совокупность n значений неизвестных  , при подстановке которых
, при подстановке которых 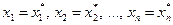 все уравнения системы обращаются в тождества.
все уравнения системы обращаются в тождества.
Определение. Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.
Напомним, что система линейных уравнений может быть записана в матричной форме:
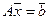 ,
,
где 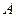 — матрица системы,
— матрица системы, 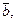 — правая часть,
— правая часть, 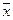 — искомое решение,
— искомое решение,
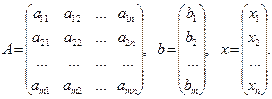
Иногда удобно записывать систему линейных уравнений в другой матричной форме:
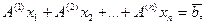
где 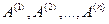 — столбцы матрицы системы.
— столбцы матрицы системы.
Обозначим 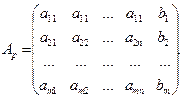
Матрица 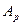 называется расширенной матрицей системы.
называется расширенной матрицей системы.
Определение. Если правая часть системы равна нулю, то система называется однородной.
Определение. Для системы 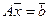 однородная система
однородная система 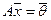 (с той же матрицей системы A) называется приведенной однородной системой.
(с той же матрицей системы A) называется приведенной однородной системой.
Пример.
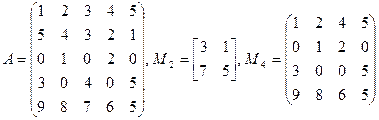
минор M 2 расположен на пересечении 2-й и 5-й строк с 3-м и 5-м столбцами, а минор M 4 — на пересечении 1-й, 3-й, 4-й и 5-й строк с 1-м, 2-м, 4-м и 5-м столбцами.
Минор Mr, расположенный в первых r строках и в первых r столбцах матрицы , называется угловым или главным минором матрицы.
Справедлива следующая теорема.
Теорема о базисном миноре. Если ранг матрицы равен r , то у матрицы есть отличный от нуля минор порядка r. Строки и столбцы этого минора линейно независимы, а все остальные строки и столбцы матрицы через них линейно выражаются.
Доказательство теоремы опускаем. Его можно найти в учебниках, приведенных в списке литературы.
Отличный от нуля минор r-го порядка матрицы, ранг которой равен r, называется базисным минором, столбцы матрицы, входящие в этот минор называются базисными столбцами, а строки, входящие в базисный минор — базисными строками.
Т.е. теорема о базисном миноре утверждает, что базисные строки и базисные столбцы матрицы линейно независимы, а остальные строки и столбцы матрицы линейно выражаются через базисные.
Следствия из теоремы о базисном миноре
1. Если ранг матрицы равен r, то все миноры матрицы более высокого порядка равны нулю.
Действительно. Любой минор более высокого порядка содержит хотя бы один столбец (строку), который линейно выражается через столбцы базисного минора, и, следовательно, равен нулю, поскольку разлагается в линейную комбинацию определителей с хотя бы двумя равными столбцами:
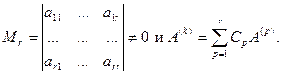
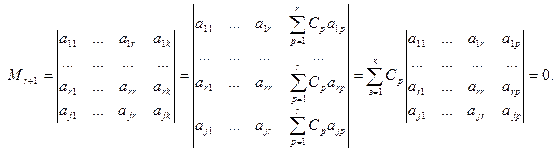
2. Ранг матрицы равен наивысшему порядку отличных от нуля миноров матрицы.
Действительно, из теоремы о базисном миноре следует, размерность базисного минора — наибольшее число линейно независимых строк (столбцов) матрицы.
3. Строки и столбцы квадратной матрицы линейно независимы тогда и только тогда, когда ее определитель отличен от нуля.
Действительно, определитель — минор наивысшего порядка. Если он отличен от нуля, то он и есть базисный минор матрицы, т.е. все его столбцы (строки) — базисные — линейно независимые. И наоборот. Если все n строк и столбцов квадратной матрицы порядка n линейно независимы, то ранг матрицы равен n. Но по теореме о базисном миноре существует отличный от нуля минор матрицы порядка n, а такой минор — определитель матрицы.
Замечание. Утверждение теоремы о базисном миноре легко понять на примере ступенчатой матрицы. Вспомним, что ранг ступенчатой матрицы 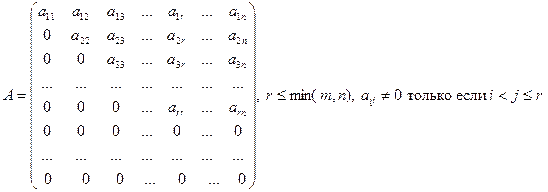
равен числу r ненулевых строк. Видно, что главный минор этой матрицы, Mr отличен от нуля:
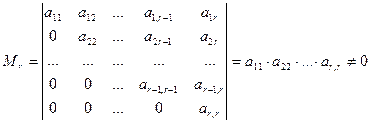
ведь все диагональные элементы  отличны от нуля.
отличны от нуля.
Любой минор более высокого порядка содержит нулевую строку, т.е. равен нулю.
Нетривиальная совместность однородных систем. Необходимое и достаточное условие нетривиальной совместности однородной системы
Мы уже говорили, что однородная система линейных алгебраических уравнений всегда совместна. Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди этих решений есть и ненулевые и в этом случае система называется нетривиально совместной.
Пример. Вектор 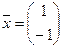 — отличное от нуля решение однородной системы
— отличное от нуля решение однородной системы 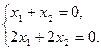
Теорема (необходимое и достаточное условие нетривиальной совместности однородной системы). Для того чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных.
Доказательство теоремы
Необходимость. Система  нетривиально совместна. Это означает, что существуют числа
нетривиально совместна. Это означает, что существуют числа 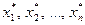 не все равные нулю, для которых справедливо
не все равные нулю, для которых справедливо 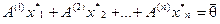 . Последнее равенство означает, что n столбцов матрицы систем линейно зависимы и, следовательно, ранг матрицы системы (максимальное число линейно независимых столбцов) меньше числа столбцов, меньше числа неизвестных. Необходимость доказана.
. Последнее равенство означает, что n столбцов матрицы систем линейно зависимы и, следовательно, ранг матрицы системы (максимальное число линейно независимых столбцов) меньше числа столбцов, меньше числа неизвестных. Необходимость доказана.
Достаточность. Пусть ранг r матрицы системы меньше числа n неизвестных. По теореме о базисном миноре из этого следует, что существует отличный от нуля минор матрицы порядка r. Не умаляя общности, будем полагать, что базисный минор — главный минор матрицы 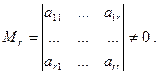
Рассмотрим первые r уравнений системы (по теореме о базисном миноре остальные уравнения — линейные комбинации этих первых уравнений):
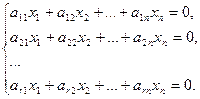
Оставим слева первые r неизвестных, а остальные n - r неизвестные перенесем вправо и получим неоднородную систему линейных уравнений относительно неизвестных 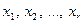 :
:

Определитель полученной системы — отличный от нуля базисный минор Mr.
Уравнения системы справедливы при произвольных значениях переменных 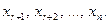 Их естественно называть свободными. А переменные
Их естественно называть свободными. А переменные 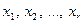 в левой части уравнений системы естественно назвать базисными.
в левой части уравнений системы естественно назвать базисными.
Базисные переменные можно вычислить по формулам Крамера 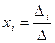 , i = 1, 2, …, r . Здесь
, i = 1, 2, …, r . Здесь 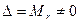 — определитель матрицы системы, а
— определитель матрицы системы, а 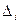 — определитель, полученный из Mr заменой i -го столбцом правых частей. Вычислим, например, x1.
— определитель, полученный из Mr заменой i -го столбцом правых частей. Вычислим, например, x1.

Здесь 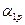 — некоторые числа.
— некоторые числа.
Итак, 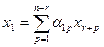 . Аналогично
. Аналогично 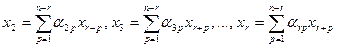 — т.е. базисные переменные линейно выражаются через свободные переменные.
— т.е. базисные переменные линейно выражаются через свободные переменные.
Положим, например такие значения свободных переменных: 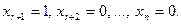
Тогда вектор 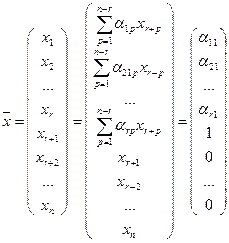 — отличное от тождественного нуля решение однородной системы
— отличное от тождественного нуля решение однородной системы  . Т.е. однородная система нетривиально совместна. Теорема доказана.
. Т.е. однородная система нетривиально совместна. Теорема доказана.
Фундаментальная система решений однородной системы. Структура общего решения однородной системы
Вспомним, что решения однородной системы 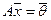 — векторы из Rn. Вспомним также, что в силу свойств решений линейной однородной системы множество L ее решений — линейное подпространство в Rn. Действительно: если
— векторы из Rn. Вспомним также, что в силу свойств решений линейной однородной системы множество L ее решений — линейное подпространство в Rn. Действительно: если 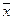 и
и 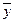 — два решения однородной системы
— два решения однородной системы 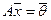 , то при любых действительных числах α и β вектор
, то при любых действительных числах α и β вектор 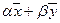 — решение системы
— решение системы 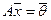 , иначе говоря, для любых
, иначе говоря, для любых  и
и  и любого числах α
и любого числах α 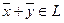 и
и 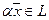 . Доказано также, что если ранг r матрицы системы меньше числа неизвестных n, то система имеет ненулевые решения.
. Доказано также, что если ранг r матрицы системы меньше числа неизвестных n, то система имеет ненулевые решения.
Определение. Выражение, позволяющее вычислить все (любое) решения системы, называется общим решением системы.
В теореме о нетривиальной совместности однородной системы показано, что если r — ранг матрицы системы, то r базисных переменных выражаются через свободные переменные по формулам
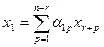 ,
, 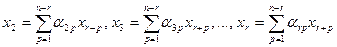 .
.
Здесь для простоты полагали, что базисные переменные — это первые r переменных. Вообще говоря, это могут быть любые r переменных.
Итак, 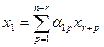 ,
,  — т.е. базисные переменные линейно выражаются через свободные переменные.
— т.е. базисные переменные линейно выражаются через свободные переменные.
Построим n - r ненулевых решений однородной системы специальным образом.
Сначала положим 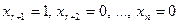 и полученное решение обозначим
и полученное решение обозначим 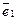 .
.
Затем положим 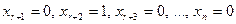 и полученное решение обозначим
и полученное решение обозначим 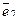 ,
,
и т.д., и, наконец, положим 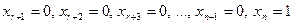 и полученное решение обозначим
и полученное решение обозначим 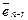 . Имеем (см. док-во теоремы о нетривиальной совместности)
. Имеем (см. док-во теоремы о нетривиальной совместности)
 .
.
Нетрудно видеть, что эти n - r ненулевые решения линейно независимы.
Действительно, запишем матрицу, столбцами которой являются векторы 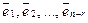 :
:
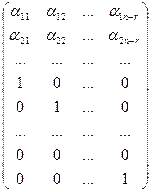 .
.
Минор этой матрицы, расположенный в последних n - r строках равен 1, отличен от нуля. Это означает, что ранг матрицы равен n - r и что ее n - r столбца линейно независимы. А столбцы этой матрицы — ненулевые решения однородной системы 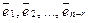 .
.
С другой стороны, любое решение системы, в соответствии с приведенными выше формулами, можно записать в виде:
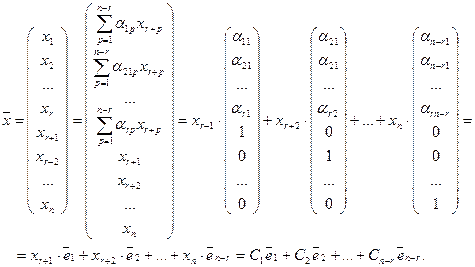
Здесь произвольные значения свободных переменных 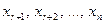 обозначены буквами
обозначены буквами 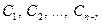 .
.
Подведем итог:
ü построена система 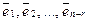 , состоящая из n - r линейно независимых решений однородной системы;
, состоящая из n - r линейно независимых решений однородной системы;
ü любое решение системы линейно выражается через решения 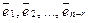 ;
;
ü множество решений однородной системы — линейное подпространство.
Тогда можно утверждать:
1. размерность подпространства L решений однородной системы 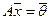 равна n – r , где n — число неизвестных, r = RgA: dimL = n – r;
равна n – r , где n — число неизвестных, r = RgA: dimL = n – r;
2. система 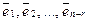 — базис в подпространстве L решений однородной системы
— базис в подпространстве L решений однородной системы 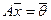 ;
;
3. выражение  — общее решение однородной системы.
— общее решение однородной системы.
Определение. Система 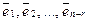 , состоящая из n - r линейно независимых решений однородной системы
, состоящая из n - r линейно независимых решений однородной системы 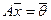 ,
, 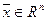 , RgA = r , называется фундаментальной системой решений однородной системы.
, RgA = r , называется фундаментальной системой решений однородной системы.
Выше мы доказали следующие утверждения.
Утверждение. Фундаментальная система решений однородной системы — базис пространства решений однородной системы.
Теорема о структуре общего решения однородной системы линейных алгебраических уравнений. Если ранг r матрицы однородной системы линейных уравнений меньше числа неизвестных n , то общее решение системы можно записать в виде линейной комбинации решений фундаментальной системы:  .
.
Доказательство теоремы.
Необходимость. Система  совместна. Докажем, что
совместна. Докажем, что  .
.
Система  совместна — существуют такие числа
совместна — существуют такие числа  , что
, что
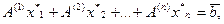
т.е. вектор-столбец правой части линейно выражается через столбцы 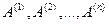 матрицы A. Это означает, что при добавлении столбца
матрицы A. Это означает, что при добавлении столбца 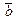 число линейно независимых столбцов не увеличивается, т.е.
число линейно независимых столбцов не увеличивается, т.е.  . Необходимость доказана.
. Необходимость доказана.
Достаточность. 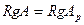 . Докажем, что система
. Докажем, что система 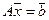 совместна.
совместна.
Пусть 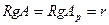 . Это означает, что среди столбцов обеих матриц есть r линейно независимых столбцов, а все остальные линейно выражаются через эти r столбцов. Не умаляя общности, положим, что линейно независимы первые r столбцов
. Это означает, что среди столбцов обеих матриц есть r линейно независимых столбцов, а все остальные линейно выражаются через эти r столбцов. Не умаляя общности, положим, что линейно независимы первые r столбцов 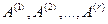 . Тогда столбцы
. Тогда столбцы 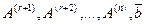 — линейно зависимы и, следовательно, столбец
— линейно зависимы и, следовательно, столбец  линейно выражается через
линейно выражается через 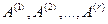 :
: 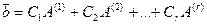 .
.
Положим 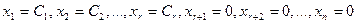 ,
,
тогда

т.е. вектор 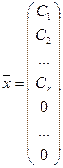 — решение системы
— решение системы  ,
,
т.е. система 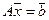 совместна. Теорема доказана.
совместна. Теорема доказана.
Свойства решений систем линейных алгебраических уравнений
Используя свойства линейных операций с матрицами, нетрудно доказать, справедливость следующих утверждений.
1. Если  и
и 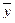 — два решения однородной системы
— два решения однородной системы 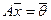 , то при любых действительных числах α и β вектор
, то при любых действительных числах α и β вектор 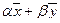 — решение системы
— решение системы 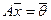 .
.
2. Если  и
и 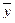 — два решения неоднородной системы
— два решения неоднородной системы  , то вектор
, то вектор 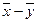 — решение приведенной однородной системы однородной
— решение приведенной однородной системы однородной 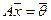 .
.
3. Если  решение неоднородной системы
решение неоднородной системы  , а
, а 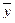 — решение однородной системы
— решение однородной системы 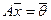 , то вектор
, то вектор  — решение неоднородной системы
— решение неоднородной системы  .
.
Докажем, например, первое из этих свойств. Пусть  и
и 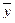 — два решения системы
— два решения системы 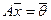 , т. е.
, т. е. 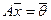 и
и 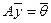 и пусть α и β любые действительные числа. Тогда
и пусть α и β любые действительные числа. Тогда 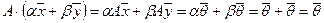 , т.е. вектор
, т.е. вектор 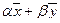 — решение однородной системы.
— решение однородной системы.
Остальные утверждения докажите аналогично самостоятельно.
Структура общего решения неоднородной системы
Вспомним одно из свойств решений линейной неоднородной системы:
Если  и
и 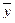 — два решения системы
— два решения системы  , то вектор
, то вектор 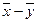 — решение приведенной однородной системы
— решение приведенной однородной системы 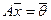 .
.
Поскольку выражение  задает все решения однородной системы, то для любых двух решений
задает все решения однородной системы, то для любых двух решений  и
и 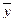 неоднородной системы справедливо
неоднородной системы справедливо
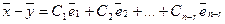 и, следовательно, выражение
и, следовательно, выражение 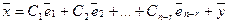 позволяет вычислить любое решение неоднородной системы.
позволяет вычислить любое решение неоднородной системы.
Таким образом доказана теорема о структуре общего решения линейной неоднородной системы.
Теорема о структуре общего решения неоднородной системы линейных алгебраических уравнений. Если ранг r матрицы неоднородной системы линейных уравнений меньше числа неизвестных n , то общее решение системы можно записать в виде
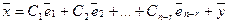
где 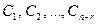 — произвольные константы, а
— произвольные константы, а 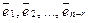 — фундаментальная система решений приведенной однородной системы,
— фундаментальная система решений приведенной однородной системы, 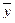 — некоторое известное (частное) решение неоднородной системы.
— некоторое известное (частное) решение неоднородной системы.
Формулы Крамера. Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных
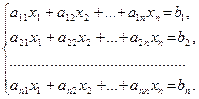
Обозначим: 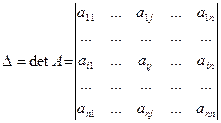 — определитель матрицы системы, и
— определитель матрицы системы, и 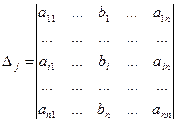 — определитель матрицы, полученной из матрицы системы заменой j-го столбца столбцом правых частей.
— определитель матрицы, полученной из матрицы системы заменой j-го столбца столбцом правых частей.
Если определитель матрицы системы отличен от нуля, 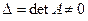 , то решение системы
, то решение системы
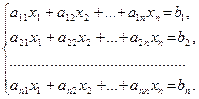
определяется равенствами: 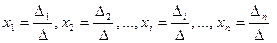 .
.
Докажем это утверждение. Пусть 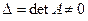 .
.
Обозначим  и покажем, что
и покажем, что 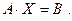 Вычислим
Вычислим
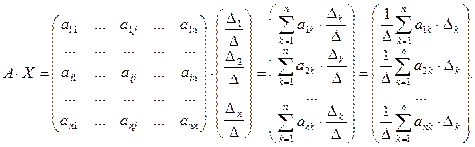
Вычислим определитель 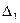 разложением по первому столбцу, определитель
разложением по первому столбцу, определитель 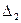 — по второму, …,
— по второму, …, 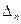 — по n-му:
— по n-му:
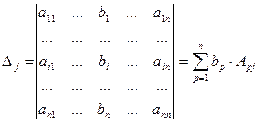 , поскольку определитель
, поскольку определитель 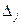 отличается от
отличается от 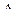 только j-м столбцом. Тогда
только j-м столбцом. Тогда
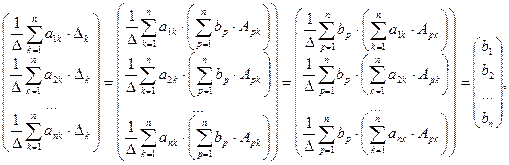
поскольку
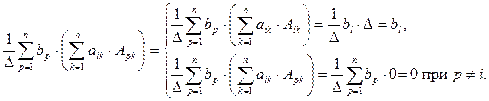
Т.е. 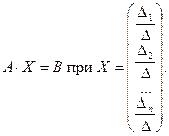 Формулы Крамера доказаны.
Формулы Крамера доказаны.
Замечание. Нетрудно, показать, что выражения 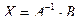 и
и 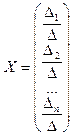 — две формы записи одного и того же равенства.
— две формы записи одного и того же равенства.
Действительно, 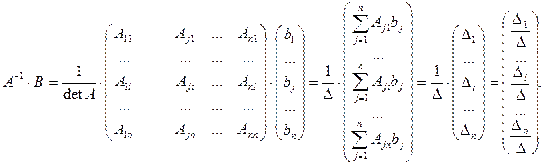
Лекция 6. Линейное пространство. Линейная зависимость системы векторов. Размерность, базис. Линейное подпространство. Примеры
Линейное пространство арифметических векторов Rn
Определение. Арифметическим вектором называется упорядоченная совокупность n чисел. Обозначается  , числа
, числа 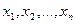 называются компонентами арифметического вектора.
называются компонентами арифметического вектора.
Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число:  для любых
для любых 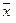 и
и 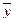 и любого числа
и любого числа 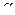
Определение. Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов Rn.
Вектор  называется нулевым вектором, а вектор
называется нулевым вектором, а вектор  — противоположным вектором для вектора
— противоположным вектором для вектора 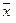 .
.
Для любых 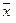 ,
, 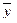 ,
, 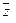 из Rn и любых чисел α , β справедливо:
из Rn и любых чисел α , β справедливо:
1. 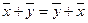 , сложение коммутативно;
, сложение коммутативно;
2. 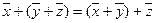 , сложение ассоциативно;
, сложение ассоциативно;
3. 
4. 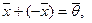
5.  , умножение на число дистрибутивно относительно сложения элементов;
, умножение на число дистрибутивно относительно сложения элементов;
6. 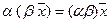 , умножение на число ассоциативно;
, умножение на число ассоциативно;
7.  , умножение вектора на число дистрибутивно относительно сложения чисел.
, умножение вектора на число дистрибутивно относительно сложения чисел.
8. 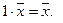
Примерами пространства арифметических векторов являются пространства геометрических векторов на плоскости, записанных в координатной форме.
Линейная зависимость и линейная независимость в Rn
Определение. Линейной комбинацией векторов 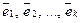 называется выражение
называется выражение 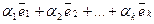 , где коэффициенты линейной комбинации
, где коэффициенты линейной комбинации 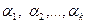 — некоторые числа.
— некоторые числа.
Определение. Говорят, что вектор 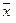 пространства Rn линейно выражается через векторы
пространства Rn линейно выражается через векторы 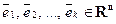 , если его можно представить в виде линейной комбинации этих элементов
, если его можно представить в виде линейной комбинации этих элементов 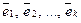 , т.е. представить в виде
, т.е. представить в виде 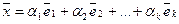 .
.
Определение. Система 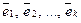 векторов из Rn называется линейно независимой если из
векторов из Rn называется линейно независимой если из 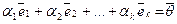 следует равенство нулю всех коэффициентов
следует равенство нулю всех коэффициентов 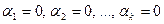 ,
, 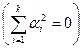 .
.
Иными словами, линейная комбинация векторов равна нулю тогда и только тогда, когда все коэффициенты линейной комбинации равны нулю. 
Определение. Система векторов, которая не является линейно зависимой, называется линейно независимой.
Иными словами, существуют такие коэффициенты линейной комбинации 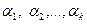 , не все равные нулю
, не все равные нулю  , что
, что 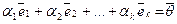 .
.
Или: линейная комбинация векторов может обратиться в нуль, хотя не все коэффициенты линейной комбинации равны нулю.
Пример. Исследуем на линейную зависимость векторы 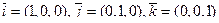 из R 3.
из R 3.
Составим линейную комбинацию векторов и приравняем ее нулю:
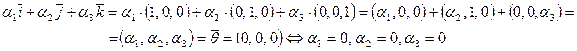
Т.е. линейная комбинация равна нулю тогда и только тогда, когда все ее коэффициенты нулевые — векторы  линейно независимы.
линейно независимы.
Пример. Исследуем на линейную зависимость систему векторов 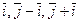 из R 3.
из R 3.
Составим линейную комбинацию векторов и приравняем ее нулю:
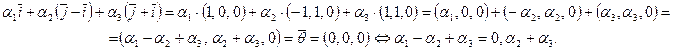 Пусть, например,
Пусть, например, 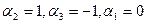 , тогда
, тогда 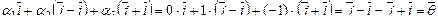 , т.е. существует нулевая линейная комбинация с отличными от нуля коэффициентами — векторы
, т.е. существует нулевая линейная комбинация с отличными от нуля коэффициентами — векторы 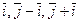 — линейно зависимы.
— линейно зависимы.
Свойства линейно зависимых и линейно независимых систем функций
1. Любая система векторов, содержащая нулевой вектор линейно зависима.
2. Любая система векторов, содержащая пару взаимно противоположных векторов — линейно зависима.
3. Любая система векторов, содержащая два равные вектора — линейно зависима.
4. Любая подсистема линейно независимой системы векторов — линейно независима.
5. Если некоторая подсистема системы векторов линейно зависима, то и вся система — линейно зависима.
Докажем первое из этих утверждений: любая система векторов, содержащая нулевой вектор линейно зависима. Рассмотрим произвольную систему векторов 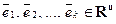 и добавим к ней нулевой вектор:
и добавим к ней нулевой вектор: 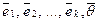 . Тогда :
. Тогда : 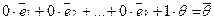 , т.е. равна нулю линейная комбинация с одним ненулевым коэффициентом — векторы линейно зависимы, ч.т.д.
, т.е. равна нулю линейная комбинация с одним ненулевым коэффициентом — векторы линейно зависимы, ч.т.д.
Остальные утверждения доказываются аналогично. Докажите сами.
Необходимое и достаточное условие линейной зависимости системы векторов в Rn
Справедливо следующее утверждение.
Теорема (Необходимое и достаточное условие линейной зависимости системы векторов). Система 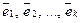 векторов из Rn линейно зависима тогда и только тогда, когда хотя бы один вектор системы векторов
векторов из Rn линейно зависима тогда и только тогда, когда хотя бы один вектор системы векторов 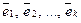 из Rn линейно выражается через остальные векторы системы.
из Rn линейно выражается через остальные векторы системы.
Доказательство теоремы. Необходимость. Дано: векторы 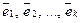 линейно зависимы. Докажем, что хотя бы один из них линейно выражается через остальные .
линейно зависимы. Докажем, что хотя бы один из них линейно выражается через остальные .
Векторы 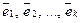 линейно зависимы. Это означает, что существуют такие коэффициенты линейной комбинации
линейно зависимы. Это означает, что существуют такие коэффициенты линейной комбинации 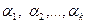 , не все равные нулю, что
, не все равные нулю, что 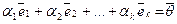 .
.
Не умаляя общности, предположим, что именно 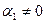 . Тогда из
. Тогда из 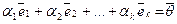 следует:
следует: 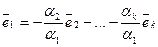 — вектор
— вектор 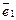 линейно выражается через
линейно выражается через 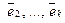 . Необходимость доказана.
. Необходимость доказана.
Достаточность. Дано: один из векторов системы 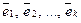 линейно выражается через остальные. Докажем, что векторы линейно зависимы.
линейно выражается через остальные. Докажем, что векторы линейно зависимы.
Действительно, не умаляя общности, положим, что вектор 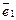 линейно выражается через
линейно выражается через 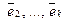 :
: 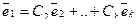 . Если все
. Если все  , то
, то  и векторы
и векторы  линейно зависимы (см. св-во 1). Если же среди
линейно зависимы (см. св-во 1). Если же среди  есть хоть одно отличное от нуля число, то
есть хоть одно отличное от нуля число, то 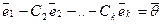 — имеем нулевую линейную комбинацию, не все коэффициенты которой равны нулю — система векторов
— имеем нулевую линейную комбинацию, не все коэффициенты которой равны нулю — система векторов 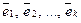 линейно зависима. Достаточность доказана. Теорема доказана.
линейно зависима. Достаточность доказана. Теорема доказана.
Базис в Rn. Координаты вектора в заданном базисе. Линейные операции в координатной форме
Определение. Система векторов из R n образует базис в R n если:
1. система векторов упорядочена;
2. система векторов линейно независима;
3. любой вектор из R n линейно выражается через векторы системы.
Иными словами, линейно независимая упорядоченная система векторов 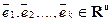
Образует базис в R n если любой вектор 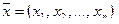
 из Rn может быть представлен в виде
из Rn может быть представлен в виде  .
.
Определение. Выражение  называется разложением вектора в базисе
называется разложением вектора в базисе 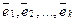 , а числа
, а числа 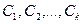 называются координатами вектора
называются координатами вектора 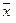 в базисе
в базисе 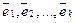 .
.
Пример. Нетрудно доказать, что система арифметических векторов
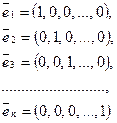
линейно независима (см. пример с  ) и что для любого
) и что для любого  из Rn система векторов
из Rn система векторов 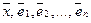 линейно зависима, поскольку любой вектор
линейно зависима, поскольку любой вектор 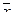 линейно выражается через
линейно выражается через 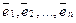 :
:  . Т.е. в Rn существует базис, состоящий из n векторов. Базис
. Т.е. в Rn существует базис, состоящий из n векторов. Базис  называется естественным базисом в Rn, и компоненты вектора
называется естественным базисом в Rn, и компоненты вектора 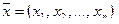 — его координаты в естественном базисе.
— его координаты в естественном базисе.
Справедливо следующее утверждение.
Теорема (о единственности разложения вектора в базисе). Для любого вектора 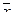 из Rn разложение
из Rn разложение  вектора в базисе
вектора в базисе 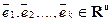 единственно.
единственно.
Доказательство теоремы. «От противного». Пусть не так. Т.е. векторы 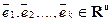 образуют базис в Rn , помимо разложения
образуют базис в Rn , помимо разложения  , существует разложение
, существует разложение 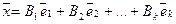 и не все коэффициенты Ci , Bi совпадают.
и не все коэффициенты Ci , Bi совпадают.
Тогда 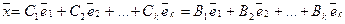 , и, следовательно,
, и, следовательно, 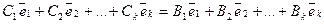 , откуда
, откуда 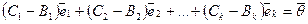 .
.
Но векторы 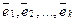 образуют базис, — они линейно независимы, и, следовательно,
образуют базис, — они линейно независимы, и, следовательно, 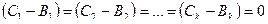 , т.е.
, т.е.  — все коэффициенты разложений соответственно равны — разложения совпадают. Теорема доказана.
— все коэффициенты разложений соответственно равны — разложения совпадают. Теорема доказана.
Следствие. Координаты вектора в заданном базисе определяются единственным образом.
Теорема. В пространстве Rn существует базис из n векторов.
Действительно, этот базис — естественный базис 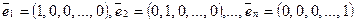
Линейные операции в координатной форме
Пусть векторы  образуют базис в Rn. Тогда для любых двух векторов
образуют базис в Rn. Тогда для любых двух векторов 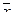 и
и
 из Rn однозначно определены разложения
из Rn однозначно определены разложения  ,
, 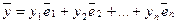 . Тогда из свойств арифметических операций в Rn следует:
. Тогда из свойств арифметических операций в Rn следует:
 и
и
для любого числа 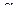 :
: 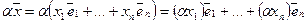 .
.
Иными словами, координаты суммы векторов в заданном базисе равны сумме соответствующих координат слагаемых, а координаты произведения вектора на число — произведению соответствующих координат вектора на число.
Линейные подпространства в Rn, размерность подпространства, базис в подпространстве
Определение. Множество L векторов из Rn , такое, что для любых 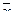 и
и 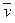 из L и любого числа α справедливо
из L и любого числа α справедливо 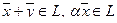 , называется линейным подпространством в Rn.
, называется линейным подпространством в Rn.
Пример. Множество L арифметических векторов из Rn, у которых последние компоненты — нулевые, образует линейное подпространство в Rn:
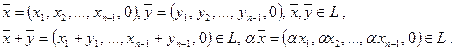
Нетрудно доказать, что для любого линейного подпространства справедливо:
- если вектор
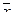 принадлежит линейному подпространству L, то и вектор
принадлежит линейному подпространству L, то и вектор 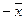 принадлежит линейному подпространству L;
принадлежит линейному подпространству L; - любое линейное подпространство содержит нулевой элемент.
Действительно, пусть 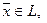 но тогда и
но тогда и 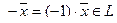 , и, следовательно,
, и, следовательно,  .
.
Утверждение. Пространство Rn само является линейным подпространством в Rn.
Это утверждение очевидно, поскольку сумма любых двух векторов из Rn и произведение любого вектора из Rn на любое число принадлежат Rn.
Определение. Число k называется размерностью линейного подпространства L , если в L существует система из k линейно независимых векторов, а любые k +1 вектора — линейно зависимы. Обозначаем dimL = k .
Нетрудно доказать следующее утверждение.
Теорема. В k -мерном линейном подпространстве существует базис их k векторов.
Доказательство теоремы. Действительно, если dimL = k, то существует система из k линейно независимых векторов 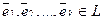 , а любая система из k+1 вектора
, а любая система из k+1 вектора  — линейно зависима, но тогда любой вектор
— линейно зависима, но тогда любой вектор 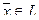 линейно выражается через векторы :
линейно выражается через векторы :  , т.е.
, т.е. 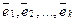 — базис в L.
— базис в L.
Справедливы также следующие утверждения (оставим их без доказательства).
Теорема. Любая упорядоченная система из k линейно независимых векторов k -мерного линейного подпространства является базисом в этом подпространстве.
Теорема. Размерность линейного подпространства равна числу векторов в базисе этого подпространства.
Отсюда следует: dim ( Rn ) = n.
Действительно, в пространстве Rn есть базис из n векторов — естественный базис в Rn.
Пример. Размерность линейного подпространства L арифметических векторов из Rn, у которых последние компоненты — нулевые, равна n – 1.
Действительно, векторы 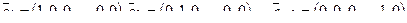 — очевидно, принадлежат L и линейно независимы. Покажем, что они образуют базис в L. Для произвольного вектора
— очевидно, принадлежат L и линейно независимы. Покажем, что они образуют базис в L. Для произвольного вектора 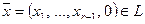 имеет место разложение справедливо:
имеет место разложение справедливо:  , т.е. векторы
, т.е. векторы 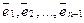 образуют базис в L. В этом базисе n-1 вектор, следовательно, dimL = n –1.
образуют базис в L. В этом базисе n-1 вектор, следовательно, dimL = n –1.
Тогда можно использовать другое определение базиса.
Определение. Любая упорядоченная линейно независимая система из k векторов k -мерного линейного подпространства L образует базис этого линейного подпространства L .
Это означает, что если dimL = k и арифметические векторы 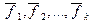 из L линейно независимы, то для любого
из L линейно независимы, то для любого 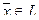 существует единственный набор чисел
существует единственный набор чисел 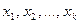 таких, что
таких, что 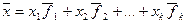 .
.
Метрические соотношения в Rn
Определение. Если каждой паре векторов 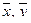 из пространства Rn поставлено в соответствие действительное число
из пространства Rn поставлено в соответствие действительное число 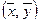 , так, что для любых
, так, что для любых 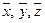 из Rn и любого действительного числа
из Rn и любого действительного числа 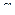 справедливы следующие равенства:
справедливы следующие равенства:
1. 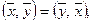
2. 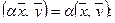
3. 
4. 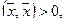 при
при 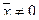 ,
, 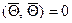 ,
, 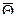 — нулевой вектор,
— нулевой вектор,
то говорят, что в пространстве Rn определено скалярное произведение 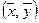 .
.
Пример. Легко проверить, что изученное в разделе «аналитическая геометрия» скалярное произведение известное из школьного курса скалярное произведение в трехмерном пространстве геометрических векторов (в R 3) является скалярным произведением в определенном выше смысле.
Пример. Рассмотрим пространство арифметических векторов R 2 ={X=(x1, x2)}. Определим скалярное произведение следующим образом:
(X, Y) = 2x1y1 + 3x2y2.
Легко убедиться, что для определенного таким образом скалярного произведения справедливы аксиомы 1. — 4.:
(X, Y) = 2x1y1 + 3x2y2 = 2y1x1 + 3y2x2 = (Y, X),
(aX, Y) = 2(ax1)y1 + 3(ax2)y2 = a(2y1x1 + 3y2x2) = a (X, Y),
(X+Y, Z) = 2(x1+y1)z1 + 3(x2+y2)z2 = (2x1z1 + 3x2z2) + (2y1z1 + 3y2z2) = (X, Z) + (Y, Z),
(X , X) = 2x1x1 + 3x2x2 = 2x12 + 3x22 >0 если 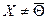 , если же X = (0, 0), то (X , X) = 0.
, если же X = (0, 0), то (X , X) = 0.
Вернемся к пространству арифметических векторов Rn = { 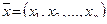 }
}
Определим в Rn естественное скалярное произведение: каждой паре векторов 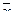 и
и 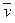 из этого пространства поставим в соответствие действительное число
из этого пространства поставим в соответствие действительное число 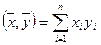 . Нетрудно доказать, что для любых векторов
. Нетрудно доказать, что для любых векторов 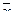 ,
, 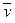 и
и 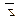 и любого действительного числа
и любого действительного числа  для
для 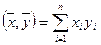 справедливо:
справедливо:
1. 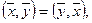
2. 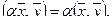
3. 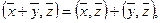
4. 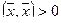 при
при 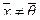 , и
, и 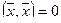 тогда и только тогда, когда
тогда и только тогда, когда 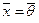 ,
, 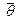 — нулевой вектор.
— нулевой вектор.
Пространство арифметических векторов Rn с определенным в нем естественным скалярным произведением называют евклидовым пространством арифметических векторов и иногда обозначают En.
Свойства скалярного произведения. Неравенство Коши-Буняковского
Теорема (неравенство Коши-Буняковского). Для любых векторов 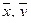 из пространства Rn справедливо следующее неравенство
из пространства Rn справедливо следующее неравенство 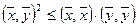 .
.
Доказательство теоремы. Возьмем произвольное число 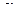 и рассмотрим
и рассмотрим 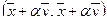 . По последнему свойству скалярного произведения для любых векторов
. По последнему свойству скалярного произведения для любых векторов 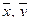 и любого числа
и любого числа 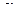 справедливо:
справедливо: 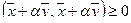 . С другой стороны,
. С другой стороны, 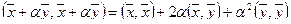 , т.е.
, т.е.  . Выражение в левой части неравенства — квадратный трехчлен относительно
. Выражение в левой части неравенства — квадратный трехчлен относительно 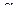 . Он неотрицателен тогда и только тогда, когда дискриминант
. Он неотрицателен тогда и только тогда, когда дискриминант  . Из последнего неравенства немедленно следует неравенство Коши-Буняковского:
. Из последнего неравенства немедленно следует неравенство Коши-Буняковского: 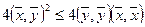 ,
,  . Теорема доказана.
. Теорема доказана.
Метрические соотношения в Rn
Определение. Число 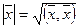 называется длиной вектора
называется длиной вектора 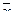 ; число
; число  — расстоянием между векторами
— расстоянием между векторами 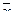 и
и 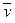 ; угол
; угол  , косинус которого
, косинус которого 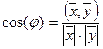 — углом между векторами
— углом между векторами 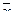 и
и 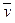 .
.
Если в Rn скалярное произведение определено формулой 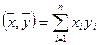 , то для любых
, то для любых 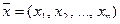 ,
, 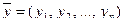 из Rn справедливо:
из Rn справедливо:
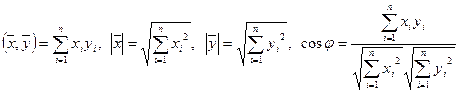
Ортогональность, ортогональные системы, ортонормированные базисы
Определение. Векторы  и
и 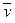 из пространства Rn называются ортогональными, если
из пространства Rn называются ортогональными, если 
Определение. Система 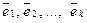 векторов из пространства Rn называется ортогональной, если векторы системы попарно ортогональны.
векторов из пространства Rn называется ортогональной, если векторы системы попарно ортогональны.
Теорема (о линейной независимости ортогональных систем). Ортогональная система векторов линейно независима.
Доказательство теоремы.
Предположим противное: векторы 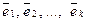 попарно ортогональны, но они линейно зависимы. Тогда один из векторов линейно выражается через остальные. Например, пусть это первый вектор:
попарно ортогональны, но они линейно зависимы. Тогда один из векторов линейно выражается через остальные. Например, пусть это первый вектор:  ,
,  (ясно, что речь идет о ненулевых векторах). Тогда
(ясно, что речь идет о ненулевых векторах). Тогда 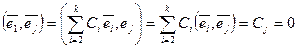 , для всех j = 2, 3, …, k, т.е.
, для всех j = 2, 3, …, k, т.е. 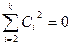 . Полученное противоречие доказывает теорему.
. Полученное противоречие доказывает теорему.
Определение. Система  векторов из пространства Rn называется ортонормированной, если векторы системы попарно ортогональны и имеют единичную длину.
векторов из пространства Rn называется ортонормированной, если векторы системы попарно ортогональны и имеют единичную длину.
Определение. Базис пространства Rn называется ортонормированным базисом, если образующие его векторы попарно ортогональны и имеют единичную длину.
В пространстве Rn в естественном скалярном произведении 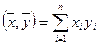 естественный базис — ортонормированный базис.
естественный базис — ортонормированный базис.
Подпространство строк и подпространство столбцов прямоугольной матрицы
Рассмотрим прямоугольную матрицу Am , n, у которой m строк и n столбцов:
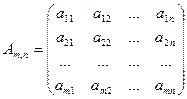 .
.
Её строки — 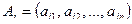 —являются векторами из Rn,
—являются векторами из Rn,
А столбцы — 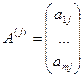 — являются векторами из Rm.
— являются векторами из Rm.
Понятно, что множество строк матрицы Am , n , к которому добавили все строки, которые могут быть получены при элементарных преобразованиях матрицы (исключая транспонирование) — линейное подпространство в Rn.
А аналогично образованное множество столбцов — линейное подпространство в Rm.
Это означает, что мы можем говорить о линейной зависимости и о линейной независимости строк и столбцов матрицы, о размерности подпространства строк и подпространства столбцов матрицы, о базисах в соответствующих подпространствах.
Примеры.
1. Нулевой оператор 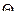 :
: 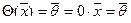 , т.е.
, т.е. 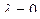 — собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn.
— собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn.
2. Тождественный (единичный) оператор I: 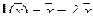 — т.е.
— т.е. 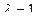 собственное значение тождественного оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn.
собственное значение тождественного оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn.
3. Оператор P 2 — оператор проектирования пространства R 3 на подпространство R 2 параллельно вектору 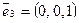 :
:  ,
, 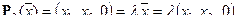 , т.е.
, т.е. 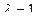 — собственное значение оператора, проектирования, а соответствующие собственные векторы — все ненулевые векторы R3, третья координата которых равна нулю:
— собственное значение оператора, проектирования, а соответствующие собственные векторы — все ненулевые векторы R3, третья координата которых равна нулю: 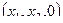 .
.
Пусть A— матрица оператора в некотором базисе в Rn.
Собственные значения оператора и соответствующие им собственные векторы связаны соотношением 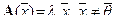 или, что то же самое,
или, что то же самое,  :
:
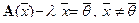 ,
, 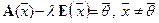 . Здесь
. Здесь 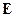 — единичный оператор.
— единичный оператор.
По теореме о связи координат образа и прообраза имеем: 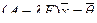 , где E — единичная матрица, а
, где E — единичная матрица, а 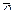 — нулевой вектор Rn .
— нулевой вектор Rn .
Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы 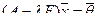 . Ненулевое решение однородной системы (система нетривиально совместна), существует тогда и только тогда, когда определитель матрицы системы равен нулю:
. Ненулевое решение однородной системы (система нетривиально совместна), существует тогда и только тогда, когда определитель матрицы системы равен нулю: 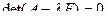 . Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения
. Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения 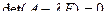 , а собственные векторы — как решения соответствующих однородных систем.
, а собственные векторы — как решения соответствующих однородных систем.
Легко видеть, что определитель 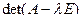 — многочлен n-й степени относительно
— многочлен n-й степени относительно 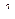 .
.
Определение. Уравнение 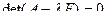 называется характеристическим уравнением оператора, а многочлен
называется характеристическим уравнением оператора, а многочлен  — характеристическим многочленом оператора.
— характеристическим многочленом оператора.
Примеры.
1. Нулевой оператор 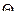 :
:  , матрица нулевого оператора — нулевая матрица соответствующего порядка, т.е.
, матрица нулевого оператора — нулевая матрица соответствующего порядка, т.е.  т.е.
т.е. 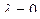 — единственное собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn.
— единственное собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn.
2. Тождественный (единичный) оператор I: 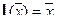 матрица тождественного оператора — единичная матрица соответствующего порядка, т.е.
матрица тождественного оператора — единичная матрица соответствующего порядка, т.е. 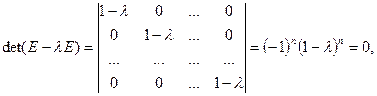 т.е.
т.е. 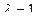 — единственное собственное значение тождественного оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn.
— единственное собственное значение тождественного оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rn.
3. Оператор P 2 — оператор проектирования пространства R 3 на подпространство R 2 параллельно вектору 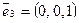 :
:  , тогда матрица тождественного оператора — единичная матрица соответствующего порядка, т.е.
, тогда матрица тождественного оператора — единичная матрица соответствующего порядка, т.е. 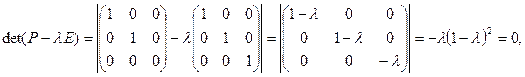 т.е.
т.е. 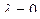 и
и 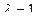 — собственные значения оператора.
— собственные значения оператора.
Найдем соответствующие собственные векторы.
Пусть 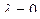 , тогда соответствующие собственные векторы — ненулевые решения системы
, тогда соответствующие собственные векторы — ненулевые решения системы  т.е.
т.е.
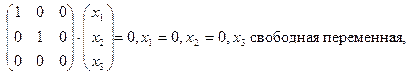 т.е. вектор
т.е. вектор
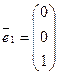 — собственный вектор оператора, отвечающий собственному значению
— собственный вектор оператора, отвечающий собственному значению 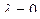 и, следовательно, все векторы вида
и, следовательно, все векторы вида 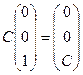 — собственные векторы оператора, отвечающие собственному значению
— собственные векторы оператора, отвечающие собственному значению 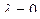 .
.
Теперь положим 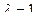 , тогда соответствующие собственные векторы — ненулевые решения системы
, тогда соответствующие собственные векторы — ненулевые решения системы 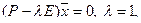 т.е.
т.е.
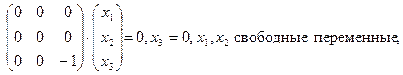 т.е. векторы
т.е. векторы
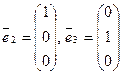 — линейно независимые векторы, которые являются собственными векторами оператора, отвечающими собственному значению
— линейно независимые векторы, которые являются собственными векторами оператора, отвечающими собственному значению 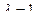 и, следовательно, все векторы вида
и, следовательно, все векторы вида 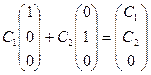 — собственные векторы оператора, отвечающие собственному значению
— собственные векторы оператора, отвечающие собственному значению 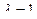 .
.
4. . Оператор Uj поворота пространства R 2 на угол φ относительно начала координат против часовой стрелки:
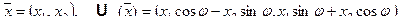 .
.
Матрица оператора 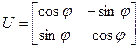 , тогда
, тогда 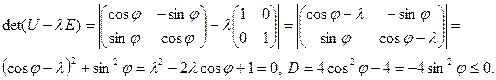
Характеристическое уравнение имеет единственный корень  при
при 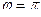 и
и 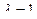 при
при 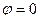 ,
,  . Если
. Если 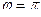 ,
,  , и
, и 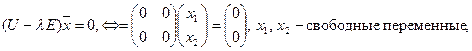 т.е. соответствующие собственные векторы — все ненулевые векторы пространства R2.
т.е. соответствующие собственные векторы — все ненулевые векторы пространства R2.
При 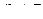 — оператор поворота не имеет собственных векторов.
— оператор поворота не имеет собственных векторов.
И, наконец, при 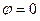 и
и  ,
, 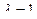 , оператор поворота совпадает с тождественным оператором, собственные значения и собственные векторы которого вычислены выше.
, оператор поворота совпадает с тождественным оператором, собственные значения и собственные векторы которого вычислены выше.
Однако, все приведенные выше рассуждения относились к матрице оператора, записанной в некотором определенном базисе в пространстве Rn. А поскольку в пространстве Rn существует много различных базисов, то может возникнуть впечатление, что собственные значения зависят от выбранного базиса. Докажем, что это не так.
Пусть 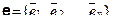 и
и 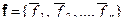 — два базиса в Rn, а
— два базиса в Rn, а 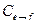 — матрица перехода от базиса
— матрица перехода от базиса 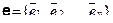 к базису
к базису 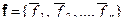 , т.е.
, т.е.  . Тогда
. Тогда
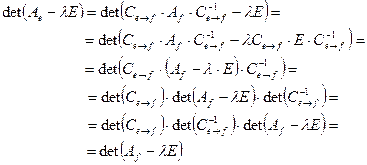
т.е. характеристическое уравнение инвариантно, не зависит от базиса и его корни — собственные значения оператора — не зависят от базиса.
Свойства собственных векторов
Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:
1) характеристический многочлен оператора, действующего в Rn является многочленом n-й степени относительно 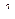 ;
;
2) линейный оператор, действующий в Rn, имеет не более n различных собственных значений;
3) собственные векторы оператора определяются с точностью до постоянного сомножителя; поэтому принять вычислять собственные векторы единичной длины — орты собственных векторов;
докажем, что если  — собственный вектор линейного оператора A, отвечающий собственному значению
— собственный вектор линейного оператора A, отвечающий собственному значению 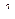 , то для любого отличного от нуля числа
, то для любого отличного от нуля числа  вектор
вектор  (
( 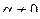 )— собственный вектор оператора A, отвечающий собственному значению
)— собственный вектор оператора A, отвечающий собственному значению 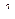 :
: 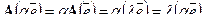 ;
;
4) корни характеристического многочлена не зависят от базиса;
5) собственные векторы, отвечающие различным собственным значениям, линейно независимы.
Докажем линейную независимость собственных векторов, отвечающих различным собственным значениям.
Пусть  — собственный вектор линейного оператора A, отвечающий собственному значению
— собственный вектор линейного оператора A, отвечающий собственному значению 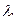 , а
, а 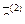 — собственный вектор линейного оператора A, отвечающий собственному значению
— собственный вектор линейного оператора A, отвечающий собственному значению 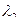 ,
, 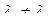 :
: 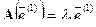 и
и 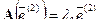 .
.
Предположим, что векторы  и
и 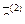 линейно зависимы. Это означает, что один из них линейно выражается через другой: существует такое число
линейно зависимы. Это означает, что один из них линейно выражается через другой: существует такое число 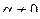 , что
, что 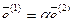 . Тогда:
. Тогда:
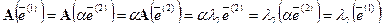 .
.
Собственный базис линейного оператора. Матрица линейного оператора в собственном базисе
Если линейный оператор, действующий в Rn, имеет n различных собственных значений, то собственные векторы оператора образуют базис в Rn.
Действительно, ведь мы доказали, что они линейно независимы.
Определение. Базис, составленный из собственных векторов линейного оператора называют собственным базисом оператора.
Если 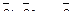 — собственный базис оператора A, то, поскольку
— собственный базис оператора A, то, поскольку  то матрица оператора в этом базисе — диагональная матрица с собственными значениями на диагонали.
то матрица оператора в этом базисе — диагональная матрица с собственными значениями на диагонали.
Окружность
Начнем с определения окружности, известного из школьного курса математики.
Определение 12.2 Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности.
Получим уравнение окружности, если известны ее центр и радиус.
Теорема 12.1 Окружность радиуса  с центром в точке
с центром в точке 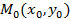 имеет уравнение
имеет уравнение
|
| (8.2) |
Доказательство. Пусть 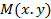 -- текущая точка окружности. По определению окружности расстояние
-- текущая точка окружности. По определению окружности расстояние 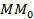 равно
равно  (рис. 8.1)
(рис. 8.1)

Рис.8.1.Окружность
По формуле для плоскости получаем, что точки окружности и только они удовлетворяют уравнению
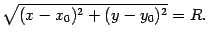
Обе части уравнения неотрицательны. Поэтому после возведения их в квадрат получим эквивалентное уравнение (8.2).
Если в уравнении (8.2) раскрыть скобки и привести подобные члены, то вид его изменится. Однако любое уравнение окружности с помощью тождественных преобразований можно привести к виду (8.2). Для этого достаточно выделить полные квадраты по переменным 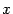 и
и 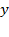 .
.
Эллипс
Определение 8.3 Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек той же плоскости, назывемых фокусами эллипса, есть величина постоянная.
Для эллипса можно дать еще несколько эквивалентных определений. Желающие могут познакомиться с ними в более серьезных учебниках по аналитической геометрии. Здесь же отметим только то, что эллипс -- это кривая, получающаяся как проекция на плоскость 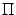 окружности, лежащей в плоскости, которая образует острый угол с плоскостью
окружности, лежащей в плоскости, которая образует острый угол с плоскостью 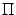 .
.
В отличие от окружности, записать в "удобном" виде уравнение эллипса в произвольной системе координат не удается. Поэтому для фиксированного эллипса приходится подбирать систему координат так, чтобы его уравнение было достаточно простым.
Пусть 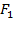 и
и 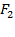 -- фокусы эллипса. Начало
-- фокусы эллипса. Начало 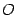 системы координат расположим на середине отрезка
системы координат расположим на середине отрезка  . Ось
. Ось 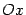 направим вдоль этого отрезка, ось Oy-- перпендикулярно к этому отрезку (рис. 12.3).
направим вдоль этого отрезка, ось Oy-- перпендикулярно к этому отрезку (рис. 12.3).
Теорема 12.2 Пусть сумма расстояний от точки эллипса до фокусов равна  , а расстояние между фокусами --
, а расстояние между фокусами -- 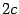 . Тогда в выбранной системе координат эллипс имеет уравнение
. Тогда в выбранной системе координат эллипс имеет уравнение
|
| (12.4) |
где
|
| (12.5) |
Доказательство. Пусть 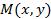 -- текущая точка эллипса. По определению эллипса
-- текущая точка эллипса. По определению эллипса 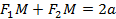 . Из треугольника
. Из треугольника  (рис. 12.3) видно, что
(рис. 12.3) видно, что  , то есть
, то есть  ,
,  , и поэтому число
, и поэтому число  существует.
существует.
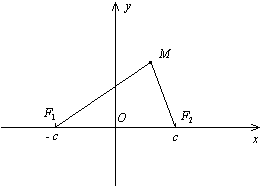
Рис.12.3.
Фокусами в выбранной системе координат являются точки 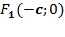 ,
,  .
.
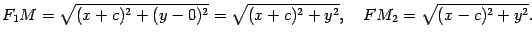
Тогда по определению эллипса
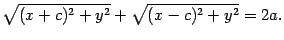
Пренесем один из корней вправо и обе части возведем в квадрат:
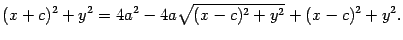
После того, как раскроем скобки и приведем подобные члены, приходим к выражению
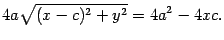
Разделим обе части этого уравнения на 4 и возведем в квадрат
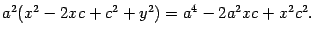
Раскроем скобку и приведем подобные члены

Учитывая, что 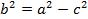 , имеем равенство
, имеем равенство
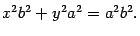
Наконец, разделив обе части на  , получим уравнение (12.4).
, получим уравнение (12.4).
Уравнение (12.4) называется каноническим уравнением эллипса.
Прежде, чем нарисовать эллипс, выясним некоторые его свойства.
Предложение 12.1 Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центром симметрии. Если эллипс задан каноническим уравнением ( 12.4 ), то его осями симметрии служат оси 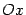 и
и 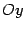 , начало координат -- центр симметрии.
, начало координат -- центр симметрии.
Доказательство. Можно было бы провести доказательство на основе определения эллипса (предлагаем читателю попробовать сделать это), но для усиления аналитического аспекта мы проведем доказательство на основе уравнения (12.4).
Пусть эллипс задан уравнением (12.4) и 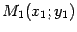 -- какая-то точка эллипса. Тогда
-- какая-то точка эллипса. Тогда
|
| (12.6) |
Точка 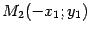 является точкой, симметричной точке
является точкой, симметричной точке  относительно оси
относительно оси  (рис. 12.4).
(рис. 12.4).
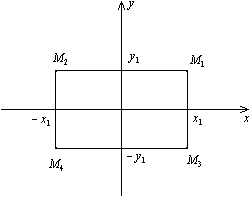
Рис.12.4.Симметрия точек
Вычисляем значение левой части уравнения (12.4) в точке 
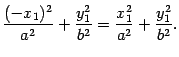
В силу равенства (12.6) получаем
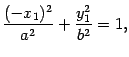
следовательно, точка  лежит на эллипсе. Точка
лежит на эллипсе. Точка  является точкой симметричной
является точкой симметричной  точке относительно оси
точке относительно оси  (рис. 12.4). Для нее аналогичным путем убеждаемся, что
(рис. 12.4). Для нее аналогичным путем убеждаемся, что

то есть  является точкой эллипса. Наконец точка
является точкой эллипса. Наконец точка 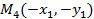 является симметричной точке
является симметричной точке  относительно начала координат (рис. 12.4). Повторяя предыдущие рассуждения, получим, что и эта точка тоже лежит на эллипсе. Итак, утверждение предложения доказано, если эллипс имеет уравнение (12.4). А так как по теореме 12.2 любой эллипс в некоторой системе координат имеет такое уравнение, то предложение полностью доказано.
относительно начала координат (рис. 12.4). Повторяя предыдущие рассуждения, получим, что и эта точка тоже лежит на эллипсе. Итак, утверждение предложения доказано, если эллипс имеет уравнение (12.4). А так как по теореме 12.2 любой эллипс в некоторой системе координат имеет такое уравнение, то предложение полностью доказано.
Гипербола
Из школьного курса математики известно, что кривая, задаваемая уравнением 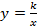 , где
, где  -- число, называется гиперболой. Однако это -- частный случай гиперболы (равносторонняя гипербола).
-- число, называется гиперболой. Однако это -- частный случай гиперболы (равносторонняя гипербола).
Определение 12.5 Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек той же плоскости, называемых фокусами гиперболы, есть величина постоянная.
Так же, как и в случае эллипса, для получения уравнения гиперболы выберем подходящую систему координат. Начало координат расположим на середине отрезка между фокусами, ось 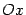 направим вдоль этого отрезка, а ось ординат -- перпендикулярно к нему.
направим вдоль этого отрезка, а ось ординат -- перпендикулярно к нему.
Теорема 12.3 Пусть расстояние между фокусами  и
и 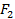 гиперболы равно
гиперболы равно 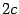 , а абсолютная величина разности расстояний от точки гиперболы до фокусов равна
, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна  . Тогда гипербола в выбранной выше системе координат имеет уравнение
. Тогда гипербола в выбранной выше системе координат имеет уравнение
|
| (12.8) |
где
|
| (12.9) |
Доказательство. Пусть 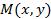 -- текущая точка гиперболы (рис. 12.9).
-- текущая точка гиперболы (рис. 12.9).
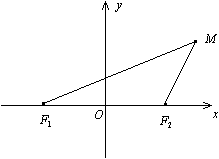
Рис.12.9.
Так как разность двух сторон треугольника меньше третьей стороны, то 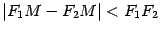 , то есть
, то есть 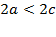 ,
, 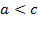 . В силу последнего неравенства вещественное число
. В силу последнего неравенства вещественное число 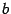 , определяемое формулой (12.9), существует.
, определяемое формулой (12.9), существует.
По условию, фокусы -- 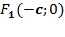 ,
,  . По формуле (10.4) для случая плоскости получаем
. По формуле (10.4) для случая плоскости получаем
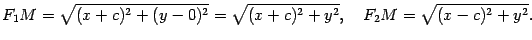
По определению гиперболы
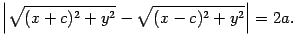
Это уравнение запишем в виде
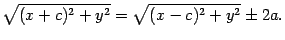
Обе части возведем в квадрат:
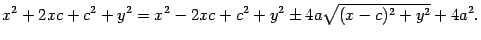
После приведения подобных членов и деления на 4, приходим к равенству
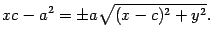
Опять обе части возведем в квадрат:
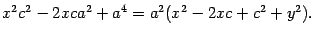
Раскрывая скобку и приводя подобные члены, получим
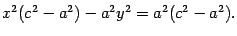
С учетом формулы (12.9) уравнение принимает вид
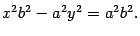
Разделим обе части уравнения на  и получим уравнение (12.8)
и получим уравнение (12.8)
Уравнение (12.8) называется каноническим уравнением гиперболы.
Предложение 12.3 Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением, то ее осями симметрии служат координатные оси  и Oy, а начало координат -- центр симметрии гиперболы.
и Oy, а начало координат -- центр симметрии гиперболы.
Доказательство. Проводится аналогично доказательству предложения 12.1.
Проведем построение гиперболы, заданной уравнением (12.8). Заметим, что из-за симметрии достаточно построить кривую только в первом координатном угле. Выразим из канонического уравнения y как функцию  , при условии, что
, при условии, что 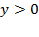 ,
,

и построим график этой функции.
Область определения -- интервал 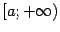 ,
, 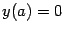 , функция монотонно растет. Производная
, функция монотонно растет. Производная
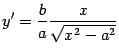
существует во всей области определения, кроме точки 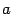 . Следовательно, график -- гладкая кривая (без углов). Вторая производная
. Следовательно, график -- гладкая кривая (без углов). Вторая производная
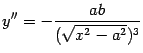
во всех точках интервала 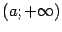 отрицательна, следовательно, график -- выпуклый вверх.
отрицательна, следовательно, график -- выпуклый вверх.
Проверим график на наличие асимптоты при 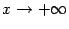 . Пусть асимптота имеет уравнение
. Пусть асимптота имеет уравнение 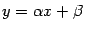 . Тогда по правилам математического анализа
. Тогда по правилам математического анализа
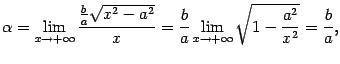
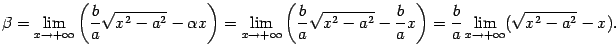
Выражение под знаком предела домножим и разделим на 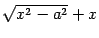 . Получим
. Получим
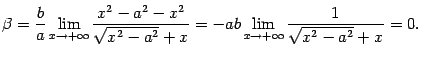
Итак, график функции имеет асимптоту 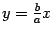 . Из симметрии гиперболы следует, что
. Из симметрии гиперболы следует, что 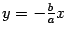 -- тоже асимптота. Остается неясным характер кривой в окрестности точки
-- тоже асимптота. Остается неясным характер кривой в окрестности точки 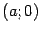 , а именно, образует ли график
, а именно, образует ли график 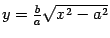 и симметричная ему относительно оси
и симметричная ему относительно оси 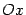 часть гиперболы в этой точке угол или гипербола в этой точке -- гладкая кривая (есть касательная). Для решения этого вопроса выразим из уравнения (12.8)
часть гиперболы в этой точке угол или гипербола в этой точке -- гладкая кривая (есть касательная). Для решения этого вопроса выразим из уравнения (12.8) 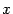 через
через 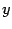 :
:

Очевидно, что данная функция имеет производную в точке 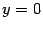 ,
, 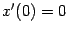 , и в точке
, и в точке 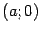 у гиперболы есть вертикальная касательная. По полученным данным рисуем график функции
у гиперболы есть вертикальная касательная. По полученным данным рисуем график функции 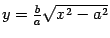 (рис. 12.10).
(рис. 12.10).
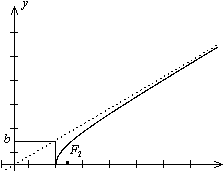
Рис.12.10.График функции 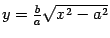
Окончательно, используя симметрию гиперболы, получаем кривую рисунка 12.11.
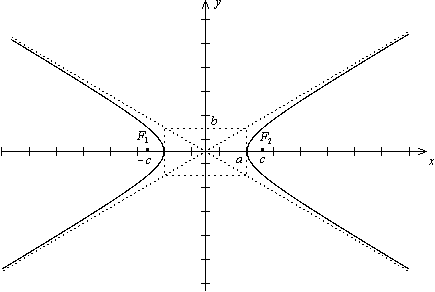
Рис.12.11.Гипербола
Определение 12.6 Точки пересечения гиперболы, заданной каноническим уравнением (12.8), с осью  называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками
называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками 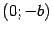 и
и 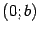 называется мнимой осью. Числа
называется мнимой осью. Числа 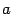 и
и 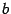 называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром. Величина
называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром. Величина 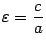 называется эксцентриситетом гиперболы.
называется эксцентриситетом гиперболы.
Замечание 12.3 Из равенства (12.9) следует, что 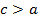 , то есть у гиперболы
, то есть у гиперболы 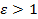 . Эксцентриситет
. Эксцентриситет 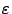 характеризует угол между асимптотами, чем ближе
характеризует угол между асимптотами, чем ближе 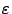 к 1, тем меньше этот угол.
к 1, тем меньше этот угол.
Замечание 12.4 В отличие от эллипса в каноническом уравнении гиперболы соотношение между величинами 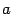 и
и 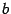 может быть произвольным. В частности, при
может быть произвольным. В частности, при 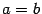 мы получим равностороннюю гиперболу, известную из школьного курса математики. Ее уравнение имеет знакомый вид
мы получим равностороннюю гиперболу, известную из школьного курса математики. Ее уравнение имеет знакомый вид 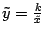 , если взять
, если взять 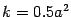 , а оси
, а оси  и
и  направить по биссектрисам четвертого и первого координатных углов (рис. 12.12).
направить по биссектрисам четвертого и первого координатных углов (рис. 12.12).

Рис.12.12.Равносторонняя гипербола 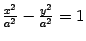
Для отражения на рисунке качественных характеристик гиперболы достаточно определить ее вершины, нарисовать асимптоты и нарисовать гладкую кривую, проходящую через вершины, приближающуюся к асимптотам и похожую на кривую рисунка 12.10.
Парабола
В школьном курсе математики достаточно подробно изучалась парабола, которая, по определению, являлась графиком квадратного трехчлена. Здесь мы дадим другое (геометрическое) определение параболы.
Определение 12.7 Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.
Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса  опустим перпендикуляр
опустим перпендикуляр  на директрису
на директрису  . Начало координат
. Начало координат  расположим на середине отрезка
расположим на середине отрезка  , ось
, ось  направим вдоль отрезка
направим вдоль отрезка  так, чтобы ее направление совпадало с направлением вектора
так, чтобы ее направление совпадало с направлением вектора  . Ось
. Ось  проведем перпендикулярно оси
проведем перпендикулярно оси  (рис. 12.15).
(рис. 12.15).
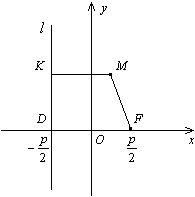
Рис.12.15.
Теорема 12.4 Пусть расстояние между фокусом 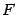 и директрисой
и директрисой 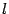 параболы равно
параболы равно 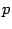 . Тогда в выбранной системе координат парабола имеет уравнение
. Тогда в выбранной системе координат парабола имеет уравнение
|
| (12.10) |
Доказательство. В выбранной системе координат фокусом параболы служит точка 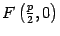 , а директриса имеет уравнение
, а директриса имеет уравнение  (рис. 12.15).
(рис. 12.15).
Пусть 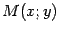 -- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим
-- текущая точка параболы. Тогда по формуле (10.4) для плоского случая находим
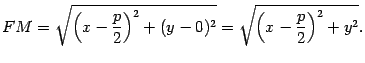
Расстоянием от точки  до директрисы
до директрисы 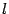 служит длина перпендикуляра
служит длина перпендикуляра  , опущенного на директрису из точки
, опущенного на директрису из точки  . Из рисунка 12.15 очевидно, что
. Из рисунка 12.15 очевидно, что 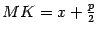 . Тогда по определению параболы
. Тогда по определению параболы 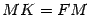 , то есть
, то есть
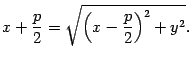
Возведем обе части последнего уравнения в квадрат:
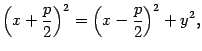
откуда
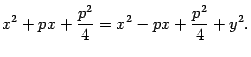
После приведения подобных членов получим уравнение (12.10).
Уравнение (12.10) называется каноническим уравнением параболы.
Предложение 12.4 Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью 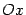 .
.
Доказательство. Проводится так же, как и доказательство (предложения 12.1).
Точка пересечения оси симметрии с параболой называется вершиной параболы.
Если переобозначить переменные 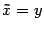 ,
, 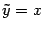 , то уравнение (12.10) можно записать в виде
, то уравнение (12.10) можно записать в виде
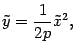
который совпадает с обычным уравнением параболы в школьном курсе математики. Поэтому параболу нарисуем без дополнительных исследований (рис. 12.16).
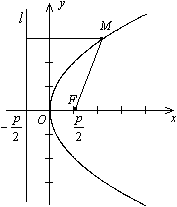
Рис.12.16.Парабола

Лекция 1. Геометрические векторы. Линейные операции с векторами. Скалярное, векторное, смешанное произведение векторов.
Сначала вспомним известные из школьной программы определения и свойства геометрических векторов.
Определение. Геометрическим вектором называется направленный отрезок.
Обозначаем:  , А — начало, B — конец вектора.
, А — начало, B — конец вектора.

Геометрические векторы также обозначают одной буквой:  и т.п.
и т.п.
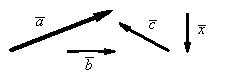
Определение. Длина вектора 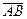 — расстояние между точками A и B.
— расстояние между точками A и B.
Обозначаем: 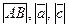 и т.п.
и т.п.
Определение. Два вектора называются равными, если они коллинеарны (лежат на параллельных прямых), одинаково направлены и их длины равны.
Обозначаем:  .
.
Определение. Два вектора называются противоположными, если они коллинеарны, равны по длине и противоположно направлены. Обозначаем: 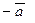 .
.

Определение. Нулевым называется вектор, имеющий нулевую длину. Направление нулевого вектора не определено. Обозначаем: 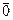 .
.
Определение. Суммой векторов 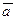 и
и 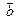 называется вектор
называется вектор  , определенный на рисунке (правило параллелограмма или правило треугольника). Обозначаем:
, определенный на рисунке (правило параллелограмма или правило треугольника). Обозначаем: 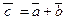 .
.

Определение. Произведением вектора 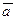 на число
на число  называется вектор длины
называется вектор длины 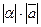 , коллинеарный вектору
, коллинеарный вектору 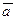 , направление которого при
, направление которого при  совпадает с направлением вектора
совпадает с направлением вектора 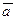 , а
, а  — противоположно направлению вектора
— противоположно направлению вектора 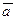 .
.

Определение. Ортом вектора 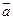 называется вектор единичной длины, направление которого совпадает с направлением вектора
называется вектор единичной длины, направление которого совпадает с направлением вектора 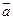 .
.
Обозначаем: 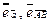 и т.п. Понятно, что
и т.п. Понятно, что 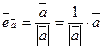 .
.
Определение. Операции сложения векторов и умножение вектора на число называются линейными операциями с векторами.
Известно (нетрудно доказать), что для линейных операций с векторами справедливо:
-
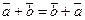 ;
; -
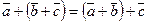 ;
; -
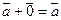 ;
; -
 ;
; -
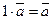 ;
; -
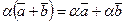 ;
; -
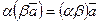 ;
; -
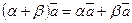 .
.
Равенства 1-8 справедливы для произвольных векторов  и для любых чисел
и для любых чисел 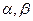 .
.
Декартовы координаты. Координаты вектора. Линейные операции с векторами в координатной форме
Вспомним, как определяются декартовы координаты точки в пространстве: 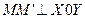 ,
, 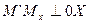 ,
, 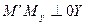 ,
, 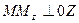 ,
, 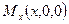 ,
, 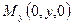 ,
, 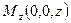 —
— 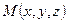 .
.

Единичные векторы координатных осей обозначаем 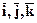 или
или 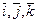 :
:

Координаты вектора 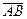 :
: 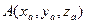 ,
, 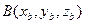 ,
, 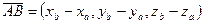 .
.
Обозначаем: 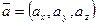 ,
, 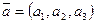 и т.п.
и т.п.
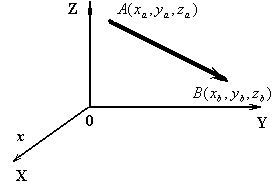
Напомним, что координаты вектора — это ортогональные проекции вектора на координатные оси: если 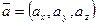 , то
, то 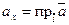 ,
, 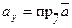 ,
, 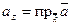 и
и 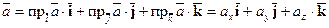 .
.
Легко видеть (по свойствам операций сложения векторов и умножения вектора на число), что если 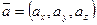 ,
, 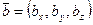 , то
, то 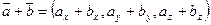 и
и 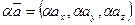 .
.
Действительно:
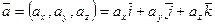 ,
, 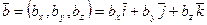 и
и 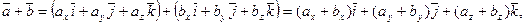 т.е.
т.е. 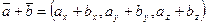 ;
;
аналогично и 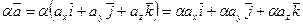 , т.е.
, т.е. 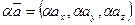 .
.
Длина вектора: если 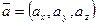 , то
, то 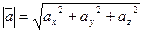 .
.
Определение. Вектор  называется радиусом-вектором точки A:
называется радиусом-вектором точки A:
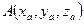 ,
, 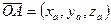
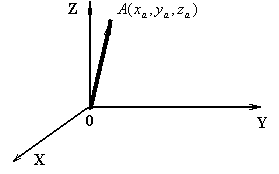
Пространство R3 арифметических векторов
Определение. Трехмерным арифметическим вектором называется упорядоченная совокупность 3 чисел. Обозначается 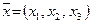 . Числа
. Числа 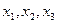 называются компонентами арифметического вектора.
называются компонентами арифметического вектора.
Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число: для любых 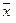 и
и  и любого числа
и любого числа  —
— 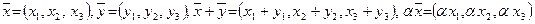 ,
,
Вектор 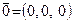 называется нулевым вектором, а вектор
называется нулевым вектором, а вектор 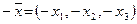 — противоположным вектором для вектора
— противоположным вектором для вектора 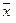 .
.
Определение. Множество трехмерных арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов R3.
Очевидно, что для любых 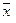 ,
,  ,
, 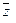 из Rn и любых чисел α, β справедливо:
из Rn и любых чисел α, β справедливо:
1. 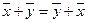 , сложение коммутативно;
, сложение коммутативно;
2. 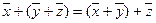 ,сложение ассоциативно;
,сложение ассоциативно;
3. 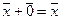 ;
;
4. 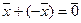 ;
;
5. 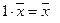 ;
;
6. 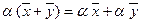 , умножение на число дистрибутивно относительно сложения векторов;
, умножение на число дистрибутивно относительно сложения векторов;
7. 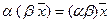 , умножение на число ассоциативно;
, умножение на число ассоциативно;
8. 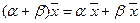 , умножение вектора на число дистрибутивно относительно сложения чисел.
, умножение вектора на число дистрибутивно относительно сложения чисел.
Мы видим, что операции сложения и умножения геометрических и трехмерных арифметических векторов имеют одинаковые свойства. Тогда можно проделать такое сопоставление:
Выберем в трехмерном геометрическом пространстве декартову систему координат. Тогда для каждого геометрического вектора 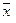 однозначно определены координаты
однозначно определены координаты 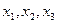 :
: 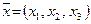 , что означает
, что означает  , причем, как показано выше,
, причем, как показано выше, 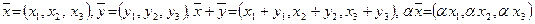 .
.
Это означает, что любой геометрический вектор можно рассматривать как трехмерный арифметический вектор, а пространство геометрических векторов можно изучать как пространство трехмерных арифметических векторов.
Деление отрезка в заданном отношении
Определение. Рассмотрим отрезок AB. Говорят, что точка M , принадлежащая отрезку AB делит его в отношении 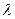 , если
, если 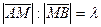 .
.

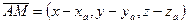 ,
, 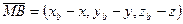 . По известному свойству проекций если
. По известному свойству проекций если 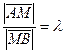 , то
, то  , т.е.
, т.е. 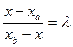 и
и 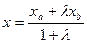 ; аналогично
; аналогично 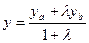 ,
, 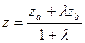 .
.
Точка  делит отрезок
делит отрезок  ,
,
 ,
,  в отношении
в отношении 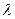 .
.
В частности, точка 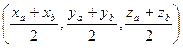 делит отрезок
делит отрезок  ,
,
 ,
,  пополам (
пополам ( 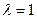 ).
).
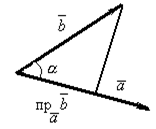
Скалярное произведение векторов
Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначаем: 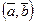 ,
, 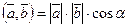 .
.
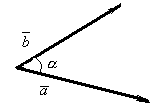
Поскольку 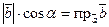 и
и 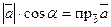 , то
, то 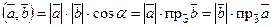
Свойства скалярного произведения. Нетрудно показать, что для произвольных векторов  ,
,  и
и 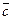 , и для любого числа
, и для любого числа 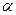 справедливо:
справедливо:
1. 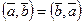 ;
;
2. 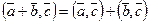 ;
;
3. 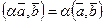 ;
;
4.  , причем
, причем 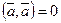 тогда и только тогда, когда
тогда и только тогда, когда 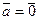 .
.
Доказательства свойств 1, 3 и 4 очевидно следуют из определения. Докажем свойство 2: 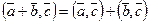 .
.
Действительно: 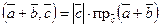 , но по известному свойству проекций
, но по известному свойству проекций  , тогда
, тогда 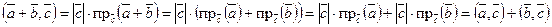 , что и требовалось доказать.
, что и требовалось доказать.
Из свойств 1- 4 можно вывести весьма важные и полезные следствия:
1. 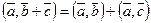 ;
;
2. 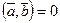 , тогда и только тогда, когда векторы
, тогда и только тогда, когда векторы 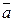 и
и  ортогональны (поскольку направление нулевого вектора не определено, его можно считать ортогональным любому вектору);
ортогональны (поскольку направление нулевого вектора не определено, его можно считать ортогональным любому вектору);
3. 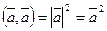 ; выражение
; выражение 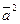 называют скалярным квадратом вектора;
называют скалярным квадратом вектора;
4. если 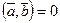 для любого вектора
для любого вектора 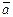 , то вектор
, то вектор  — нулевой, т.е. из
— нулевой, т.е. из  следует
следует 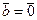 ;
;
5. если 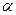 — угол между векторами
— угол между векторами 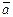 и
и  , то
, то 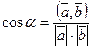 ;
;
6. если векторы 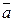 и
и  заданы своими координатами в некоторой декартовой системе координат:
заданы своими координатами в некоторой декартовой системе координат:  ,
, 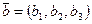 , то
, то 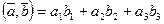 .
.
Следствия 1, 2 , 3 и 5 очевидно следуют из определения скалярного произведения. Докажем свойство 4.
Пусть 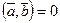 для любого вектора
для любого вектора 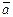 . Значит, и для
. Значит, и для  , тогда
, тогда  , но
, но 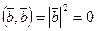 , следовательно,
, следовательно, 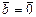 .
.
Докажем свойство 6 — вычисление скалярного произведения в координатах.
Если векторы 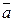 и
и  заданы своими координатами в некоторой декартовой системе координат:
заданы своими координатами в некоторой декартовой системе координат: 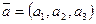 ,
, 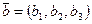 , то
, то  ,
, 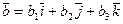 . Вычислим
. Вычислим 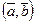 :
:
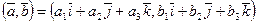 , из свойства 2 и следствия 1 следует:
, из свойства 2 и следствия 1 следует:

из свойства 3 и следствия 2 следует:
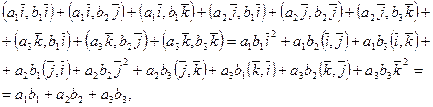
поскольку  .
.
Доказано, что 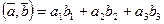 .
.
Скалярное произведение векторов можно использовать для вычисления углов между векторами: если 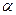 — угол между векторами
— угол между векторами 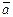 и
и  , то
, то 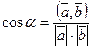 .
.
Равенство нулю скалярного произведения векторов — признак ортогональности векторов: 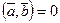 , тогда и только тогда, когда векторы
, тогда и только тогда, когда векторы 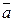 и
и  ортогональны.
ортогональны.
Определители 2-го и 3-го порядка
Определение. Определителем 2-го порядка называется число, вычисленное по квадратной таблице из 4-х чисел следующим образом:
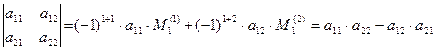 .
.
Определение. Определителем 3-го порядка называется число, вычисленное по квадратной таблице из 9-ти чисел следующим образом:
 .
.
Векторное произведение векторов
Определение. Векторным произведением векторов 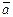 и
и  (обозначаем его
(обозначаем его 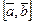 ) называется вектор, который определяется следующим образом:
) называется вектор, который определяется следующим образом:
o 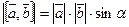 ,
, 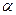 — угол между векторами
— угол между векторами 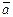 и
и  ; (определили длину вектора
; (определили длину вектора  );
);
o вектор 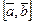 ортогонален вектору
ортогонален вектору 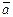 и вектору
и вектору  ; (определили положение вектора
; (определили положение вектора  в пространстве);
в пространстве);
o векторы 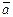 ,
,  и
и 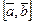 образуют правую тройку; (определили направление вектора
образуют правую тройку; (определили направление вектора  ).
).

Правая тройка: из конца вектора 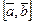 поворот от вектора
поворот от вектора 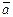 к вектору
к вектору  видится против часовой стрелки. Правую тройку хорошо «моделировать тремя первыми пальцами правой руки.
видится против часовой стрелки. Правую тройку хорошо «моделировать тремя первыми пальцами правой руки.
Важный пример.  ,
,
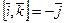 ,
,
 .
.
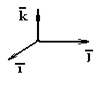
Свойства векторного произведения. Нетрудно показать, что для произвольных векторов 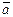 ,
,  и
и 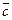 , и для любого числа
, и для любого числа 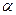 справедливо:
справедливо:
1. 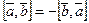 ;
;
2.  ;
;
3. 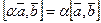 ;
;
4. 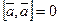 .
.
Доказательства свойств 1, 3 и 4 очевидно следуют из определения. Свойство 2 докажем чуть позже.
Из свойств 1- 4 можно вывести весьма важные и полезные следствия:
1. 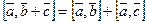 ;
;
2. 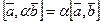 ;
;
3. 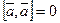 , тогда и только тогда, когда векторы
, тогда и только тогда, когда векторы 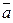 и
и  коллинеарны (лежат на параллельных прямых; нулевой вектор полагают коллинеарным любому вектору);
коллинеарны (лежат на параллельных прямых; нулевой вектор полагают коллинеарным любому вектору);
4. длина векторного произведения ( 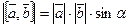 ,
,  — угол между неколлинеарными векторами
— угол между неколлинеарными векторами 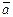 и
и  ) равна площади параллелограмма, построенного на векторах
) равна площади параллелограмма, построенного на векторах  и
и  как на сторонах;
как на сторонах;
5. если векторы  и
и  заданы своими координатами в некоторой декартовой системе координат:
заданы своими координатами в некоторой декартовой системе координат: 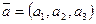 ,
,  , то
, то  .
.
Следствия 1- 4 очевидно следуют из определения векторного произведения и его свойств. Докажем свойство 5. Доказательство совершенно аналогично доказательству формулы вычисления скалярного произведения в координатах.
Если векторы  и
и  заданы своими координатами в некоторой декартовой системе координат:
заданы своими координатами в некоторой декартовой системе координат: 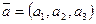 ,
, 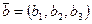 , то
, то  ,
, 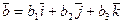 . Вычислим
. Вычислим  :
:
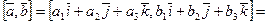
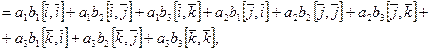
а поскольку (см. важный пример):
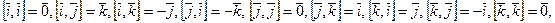 то имеем:
то имеем:
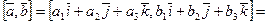

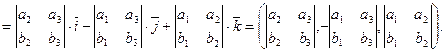
Для вычисления векторного произведения в координатах используют мнемоническую запись:
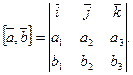
Векторное произведение векторов можно использовать для вычисления площадей параллелограммов и треугольников: углов между векторами: 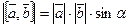 ,
,  — угол между неколлинеарными векторами
— угол между неколлинеарными векторами  и
и  если
если 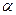 — угол между векторами
— угол между векторами 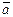 и
и  ,
, 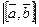 — площадь параллелограмма,
— площадь параллелограмма, 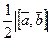 — площадь треугольника.
— площадь треугольника.
Равенство нулю векторного произведения векторов — признак коллинеарности векторов: 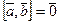 , тогда и только тогда, когда векторы
, тогда и только тогда, когда векторы 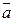 и
и 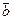 коллинеарны.
коллинеарны.
Смешанное произведение векторов
Определение. Смешанное произведение векторов 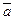 ,
, 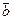 и
и 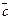 (обозначаем его
(обозначаем его 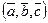 ) определяется равенством
) определяется равенством 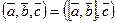 , т.е. равно скалярному произведению векторов
, т.е. равно скалярному произведению векторов 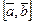 и
и 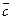 .
.
Свойства смешанного произведения. Понятно, что свойства смешанного произведения — это свойства скалярного произведения двух векторов, а поскольку первый из сомножителей, 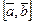 , векторное произведение, то получим суперпозицию свойств векторного и скалярного произведений.
, векторное произведение, то получим суперпозицию свойств векторного и скалярного произведений.
Например: 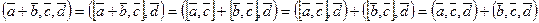 .
.
Рассмотрим только некоторые, наиболее интересные с нашей точки зрения свойства.
Признак компланарности векторов. Векторы, лежащие в одной плоскости (параллельные одной плоскости) называются компланарными векторами.
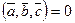 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 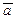 ,
, 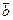 и
и 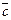 компланарны.
компланарны.
Действительно, если 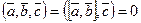 , то векторы
, то векторы 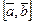 и
и 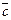 — ортогональны. Но вектор
— ортогональны. Но вектор 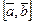 ортогонален векторам
ортогонален векторам 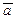 и
и 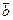 . Это означает, что у векторов
. Это означает, что у векторов 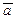 ,
, 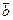 и
и 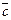 есть общий перпендикуляр, а это означает, что векторы
есть общий перпендикуляр, а это означает, что векторы 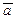 ,
, 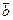 и
и 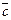 лежат в одной плоскости (параллельны одной плоскости) — компланарны. Наоборот: если векторы что векторы
лежат в одной плоскости (параллельны одной плоскости) — компланарны. Наоборот: если векторы что векторы 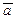 ,
, 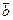 и
и 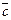 лежат в одной плоскости, то векторное произведение
лежат в одной плоскости, то векторное произведение 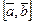 ортогонально этой плоскости, т.е. ортогонально всем векторам плоскости, т.е. ортогонально вектору
ортогонально этой плоскости, т.е. ортогонально всем векторам плоскости, т.е. ортогонально вектору 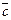 , т.е.
, т.е. 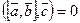 , или, что то же самое,
, или, что то же самое, 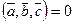 . Что и требовалось доказать.
. Что и требовалось доказать.
С помощью смешанного произведения можно вычислять объемы: 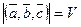 , V — объем параллелепипеда, построенного на векторах
, V — объем параллелепипеда, построенного на векторах 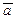 ,
, 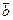 и
и 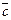 как на ребрах. Более того, если
как на ребрах. Более того, если 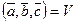 , то векторы
, то векторы 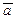 ,
, 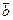 и
и 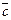 образуют правую тройку, если же
образуют правую тройку, если же 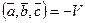 то векторы
то векторы 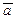 ,
, 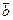 и
и 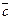 образуют левую тройку.
образуют левую тройку.
Действительно, 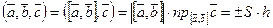 , где S — площадь основания параллелепипеда, h — высота параллелепипеда, а знак определяется направлением вектора
, где S — площадь основания параллелепипеда, h — высота параллелепипеда, а знак определяется направлением вектора 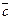 : «+» если вектор
: «+» если вектор 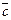 образует острый угол с плоскостью векторов
образует острый угол с плоскостью векторов 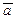 ,
, 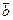 и
и
«–», если этот угол тупой; 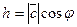 ,
, 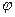 — угол между векторами
— угол между векторами 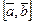 и
и 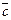 . См. рисунок.
. См. рисунок.

Ясно, что смешанное произведение позволяет вычислить объем тетраэдра, построенного на векторах 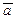 ,
, 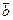 и
и 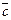 как на ребрах:
как на ребрах:  Здесь S — площадь основания тетраэдра (площадь треугольника, она равна половине
Здесь S — площадь основания тетраэдра (площадь треугольника, она равна половине 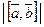 ), h —
), h —
высота тетраэдра (совпадает с высотой параллелепипеда).
См. рисунок.
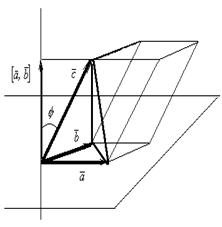
Связь смешанного произведения с объемом параллелепипеда позволяет доказать нетривиальное равенство: 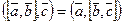 .
.
Действительно, легко видеть, что оба смешанные произведения равны объему одного и того же параллелепипеда (объему со знаком «–» если тройка левая). Нарисуйте соответствующую картинку и увидите.
Это последнее равенство позволяет доказать линейность векторного произведения. Посмотрите выше. Было обещано доказать
 ;
;
Действительно.  ,
,
т.е. 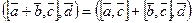 , откуда
, откуда 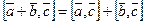 . Что и нужно было доказать.
. Что и нужно было доказать.
Вычислим смешанное произведение в координатах. Вспомните формулы для вычисления определителя 3-го порядка, формулы вычисления скалярного и векторного произведения в координатах.
Если векторы 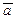 ,
, 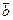 и
и 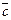 заданы своими координатами в некоторой декартовой системе координат:
заданы своими координатами в некоторой декартовой системе координат: 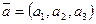 ,
, 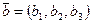 ,
, 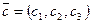 , то
, то 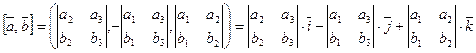 , а
, а
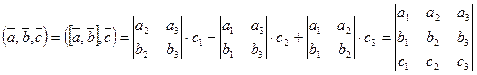
Смешанное произведение векторов можно использовать для вычисления объемов параллелепипедов:  , V — объем параллелепипеда, построенного на векторах
, V — объем параллелепипеда, построенного на векторах 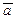 ,
, 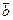 и
и 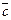 как на ребрах .
как на ребрах .
Если смешанное произведение положительно — векторы 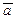 ,
, 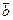 и
и 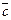 образуют правую тройку; иначе — левую.
образуют правую тройку; иначе — левую.
Равенство нулю смешанного произведения векторов — признак компланарности векторов: 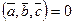 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 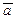 ,
, 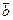 и
и 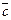 компланарны.
компланарны.
Дата: 2019-02-02, просмотров: 494.