Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

Рассмотрим систему m линейных алгебраических уравнений относительно n неизвестных :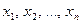

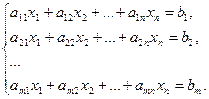
Определение. Решением системы называется совокупность n значений неизвестных 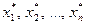, при подстановке которых  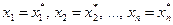все уравнения системы обращаются в тождества.

Определение. Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.

Напомним, что система линейных уравнений может быть записана в матричной форме:

,

где 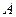— матрица системы, 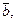— правая часть, — искомое решение,

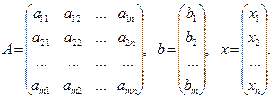
Необходимое и достаточное условие совместности системы линейных алгебраических уравнений

На вопрос о совместности системы линейных алгебраических уравнений отвечает следующая теорема.

Теорема (теорема Кронекера-Капелли). Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы.

Доказательство теоремы.

Необходимость. Система  совместна. Докажем, что .

Система  совместна — существуют такие числа , что

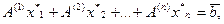
т.е. вектор-столбец правой части линейно выражается через столбцы 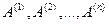 матрицы A. Это означает, что при добавлении столбца  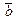число линейно независимых столбцов не увеличивается, т.е. . Необходимость доказана.

Достаточность. 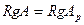. Докажем, что система  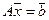совместна.

Пусть 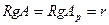. Это означает, что среди столбцов обеих матриц есть r линейно независимых столбцов, а все остальные линейно выражаются через эти r столбцов. Не умаляя общности, положим, что линейно независимы первые r столбцов 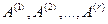. Тогда столбцы  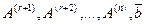— линейно зависимы и, следовательно, столбец  линейно выражается через : .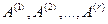

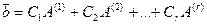Положим ,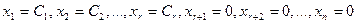

тогда

т.е. вектор 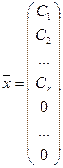 — решение системы ,

т.е. система 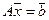 совместна. Теорема доказана.

Свойства решений систем линейных алгебраических уравнений

Используя свойства линейных операций с матрицами, нетрудно доказать, справедливость следующих утверждений.

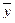1. Если  и  — два решения однородной системы 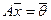, то при любых действительных числах α и β вектор  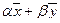— решение системы .

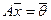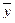2. Если  и  — два решения неоднородной системы , то вектор 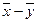 — решение приведенной однородной системы однородной .

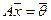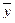3. Если  решение неоднородной системы , а  — решение однородной системы 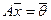, то вектор  — решение неоднородной системы .

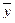Докажем, например, первое из этих свойств. Пусть  и  — два решения системы 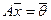, т. е.  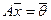и 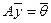 и пусть α и β любые действительные числа. Тогда 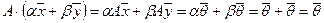, т.е. вектор  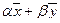— решение однородной системы.

Остальные утверждения докажите аналогично самостоятельно.

Структура общего решения неоднородной системы

Вспомним одно из свойств решений линейной неоднородной системы:

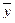Если  и  — два решения системы , то вектор 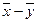 — решение приведенной однородной системы .

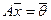Поскольку выражение  задает все решения однородной системы, то для любых двух решений  и 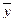 неоднородной системы справедливо

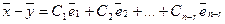 и, следовательно, выражение  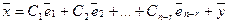позволяет вычислить любое решение неоднородной системы.

Таким образом доказана теорема о структуре общего решения линейной неоднородной системы.

Теорема о структуре общего решения неоднородной системы линейных алгебраических уравнений. Если ранг r матрицы неоднородной системы линейных уравнений меньше числа неизвестных n , то общее решение системы можно записать в виде

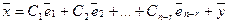
где 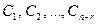— произвольные константы, а 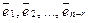— фундаментальная система решений приведенной однородной системы, 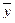— некоторое известное (частное) решение неоднородной системы.

Формулы Крамера. Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных

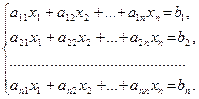
Обозначим: 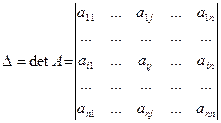 — определитель матрицы системы, и  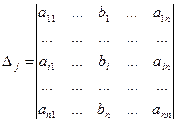— определитель матрицы, полученной из матрицы системы заменой j-го столбца столбцом правых частей.

Если определитель матрицы системы отличен от нуля, 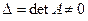, то решение системы

 

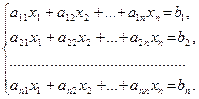
определяется равенствами: .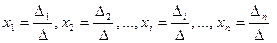

Докажем это утверждение. Пусть .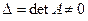

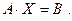Обозначим  и покажем, что  Вычислим

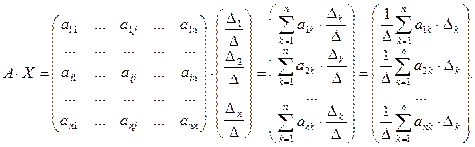
Вычислим определитель 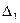 разложением по первому столбцу, определитель  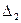— по второму, …,  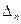 — по n-му:

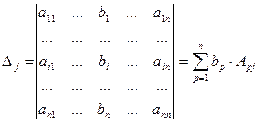, поскольку определитель  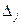отличается от  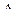только j-м столбцом. Тогда

 

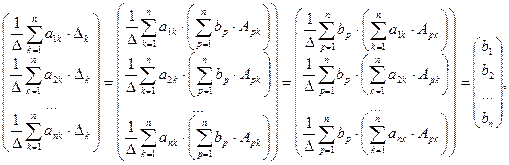
поскольку

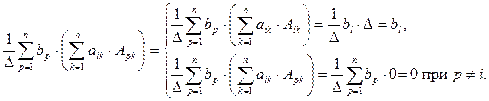
Т.е. 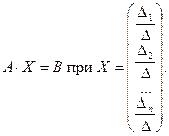 Формулы Крамера доказаны.

Замечание. Нетрудно, показать, что выражения 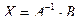 и 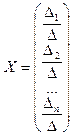 — две формы записи одного и того же равенства.

Действительно,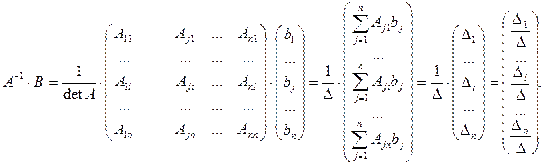

Лекция 6. Линейное пространство. Линейная зависимость системы векторов. Размерность, базис. Линейное подпространство. Примеры

 

Линейное пространство арифметических векторов Rⁿ

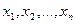Определение. Арифметическим вектором называется упорядоченная совокупность n чисел. Обозначается , числа  называются компонентами арифметического вектора.

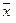Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число: для любых и 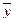и любого числа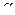

Определение. Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов­­ Rⁿ.

Вектор называется нулевым вектором, а вектор  — противоположным вектором для вектора .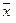

Для любых 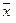, , 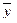 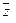из Rⁿ и любых чисел α , β справедливо:

1. 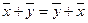, сложение коммутативно;

2. 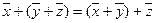, сложение ассоциативно;

3.

4.

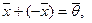
5. , умножение на число дистрибутивно относительно сложения элементов;

6. 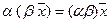, умножение на число ассоциативно;

7. , умножение вектора на число дистрибутивно относительно сложения чисел.

8.

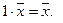
Примерами пространства арифметических векторов являются пространства геометрических векторов на плоскости, записанных в координатной форме.

Линейная зависимость и линейная независимость в Rⁿ

Определение. Линейной комбинацией векторов 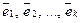 называется выражение 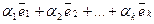, где коэффициенты линейной комбинации  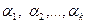— некоторые числа.

Определение. Говорят, что вектор 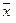 пространства Rⁿ линейно выражается через векторы 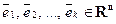, если его можно представить в виде линейной комбинации этих элементов 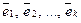, т.е. представить в виде .

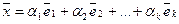Определение. Система 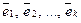 векторов из Rⁿ называется линейно независимой если из  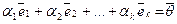следует равенство нулю всех коэффициентов , .

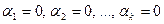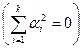Иными словами, линейная комбинация векторов равна нулю тогда и только тогда, когда все коэффициенты линейной комбинации равны нулю.

Определение. Система векторов, которая не является линейно зависимой, называется линейно независимой.

Иными словами, существуют такие коэффициенты линейной комбинации 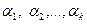, не все равные нулю , что .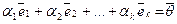

Или: линейная комбинация векторов может обратиться в нуль, хотя не все коэффициенты линейной комбинации равны нулю.

Пример. Исследуем на линейную зависимость векторы 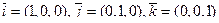 из R ³.

Составим линейную комбинацию векторов и приравняем ее нулю:

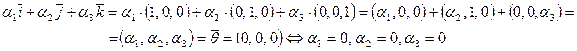
Т.е. линейная комбинация равна нулю тогда и только тогда, когда все ее коэффициенты нулевые — векторы  линейно независимы.

Пример. Исследуем на линейную зависимость систему векторов 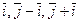 из R ³.

Составим линейную комбинацию векторов и приравняем ее нулю:

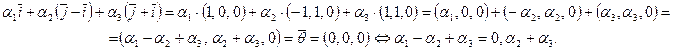Пусть, например, 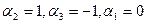, тогда 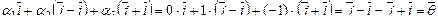, т.е. существует нулевая линейная комбинация с отличными от нуля коэффициентами — векторы  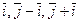— линейно зависимы.

Свойства линейно зависимых и линейно независимых систем функций

1. Любая система векторов, содержащая нулевой вектор линейно зависима.

2. Любая система векторов, содержащая пару взаимно противоположных векторов — линейно зависима.

3. Любая система векторов, содержащая два равные вектора — линейно зависима.

4. Любая подсистема линейно независимой системы векторов — линейно независима.

5. Если некоторая подсистема системы векторов линейно зависима, то и вся система — линейно зависима.

Докажем первое из этих утверждений: любая система векторов, содержащая нулевой вектор линейно зависима. Рассмотрим произвольную систему векторов 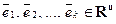 и добавим к ней нулевой вектор: 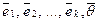. Тогда : 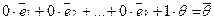, т.е. равна нулю линейная комбинация с одним ненулевым коэффициентом — векторы линейно зависимы, ч.т.д.

Остальные утверждения доказываются аналогично. Докажите сами.

Необходимое и достаточное условие линейной зависимости системы векторов в Rⁿ

Справедливо следующее утверждение.

Теорема (Необходимое и достаточное условие линейной зависимости системы векторов). Система 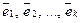 векторов из Rⁿ линейно зависима тогда и только тогда, когда хотя бы один вектор системы векторов  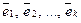из Rⁿ линейно выражается через остальные векторы системы.

Доказательство теоремы. Необходимость. Дано: векторы 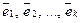 линейно зависимы. Докажем, что хотя бы один из них линейно выражается через остальные .

Векторы 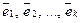 линейно зависимы. Это означает, что существуют такие коэффициенты линейной комбинации 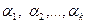, не все равные нулю, что .

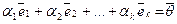Не умаляя общности, предположим, что именно 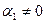. Тогда из  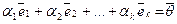следует:  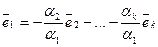— вектор  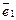линейно выражается через 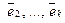. Необходимость доказана.

Достаточность. Дано: один из векторов системы 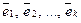 линейно выражается через остальные. Докажем, что векторы линейно зависимы.

Действительно, не умаляя общности, положим, что вектор 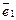 линейно выражается через 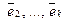: 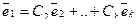. Если все , то  и векторы  линейно зависимы (см. св-во 1). Если же среди  есть хоть одно отличное от нуля число, то 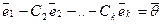 — имеем нулевую линейную комбинацию, не все коэффициенты которой равны нулю — система векторов  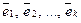линейно зависима. Достаточность доказана. Теорема доказана.

Базис в Rⁿ. Координаты вектора в заданном базисе. Линейные операции в координатной форме

Определение. Система векторов из R ⁿ образует базис в R ⁿ если:

1. система векторов упорядочена;

2. система векторов линейно независима;

3. любой вектор из R ⁿ линейно выражается через векторы системы.

Иными словами, линейно независимая упорядоченная система векторов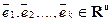

Образует базис в R ⁿ если любой вектор 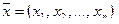 из Rⁿ может быть представлен в виде .

Определение. Выражение  называется разложением вектора в базисе 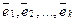, а числа  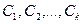называются координатами вектора  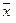в базисе .

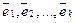Пример. Нетрудно доказать, что система арифметических векторов

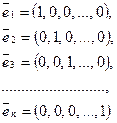
линейно независима (см. пример с 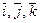) и что для любого  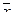из Rⁿ система векторов  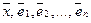линейно зависима, поскольку любой вектор  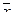линейно выражается через 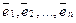: . Т.е. в Rⁿ существует базис, состоящий из n векторов. Базис  называется естественным базисом в Rⁿ, и компоненты вектора 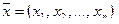— его координаты в естественном базисе.

Справедливо следующее утверждение.

Теорема (о единственности разложения вектора в базисе). Для любого вектора 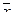 из Rⁿ разложение  вектора в базисе 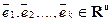 единственно.

Доказательство теоремы. «От противного». Пусть не так. Т.е. векторы 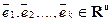 образуют базис в Rⁿ , помимо разложения , существует разложение 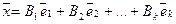 и не все коэффициенты C_i , B_i совпадают.

Тогда 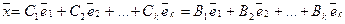, и, следовательно, 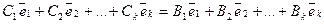, откуда .

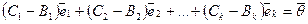Но векторы 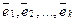 образуют базис, — они линейно независимы, и, следовательно, 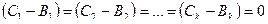, т.е. — все коэффициенты разложений соответственно равны — разложения совпадают. Теорема доказана.

Следствие. Координаты вектора в заданном базисе определяются единственным образом.

Теорема. В пространстве Rⁿ существует базис из n векторов.

Действительно, этот базис — естественный базис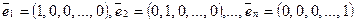

Линейные операции в координатной форме

Пусть векторы  образуют базис в Rⁿ. Тогда для любых двух векторов  и

 из Rⁿ однозначно определены разложения , 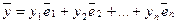. Тогда из свойств арифметических операций в Rⁿ следует:

 и

для любого числа : .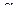

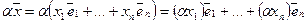Иными словами, координаты суммы векторов в заданном базисе равны сумме соответствующих координат слагаемых, а координаты произведения вектора на число — произведению соответствующих координат вектора на число.

Линейные подпространства в Rⁿ, размерность подпространства, базис в подпространстве

Определение. Множество L векторов из Rⁿ , такое, что для любых 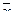 и 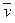из L и любого числа α справедливо 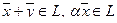, называется линейным подпространством в Rⁿ.

Пример. Множество L арифметических векторов из Rⁿ, у которых последние компоненты — нулевые, образует линейное подпространство в Rⁿ:

 

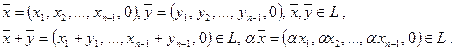
Нетрудно доказать, что для любого линейного подпространства справедливо:

1. если вектор 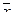 принадлежит линейному подпространству L, то и вектор  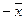принадлежит линейному подпространству L;
2. любое линейное подпространство содержит нулевой элемент.

Действительно, пусть 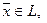но тогда и 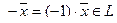, и, следовательно, .

Утверждение. Пространство ­Rⁿ само является линейным подпространством в Rⁿ.

Это утверждение очевидно, поскольку сумма любых двух векторов из Rⁿ и произведение любого вектора из Rⁿ на любое число принадлежат Rⁿ.

Определение. Число k называется размерностью линейного подпространства L , если в L существует система из k линейно независимых векторов, а любые k +1 вектора — линейно зависимы. Обозначаем dimL = k .

Нетрудно доказать следующее утверждение.

Теорема. В k -мерном линейном подпространстве существует базис их k векторов.

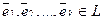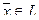Доказательство теоремы. Действительно, если dimL = k, то существует система из k линейно независимых векторов , а любая система из k+1 вектора  — линейно зависима, но тогда любой вектор   линейно выражается через векторы : , т.е. 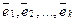  — базис в L.

Справедливы также следующие утверждения (оставим их без доказательства).

Теорема. Любая упорядоченная система из k линейно независимых векторов k -мерного линейного подпространства является базисом в этом подпространстве.

Теорема. Размерность линейного подпространства равна числу векторов в базисе этого подпространства.

Отсюда следует: dim ( Rⁿ ) = n.

Действительно, в пространстве Rⁿ есть базис из n векторов — естественный базис в Rⁿ.

Пример. Размерность линейного подпространства L арифметических векторов из Rⁿ, у которых последние компоненты — нулевые, равна n – 1.

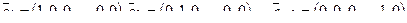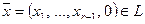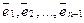Действительно, векторы  — очевидно, принадлежат L и линейно независимы. Покажем, что они образуют базис в L. Для произвольного вектора  имеет место разложение справедливо: , т.е. векторы  образуют базис в L. В этом базисе n-1 вектор, следовательно, dimL = n –1.

Тогда можно использовать другое определение базиса.

Определение. Любая упорядоченная линейно независимая система из k векторов k -мерного линейного подпространства L образует базис этого линейного подпространства L .

Это означает, что если dimL = k и арифметические векторы 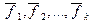 из L линейно независимы, то для любого 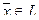существует единственный набор чисел  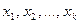таких, что .

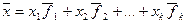Метрические соотношения в Rⁿ

Определение. Если каждой паре векторов 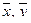из пространства Rⁿ поставлено в соответствие действительное число 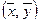, так, что для любых  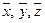из Rⁿ и любого действительного числа  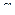справедливы следующие равенства:

1.

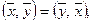
2.

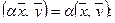
3.

4. 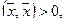при 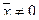, , 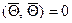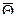— нулевой вектор,

то говорят, что в пространстве Rⁿ определено скалярное произведение .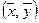

Пример. Легко проверить, что изученное в разделе «аналитическая геометрия» скалярное произведение известное из школьного курса скалярное произведение в трехмерном пространстве геометрических векторов (в R ³) является скалярным произведением в определенном выше смысле.

Пример. Рассмотрим пространство арифметических векторов R ² ={X=(x₁, x₂)}. Определим скалярное произведение следующим образом:

(X, Y) = 2x₁y₁ + 3x₂y₂.

Легко убедиться, что для определенного таким образом скалярного произведения справедливы аксиомы 1. — 4.:

(X, Y) = 2x₁y₁ + 3x₂y₂ = 2y₁x₁ + 3y₂x₂ = (Y, X),

(aX, Y) = 2(ax₁)y₁ + 3(ax₂)y₂ = a(2y₁x₁ + 3y₂x₂) = a (X, Y),

(X+Y, Z) = 2(x₁+y₁)z₁ + 3(x₂+y₂)z₂ = (2x₁z₁ + 3x₂z₂) + (2y₁z₁ + 3y₂z₂) = (X, Z) + (Y, Z),

(X , X) = 2x₁x₁ + 3x₂x₂ = 2x₁² + 3x₂² >0 если 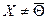, если же X = (0, 0), то (X , X) = 0.

Вернемся к пространству арифметических векторов Rⁿ = { }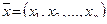

Определим в Rⁿ  естественное скалярное произведение: каждой паре векторов 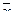 и 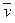из этого пространства поставим в соответствие действительное число 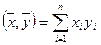. Нетрудно доказать, что для любых векторов 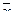,  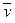и 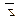и любого действительного числа  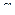для 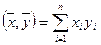справедливо:

1.

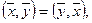
2.

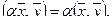
3.

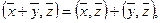
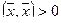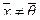4.  при , и 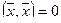 тогда и только тогда, когда 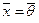, 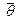— нулевой вектор.

 Пространство арифметических векторов Rⁿ  с определенным в нем естественным скалярным произведением называют евклидовым пространством арифметических векторов и иногда обозначают Eⁿ.

Свойства скалярного произведения. Неравенство Коши-Буняковского

Теорема (неравенство Коши-Буняковского). Для любых векторов 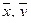из пространства Rⁿ справедливо следующее неравенство .

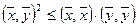Доказательство теоремы. Возьмем произвольное число 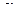 и рассмотрим 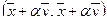. По последнему свойству скалярного произведения для любых векторов 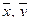и любого числа  справедливо: 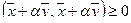. С другой стороны, 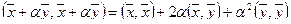, т.е. . Выражение в левой части неравенства — квадратный трехчлен относительно 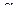. Он неотрицателен тогда и только тогда, когда дискриминант . Из последнего неравенства немедленно следует неравенство Коши-Буняковского: , . 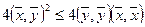Теорема доказана.

Метрические соотношения в Rⁿ

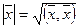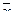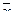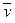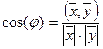Определение. Число  называется длиной вектора ;  число  — расстоянием между векторами  и ; угол , косинус которого   — углом между векторам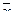и  и .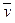

Если в Rⁿ скалярное произведение определено формулой 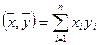, то для любых 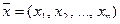,  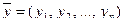из Rⁿ справедливо:

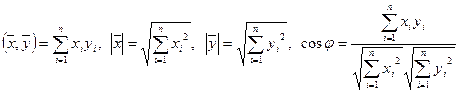
Ортогональность, ортогональные системы, ортонормированные базисы

Определение. Векторы  и 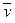из пространства Rⁿ называются ортогональными, если

Определение. Система 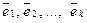 векторов из пространства Rⁿ называется ортогональной, если векторы системы попарно ортогональны.

Теорема (о линейной независимости ортогональных систем). Ортогональная система векторов линейно независима.

Доказательство теоремы.

Предположим противное: векторы 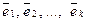 попарно ортогональны, но они линейно зависимы. Тогда один из векторов линейно выражается через остальные. Например, пусть это первый вектор: ,  (ясно, что речь идет о ненулевых векторах). Тогда 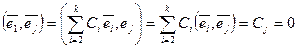, для всех j = 2, 3, …, k, т.е. 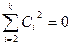. Полученное противоречие доказывает теорему.

 Определение. Система векторов из пространства Rⁿ называется ортонормированной, если векторы системы попарно ортогональны и имеют единичную длину.

Определение. Базис пространства Rⁿ называется ортонормированным базисом, если образующие его векторы попарно ортогональны и имеют единичную длину.

В пространстве Rⁿ в естественном скалярном произведении 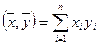естественный базис — ортонормированный базис.

Подпространство строк и подпространство столбцов прямоугольной матрицы

 

Рассмотрим прямоугольную матрицу A_{m , n}, у которой m строк и n столбцов:

.

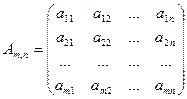Её строки — 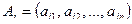 —являются векторами из Rⁿ,

А столбцы — 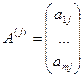 — являются векторами из R^m.

Понятно, что множество строк матрицы A_{m , n} , к которому добавили все строки, которые могут быть получены при элементарных преобразованиях матрицы (исключая транспонирование) — линейное подпространство в Rⁿ.

А аналогично образованное множество столбцов — линейное подпространство в R^m.

Это означает, что мы можем говорить о линейной зависимости и о линейной независимости строк и столбцов матрицы, о размерности подпространства строк и подпространства столбцов матрицы, о базисах в соответствующих подпространствах.