Индекс – обобщенная характеристика сравнения двух совокупностей, образуемых непосредственно несопоставимыми единицами.
Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс, который характеризует изменение во времени (или в пространстве) отдельных элементов той или иной совокупности. Так, индивидуальный индексы цены рассчитывается по формуле:
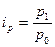 ,
,
где 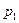 – цена товара в текущем периоде;
– цена товара в текущем периоде; 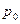 – цена в базисном периоде. Оценить изменение объемов продажи товара в натуральных единицах измерения позволяет индивидуальный индекс физического объема реализации:
– цена в базисном периоде. Оценить изменение объемов продажи товара в натуральных единицах измерения позволяет индивидуальный индекс физического объема реализации:
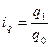 ,
,
где 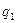 – количество товара, реализованное в текущем периоде;
– количество товара, реализованное в текущем периоде; 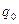 – количество товара, реализованное в базисном периоде. Изменение объема реализации товара в стоимостном выражении отражает индивидуальный индекс товарооборота:
– количество товара, реализованное в базисном периоде. Изменение объема реализации товара в стоимостном выражении отражает индивидуальный индекс товарооборота:
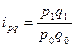 .
.
Если изучаются не отдельные единицы совокупности, а их группы или все без исключения единицы совокупности, то рассчитывают групповые и общие (сводные) индексы соответственно.
Общие индексы по методам построения подразделяются на агрегатные и средние из индивидуальных.
Агрегатные индексы – исходная (основная) форма общих индексов. Они используются для изучения динамики совокупности непосредственно несопоставимых явлений. Несопоставимость при этом преодолевается приведением элементов к единой форме путем введения в формулы дополнительного сомножителя, соизмерителя или веса индекса.
Основные формулы агрегатных индексов:
· индекс физического объема товарооборота (количества проданных товаров): 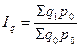 ;
;
· индекс цен на товары по методике Э. Ласпейреса: 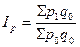 ;
;
· индекс цен на товары по методике Г. Паше: 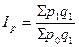 ;
;
· индекс товарооборота (выручки от продажи): 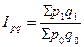 .
.
Если индекс цен построен по методике Г. Пааше, то индексы взаимосвязаны следующим образом: 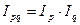 .
.
Разность между числителем и знаменателем соответствующих индексов показывает абсолютное изменение товарооборота ( 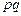 ) за счет отдельных факторов:
) за счет отдельных факторов:
· за счет изменения количества продаж: 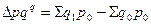 ;
;
· за счет изменения цен (по метод. Э. Ласпейреса): 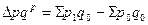 ;
;
· за счет изменения цен (по метод. Г. Паше): 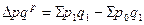 ;
;
· за счет совместного действия обоих факторов: 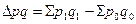 .
.
Указанные абсолютные приросты взаимосвязаны следующим образом: 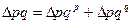 .
.
Часто отсутствие необходимой информации не позволяет вычислить общие индексы в агрегатной форме. В таком случае решить указанную проблему позволят преобразования агрегатных индексов в средние индексы из индивидуальных.
Средний арифметический индекс физического объема товарооборота:
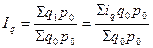 ,
,
где 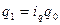 (исходя из того, что
(исходя из того, что 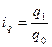 ).
).
Средний гармонический индекс цен:
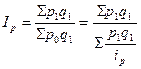 ,
,
где 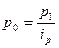 (исходя из того, что
(исходя из того, что 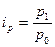 ).
).
Задача 2.5.1
Имеются следующие данные о продаже товаров на рынке города:
| Товары | Единица измерения | Количество, тыс. ед. | Цена, руб. | ||
| базисный период | отчетный период | базисный период | отчетный период | ||
| А Б | кг л | 1000 2000 | 750 1800 | 15 5 | 20 6 |
Определить: индивидуальные индексы объемов продаж в натуральном выражении, цен, товарооборота; общий индекс физического объема, общие индексы цен (по двум методикам); общий индекс товарооборота; абсолютные приросты товарооборота за счет изменения объемов продаж, цен и за счет совместного действия обоих факторов. Показать взаимосвязь между общими индексами и между абсолютными приростами.
Решение.
1. Индивидуальные индексы по товару «А»:
· индивидуальный индекс объема продаж: 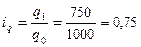 , или 75 % (снижение на 25 %);
, или 75 % (снижение на 25 %);
· индивидуальный индекс цены: 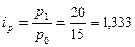 , или 133,3 % (рост на 33,3 %);
, или 133,3 % (рост на 33,3 %);
· индивидуальный индекс товарооборота:
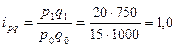 , или 100 % (без изменения).
, или 100 % (без изменения).
Взаимосвязь индексов: 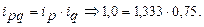
2. Индивидуальные индексы по товару «Б»:
· индивидуальный индекс объема продаж: 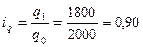 , или 90 % (снижение на 10 %);
, или 90 % (снижение на 10 %);
· индивидуальный индекс цены: 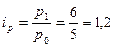 , или 120 % (рост на 20 %);
, или 120 % (рост на 20 %);
· индивидуальный индекс товарооборота: 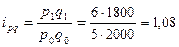 , или 108 % (рост на 8 %).
, или 108 % (рост на 8 %).
Взаимосвязь индексов: 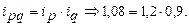
3. Общий индекс физического объема.
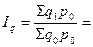
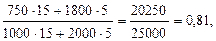 или 81 %.
или 81 %.
Таким образом, количество проданных товаров по двум видам в среднем снизилось на 19 %.
4. Общий индекс цен (по двум методикам):
· общий индекс цен по методике Э. Ласпейреса:
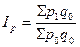
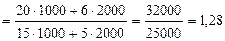 , или 128 %.
, или 128 %.
Таким образом, если бы население приобрело товаров в отчетном периоде столько же, сколько и в базисном, то цены в среднем увеличились бы на 28 %.
· общий индекс цен по методике Г. Пааше: 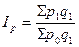
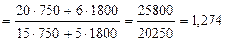 , или 127,4 %.
, или 127,4 %.
Таким образом, средний прирост цен на все товары составил 27,4 %. Заниженное значение индекса цен Г. Пааше объясняется тем, что более резкое повышение цены на товар «А» (на 33,3 %) по сравнению с товаром «Б» (на 20 %) вызвало и более резкое снижение объема покупок (на 25 % по сравнению с 10 %).
5. Общий индекс товарооборота: 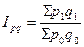
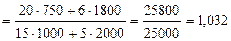 , или 103,2 %.
, или 103,2 %.
Таким образом, товарооборот по двум товарам увеличился на 3,2 %.
6. Абсолютные приросты товарооборота:
· за счет изменения объемов продаж:
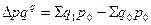
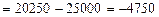 тыс. руб.
тыс. руб.
Таким образом, за счет среднего снижения количества реализованных товаров выручка от продажи снизилась на 4750 тыс. руб.
· за счет изменения цен (по методике Э. Ласпейреса):
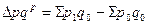
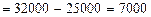 тыс. руб.
тыс. руб.
Таким образом, если бы население в отчетном периоде купило бы столько же товаров, что и в базисном, то в результате среднего роста цен переплата составила бы 7000 тыс. руб.
· за счет изменения цен (по методике Г. Паше):
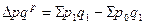
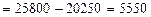 тыс. руб.
тыс. руб.
Таким образом, за счет среднего роста цен денежная выручка продавцов возросла на 555 тыс. руб.; эту же величину составил перерасход денежных средств населения.
· за счет совместного действия обоих факторов:
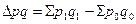
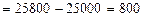 тыс. руб.
тыс. руб.
Таким образом, товарооборот по всем товарам вырос на 800 тыс. руб.
7. Взаимосвязь между индексами: 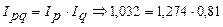
8. Взаимосвязь абсолютных отклонений: 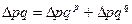
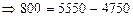 тыс. руб.
тыс. руб.
Индексный метод позволяет не только констатировать изменение среднего уровня, но и определять влияние отдельных факторов на изменение средних показателей. Для этих целей применяют индексы переменного состава, постоянного состава и структурных сдвигов.
Индекс переменного состава представляет собой отношение двух взвешенных средних величин с переменными весами, характеризующее изменение индексируемого (осредняемого) показателя.
Индекс переменного состава для любых качественных показателей имеет следующий вид:
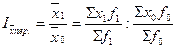 ,
,
где 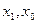 – уровни осредняемого показателя в отчетном и базисном периодах соответственно;
– уровни осредняемого показателя в отчетном и базисном периодах соответственно; 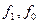 – веса (частоты) осредняемого показателя в отчетном и базисном периодах соответственно. Аналогично строятся индексы средних уровней: цен, себестоимости продукции, фондоотдачи, производительности труда, оплаты труда и т. д.
– веса (частоты) осредняемого показателя в отчетном и базисном периодах соответственно. Аналогично строятся индексы средних уровней: цен, себестоимости продукции, фондоотдачи, производительности труда, оплаты труда и т. д.
Величина этого индекса характеризует изменение средневзвешенной средней за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.
Индекс постоянного (фиксированного) состава представляет собой отношение средних взвешенных с одними и теми же весами (при постоянной структуре). Индекс постоянного состава учитывает изменение только индексируемой величины и показывает средний размер изменения изучаемого показателя ( 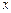 ) у единиц совокупности.
) у единиц совокупности.
В общем виде он может быть записан следующим образом:
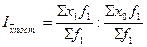 .
.
Индекс структурных сдвигов характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя и определяется по формуле:
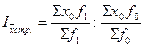
Под структурными изменениями понимается изменении доли отдельных групп единиц совокупности в общей их численности.
Вычисленные по указанным методикам показатели взаимосвязаны, а именно: 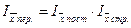 , абсолютные приросты
, абсолютные приросты 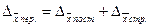
Задача 2.5.2
Имеются следующие данные о производстве продукта «А» по предприятиям:
| Предприятие | Себестоимость, руб. | Выпуск, шт. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| 1 2 | 50 80 | 60 90 | 500 1000 | 1000 1000 |
Определите: индексы себестоимости переменного состава, постоянного состава и структурных сдвигов; абсолютные приросты средней себестоимости по двум факторам вместе и по каждому фактору в отдельности. Покажите взаимосвязь между показателями. Сделайте выводы.
Решение.
1. Индекс себестоимости переменного состава 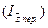 можно записать следующим образом:
можно записать следующим образом:
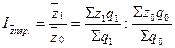 .
.
Тогда,
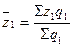
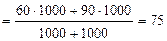 руб.;
руб.;
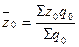
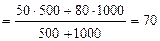 руб.;
руб.;
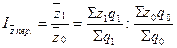
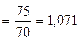 , или 107,1 %.
, или 107,1 %.
При этом абсолютное изменение средней себестоимости 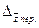 определяется разницей между
определяется разницей между 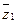 и
и 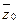 данного индекса:
данного индекса: 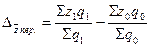
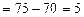 руб.
руб.
2. Индекс себестоимости постоянного состава ( 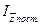 ) имеет следующий вид:
) имеет следующий вид:
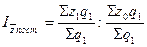
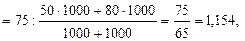 или 115,4 %.
или 115,4 %.
Абсолютное изменение средней себестоимости за счет изменения только себестоимости отдельных видов продукции рассчитываются по формуле:
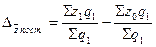
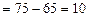 руб.
руб.
3. Индекс себестоимости структурных сдвигов ( 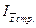 ) имеет следующий вид:
) имеет следующий вид:
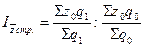
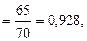 или 92,8 %.
или 92,8 %.
При этом абсолютное изменение средней себестоимости за счет указанного фактора вычисляется по формуле:
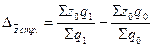
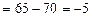 руб.
руб.
Тогда, взаимосвязь:
| между индексами: | 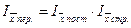 ; ;
|
| 1,071=1,154∙0,928 | |
| 1,071=1,071 | |
| между абсолютными приростами: | 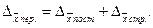 5=10-5
5=5
5=10-5
5=5
|
Таким образом, средняя себестоимость продукта «А» возросла на 7,1 %, или на 5 руб., за счет влияния двух факторов:
а) за счет снижения себестоимости по предприятиям средняя себестоимость возросла на 5,4 %, или на 10 руб.;
б) за счет изменения структуры выпуска продукта (структурного сдвига), т. е. увеличения доли выпуска на предприятии 1 с 33,3 % 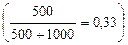 до 50 %
до 50 % 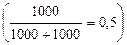 , где себестоимость ниже.
, где себестоимость ниже.
Структурный сдвиг, т. е. увеличение доли выпуска продукта на предприятии с низким уровнем себестоимости (предприятие 1, где себестоимость в базисном периоде составляла 50 руб.) привело к снижению средней себестоимости на 7,2 %, или на 5 руб.
Варианты контрольных заданий
Вариант 1
Задача 1.1
Имеются следующие данные за отчетный год по 30 малым предприятиям одной отрасли экономики, млн. руб.:
| Номер предприятий | Среднегодовая стоимость основных производственных фондов | Выпуск продукции |
| А | 1 | 2 |
| 1 | 49 | 39 |
| 2 | 38 | 35 |
| 3 | 37 | 34 |
| 4 | 56 | 61 |
| 5 | 49 | 50 |
| 6 | 37 | 38 |
| 7 | 33 | 30 |
| 8 | 55 | 51 |
| 9 | 44 | 46 |
| 10 | 41 | 38 |
| 11 | 28 | 35 |
| 12 | 27 | 21 |
| 13 | 46 | 27 |
| 14 | 33 | 41 |
| 15 | 35 | 30 |
| 16 | 41 | 47 |
| 17 | 42 | 42 |
| 18 | 53 | 34 |
| 19 | 55 | 57 |
| 20 | 60 | 46 |
| 21 | 46 | 48 |
| 22 | 39 | 45 |
| 23 | 45 | 43 |
| 24 | 57 | 48 |
| 25 | 56 | 60 |
| 26 | 36 | 35 |
| 27 | 47 | 40 |
| 28 | 20 | 24 |
| 29 | 29 | 36 |
| 30 | 26 | 19 |
1 С целью изучения зависимости между среднегодовой стоимостью основных производственных фондов и выпуском продукции произведите группировку предприятий по среднегодовой стоимости основных производственных фондов, образовав четыре группы предприятий с равными интервалами.
2 По каждой группе и по совокупности предприятий в целом определите:
а) число предприятий;
б) среднегодовую стоимость основных производственных фондов – всего и в среднем на одно предприятие;
в) выпуск продукции – всего и в среднем на одно предприятие;
г) удельный вес предприятий по среднегодовой стоимости основных производственных фондов.
Результаты представьте в табличной форме. Сформулируйте выводы.
Задача 1.2
Имеются следующие данные по предприятию общественного питания за IV квартал, тыс. руб.:
| Показатели | Прогноз | Фактически |
| Товарооборот всего | 2 840 | 2 880 |
| в том числе по собственной продукции | 1 600 | 1 520 |
| Среднесписочная численность работников, чел. | 25 | 23 |
| в том числе поваров, чел. | 11 | 12 |
| Фонд оплаты труда всех работников | 284,0 | 322,6 |
Проанализируйте приведенные данные системой относительных величин. Решение оформите в таблице. Укажите вид используемых величин. Напишите экономические выводы.
Задача 1.3
Имеются следующие данные по трем предприятиям отрасли, выпускающим одинаковую продукцию:
| Номер предприятия | Общие затраты труда на производство продукции, тыс. чел. | Произведено продукции, тыс.шт. |
| 1 | 30 | 5 |
| 2 | 20 | 4 |
| 3 | 80 | 10 |
Рассчитайте среднюю трудоемкость единицы продукции в отрасли и показатели вариации. Объясните экономический смысл полученных результатов.
Задача 1.4
Фонд оплаты труда работников по организации в разрезе месяцев второго полугодия составил:
| Месяц | Июль | Август | Сентябрь | Октябрь | Ноябрь | Декабрь |
| Фонд оплаты труда, тыс. руб. | 110 | 134 | 140 | 156 | 160 | 180 |
На основе показателей динамического ряда сделайте анализ приведенных данных. Укажите вид динамического ряда. Систему расчетов оформите в таблице. Постройте график. Сделайте выводы.
Задача 1.5
Имеются следующие данные о продаже товаров на одном из рынков:
| Вид товаров | Единица измерения | Продано товаров, тыс. ед. | Цена, руб. | ||
| апрель | май | апрель | май | ||
| А | Кг | 68 | 62 | 3,2 | 3,3 |
| Б | Л | 24 | 24 | 4,8 | 5,0 |
| В | Кг | 20 | 16 | 24,0 | 26,4 |
Определите:
а) индивидуальные индексы: объемов продаж в натуральном выражении, цен и товарооборота;
б) общие индексы: физического объема, цен и товарооборота;
в) абсолютные приросты товарооборота за счет изменения: объемов продаж, цен и совместного действия обоих факторов.
Показать взаимосвязь между общими индексами и между абсолютными приростами товарооборота. Сделайте выводы.
Вариант 2
Задача 2.1
Имеются данные о работе 30 предприятий одной из отраслей промышленности за год:
| Номер предприятия | Выпуск продукции, млн. руб. | Среднегодовая стоимость основных производственных фондов, млн. руб. | Численность работающих, чел. |
| А | 1 | 2 | 3 |
| 1 | 65,0 | 54,6 | 340 |
| 2 | 78,0 | 73,6 | 700 |
| 3 | 41,0 | 42,0 | 100 |
| 4 | 54,0 | 46,0 | 280 |
| 5 | 66,0 | 62,0 | 410 |
| 6 | 80,0 | 68,4 | 650 |
| 7 | 45,0 | 36,0 | 170 |
| 8 | 57,0 | 49,6 | 260 |
| 9 | 67,0 | 62,4 | 380 |
| 10 | 81,0 | 71,2 | 680 |
| 11 | 92,0 | 78,8 | 800 |
| 12 | 48,0 | 51,0 | 210 |
| 13 | 59,0 | 60,8 | 230 |
| 14 | 68,0 | 69,0 | 400 |
| 15 | 83,0 | 70,4 | 710 |
| 16 | 52,0 | 50,0 | 340 |
| 17 | 62,0 | 55,0 | 290 |
| 18 | 69,0 | 58,4 | 520 |
| 19 | 85,0 | 83,2 | 720 |
| 20 | 70,0 | 75,2 | 420 |
| 21 | 71,0 | 67,2 | 420 |
| 22 | 64,0 | 64,2 | 400 |
| 23 | 72,0 | 65,0 | 430 |
| 24 | 88,0 | 76,2 | 790 |
| 25 | 73,0 | 68,0 | 560 |
| 26 | 74,0 | 65,6 | 550 |
| 27 | 96,0 | 87,2 | 810 |
| 28 | 75,0 | 71,8 | 570 |
| 29 | 101,0 | 96,0 | 820 |
| 30 | 76,0 | 69,2 | 600 |
По предложенным данным постройте структурную и аналитическую группировки, образовав 5 групп предприятий с равными интервалами. В качестве группировочного признака следует выбрать среднегодовую стоимость основных производственных фондов.
Результаты представьте в табличной форме. Сформулируйте выводы.
Задача 2.2
Имеется информация о поставке мужских ботинок на оптовую базу за отчетный период от двух поставщиков, пар:
| Показатели | Поставщики | |
| ООО «Сапожок» | ООО «Надежда» | |
| Поставлено обуви всего | 10 000 | 17 600 |
| в том числе в соответствии с договором | 9 800 | 15 000 |
| Проверено по качеству всего | 1 000 | 2 640 |
| Из проверенных забраковано и возвращено поставщику | 180 | 550 |
| Общая стоимость поставки, тыс. руб. | 20 000 | 40 480 |
Проанализируйте приведенные данные системой относительных величин. Решение оформите в таблице. Укажите вид используемых относительных величин. Напишите экономические выводы.
Задача 2.3
По данным обследования получены следующие данные о возрастных группах студентов-заочников:
| Номер группы | Возраст, лет. | Число студентов-заочников, чел. |
| 1 | 20-25 | 200 |
| 2 | 25-30 | 900 |
| 3 | 30-35 | 800 |
| 4 | 35-40 | 100 |
| Итого | 2 000 | |
Рассчитайте средний возраст студентов-заочников, среднее линейное отклонение, среднее квадратическое отклонение, коэффициент вариации. Объясните экономический смысл полученных результатов.
Задача 2.4
Отправление грузов железнодорожным транспортом общего пользования за три года характеризуется следующими данными, млн. т.:
| Месяц | 2006г. | 2007г. | 2008г. |
| Январь | 114,0 | 91,5 | 84,1 |
| Февраль | 107,9 | 83,1 | 79,6 |
| Март | 122,6 | 92,8 | 89,1 |
| Апрель | 121,5 | 91,7 | 85,8 |
| Май | 119,6 | 88,7 | 87,6 |
| Июнь | 115,1 | 86,8 | 83,9 |
| Июль | 114,4 | 84,7 | 88,7 |
| Август | 111,2 | 87,9 | 89,0 |
| Сентябрь | 108,1 | 85,3 | 85,9 |
| Октябрь | 110,8 | 89,6 | 88,1 |
| Ноябрь | 100,0 | 85,6 | 82,4 |
| Декабрь | 100,4 | 86,3 | 80,1 |
| Итого | 1345,6 | 1054 | 1024,3 |
Определите индексы сезонности и постройте график сезонной волны.
Задача 2.5
Имеются данные о заработной плате работников по трем районам:
| Район | Среднемесячная заработная плата одного работника, руб. | Среднесписочная численность работников, тыс. чел. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| 1 2 3 | 670 750 820 | 700 800 900 | 6,0 4,0 10,0 | 5,0 4,5 12,0 |
Определить изменение общего фонда оплаты труда по трем районам под влиянием двух факторов – изменения общей численности работающих и заработной платы и каждого из этих факторов в отдельности.
Вариант 3
Задача 3.1
Имеются данные за отчетный период по 30 предприятиям торговли региона:
| Номер предприятий | Средняя заработная плата, тыс. руб. | Выработка продавцов, тыс. руб. |
| А | 1 | 2 |
| 1 | 31 | 160 |
| 2 | 37 | 97 |
| 3 | 38 | 105 |
| 4 | 48 | 170 |
| 5 | 55 | 183 |
| 6 | 56 | 149 |
| 7 | 65 | 205 |
| 8 | 75 | 315 |
| 9 | 15 | 52 |
| 10 | 29 | 95 |
| 11 | 42 | 126 |
| 12 | 41 | 150 |
| 13 | 43 | 140 |
| 14 | 59 | 177 |
| 15 | 58 | 240 |
| 16 | 49 | 191 |
| 17 | 70 | 270 |
| 18 | 67 | 207 |
| 19 | 52 | 190 |
| 20 | 57 | 145 |
| 21 | 28 | 102 |
| 22 | 36 | 180 |
| 23 | 36 | 122 |
| 24 | 57 | 240 |
| 25 | 51 | 140 |
| 26 | 63 | 140 |
| 27 | 62 | 183 |
| 28 | 52 | 155 |
| 29 | 20 | 86 |
| 30 | 18 | 90 |
1 С целью изучения зависимости между заработной платой и выработкой продавцов торговых предприятий региона произведите группировку предприятий торговли по заработной плате, образовав четыре группы предприятий торговли с равными интервалами.
2 По каждой группе и по совокупности предприятий торговли в целом определите:
а) число предприятий торговли;
б) сумму заработной платы – всего и в среднем на одно предприятие торговли;
в) сумму выработки продавцов – всего и в среднем на одно предприятие торговли;
г) удельный вес заработной платы.
Результаты представьте в табличной форме. Сформулируйте выводы.
Задача 3.2
Имеются следующие данные по торговому предприятию «Тереза» за два полугодия:
| Показатели | Полугодие | |
| первое | второе | |
| Товарооборот, тыс. руб. | 1 550 | 1658 |
| в том числе по импортным товарам, тыс. руб. | 1 043 | 1 070 |
| Среднесписочная численность работников, чел. | 9 | 10 |
| Фонд оплаты труда, тыс. руб. | 275,9 | 331,6 |
Проанализируйте приведенные данные системой относительных величин. Решение оформите в таблице. Укажите вид используемых относительных величин. Напишите экономические выводы.
Задача 3.3
Имеются следующие данные о стаже работы служащих двух филиалов банка на 1 января 2009г.:
| Филиал 1 | Филиал 2 | ||
| Стаж работы, лет | Число служащих, чел. | Стаж работы, лет | Число служащих, чел. |
| 1-3 | 2 | 1-3 | 3 |
| 3-6 | 5 | 3-6 | 5 |
| 6-10 | 6 | 6-10 | 7 |
| 10-15 | 3 | 10-15 | 4 |
| 15-20 | 2 | 15-20 | 1 |
Рассчитайте в каждом филиале средний стаж работы служащих и показатели вариации. Решение оформите в таблице. Объясните экономический смысл полученных результатов.
Задача 3.4
Производство электроэнергии в регионе в 2001-2008гг. характеризуется следующими данными, млрд. кВт∙ч:
| 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 |
| 915 | 976 | 1038 | 1111 | 1150 | 1202 | 1239 | 1294 |
Определить аналитические показатели ряда динамики производства электроэнергии за 2001-2008гг.: абсолютные приросты; темпы роста и темпы прироста; абсолютное значение одного процента прироста; средние обобщающие показатели ряда динамики.
Систему расчетов оформите в таблице. Постройте график. Сделайте выводы.
Задача 3.5
Имеются следующие данные о реализации мясных продуктов на городском рынке:
| Продукт | Сентябрь | Октябрь | ||
| цена за 1 кг, руб. | продано, ц. | цена за 1 кг, руб. | продано, ц. | |
| Говядина Баранина Свинина | 70 60 90 | 26,3 8,8 14,5 | 80 60 95 | 24,1 9,2 12,3 |
Рассчитайте сводные индексы цен, физического объема реализации и товарооборота, а также величину перерасхода покупателей от роста цен.
Вариант 4
Задача 4.1
Имеются данные о работе 25 предприятий одной из отраслей промышленности за год:
| Номер предприятия | Выпуск продукции, млн. руб. | Численность работающих, чел. | Прибыль, млн. руб. |
| А | 1 | 2 | 3 |
| 1 | 65,0 | 340 | 15,7 |
| 2 | 78,0 | 700 | 18,0 |
| 3 | 41,0 | 100 | 12,1 |
| 4 | 54,0 | 280 | 13,8 |
| 5 | 66,0 | 410 | 15,5 |
| 6 | 80,0 | 650 | 17,9 |
| 7 | 45,0 | 170 | 12,8 |
| 8 | 57,0 | 260 | 14,2 |
| 9 | 67,0 | 380 | 15,9 |
| 10 | 81,0 | 680 | 17,6 |
| 11 | 92,0 | 800 | 18,2 |
| 12 | 48,0 | 210 | 13,0 |
| 13 | 59,0 | 230 | 16,5 |
| 14 | 68,0 | 400 | 16,2 |
| 15 | 83,0 | 710 | 16,7 |
| 16 | 52,0 | 340 | 14,6 |
| 17 | 62,0 | 290 | 14,8 |
| 18 | 69,0 | 520 | 16,1 |
| 19 | 85,0 | 720 | 16,7 |
| 20 | 70,0 | 420 | 15,8 |
| 21 | 71,0 | 420 | 16,4 |
| 22 | 64,0 | 400 | 15,0 |
| 23 | 72,0 | 430 | 16,5 |
| 24 | 88,0 | 790 | 18,5 |
| 25 | 73,0 | 560 | 16,4 |
По предложенным данным постройте структурную и аналитическую группировки, образовав 6 групп предприятий с равными интервалами. В качестве группировочного признака следует выбрать численность работающих. Результаты представьте в табличной форме. Сформулируйте выводы.
Задача 4.2
Имеются следующие данные по кафе «Быстро» за два квартала, тыс. руб.
| Показатели | I квартал | V квартал |
| Выпуск блюд, тыс. шт. | 570 | 599 |
| в том числе кондитерские, тыс. шт. | 200 | 350 |
| Товарооборот | 1 440 | 1 478 |
| Стоимость основных фондов | 1 080 | 1 240 |
| в том числе оборудования | 466 | 690 |
Проанализируйте приведенные данные системой относительных величин. Решение оформите в таблице. Укажите вид используемых относительных величин. Напишите экономические выводы.
Задача 4.3
Для определения наиболее предпочтительного варианта инвестиций в течение 5 периодов проводилось наблюдение за результатами работы трех предприятий. Получены следующие данные о прибыли этих предприятий, млн. руб.:
| Предприятие | Период | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 80 | 75 | 60 | 70 | 65 |
| 2 | 140 | 120 | 60 | 60 | 120 |
| 3 | 90 | 60 | 80 | 50 | 70 |
Определите с помощью коэффициента вариации предприятие, у которого показатель прибыли наиболее стабилен.
Задача 4.4
Имеются следующие данные о внутригодовой динамике ввода в действие жилых домов предприятиями всех форм собственности в одном из регионов по кварталам, млн. кв. м. общей жилой площади:
| Квартал | 2005 г. | 2006 г. | 2007 г. | 2008 г. |
| I | 2,2 | 2,4 | 2,1 | 2,0 |
| II | 5,1 | 5,0 | 4,2 | 5,7 |
| III | 3,9 | 4,8 | 4,1 | 6,0 |
| IV | 8,4 | 9,0 | 6,4 | 15,0 |
Выявите основную тенденцию данных о внутригодовой динамике ввода в действие жилых домов предприятиями всех форм собственности в одном из регионов по кварталам 2005-2008 гг.:
а) методом скользящей средней;
б) методом аналитического выравнивания.
Сделайте соответствующие выводы.
Задача 4.5
Имеются следующие данные о реализации продовольственных товаров по магазинам города за два квартала:
| Товары | III квартал | IV квартал | ||
| количество, ц. | цена за 1 кг, руб. | количество, ц. | цена за 1 кг, руб. | |
| Сахар Мука Масло | 997 650 342 | 13,3 12,0 45,5 | 1230 680 335 | 14,0 12,5 55,5 |
Проанализируйте динамику розничного товарооборота, используя индексный метод. Решение оформите в таблице. Напишите выводы.
Вариант 5
Задача 5.1
За отчетный период по предприятиям торговли района имеются данные о реализации товаров и издержках обращения, тыс. руб.:
| Номер предприятий | Розничный товарооборот | Издержки обращения |
| А | 1 | 2 |
| 1 | 511 | 30,0 |
| 2 | 560 | 34,0 |
| 3 | 800 | 46,0 |
| 4 | 465 | 30,9 |
| 5 | 228 | 15,9 |
| 6 | 392 | 25,2 |
| 7 | 640 | 42,0 |
| 8 | 404 | 27,0 |
| 9 | 200 | 16,4 |
| 10 | 425 | 34,8 |
| 11 | 570 | 37,0 |
| 12 | 472 | 28,6 |
| 13 | 250 | 18,7 |
| 14 | 665 | 39,0 |
| 15 | 650 | 36,0 |
| 16 | 620 | 36,0 |
| 17 | 383 | 25,0 |
| 18 | 550 | 38,5 |
| 19 | 750 | 44,0 |
| 20 | 660 | 37,0 |
| 21 | 452 | 27,0 |
| 22 | 563 | 35,0 |
1 Для выявления зависимости между объемом розничного товарооборота и издержками обращения сгруппируйте предприятия торговли по объему розничного товарооборота, образовав пять групп с равными интервалами.
2 По каждой группе предприятий торговли и их совокупности определите:
а) число предприятий;
б) объем розничного товарооборота – всего и в среднем на одно предприятие;
в) сумму издержек обращения – всего и в среднем на одно предприятие;
г) удельный вес издержек обращения.
Результаты представьте в табличной форме. Сформулируйте выводы.
Задача 5.2
Имеются следующие данные о деятельности двух предприятий общественного питания за 2008г.:
| Показатели | ООО «Вкусняшка» | ООО «Петушок» |
| Товарооборот, тыс. руб. | 2 422 | 2 667 |
| Число посадочных мест, шт. | 30 | 45 |
| Среднесписочное число посетителей, чел. | 180 | 240 |
| Вся площадь, кв.м. | 200 | 250 |
| в том числе обеденный зал, кв.м. | 90 | 100 |
Проанализируйте приведенные данные системой относительных величин. Решение оформите в таблице. Укажите вид используемых относительных величин. Напишите экономические выводы.
Задача 5.3
Имеются данные о группировке магазинов по величине доходов от торговой деятельности по торговой фирме за отчетный период:
| Доход на одно предприятие, тыс. руб. | Число магазинов |
| 50-60 | 2 |
| 60-70 | 3 |
| 70-80 | 1 |
| 80-90 | 4 |
| 90-100 | 5 |
Рассчитайте все показатели вариации. Решение оформите в таблице. Объясните экономический смысл полученных результатов. Проанализируйте динамику вариации, если известно, что коэффициент вариации за прошлый период 30 %.
Задача 5.4
Сумма товарных запасов на начало года по торговой организации «Тигр» составила, тыс. руб.
| Годы | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 |
| Товарные запасы | 220 | 244 | 268 | 379 | 490 | 510 |
Проанализируйте данный динамический ряд системой показателей, найденных базисным и цепным способами. Найдите средние значения для этого ряда. Необходимые расчеты выполните в таблице. Укажите вид динамического ряда. Сделайте выводы по результатам расчетов.
Задача 5.5
Имеются данные о заработной плате работников по двум группам населения:
| Группа населения | Среднемесячная заработная плата (одного работника), руб. | Среднесписочная численность работников, тыс. руб. | ||
| 2000г. | 2001г. | 2000г. | 2001г. | |
| Сельское Городское | 7200 10800 | 9000 12600 | 900 4200 | 1000 4300 |
Определить по двум группам населения индексы средней заработной платы: переменного состава, постоянного состава и структурных сдвигов. Сделайте соответствующие выводы.
Дата: 2018-12-28, просмотров: 486.