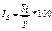Процесс развития в статистике называется динамикой, а система показателей, характеризующих этот процесс во времени, – рядом динамики (хронологическим рядом).
В любом ряде динамики выделяют два основных элемента: показатель времени, уровень ряда.
Если показатель времени представлен моментом (характеризует состояние явления на определенную дату), то такой ряд динамики называется моментным. Если показатель времени представлен временным интервалом (характеризует результат развития за определенный период), то такой динамический ряд называется интервальным.
В зависимости от вида ряда динамики некоторые показатели его анализа определяются по-разному.
Общепринятые обозначения уровней рядов динамики следующие: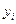 
– данный уровень, 
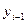– предыдущий уровень, 
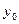– базисный уровень, 
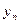– конечный уровень, 
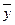– средний уровень.
Средний уровень интервального ряда динамики в случае равенства этих интервалов определяется по формуле средней арифметической простой: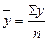 
.
Если интервальный ряд динамики имеет неравностоящие уровни, то средний уровень ряда вычисляется по формуле:
,
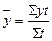где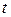 
– число периодов времени, в течение которых уровень не изменяется.
Средний уровень для моментного ряда в случае, если временные расстояния между этими моментами (датами) одинаковы, определяется по формуле средней хронологической:
,
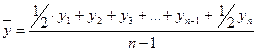где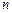 
– число уровней ряда.
Средняя хронологическая для разностоящих уровней моментного ряда динамики вычисляется по формуле:
.
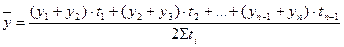Графически ряды динамики изображаются в основном либо линейными, либо столбиковыми диаграммами. Но в любом случае по оси абсцисс откладываются показатели времени, а по оси ординат – уровни ряда.
Аналитические показатели рядов динамики строятся на основе сравнения (сопоставления) двух уровней ряда. В каждом ряде динамики, представленном не двумя, а большим числом уровней, сопоставление возможно между смежными уровнями (данным уровнем с предыдущем), образующими систему цепных показателей, и между данным уровнем и уровнем, принятым за базу сравнения. Последнее создает систему базисных показателей анализа рядов динамики. Исчисляют следующие основные аналитические показатели рядов динамики: абсолютный прирост, темп роста, темп прироста, абсолютное значение (содержание) одного процента прироста.
Абсолютный прирост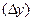 
определяется как разность между двумя уровнями динамического ряда. Показывает, на сколько в абсолютном выражении уровень текущего периода больше (меньше) базисного. Различают:
· цепной абсолютный прирост: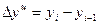 
;
· базисный абсолютный прирост: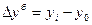 
.
Цепные и базисные абсолютные приросты взаимосвязаны:
· сумма цепных абсолютных приростов равна конечному базисному абсолютному приросту;
· разность между двумя смежными базисными приростами равна промежуточному цепному.
Обобщением цепных абсолютных приростов за период является средний абсолютный прирост: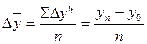 
,
где 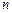– число цепных абсолютных приростов, 
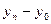– конечный базисный абсолютный прирост.
Темп роста (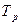 
) – отношение уровней ряда динамики, которое выражается в коэффициентах или процентах. Показывает, во сколько раз увеличился уровень динамического ряда по сравнению с базисным, а в случае уменьшения – какую часть базисного составляет сравниваемый уровень. Различают:
· цепной темп роста: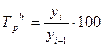 
;
· базисный темп роста: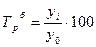 
.
Между цепными и базисными темпами роста существует взаимосвязь:
· произведение цепных темпов роста равно конечному базисному;
· частное от деления двух смежных базисных темпов роста равно промежуточному цепному.
Обобщением цепных темпов роста за период является средний темп роста, который определяется по формулам:
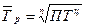, или 
,
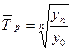где 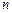– число цепных абсолютных приростов, 
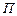– знак произведения.
Темп прироста (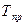 
) показывает, на сколько процентов уровень данного периода больше (или меньше) базисного уровня. Этот показатель может быть рассчитан двумя способами:
а) как отношение абсолютного прироста к уровню, принятому за базу сравнения:
· цепной темп прироста: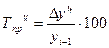 
;
· базисный темп прироста: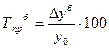 
.
б) как разность между темпами роста и единицей, если темпы роста выражены в коэффициентах; или как разность между темпами роста и 100 %, если темпы роста выражены в процентах:
· цепной темп прироста: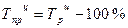 
;
· базисный темп прироста: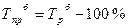 
.
Средний темп прироста определяется следующим образом: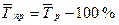 
.
Абсолютное значение одного процента прироста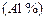 
– отношение абсолютного прироста на соответствующий темп прироста и показывает, как в абсолютном выражении изменяется явление при его росте (снижении) на 1 %. Различают:
· цепным способом: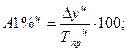 
· базисным способом: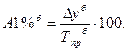 
Расчет среднего абсолютного значения одного процента прироста производится по формуле: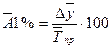 
.
Примечание: при оформлении контрольной работы соответствующие расчеты по индивидуальным показателям (базисным и цепным методом) следует не рассчитывать подробно, а сразу показывать в таблице.
Задача 2.4.1
Имеются следующие данные о продаже товаров в торговой организации «Изобилие» по месяцам второго полугодия:
| Месяцы | июль | август | сентябрь | октябрь | ноябрь | декабрь |
| Стоимость, тыс. руб. | 1260 | 1450 | 1570 | 1660 | 1810 | 1960 |
Проанализируйте динамический ряд по системе показателей. Индивидуальные показатели рассчитайте базисным и цепным методом. Решение оформите в таблице. Рассчитайте средние характеристики. Постойте график. Напишите экономические выводы.
Решение.
1. Расчет индивидуальных показателей ряда динамики:
1.1 Абсолютный прирост:
· базисные абсолютные приросты:
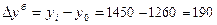тыс. руб.;
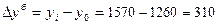тыс. руб.;
и т. д. таблица 4.1 графа 2.
· цепные абсолютные приросты:
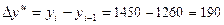тыс. руб.;
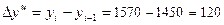тыс. руб.;
и т. д. таблица 4.1 графа 3.
1.2 Темп роста:
· базисный темп роста:
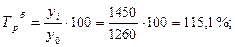
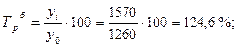
и т. д. таблица 4.1 графа 4.
· цепной темп роста:
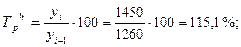
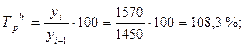
и т. д. таблица 4.1 графа 5.
1.3 Темп прироста:
· базисный темп прироста:
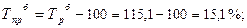
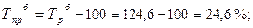
и т. д. таблица 4.1 графа 6.
· цепной темп прироста:
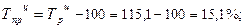
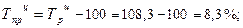
и т. д. таблица 4.1 графа 7.
1.4 Абсолютное значение одного процента прироста:
· базисным способом:
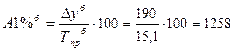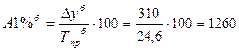руб.;
руб.;
и т. д. таблица 4.1 графа 8.
· цепным способом:
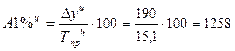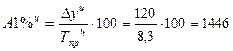руб.;
руб.;
и т. д. таблица 4.1 графа 9.
2. Расчет средних показателей:
2.1 В данном случае ряд – интервальный, интервалы равны, используем формулу средней арифметической простой:
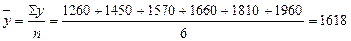тыс. руб.
Таким образом, среднемесячная продажа за второе полугодие в организации «Изобилие» достигла размера 1618 тыс. руб.
Таблица 4.1 – Исходные и расчетные данные для анализа динамики продажи товаров в торговой организации «Изобилие» по месяцам второго полугодия
| Месяцы | Стоимость, тыс. руб. | Абсолютный прирост, тыс. руб. | Темпы роста, % | Темпы прироста, % | Абсолютное значение 1 % прироста, руб. | ||||
| базисные | цепные | базисные | цепные | базисные | цепные | базисные | цепные | ||
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Июль Август Сентябрь Октябрь Ноябрь Декабрь | 1260 1450 1570 1660 1810 1960 | Х 190 310 400 550 700 | Х 190 120 90 150 150 | Х 115,1 124,6 131,8 143,7 155,6 | Х 115,1 108,3 105,7 109,0 108,3 | Х 15,1 24,6 31,8 43,7 55,6 | Х 15,1 8,3 5,7 9,0 8,3 | Х 1258 1260 1258 1259 1259 | Х 1258 1446 1579 1667 1807 |
2.2 Средний абсолютный прирост:
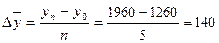тыс. руб., (или по формуле: 
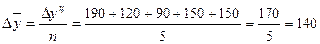тыс. руб.).
Таким образом, в анализируемом периоде происходило наращивание продажи при переходе от одного месяца к другому в денежном выражении в среднем на сумму 140 тыс. руб.
2.3 Среднемесячный темп роста: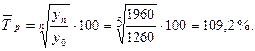 
Таким образом, во втором полугодии средний темп роста реализации товаров в торговой организации «Изобилие» составил 109,2 %.
2.4 Средний темп прироста: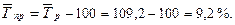 
Таким образом, в данном периоде происходило наращивание торговой выручки при переходе от одного месяца к другому в относительной форме в среднем на 9,2 %.
2.5 Среднее значение одного процента прироста:
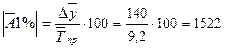руб.
Таким образом, во втором полугодии в торговой организации «Изобилие» рост выручки на 1 % сопровождался дополнительной продажей товаров населению в среднем на сумму 1522 руб.
Построим графическое изображение по графам 4 и 5 таблицы 4.1.
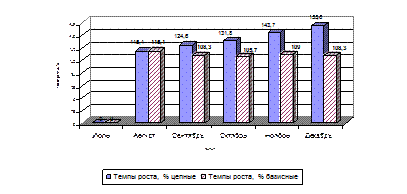
Рисунок 4.1 – Динамика продажи товаров в торговой
организации «Изобилие» по месяцам второго полугодия, %
Таким образом, среднемесячный объем реализации товаров в торговой организации «Изобилие» в данном периоде достиг уровня 162 тыс. руб., от месяца к месяцу товарооборот прирастал в среднем на сумму 14 тыс. руб., или на 9,2 %. Рост выручки на 1 % обеспечил торговой организации дополнительный объем продажи в денежном выражении на 1522 руб.
В целом за изучаемый период продажа товаров выросла с 1260 до 1960 тыс. руб., т. е. на 700 тыс. руб., или почти на 56 %. 1 % увеличения этого показателя соответствовал в среднем 1258 – 1260 руб. дополнительной продажи. Данные таблицы 4.1 графы 2, 4, 6 и рисунок 4.1 свидетельствуют об устойчивой положительной динамике анализируемого показателя за изучаемый период данное обстоятельство позитивно отражается на других экономических показателях торговой организации «Изобилие» (например, доходы, заработная плата, при оптимальных затратах – прибыли, рентабельность).
При помесячном сравнении объема продажи динамика получается несколько иной. В данном случае можно проследить отдельные этапы изменения анализируемого показателя, а именно:
а) период роста: январь–февраль с увеличением продажи на 190 тыс. руб. при темпе роста 115,1 %; апрель–май соответственно на 150 тыс. руб. и 109,0 %;
б) период снижения: февраль–апрель, помесячные темпы прироста составляли 8,3 и 5,7 %, а абсолютные приросты 120 и 90 тыс. руб. соответственно;
в) период относительной стабилизации: май–июнь – одинаковое наращивание показателя в абсолютном выражении – на 150 тыс. руб. и в относительной форме – примерно на 9 %.
Проведенное динамическое исследование продажи товаров в торговой организации «Изобилие» по месяцам второго полугодия позволяет констатировать следующее: объем реализации товаров растет, и это положительно характеризует работу торговой организации «Изобилие» в плане постановки коммерческой и экономической деятельности; внутри полугодия под влиянием различных факторов отмечались периоды роста и спада торговой выручки; при благоприятном стечении обстоятельств и грамотном ведении торгового процесса можно ожидать дальнейший рост анализируемого показателя.
Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития.
При изучении в рядах динамики основной тенденции развития явления применяются: метод укрупнения интервалов, метод ступенчатой средней, метод скользящей средней, аналитическое выравнивание. Каждый из этих методов имеет свои достоинства и недостатки и может быть использован в зависимости от особенностей исходных данных и целей исследования.
Укрупнение периодов – это метод выравнивания, при котором исходный ряд динамики преобразуется в новый ряд путем укрупнения продолжительности периодов.
Метод ступенчатой средней заключается в том, что для укрупненных периодов рассчитывается средний уровень.
Метод скользящей средней. Суть метода состоит в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т. е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего. Нахождение скользящей средней по четному числу членов осложняется тем, что средняя может быть отнесена только к середине между двумя датами. Чтобы ликвидировать этот сдвиг, применяется центрирование, т. е. нахождение средней из средних для отнесения полученного уровня к определенной дате. При центрировании необходимо также находить скользящие суммы, скользящие средние по этим суммам и средние из средних.
Аналитическое выравнивание – это замена эмпирического ряда динамики теоретическими значениями, представленными как функция от времени: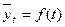 
.
Аналитическое выравнивание может быть осуществлено по любому рациональному многочлену. Выбор функции производится на основе анализа характера закономерностей динамики данного явления.
Линейная функция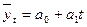 
, (где 
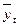– теоретические уровни, 
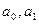– параметры прямой, 
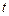– показатель времени (дни, месяцы, годы и т. д.)) используется, когда первые разности уровней ряда (абсолютные приросты) относительно постоянны. Для линейной функции параметр 
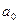можно интерпретировать как значение начального уровня ряда динамики, а параметр 
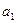– как средний абсолютный прирост за рассматриваемый период. Для нахождения параметров 
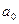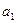и необходимо решить систему нормальных уравнений: 
,
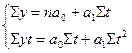где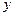 
– фактические уровни ряда динамики, 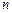– число уровней. Параболы второго порядка 
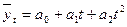используются для отражения ряда динамики с постоянными вторыми разностями (ускорениями). При относительно постоянных коэффициентах роста выравнивание динамического ряда производится по показательной экспонентной кривой: 
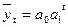. В этом случае параметр 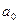является средней геометрической эмпирического ряда динамики, а параметр 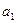– средним коэффициентом роста ряда.
Задача 2.4.2
Известны следующие данные о выпуске продукции «А» за месяц, тыс. шт.:
| 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 |
| 10,0 | 10,7 | 12,0 | 10,3 | 12,9 | 16,3 | 15,6 | 17,8 | 18,0 |
Выявить основную тенденцию выпуска продукции «А» за 2000 – 2008 гг.: методом скользящей средней и методом аналитического выравнивания.
Решение.
1. Выявим основную тенденцию выпуска продукции «А» за 2000–2008 гг. методом скользящей средней, для этого исчислим трехлетние скользящие средние уровни ряда:
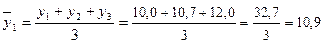тыс. шт.
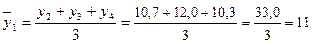тыс. шт. и т. д.
Результаты расчета трехлетней скользящей средней представим в таблице 4.2.
Таблица 4.2 – Динамика выпуска продукции «А» за месяц за 2000–2008 гг., тыс. шт.
| Год | Выпуск продукции «А» за месяц
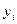
| Скользящие трехлетние суммы
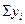
| Трехлетние скользящие средние
|
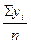
| 2000 2001 2002 2003 2004 2005 2006 2007 2008 | 10,0 10,7 12,0 10,3 12,9 16,3 15,6 17,8 18,0 | - 32,7 33,0 35,2 39,5 44,8 49,7 51,4 - | - 10,9 11,0 11,8 13,2 15,9 16,6 17,1 - |
Таким образом, скользящие средние, освобожденные от случайных колебаний, неуклонно возрастают, характеризуя явную тенденцию к росту выпуска продукции «А» за 2000–2008 гг.
2. Выявим основную тенденцию выпуска продукции «А» за 2000–2008 гг. методом аналитического выравнивания ряда динамики по прямой: .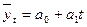
Для нахождения параметров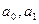 
решим систему нормальных уравнений: 
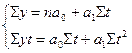. Для упрощения расчетов обозначим время так, чтобы начало его отсчета приходилось на середину рассматриваемого периода таблица 4.3 графа 2.
Таблица 4.3 – Расчетные данные для определения параметров системы нормальных уравнений и выровненных теоретических значений
| Год | Выпуск продукции «А» за месяц
 
| 
| 
| 
|
|
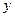
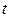
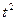
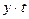
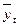
| А | 1 | 2 | 3 | 4 | 5 |
| 2000 2001 2002 2003 2004 2005 2006 2007 2008 | 10,0 10,7 12,0 10,3 12,9 16,3 15,6 17,8 18,0 | -4 -3 -2 -1 0 1 2 3 4 | 16 9 4 1 0 1 4 9 16 | -40,0 -32,1 -24,0 -10,3 0 16,3 31,2 53,4 72,0 | 9,30 10,41 11,52 12,63 13,74 14,85 15,96 17,07 18,18 |
| Итого | 123,6 | 0 | 60 | 66,5 | 123,66 |
Так как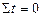 
, то система нормальных уравнений примет вид: 
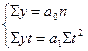. Тогда, 
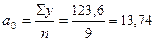тыс. шт., 
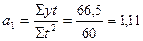тыс. шт.
Уравнение прямой будет иметь вид: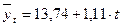 
. Подставив в это уравнение значение 
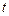таблица 4.3, графа 2, получим выровненные значения 
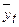выпуска продукции таблица 4.3, графа 5. При этом 
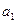=1,11 означает, что год от года выпуск продукции «А» в среднем возрастает на 1,11 тыс. шт. Это выровненная, устойчивая, неуклонно возрастающая от года к году тенденция.
При анализе рядов динамики важное значение имеет выявление сезонных колебаний. Этим колебаниям свойственны более или менее устойчивые изменения уровней ряда по внутригодовым периодам: месяцам, кварталам. Для выявления сезонных колебаний обычно анализируются месячные и квартальные уровни ряда динамики за год или за несколько лет.
При изучении сезонных колебаний используются специальные показатели – индексы сезонности (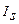 
). Для исчисления индексов сезонности применяют различные методы, выбор которых зависит от характера общей тенденции ряда динамики.
Если ряд динамики не содержит ярко выраженной тенденции развития, то индексы сезонности исчисляют непосредственно по эмпирическим данным без их предварительного выравнивания. Для расчета индексов сезонности необходимо иметь помесячные данные как минимум за три года.
Для каждого месяца рассчитывается средний уровень (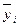 
), затем исчисляется среднемесячный уровень для всего анализируемого ряда ( 
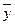). По этим данным определяется индекс сезонности ( 
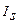) как процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда:
,
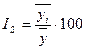где 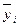– среднемесячные уровни ряда (по одноименным месяцам); 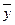– общий средний уровень ряда (постоянная средняя).
Если уровни ряда динамики проявляют тенденцию к росту или снижению, то отклонения от постоянного среднего уровня могут исказить сезонные колебания. В таких случаях фактические данные сопоставляются с выровненными.
Для расчета индекса сезонности в таких рядах динамики применяется формула:
,
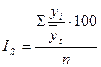где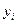 
– эмпирические уровни ряда; 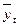– теоретические уровни ряда; 
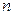– число лет.
Задача 2.4.3
Реализация товара на рынках города за 2006–2008 гг. характеризуется следующими данными, т.:
| Годы | Месяцы | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| 2006 2007 2008 | 70 71 63 | 71 85 60 | 82 84 59 | 190 308 261 | 280 383 348 | 472 443 483 | 295 261 305 | 108 84 129 | 605 630 670 | 610 450 515 | 184 177 185 | 103 168 104 |
Определить индексы сезонности.
Решение.
Применяя формулу средней арифметической простой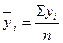 
, определим среднемесячные уровни за три года:
Январь: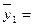 
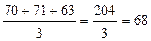т.
Февраль: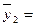 
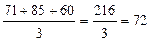т.
и т. д. таблица 4.4, графа 5.
Исчислим общую (постоянную) среднюю (итог графы 5, таблицы 4.4):
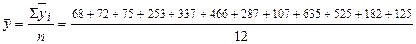= 261 т., или 
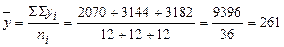т.
Таблица 4.4 – Реализация товара на рынках города за три года
|
Месяц | Реализация товара | Индексы сезонности, %
| ||||
| 2006 | 2007 | 2008 | Сумма за три года | Среднемесячная за три года
| ||
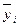
| А | 1 | 2 | 3 | 4 | 5 | 6 |
| Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь | 70 71 82 190 280 472 295 108 605 610 184 103 | 71 85 84 308 383 443 261 84 630 450 177 168 | 63 60 59 261 348 483 305 129 670 515 185 104 | 204 216 225 759 1011 1398 861 321 1905 1575 546 375 | 68 72 75 253 337 466 287 107 635 525 182 125 | 26,3 27,6 28,7 96,9 129,1 178,5 110,0 41,0 243,3 201,0 69,7 47,9 |
| Итого | 3070 | 3144 | 3182 | 9396 | 261 | 100,0 |
Индексы сезонности имеют следующие значения таблица 4.4, графа 6:
Январь: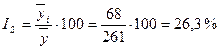 
;
Февраль: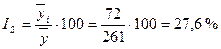 
и т. д.
Для наглядности построим график сезонной волны реализации товара рисунок 4.2.
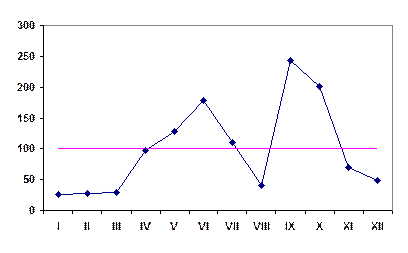
Рисунок 4.2 – Сезонная волна реализации товара
(изменение индексов сезонности в среднем за три года)
Таким образом, индексы сезонности показывают, что наименьший спрос товара на рынках города за 2006–2008 гг. приходится на январь–февраль, а наибольший – на сентябрь–октябрь.
Дата: 2018-12-28, просмотров: 267.
