Наиболее распространенной формой статистических показателей, используемой в социально-экономических исследованиях, является средняя величина.
Средняя величина – это обобщенная характеристика признака в статистической совокупности, она выражает характерную, типичную величину признака у единиц совокупности, образующихся в конкретных условиях места и времени под влиянием различных факторов.
Основные виды средних, чаще всего применяемых в практике статистических расчетов, следующие:
| Наименование | Простая форма | Взвешенная форма |
Средняя арифметическая ( 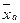 ) )
| 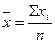
| 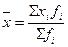
|
Средняя квадратическая ( 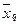 ) )
| 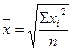
| 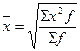
|
Средняя гармоническая ( 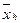 ) )
| 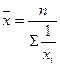
| 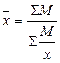
|
Средняя геометрическая ( 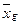 ) )
|  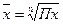
| 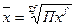
|
Где 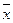 – среднее значение признака;
– среднее значение признака; 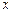 – значения признака;
– значения признака; 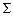 – знак суммирования;
– знак суммирования; 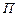 – знак перемножения;
– знак перемножения; 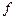 (частота) и
(частота) и 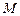 (произведение частоты на значения признака) – веса для расчета взвешенной средней;
(произведение частоты на значения признака) – веса для расчета взвешенной средней; 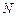 и
и 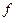 – численность единиц совокупности;
– численность единиц совокупности; 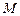 – общий объем варьирующего признака.
– общий объем варьирующего признака.
Если средние вычислить по одним и тем же данным, то приведенные виды средних по своим численным значениям встают в следующий ряд: 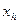 <
< 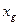 <
< 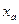 <
< 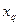 , иллюстрируя так называемое правило мажорантности средних.
, иллюстрируя так называемое правило мажорантности средних.
Одна из задач определения средней состоит в правильности выбора вида средней величины. При выборе вида средней необходимо учитывать экономическое содержание индивидуальных признаков, которое должно быть сохранено и в итоговой средней величине. При этом любые промежуточные действия, включая конечный результат, должны быть экономически значимы.
Наибольшее распространение получила средняя арифметическая, как простая, так и взвешенная. Средняя арифметическая простая применяется в случаях, когда варианты представлены в виде их перечня в любом порядке или ранжированного ряда. Если данные представлены в виде дискретных или интервальных рядов распределения, в которых одинаковые значения признака объединены в группы, имеющие различное число единиц, называемое частотой (весом), применяется средняя арифметическая взвешенная.
Наряду с расчетом средней для вариационных рядов распределения исчисляют структурные средние – моду, медиану.
Мода – это значение признака (варианта), которое чаще всего встречается в исследуемой совокупности и имеет наибольшую частоту.
Медианой называется значение признака (варианта), которое находится в середине вариационного ряда и делит его пополам.
В интервальном вариационном ряду мода рассчитывается по формуле:
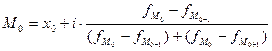 ,
,
где 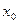 – минимальная граница модального интервала,
– минимальная граница модального интервала, 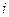 – величина модального интервала,
– величина модального интервала, 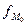 – частота модально интервала,
– частота модально интервала, 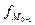 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному; 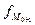 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
Медиана для интервального ряда распределения рассчитывается по формуле:
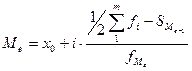 ,
,
где 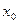 – нижняя граница медианного интервала,
– нижняя граница медианного интервала, 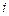 – величина медианного интервала,
– величина медианного интервала, 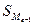 – сумма накопленных частот, предшествующих медианному,
– сумма накопленных частот, предшествующих медианному, 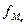 – частота медианного интервала.
– частота медианного интервала.
При изучении совокупности явления нельзя ограничиваться нахождением средней величины. Необходимо исследовать разброс, различия индивидуальных значений признака, причины, вызывающие эти различия. Различие значений признака у разных единиц совокупности называется вариацией. Для измерения и оценки вариации используют абсолютные и относительные показатели. К абсолютным показателям относят: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Размах вариации ( 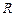 ) – абсолютная разность между максимальным и минимальным значениями признака в изучаемой совокупности:
) – абсолютная разность между максимальным и минимальным значениями признака в изучаемой совокупности:
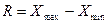 .
.
Среднее линейное отклонение ( 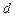 ) – показывает средний разброс индивидуальных значений от среднего показателя без учета направленности по модулю. Его можно рассчитать как по формуле средней арифметической простой, так и по формуле средней арифметической взвешенной, в зависимоти от отсутствия или наличия частот в ряду распределения:
) – показывает средний разброс индивидуальных значений от среднего показателя без учета направленности по модулю. Его можно рассчитать как по формуле средней арифметической простой, так и по формуле средней арифметической взвешенной, в зависимоти от отсутствия или наличия частот в ряду распределения:
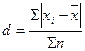 – невзвешенное среднее линейное отклонение (для несгруппированных данных);
– невзвешенное среднее линейное отклонение (для несгруппированных данных);
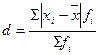 – взвешенное среднее линейное отклонение (для сгруппированных данных).
– взвешенное среднее линейное отклонение (для сгруппированных данных).
Дисперсия ( 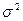 ) представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины. В зависимости от исходных данных дисперсия вычисляется по формуле средней арифметической простой или взвешенной:
) представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины. В зависимости от исходных данных дисперсия вычисляется по формуле средней арифметической простой или взвешенной:
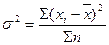 – невзвешенная (простая) дисперсия (для несгруппированных данных);
– невзвешенная (простая) дисперсия (для несгруппированных данных);
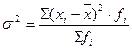 – взвешенная дисперсия (для сгруппированных данных).
– взвешенная дисперсия (для сгруппированных данных).
Среднее квадратическое отклонение 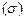 представляет собой корень квадратный из дисперсии:
представляет собой корень квадратный из дисперсии:
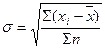 – невзвешенное среднее квадратическое отклонение (для несгруппированных данных);
– невзвешенное среднее квадратическое отклонение (для несгруппированных данных);
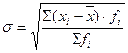 – взвешенное среднее квадратическое отклонение (для сгруппированных данных).
– взвешенное среднее квадратическое отклонение (для сгруппированных данных).
Размах вариации, среднее линейное отклонение и среднее квадратическое отклонение являются величинами именованными. Они имеют те же единицы измерения, что и индивидуальные значения признака.
Для сравнения размеров вариации различных признаков, а также для сравнения степени вариации одноименных признаков в нескольких совокупностях исчисляется относительный показатель вариации – коэффициент вариации ( 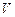 ), который представляет собой процентное отношение среднего квадратического отклонения к средней арифметической:
), который представляет собой процентное отношение среднего квадратического отклонения к средней арифметической:
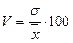 .
.
По величине коэффициента вариации можно судить о степени вариации признаков, а следовательно, об однородности состава совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу. Совокупность считается однородной, если коэффициент вариации не превышает 33 %.
Задача 2.3.1
Имеются данные о стаже работы служащих в филиалах коммерческого банка за отчетный год:
| Филиал | Стаж работы, лет | Число служащих, чел. |
| 1 | До 3 | 10 |
| 2 | 3-5 | 48 |
| 3 | 5-7 | 28 |
| 4 | 7-9 | 10 |
| 5 | Свыше 9 | 4 |
Рассчитайте все показатели вариации. Решение оформите в таблице. Объясните экономический смысл полученных результатов. Проанализируйте динамику вариации, если коэффициент вариации в прошлом году равнялся 39 %.
Решение.
Показатели вариации:
1. Размах вариации: 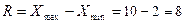 лет. Заметим, что размах вариации необходимо находить по несгруппированным данным, что уже сделано нами при расчете величины интервала в таблице 3.1, графа 3.
лет. Заметим, что размах вариации необходимо находить по несгруппированным данным, что уже сделано нами при расчете величины интервала в таблице 3.1, графа 3.
2. Среднее значение признака (определяется по формуле средней арифметической взвешенной): 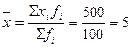 лет.
лет.
3. Среднее линейное отклонение: 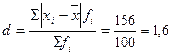 лет.
лет.
Таким образом, среднее отклонение индивидуального стажа работы служащих от среднего стажа работы в целом по филиалам коммерческого банка за отчетный год без учета знаков составило 1,6 лет.
4. Дисперсия: 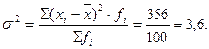
5. Среднее квадратическое отклонение:
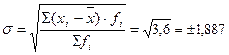 лет.
лет.
Таким образом, индивидуальное значение стажа работы служащих по филиалам коммерческого банка за отчетный год отклоняются от среднего показателя в пределах 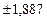 лет.
лет.
6. Коэффициент вариации: 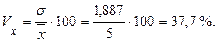
Таким образом, стаж служащих по филиалам коммерческого банка за отчетный год отличается от среднего стажа ( 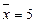 ) в среднем на 1,9 года, или на 37,7 %. Значение коэффициента вариации превышает 33 %, следовательно, вариация стажа работы служащих велика, найденный средний стаж плохо представляет всю совокупность служащих, не является ее типичной, надежной характеристикой, а саму совокупность нет оснований считать однородной по стажу работы служащих.
) в среднем на 1,9 года, или на 37,7 %. Значение коэффициента вариации превышает 33 %, следовательно, вариация стажа работы служащих велика, найденный средний стаж плохо представляет всю совокупность служащих, не является ее типичной, надежной характеристикой, а саму совокупность нет оснований считать однородной по стажу работы служащих.
7. Анализ динамики вариации: 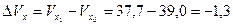 %.
%.
Таким образом, совокупность служащих филиалов коммерческого банка за два года по стажу стала более однородной, так как уменьшилась вариация на –1,3 %.
Таблица 3.1 – Исходные и расчетные данные для определения показателей вариации служащих по стажу работы в филиалах коммерческого банка за отчетный год
| Филиал | Стаж работы, лет | Число служащих, чел.
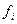
| Середина интервала
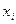
| 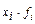
| 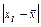
| 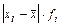
| 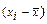
| 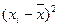
|
|
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | До 3 | 10 | 2 | 20 | 3 | 30 | -3 | 9 | 90 |
| 2 | 3-5 | 48 | 4 | 192 | 1 | 48 | -1 | 1 | 48 |
| 3 | 5-7 | 28 | 6 | 168 | 1 | 28 | 1 | 1 | 28 |
| 4 | 7-9 | 10 | 8 | 80 | 3 | 30 | 3 | 9 | 90 |
| 5 | Свыше 9 | 4 | 10 | 40 | 5 | 20 | 5 | 25 | 100 |
| Итого | 100 | - | 500 | - | 156 | - | - | 356 | |
Дата: 2018-12-28, просмотров: 382.