Важнейшим этапом исследования социально-экономических явлений и процессов является систематизация первичных данных и получение на этой основе сводной характеристики объекта в целом при помощи обобщающих показателей, что достигается путем сводки и группировки первичного статистического материала.
Сводка это комплекс последовательных операций по обобщению конкретных единичных фактов, образующих совокупность, для выявления типичных черт и закономерностей, присущих изучаемому явлению в целом.
По глубине и точности обработки материала различают сводку простую и сложную.
Простая сводка – это операция по подсчету общих итогов по совокупности единиц наблюдения.
Сложная сводка – это комплекс операций, включающих группировку единиц наблюдения, подсчет итогов по каждой группе и по всему объекту и представление результатов группировки и сводки в виде статистических таблиц.
Проведение сложной сводки необходимо осуществлять по следующим этапам:
· выбор группировочного признака;
· определение порядка формирования групп;
· разработка системы статистических показателей для характеристики групп и объекта в целом;
· разработка макетов статистических таблиц.
Группировкой статистических данных называется разделение сложного массового явления на однородные группы в качественном отношении по каким-либо существенным признакам.
Различают следующие виды статистических группировок:
· типологическая группировка – это разделение исследуемой качественно разнородной совокупности на классы, социально-экономические типы, однородные группы единиц в соответствии с правилами научной группировки;
· структурная группировка – это группировка, в которой происходит разбиение однородной совокупности на группы, характеризующие ее структуру по какому-либо варьирующему признаку;
· аналитическая группировка – это группировка, выявляющая взаимосвязи между изучаемыми явлениями и их признаками. Взаимосвязь проявляется в том, что с возрастанием значения факторного признака систематически возрастает или убывает среднее значение результативного признака. Особенности аналитической группировки: в основу группировки кладется факторный признак; каждая выделенная группа характеризуется средними значениями результативного признака.
Факторными называются признаки, оказывающие влияние на изменение результативных. Результативными называются признаки, изменяющиеся под влиянием факторных.
Порядок проведения статистической группировки может быть осуществлен в следующей последовательности:
· первоначально необходимо решить вопрос о выборе группировочного признака, по которому проводится разбивка единиц совокупности на отдельные группы. В основание группировки могут быть положены как количественные, так и атрибутивные признаки (количественные признаки имеют числовое выражение, атрибутивные – отражают состояние единицы совокупности);
· определение числа групп. Если группировка строится по атрибутивному признаку, то число групп, определяется количеством градаций, видов состояний у этого признака. Если группировка проводится по количественному признаку, то число групп зависит от числа единиц исследуемого объекта и степени колеблемости группировочного признака. Определение числа групп можно осуществить и по формуле Стерджесса:
,
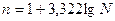где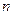 
– число групп, 
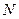– число единиц совокупности.
· определение интервала группировки.
Интервал – это значение варьирующего признака, лежащее в определенных границах. Каждый интервал имеет свою величину, верхнюю и нижнюю границы или хотя бы одну из них. Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей – наибольшее значение признака в интервале. Величина интервала представляет собой разность между верхней и нижней границами интервала.
Интервалы группировки в зависимости от их величины бывают равные и неравные. Величина равного интервала определяется по формуле: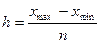 
, где 
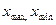– максимальное и минимальное значения признака.
Если размах вариации признака велик и его значения варьируются неравномерно, то необходимо использовать группировку с неравными интервалами.
Неравные интервалы могут быть прогрессивно-возрастающими или прогрессивно-убывающими в арифметической или геометрической прогрессии. Величина интервалов, изменяющихся в арифметической прогрессии определяется следующим образом: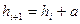 
, где 
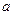– константа, имеющая для прогрессивно-возрастающих интервалов знак «+», а для прогрессивно-убывающих интервалов «–»; а в геометрической прогрессии: 
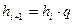, где 
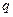– константа (для прогрессивно-убывающих интервалов 
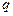>1; в другом случае 
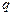<1).
Применение неравных интервалов обусловлено тем, что в первых группах небольшая разница в показателях имеет большое значение, а в последних группах разница несущественна.
Интервалы группировок могут быть закрытыми и открытыми. Закрытые интервалы – это обычные интервалы, имеющие как нижние (т. е. «от»), так и верхние (т. е. «до») границы. Открытые интервалы – это интервалы, имеющие какую-либо одну границу – верхнюю или нижнюю.
Группировку начинают с наименьшего значения группировочного признака, последовательно прибавляя значение интервала. При этом необходимо использовать принцип единообразия: левая граница включает в себя обозначенное значение, а правая – не включает.
Задача 2.1.1
Имеются данные о среднегодовой стоимости основных производственных фондов, среднесписочной численности работающих и производстве продукции по 24 предприятиям одной из отраслей промышленности за отчетный период:
| Номер пред-приятия | Среднегодовая стоимость основных производственных фондов, млн. руб. | Среднесписочное число работающих за отчетный период, чел. | Производство продукции за отчетный период, млн. руб. |
| 1 | 3,0 | 360 | 3,2 |
| 2 | 7,0 | 380 | 9,6 |
| 3 | 2,0 | 230 | 1,5 |
| 4 | 3,9 | 470 | 4,2 |
| 5 | 3,3 | 395 | 6,4 |
| 6 | 2,8 | 280 | 2,8 |
| 7 | 6,5 | 580 | 9,4 |
| 8 | 6,6 | 200 | 11,9 |
| 9 | 2,0 | 270 | 2,5 |
| 10 | 4,7 | 340 | 3,5 |
| 11 | 2,7 | 200 | 2,3 |
| 12 | 3,3 | 250 | 1,3 |
| 13 | 3,0 | 310 | 1,4 |
| 14 | 3,1 | 410 | 3,0 |
| 15 | 3,2 | 635 | 2,5 |
| 16 | 3,6 | 400 | 7,9 |
| 17 | 3,1 | 310 | 3,6 |
| 18 | 5,6 | 480 | 8,0 |
| 19 | 3,5 | 300 | 2,5 |
| 20 | 4,0 | 350 | 2,8 |
| 21 | 1,0 | 330 | 1,6 |
| 22 | 7,0 | 260 | 12,9 |
| 23 | 4,5 | 435 | 5,6 |
| 24 | 4,9 | 505 | 4,4 |
На основе приведенных данных построить структурную и аналитическую группировки предприятий промышленности по числу работающих, образовав пять групп с равными интервалами.
Результаты представьте в табличной форме.
Сформулируйте выводы.
Решение.
По условию задачи группировочным признаком является численность работающих предприятий одной из отраслей промышленности, число групп составляет 5.
Тогда, величину равного интервала можно определить по формуле:
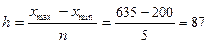чел.
Отсюда, путем прибавления величины интервала к минимальному уровню признака в группе получим следующие группы предприятий промышленности по числу работающих:
· первая группа 200–287 человек;
· вторая группа 287–374 человек;
· третья группа 374–461 человек;
· четвертая группа 461–548 человек;
· пятая группа 548–635 человек.
Распределим предприятия одной из отраслей промышленности по указанным группам, при этом необходимо использовать принцип единообразия: левая граница включает в себя обозначенное значение, а правая не включает (последняя группа включает в себя и левую и правую границу) и подсчитаем итоги по каждой группе.
Результаты группировки оформим в таблице 1.1.
Таблица 1.1 – Распределение предприятий промышленности по числу работающих
| Номер группы | Группы предприятий по числу работающих, чел. | Номер предприятия | Среднегодовая стоимость основных производственных фондов, млн. руб. | Среднесписочное число работающих за отчетный пе-риод, чел. | Производство продукции за отчетный период, млн. руб. |
| А | Б | 1 | 2 | 3 | 4 |
|
1 |
200-287
| 3 | 2,0 | 230 | 1,5 |
| 6 | 2,8 | 280 | 2,8 | ||
| 8 | 6,6 | 200 | 11,9 | ||
| 9 | 2,0 | 270 | 2,5 | ||
| 11 | 2,7 | 200 | 2,3 | ||
| 12 | 3,3 | 250 | 1,3 | ||
| 22 | 7,0 | 260 | 12,9 | ||
Итого
2
287-374
Итого
3
374-461
Итого
4
461-548
Итого
5
548-635
Итого
Всего
Структурную группировку представим в таблице 1.2.
Таблица 1.2 – Структурная группировка предприятий промышленности по числу работающих
| Номер группы | Группы предприятий по числу работающих, чел. | Количество предприятий, в % к итогу | Среднегодовая стоимость основных производственных фондов, в % к итогу | Средне-списочное число работающих за отчетный период, в % к итогу | Производство продукции за отчетный период, в % к итогу |
| 1 | 200-287 | 29,2 | 28,0 | 19,5 | 30,7 |
| 2 | 287-374 | 29,2 | 23,6 | 26,5 | 16,2 |
| 3 | 374-461 | 20,8 | 22,8 | 23,3 | 28,3 |
| 4 | 461-548 | 12,5 | 15,3 | 16,8 | 14,5 |
| 5 | 548-635 | 8,3 | 10,3 | 14,0 | 10,4 |
| Итого | 100,0 | 100,0 | 100,0 | 100,0 | |
Таким образом, данные таблицы 1.2 показывают, что наибольший удельный вес 29,2 % приходится на предприятия первой и второй групп; 20,8 % всех предприятий приходится на третью группу; четвертая и пятая группы являются самыми малочисленными – они составляют 12,5 % и 8,3 % соответственно.
Анализ взаимосвязи показателей можно сделать на основе аналитической группировки (таблица 1.3).
Таблица 1.3 – Аналитическая группировка предприятий промышленности по числу работающих
| Номер группы | Группы предприятий по числу работающих, чел. | Коли-чество пред-приятий, ед. | Среднегодовая стоимость основных производственных фондов, млн. руб. | Производство продукции за отчетный период, млн. руб. | ||
| всего | в среднем на одно предприятие | всего | в среднем на одно предприятие | |||
| А | Б | 1 | 2 | 3 | 4 | 5 |
| 1 | 200 – 287 | 7 | 26,4 | 3,8 | 35,2 | 5,0 |
| 2 | 287 – 374 | 7 | 22,3 | 3,2 | 18,6 | 2,7 |
| 3 | 374 – 461 | 5 | 21,5 | 4,3 | 32,5 | 6,5 |
| 4 | 461 – 548 | 3 | 14,4 | 4,8 | 16,6 | 5,5 |
| 5 | 548 – 635 | 2 | 9,7 | 4,9 | 11,9 | 6,0 |
| Итого | 24 | 94,3 | – | 114,8 | – | |
| В среднем на 1 предприятие | – | – | 3,9 | – | 4,8 | |
Среднесписочное число работающих за отчетный период –
факторный признак, среднегодовая стоимость основных производственных фондов и производство продукции – результативный признак.
Таким образом, сравнивая графы 3 и 5 в таблице 1.3, видим, что с ростом численности работающих наблюдается увеличение стоимости основных производственных фондов, что говорит о прямой зависимости между указанными признаками, чего нельзя сказать о признаках выпуска продукции и численности работающих.
Дата: 2018-12-28, просмотров: 240.
