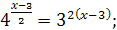Цель: формирование навыков решения показательных и логарифмических уравнений, используя различные приемы.
Вид работы: индивидуальный.
Время выполнения: 2 часа.
Теоретические сведения
Уравнения, в которых неизвестное содержится в показатели степени, называются показательными.
Решение показательных уравнений часто сводится к решению уравнения 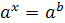 , где
, где 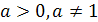 ,
, 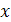 - неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием
- неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием 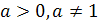 равны тогда и только тогда, когда равны их показатели.
равны тогда и только тогда, когда равны их показатели.
Решение показательных неравенств часто сводится к решению неравенств 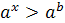 или
или 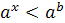 . Эти неравенства решаются с помощью свойства возрастания или убывания показательной функции: для возрастающей функции большему значению функции соответствует большее значение аргумента, а для убывающей функции большему значению функции соответствует меньшее значение аргумента.
. Эти неравенства решаются с помощью свойства возрастания или убывания показательной функции: для возрастающей функции большему значению функции соответствует большее значение аргумента, а для убывающей функции большему значению функции соответствует меньшее значение аргумента.
Пример 1. Решите уравнение 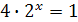 .
.
Решение. Запишем уравнение в виде 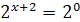 , откуда
, откуда 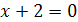 . Тогда
. Тогда 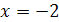 .
.
Ответ: 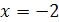 .
.
Пример 2. Решите уравнение 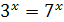 .
.
Решение. Так как 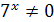 , то уравнение можно записать в виде
, то уравнение можно записать в виде 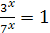 , откуда
, откуда 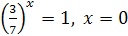 .
.
Ответ: x=0 .
Пример 3. Решите уравнение 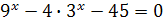 .
.
Решение. Заменой 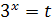 данное уравнение сводится к квадратному уравнению
данное уравнение сводится к квадратному уравнению 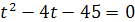 . Решая это уравнение, находим его корни:
. Решая это уравнение, находим его корни: 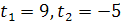 , откуда
, откуда 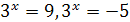 . Уравнение
. Уравнение 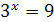 имеет корень
имеет корень 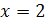 , а уравнение
, а уравнение 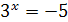 не имеет корней, так как показательная функция не может принимать отрицательные значения.
не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ: 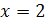 .
.
Пример 4. Решите графически уравнение 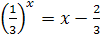 .
.
Решение. В одной системе координат построим графики функций 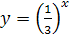 и
и 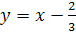 . Из рисунка видно, что графики этих функций пересекаются в точке с абсциссой
. Из рисунка видно, что графики этих функций пересекаются в точке с абсциссой 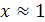 . Проверка показывает, что
. Проверка показывает, что 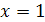 - корень данного уравнения:
- корень данного уравнения:
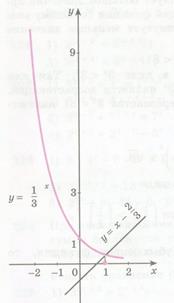 Рисунок 32.1 – графики
функций
Рисунок 32.1 – графики
функций
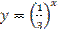 и и 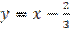
| 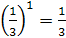 и и 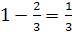 .
Ответ: .
Ответ: 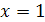 .
Покажем, что других корней нет. Функция .
Покажем, что других корней нет. Функция 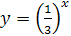 убывающая, а функция убывающая, а функция 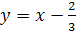 – возрастающая. Следовательно, при – возрастающая. Следовательно, при 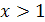 значение первой функции меньше значение первой функции меньше  , а второй больше , а второй больше  , при , при 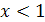 , наоборот, значения первой функции больше , наоборот, значения первой функции больше  , а второй меньше , а второй меньше  . Геометрически это означает, что графики этих функций при . Геометрически это означает, что графики этих функций при 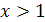 и и 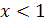 «расходятся» и потому не могут иметь точек пересечения при «расходятся» и потому не могут иметь точек пересечения при 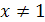 .
Уравнение, содержащее переменную под знаком логарифма или в основании логарифма, называется логарифмическим. .
Уравнение, содержащее переменную под знаком логарифма или в основании логарифма, называется логарифмическим.
|
При решении таких уравнений следует учитывать область определения и использовать определение логарифма.
Пример 5. Решите уравнение 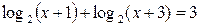 (32.1)
(32.1)
Решение. Предположим, что x – такое число, при котором равенство (1) является верным, т.е. x – корень уравнения (32.1). Тогда по свойству логарифма верно равенство: 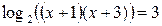 (32.2).
(32.2).
Из этого равенства по определению логарифма получаем 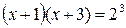
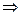
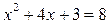 (3), т.е.
(3), т.е. 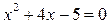 . Решая квадратное уравнение, получаем корни:
. Решая квадратное уравнение, получаем корни: 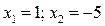 . Так как уравнение (32.3) является следствием исходного уравнения, то необходима проверка. Подставляем в левую часть исходного уравнения полученные корни:
. Так как уравнение (32.3) является следствием исходного уравнения, то необходима проверка. Подставляем в левую часть исходного уравнения полученные корни:
1. если x =1, то 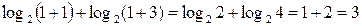 , равенство верно, значит x =1 – корень уравнения.
, равенство верно, значит x =1 – корень уравнения.
2. если x =-5, то 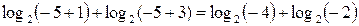 , по области определения логарифм от отрицательного числа не существует, значит x =-5 – не является корнем уравнения.
, по области определения логарифм от отрицательного числа не существует, значит x =-5 – не является корнем уравнения.
Ответ: 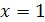 .
.
Решение уравнения (1) можно заменить решением равносильной ему системы: 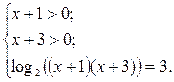
Пример 6. Решите уравнение 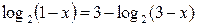 .
.
Решение. Перенесем логарифм из правой части в левую:
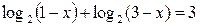
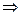
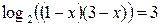
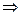
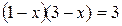 . Открываем скобки, решаем квадратное уравнение, получаем корни:
. Открываем скобки, решаем квадратное уравнение, получаем корни: 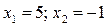 .
.
Проверка показывает, что только 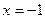 является корнем уравнения.
является корнем уравнения.
Ответ: 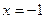 .
.
Пример 7. Решите уравнение 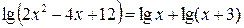 .
.
Решение. По свойству логарифмов: 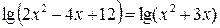
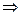
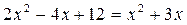
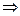
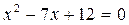
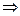
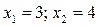 .
.
Проверка показывает, что оба корня являются корнями исходного уравнения.
Ответ: 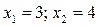 .
.
Пример 8. Решите уравнение 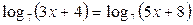
Решение: 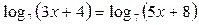
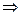
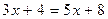
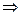
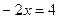
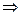
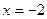
Выполняя проверку, видим, что выражения, стоящие под знаком логарифма при 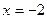 не имеют смысла.
не имеют смысла.
Ответ: корней нет.
Пример 9. Решите уравнение 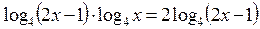
Решение: преобразовываем данное уравнение:
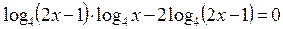 , вынесем за скобки общий множитель
, вынесем за скобки общий множитель
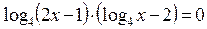 . Приравниваем каждый множитель левой части к нулю, решаем уравнения:
. Приравниваем каждый множитель левой части к нулю, решаем уравнения: 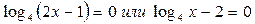 . Получаем:
. Получаем:
* 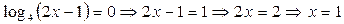 .
.
* 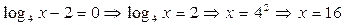
Проверка показывает, что оба значения являются корнями исходного уравнения.
Ответ: 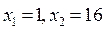 .
.
Пример 10. Решите уравнение 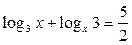
Решение: преобразовываем уравнение, используя формулу перехода к другому основанию 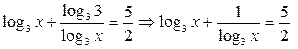 . Пусть
. Пусть 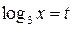 , тогда наше уравнение примет вид:
, тогда наше уравнение примет вид: 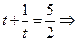
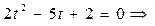
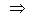
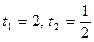 . Вернемся к замене:
. Вернемся к замене:
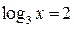 ; ;
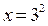 ; ;
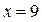 ОДЗ:
ОДЗ: 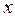 > 0; > 0; 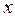 ≠1. ≠1.
| 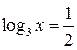 ; ;
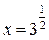 ; ;
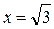
|
Найденные значения удовлетворяют ОДЗ.
Ответ: 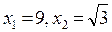 .
.
Задания к практической работе
Задание 1. Решите уравнение
| 1. | 2. | ||
| 3. | 4.
| ||
| 5. | 6.
| ||
| 7. | 8.
| ||
| 9. | 10.
| ||
| 11. | 12.
| ||
| 13. | 14.
| ||
| 15. | 16.
| ||
| 17. | 18. | ||
| 19. | 20.
| ||
| 21. | 22.
| ||
| 23. | 24.
| ||
25. 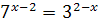 ; ;
| 26. | 27. 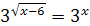 ; ;
| |
28. 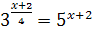 ; ;
| 29. | 30. 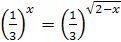 . .
| |
Задание 2. Решить графически уравнение:
1. 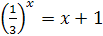 ; ;
| 2. 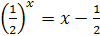 ; ;
|
3. 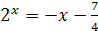 ; ;
| 4. 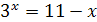 ; ;
|
5. 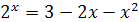 ; ;
| 6. 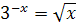 ; ;
|
7. 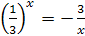 ; ;
| 8. 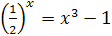 . .
|
Задание 3. Решите уравнения:
1. 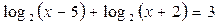 ; ;
| 2. 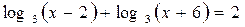 ; ;
|
3. 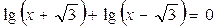 ; ;
| 4. 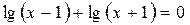 ; ;
|
5. 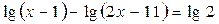 ; ;
| 6. 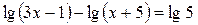 ; ;
|
7. 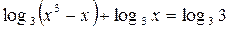 ; ;
| 8. 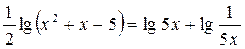 ; ;
|
9. 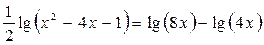 ; ;
| 10. 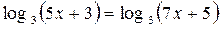 ; ;
|
11. 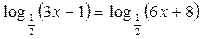 ; ;
| 12. 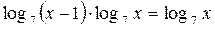 ; ;
|
13. 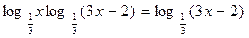 ; ;
| 14. 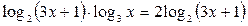 ; ;
|
15. 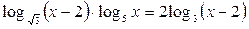 ; ;
| 16. 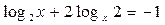 ; ;
|
17. 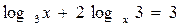 ; ;
| 18. 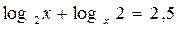
|
Контрольные вопросы
1. Дайте определение показательных уравнений. Приведите примеры.
2. Перечислите основные свойства показательной функции.
3. Какие простейшие приемы решения показательных уравнений вы знаете?
4. Дайте определение логарифма.
5. Назовите свойства логарифмов.
Рекомендуемая литература: 1.1, 2.1.
СПИСОК ЛИТЕРАТУРЫ
1. Основная:
1.1 Кремер, Н. Ш. Математика для колледжей : учебное пособие для
СПО / Н. Ш. Кремер, О. Г. Константинова, М. Н. Фридман ; под ред. Н. Ш. Кремера. — 10-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 346 с.
1.2 Богомолов, Н. В. Практические занятия по математике в 2 ч. Часть 1 : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 285 с.
1.3 Богомолов, Н. В. Практические занятия по математике в 2 ч. Часть 2 : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 217 с.
1.4 Богомолов, Н. В. Алгебра и начала анализа : учебное пособие для СПО / Н. В. Богомолов. — М. : Издательство Юрайт, 2018. — 200 с.
1.5 Далингер, В. А. Методика обучения стереометрии посредством решения задач : учебное пособие для СПО / В. А. Далингер. — 2-е изд., испр. и доп. — М. : Издательство Юрайт, 2018. — 370 с.
2. Дополнительная:
2.1 Шипачев, В. С. Математика : учебник и практикум для СПО / В. С. Шипачев ; под ред. А. Н. Тихонова. — 8-е изд., перераб. и доп. — М. : Издательство Юрайт, 2017. — 447 с.
2.2 Кремер, Н. Ш. Теория вероятностей и математическая статистика : учебник и практикум для академического бакалавриата / Н. Ш. Кремер. — 4-е изд., перераб. и доп. — М. : Издательство Юрайт, 2017. — 514 с.
Учебное издание
Дата: 2018-12-28, просмотров: 369.
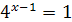 ;
;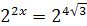 ;
;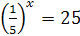 ;
;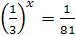 ;
;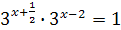 ;
;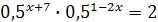 ;
;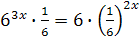 ;
;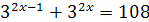 ;
;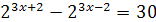 ;
;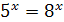 ;
;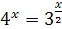 ;
;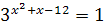 ;
;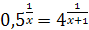 ;
;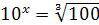 ;
; ;
;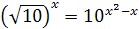 ;
;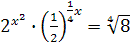 ;
;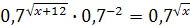 ;
;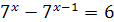 ;
;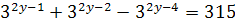 ;
;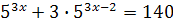 ;
;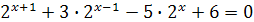 ;
;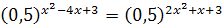 ;
;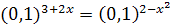 ;
;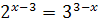 ;
;