Цель: формирование навыков решения уравнений, используя различные приемы.
Вид работы: индивидуальный.
Время выполнения: 2 часа.
Теоретические сведения
I. Уравнение 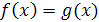 называется рациональным, если
называется рациональным, если 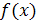 и
и 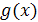 – рациональные выражения.
– рациональные выражения.
Чтобы решить рациональное уравнение, нужно:
1) найти общий знаменатель всех имеющихся дробей;
2) заменить данное уравнение целым, умножив обе его части на общий знаменатель;
3) решить полученное целое уравнение;
4) исключить из его корней те, которые обращают в нуль общий знаменатель.
Пример 1. Решите уравнение 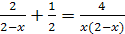 .
.
Решение. Общий знаменатель имеющихся дробей является 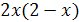 . Найдя дополнительные множители для каждой дроби, освободимся от знаменателей. Имеем:
. Найдя дополнительные множители для каждой дроби, освободимся от знаменателей. Имеем: 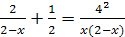 ;
;
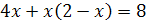
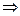
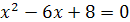 .
.
Из уравнения 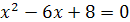 находим
находим 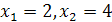 . Осталось проверить, обращают ли найденные корни в нуль выражение
. Осталось проверить, обращают ли найденные корни в нуль выражение 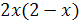 , т.е. проверить выполнение условия
, т.е. проверить выполнение условия 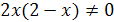 . Замечаем, что 2 не удовлетворяет этому условию, а 4 удовлетворяет. Значит,
. Замечаем, что 2 не удовлетворяет этому условию, а 4 удовлетворяет. Значит, 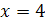 - единственный корень уравнения.
- единственный корень уравнения.
Решение уравнений 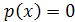 методом разложения его левой части на множители.
методом разложения его левой части на множители.
Суть этого метода состоит в том, что нужно решить уравнение 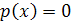 , где
, где 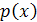 – многочлен степени
– многочлен степени 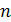 . Предположим, что нам удалось разложить многочлен на множители:
. Предположим, что нам удалось разложить многочлен на множители: 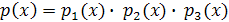 , где
, где 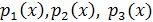 – многочлены более низкой степени, чем
– многочлены более низкой степени, чем 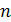 . Тогда уравнение
. Тогда уравнение 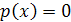 примет вид
примет вид 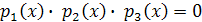 . Если
. Если 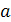 – корень уравнения
– корень уравнения 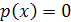 , то
, то 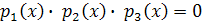 , а потому хотя бы одно из чисел
, а потому хотя бы одно из чисел 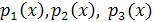 равно нулю. Значит
равно нулю. Значит 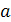 , - корень хотя бы одного из уравнений
, - корень хотя бы одного из уравнений
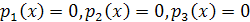 .
.
Итак, если 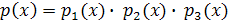 , где
, где 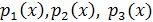 – многочлены, то вместо уравнения
– многочлены, то вместо уравнения 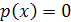 нужно решить совокупность уравнений
нужно решить совокупность уравнений 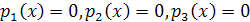 . Все найденные корни этих уравнений, и только они, будут корнями уравнения
. Все найденные корни этих уравнений, и только они, будут корнями уравнения 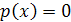 .
.
Пример 2. Решите уравнение 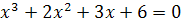 .
.
Решение. Разложим на множители левую часть уравнения. Имеем 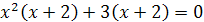 , откуда
, откуда 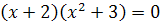 . Значит, либо
. Значит, либо 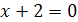 , либо
, либо 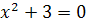 . Из первого уравнения находим
. Из первого уравнения находим 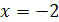 , второе уравнение корней не имеет. Таким образом, корень уравнения -2.
, второе уравнение корней не имеет. Таким образом, корень уравнения -2.
Решение уравнений методом введения новой переменной
Суть этого метода поясним на примере.
Пример 3. Решите уравнение 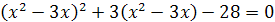 .
.
Решение. Положив 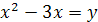 , получим уравнение
, получим уравнение 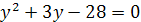 , откуда находим
, откуда находим 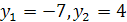 . Теперь задача сводится к решению совокупности уравнений:
. Теперь задача сводится к решению совокупности уравнений: 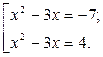
Первое квадратное уравнение не имеет действительных корней, так как его дискриминант отрицателен.
Из второго квадратного уравнения находим 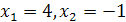 . Это действительные корни заданного уравнения.
. Это действительные корни заданного уравнения.
Биквадратные уравнения
Биквадратным называется уравнение вида 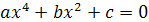 , где
, где 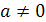 . Биквадратное уравнение решается методом введения новой переменной: положив
. Биквадратное уравнение решается методом введения новой переменной: положив 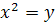 , придем к квадратному уравнению
, придем к квадратному уравнению 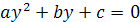 .
.
Пример 4. Решите уравнение 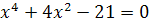 .
.
Решение. Положив 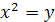 , получим квадратное уравнение
, получим квадратное уравнение 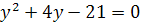 , откуда находим
, откуда находим 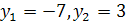 . Теперь задача сводится к решению уравнений
. Теперь задача сводится к решению уравнений 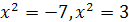 . Первое уравнение не имеет действительных корней, из второго находим
. Первое уравнение не имеет действительных корней, из второго находим 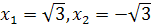 , которые являются корнями заданного биквадратного уравнения.
, которые являются корнями заданного биквадратного уравнения.
Решение задач с помощью составления уравнений
С помощью уравнений решаются многочисленные задачи, к которым приводят самые разнообразные вопросы физики, механики, экономики и многих других прикладных наук. Прежде всего напомним общий порядок решения задач с помощью уравнений.
1) Вводят переменные, т.е. буквами 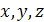 обозначают неизвестные величины, которые либо требуется найти в задаче, либо они необходимы для отыскания искомых величин.
обозначают неизвестные величины, которые либо требуется найти в задаче, либо они необходимы для отыскания искомых величин.
2) С помощью введенных переменных и данных в задаче чисел и их соотношений составляют уравнение.
3) Решают составленное уравнение и из полученных решений отбирают те, которые подходят по смыслу задачи.
4) Если буквами 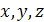 обозначили не искомые величины, то с помощью полученных решений находят ответ на вопрос задачи.
обозначили не искомые величины, то с помощью полученных решений находят ответ на вопрос задачи.
II. В уравнениях 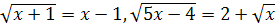 неизвестное
неизвестное 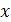 находится под знаком корня или под знаком возведения в дробную степень. Такие уравнения называют иррациональными.
находится под знаком корня или под знаком возведения в дробную степень. Такие уравнения называют иррациональными.
Решение иррациональных уравнений основано на следующем свойстве:
При возведении обеих частей уравнения в натуральную степень получается уравнение-следствие данного.
При возведении уравнения в натуральную степень могут появиться посторонние корни, поэтому необходимо делать проверку.
Если обе части уравнения 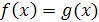 неотрицательны на множестве
неотрицательны на множестве 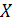 , то уравнение
, то уравнение 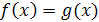 равносильно уравнению
равносильно уравнению 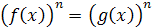 при
при 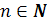 .
.
Пример 5 . Решите уравнение 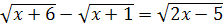 .
.
Решение. Возводя обе части уравнения в квадрат, получаем
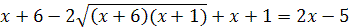
откуда 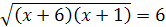 .
.
Возведем последнее уравнение в квадрат: 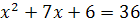 , или
, или 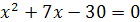 .
.
Корни этого уравнения 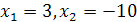 .
.
Проверка показывает, что 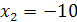 – посторонний корень.
– посторонний корень.
Ответ: 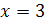 .
.
Пример 6 . Решите уравнение 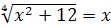 .
.
Решение. Возведем уравнение в четвертую степень: 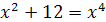 , откуда
, откуда 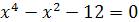 . Решим это биквадратное уравнение,
. Решим это биквадратное уравнение, 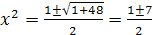 , т.е.
, т.е. 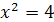 или
или 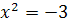 .
.
Уравнение 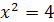 имеет два корня
имеет два корня 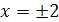 . Уравнение
. Уравнение 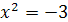 не имеет действительных корней. Так как при возведении обеих частей уравнения в четвертую степень могли появится посторонние корни, то нужно сделать проверку. При
не имеет действительных корней. Так как при возведении обеих частей уравнения в четвертую степень могли появится посторонние корни, то нужно сделать проверку. При 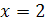 обе части уравнения равны 2, т.е.
обе части уравнения равны 2, т.е. 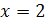 – корень уравнения. При
– корень уравнения. При 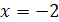 левая часть уравнения равна 2, а правая равна -2, т.е. -2 не является корнем уравнения.
левая часть уравнения равна 2, а правая равна -2, т.е. -2 не является корнем уравнения.
Ответ: 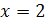 .
.
Пример 7. Решите уравнение 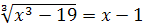 .
.
Решение. Возводя обе части уравнения в куб, получаем 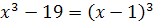 , откуда
, откуда
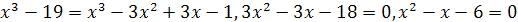 .
.
Корни этого уравнения 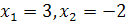 . Проверка показывает, что оба значения неизвестного являются корнями данного уравнения.
. Проверка показывает, что оба значения неизвестного являются корнями данного уравнения.
Пример 8. Выясните с помощью графиков, сколько корней имеет уравнение 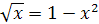 . Найти приближенные значения этих корней.
. Найти приближенные значения этих корней.
Решение. Построим на одном рисунке графики функций 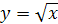 и
и 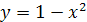 . Графики пересекаются в одной точке при
. Графики пересекаются в одной точке при 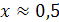 .
.
Задания к практической работе
Задание 1. Решите уравнения методом введения новой переменной:
1) 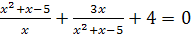 ;
;
2) 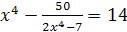 ;
;
3) 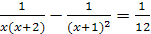 ;
;
4) 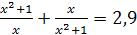 ;
;
5) 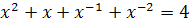 ;
;
6) 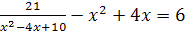 .
.
Задание 2. Решите уравнение, разложив левую часть на множители:
1) 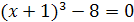 ;
;
2) 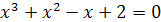 ;
;
3) 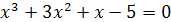 ;
;
4) 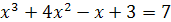 .
.
Задание 3. Решите задачу, составив к нему уравнение.
Для перевозки 60 т груза из одного места в другое затребовали некоторое количество машин. Ввиду неисправности дороги на каждую машину пришлось грузить на 0,5 т меньше, чем предполагалось, поэтому дополнительно потребовались 4 машины. Какое количество машин было затребовано?
Задание 4. Решите задачу, составив к нему уравнение.
Моторная лодка, обладающая скоростью движения 20 км/ч, прошла расстояние между двумя пунктами по реке туда и обратно без остановок за 6ч 15 мин. Расстояние между пунктами равно 60 км. Найти скорость течения реки.
Задание 5. Решите задачу, составив к нему уравнение.
Найти двухзначное число, зная, что цифра его единиц на 2 больше цифры десятков и что произведение искомого числа на сумму его цифр равно 144.
Задание 6. Решите задачу, составив к нему уравнение.
По обе стороны улицы, длиной в 1200 м, во вновь разбиваемом поселке лежат прямоугольные полосы земли, отведенные на участки, одна – шириной в 50 м, а другая – в 60 м. на сколько участков разбит весь поселок, если более узкая полоса содержит на 5 участков больше, чем широкая, при условии, что на узкой полосе каждый участок на 1200 м2 меньше, чем каждый участок на широкой полосе?
Задание 7. Решите задачу, составив к нему уравнение.
Через час после начала равномерного спуска воды в бассейне ее осталось 400 м3, а еще через три часа – 250 м3. Сколько воды было в бассейне?
Задание 8. Решите уравнение:
1. 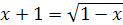 ; ;
| 2. | |
3. 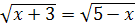 ; ;
| 4. | |
5. 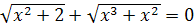 ; ;
| 6. | |
7.  ; ;
| 8. | |
9. 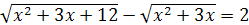 ; ;
| 10. | |
11. 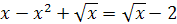 ; ;
| 12. | |
| 13.
| ||
| 14.
| 15. 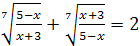 ; ;
| |
Задание 2. Выясните с помощью графиков, сколько корней имеет уравнение:
1. 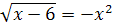 ; ;
| 2. 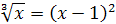 ; ;
|
3. 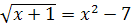 ; ;
| 4. 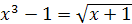 . .
|
Контрольные вопросы
1. Какие уравнения называют рациональными? Приведите примеры.
2. Назовите основные приемы решения рациональных уравнений.
3. Дайте определение биквадратным уравнениям.
4. Назовите алгоритм решения задач с помощью уравнений.
5. Дайте определение иррационального уравнения.
6. Какими методами можно решить иррациональные уравнения?
7. Каким методом можно решить уравнение 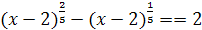 .
.
Рекомендуемая литература: 1.1, 1.4, 2.1
Практическая работа №31
Дата: 2018-12-28, просмотров: 364.
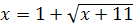 ;
;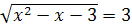 ;
;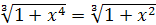 ;
;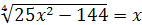 ;
;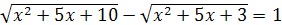 ;
;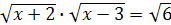 ;
;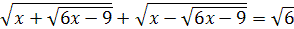 ;
;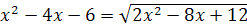 ;
;