Основными критериями оценки выполненной обучающимся и представленной для проверки работы являются:
1. Степень соответствия выполненного задания поставленным требованиям.
2. Структурирование и комментирование практической работы.
3. Уникальность выполнение работы (отличие от работ коллег).
4. Успешные ответы на контрольные вопросы.
«отлично» - оформление соответствует требованиям, критерии выдержаны, защита всего перечня контрольных вопросов.
«хорошо» - оформление соответствует требованиям, критерии выдержаны, защита только 80 % контрольных вопросов.
«удовлетворительно» - оформление соответствует требованиям, критерии выдержаны, защита только 61 % контрольных вопросов.
Практическая работа №27
Тема: Исследование функции. Свойства линейной, квадратичной, кусочно-линейной функций. Непрерывные и периодические функции. Свойства и графики синуса, косинуса и котангенса
Цель: формирование навыков нахождения области определения функций, и вычисления частных значений функций; построения графиков функций; построения графиков основных тригонометрических функций, определения их области определения и множества значений.
Вид работы: индивидуальный.
Время выполнения: 6 часов.
Теоретические сведения
Переменная y называется функцией переменной x, если каждому допустимому значению x соответствует определенное значение y.
Символически функциональная зависимость между переменной y (функцией) и переменной x (аргументом) записывается с помощью равенства y = f ( x ), где f обозначает совокупность действий, которые надо произвести над x, чтобы получить y.
Областью определения функции D ( y ) называется множество всех действительных значений аргумента x (множество всех точек числовой оси), при которых она имеет действительное значение.
Множеством значений функции E ( y ) называется множество всех действительных значений функции y, которые она может принимать.
Функция может быть задана аналитически (формулой), таблицей, графиком или каким-либо другим способом.
Функцию y = f ( x ) иногда можно представить таблицей, в первой строке которой перечисляются значения независимой переменной x, а во второй – соответствующие значения f ( x ) зависимой переменной.
Графиком функции y = f ( x ) называется множество всех точек координатной плоскости с координатами ( x ; f ( x )).
Известны графики многих функций. Например, график функции y = kx + b есть прямая линия (рис. 27.1), график функции y = x 2 – парабола (рис. 27.2), график функции 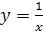 (обратная пропорциональная зависимость) – гипербола (рис. 27.3).
(обратная пропорциональная зависимость) – гипербола (рис. 27.3).
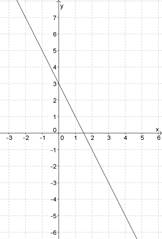 Рисунок 27.1 – график функции
y= kx+ b ( k<0)
Рисунок 27.1 – график функции
y= kx+ b ( k<0)
|
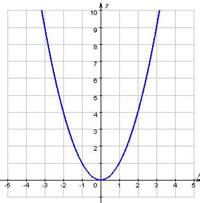 Рисунок 27.2 –
график функции y= x2
Рисунок 27.2 –
график функции y= x2
|
 Рисунок 27.3 – график функции
Рисунок 27.3 – график функции 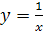
|
В графике содержится вся информация о функции.
Функция f (х) называется возрастающей на данном числовом промежутке Х, если большему значению аргумента 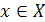 соответствует большее значение функции
соответствует большее значение функции 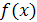 , т. е. для любых
, т. е. для любых 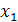 и
и 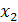 из промежутка X, таких, что
из промежутка X, таких, что 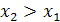 , выполнено неравенство
, выполнено неравенство 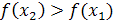 .
.
Функция f (х) называется убывающей на данном числовом промежутке X, если большему значению аргумента 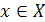 соответствует меньшее значение функции f (х), т. е. для любых
соответствует меньшее значение функции f (х), т. е. для любых 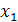 и
и 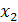 из промежутка X, таких, что
из промежутка X, таких, что 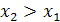 , выполнено неравенство
, выполнено неравенство 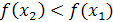 .
.
Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.
Функция y = f(x) называется четной, если она обладает следующими двумя свойствами:
1) область определения этой функции симметрична относительно точки О (т. е. если точка а принадлежит области определения, то точка - а также принадлежит области определения);
2) для любого значения х, принадлежащего области определения этой функции, выполняется равенство 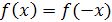 .
.
Функция y = f(x) называется нечетной, если:
1) область определения этой функции симметрична относительно точки О;
2) для любого значения 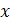 , принадлежащего области определения этой функции, выполняется равенство
, принадлежащего области определения этой функции, выполняется равенство 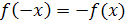 .
.
Функция f называется периодической, если существует такое число 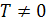 , что при любом х из области определения функции числа
, что при любом х из области определения функции числа 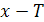 и
и 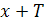 также принадлежат этой области и выполняется равенство
также принадлежат этой области и выполняется равенство 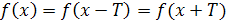 . В этом случае число Т называется периодом функции f.
. В этом случае число Т называется периодом функции f.
Если 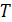 - период функции, то
- период функции, то 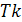 , где
, где 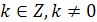 , также период функции. Следовательно, всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.
, также период функции. Следовательно, всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.
Функция 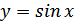
Основные свойства функции 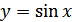 :
:
а) область определения – множество всех действительных чисел;
б) множество значений – отрезок 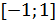 , значит, синус – функция ограниченная;
, значит, синус – функция ограниченная;
в) функция нечетная: 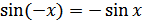 для всех
для всех 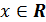 ;
;
г) функция периодическая с наименьшим положительным периодом 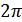 , т.е.
, т.е. 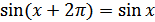 для всех
для всех 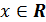 ;
;
д) 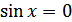 при
при 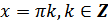 ;
;
е) 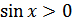 для всех
для всех 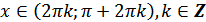 ;
;
ж) 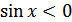 для всех
для всех 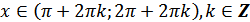 ;
;
з) функция возрастает от -1 до 1 на промежутках 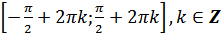 ;
;
и) функция убывает от 1 до -1 на промежутках 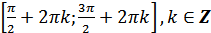 ;
;
к) функция принимает наибольшее значение, равное 1, в точках 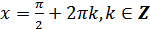 ;
;
л) функция принимает наименьшее значение, равное -1, в точках 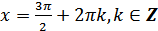 .
.
График функции 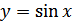 изображен на рисунке 27.4. Кривая, являющаяся графиком функции
изображен на рисунке 27.4. Кривая, являющаяся графиком функции 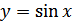 , называется синусоидой.
, называется синусоидой.
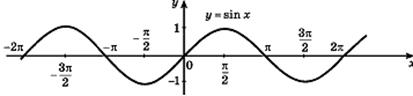
Рисунок 27.4 – график функции 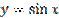
Функция 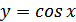
Основные свойства функции 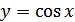 :
:
а) область определения – множество всех действительных чисел;
б) множество значений – отрезок 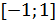 , значит, косинус – функция ограниченная;
, значит, косинус – функция ограниченная;
в) функция четная: 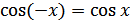 для всех
для всех 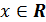 ;
;
г) функция периодическая с наименьшим положительным периодом 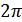 , т.е.
, т.е. 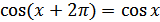 для всех
для всех 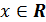 ;
;
д) 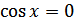 при
при 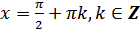 ;
;
е) 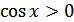 для всех
для всех 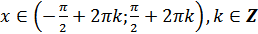 ;
;
ж) 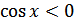 для всех
для всех 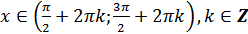 ;
;
з) функция убывает от -1 до 1 на промежутках 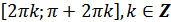 ;
;
и) функция возрастает от 1 до -1 на промежутках 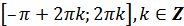 ;
;
к) функция принимает наибольшее значение, равное 1, в точках 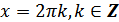 ;
;
л) функция принимает наименьшее значение, равное -1, в точках 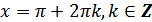 .
.
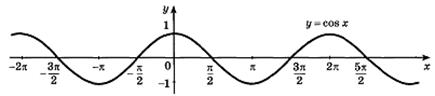
Рисунок 27.5 – график функции 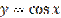
Функция 
Основные свойства функции 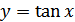 :
:
а) область определения – множество всех действительных чисел, кроме чисел вида 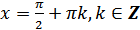 ;
;
б) множество значений – вся числовая прямая, таким образом, тангенс – функция неограниченная;
в) функция нечетная: 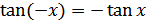 для всех
для всех 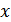 из области определения;
из области определения;
г) функция периодическая с наименьшим положительным периодом 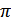 , т.е.
, т.е. 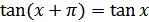 для всех
для всех 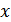 из области определения;
из области определения;
д) 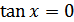 при
при 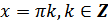 ;
;
е) 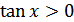 для всех
для всех 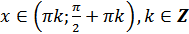 ;
;
ж) 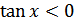 для всех
для всех 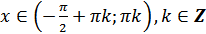 ;
;
з) функция возрастает на промежутках 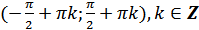 .
.
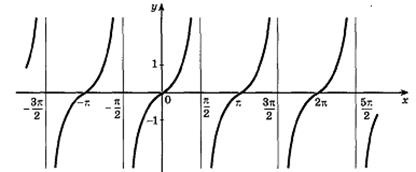
Рисунок 27.6 – график функции 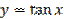
Функция 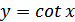
Основные свойства функции 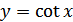 :
:
а) область определения – множество всех действительных чисел, кроме чисел вида 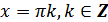 ;
;
б) множество значений – вся числовая прямая, таким образом, котангенс – функция неограниченная;
в) функция нечетная: 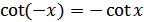 для всех
для всех 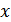 из области определения;
из области определения;
г) функция периодическая с наименьшим положительным периодом 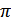 , т.е.
, т.е.  для всех
для всех 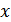 из области определения;
из области определения;
д)  при
при 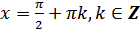 ;
;
е) 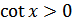 для всех
для всех 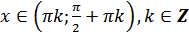 ;
;
ж) 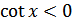 для всех
для всех 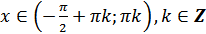 ;
;
з) функция убывает на каждом из промежутков 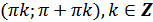 .
.
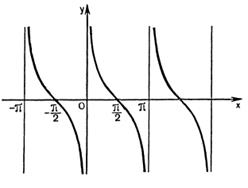
Рисунок 27.7 – график функции 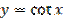
Пример 1. Дана функция 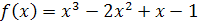 .
.
Найдите 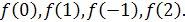
Решение. Чтобы вычислить значение 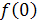 , необходимо в данную функцию вместо аргумента x подставить его значение
, необходимо в данную функцию вместо аргумента x подставить его значение  . Имеем
. Имеем 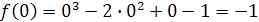 .
.
Аналогично получим 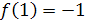 ,
, 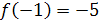 и
и 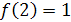 .
.
Пример 2. Найдите область определения функции:
1) 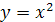 ;
;
2) 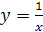 ;
;
3) 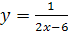 ;
;
4) 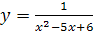 ;
;
5)  ;
;
6) 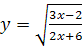 .
.
Решение. 1) Здесь на x не накладывается никаких ограничений, поэтому функция 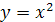 определяется на множестве
определяется на множестве 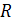 .
.
2) Если x =0, то y не имеет числового значения (на ноль делить нельзя). Для всех значений (кроме нуля) y принимает действительные значения, поэтому областью определения служит вся числовая ось, кроме x =0.
3) Функция определена для всех значений x, кроме тех, при которых знаменатель дроби обращается в ноль. Решив уравнение 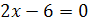 , найдем его корень
, найдем его корень 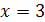 . Таким образом, область определения
. Таким образом, область определения 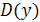 есть вся числовая ось, кроме точки
есть вся числовая ось, кроме точки 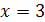 .
.
4) Функция определена для всех значений х, кроме тех, при которых знаменатель дроби обращается в ноль. Решив уравнение 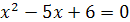 , найдем его корни
, найдем его корни 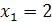 и
и 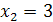 . Следовательно, область определения
. Следовательно, область определения 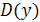 – вся числовая ось, кроме точек
– вся числовая ось, кроме точек 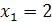 и
и 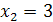 .
.
5) Квадратные корни определены для неотрицательных чисел. Поэтому функция  определена для всех значений x, удовлетворяющих неравенству
определена для всех значений x, удовлетворяющих неравенству 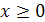 , т.е.
, т.е. 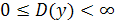 .
.
8) Функция определена для всех значений х, удовлетворяющих неравенству 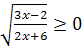 .
.
Таким образом, 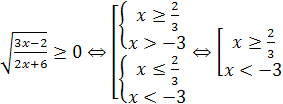 . Следовательно, областью определения функции является совокупность промежутков:
. Следовательно, областью определения функции является совокупность промежутков: 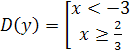 .
.
Пример 3. Постройте график функции 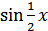
Решение. Область определения функции – вся числовая прямая. Множество значений 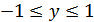 .
.
Функция нечетная, периодическая. Период данной функции найдем из равенства 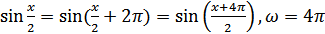 . Следовательно, сначала достаточно построить часть графика на отрезке
. Следовательно, сначала достаточно построить часть графика на отрезке  .
.
Найдем точки пересечения графика с осью 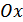 . Если
. Если  , то
, то 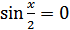 , откуда
, откуда 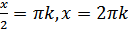 , где
, где 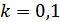 , т.е. на данном полупериоде кривая пересекает ось
, т.е. на данном полупериоде кривая пересекает ось 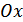 в двух точках
в двух точках 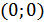 и
и 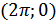 .
.
Максимум функции равен 1 при 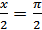 , т.е. при
, т.е. при 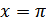 .
.
По этим данным построим график функции 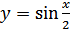 . Сначала график строим для положительного полупериода
. Сначала график строим для положительного полупериода  (рис. 27.8), затем на отрезке, соответствующем отрицательному полупериоду
(рис. 27.8), затем на отрезке, соответствующем отрицательному полупериоду 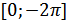 , и, наконец, на всей области определения (штриховая линия).
, и, наконец, на всей области определения (штриховая линия).

Рисунок 27.8 – график функции 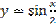
Пример 4. Постройте график функции 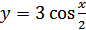 .
.
Решение. Мы знаем, как построить график функции 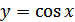 (на рис. 27.9 он изображен штриховой линией). Растягивая график функции
(на рис. 27.9 он изображен штриховой линией). Растягивая график функции 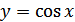 вдоль оси абсцисс в 2 раза, получим график функции
вдоль оси абсцисс в 2 раза, получим график функции 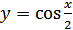 .
.
Затем полученный график растягиваем еще раз, но теперь по оси ординат в 3 раза, получим график функции 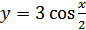 .
.
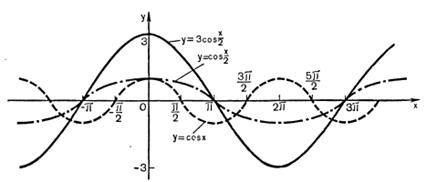
Рисунок 27.9 – график функции 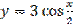
Пример 5. Постройте график функции: 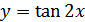
Решение. 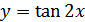 .
.
а) область определения – 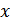 – любое число, кроме
– любое число, кроме 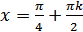 , где
, где 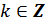 , так как
, так как 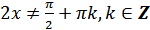 ;
;
б) область значений – вся числовая прямая, т.е. 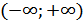 ;
;
в) функция не является ограниченной;
г) функция не принимает экстремальных значений;
д) функция периодическая, главный период 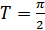 , так как
, так как 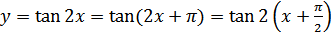 ;
;
е) функция не является монотонной на всей области определения, но функция возрастает на каждом из промежутков, 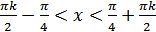 , где
, где 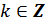 ;
;
точки пересечения с осями координат – точки 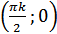 , где
, где 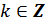 , так как
, так как 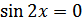 при
при 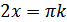 , т.е.
, т.е. 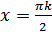 .
.
Учитывая периодичность, построим график функции 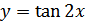 .
.
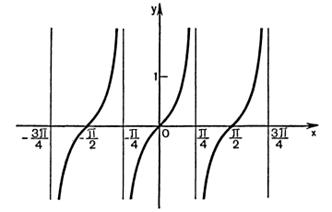
Рисунок 27.10 – график функции 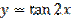
Пример 6. Постройте график функции: 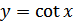 , используя формулу приведения.
, используя формулу приведения.
Решение. По формуле приведения 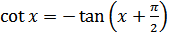 . Поэтому график функции
. Поэтому график функции 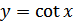 можно получить из графика функции
можно получить из графика функции 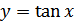 с помощью параллельного переноса влево на
с помощью параллельного переноса влево на  (рис. 27.11) и симметрией относительно оси абсцисс. График функции
(рис. 27.11) и симметрией относительно оси абсцисс. График функции 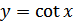 изображен на рис. 27.12.
изображен на рис. 27.12.
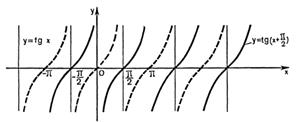 Рисунок 27.11 – график функции
Рисунок 27.11 – график функции 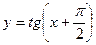
| 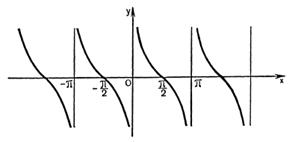 Рисунок 27.12 – график функции
Рисунок 27.12 – график функции 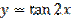
|
Задания к практической работе
Задание 1. Дана функция 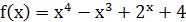 . Найдите
. Найдите 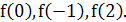
Задание 2. Дана функция 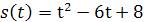 . Найдите
. Найдите 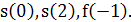
Задание 3. Дана функция 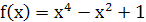 . Покажите, что
. Покажите, что 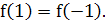
Задание 4. Дана функция 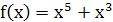 . Покажите, что
. Покажите, что 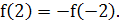
Задание 5. Найдите область определения функций:
1. 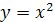 ;
;
2. 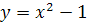 ;
;
3. 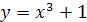
4. 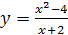 ;
;
5. 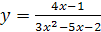 ;
;
6. 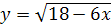 ;
;
7. 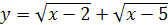 ;
;
8. 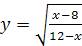 .
.
Задание 6. Дана функция 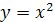 . Постройте графики функций:
. Постройте графики функций:
1. 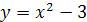 ;
;
2. 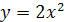 ;
;
3. 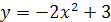 ;
;
4. 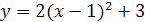 .
.
Задание 7. Дана функция 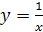 . Постройте графики функций:
. Постройте графики функций:
1) 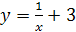 ;
;
2) 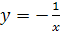 ;
;
3) 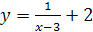 ;
;
4) 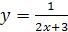 .
.
Задание 8. Постройте график функции:
1. 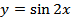 ;
;
2. 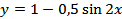 ;
;
3. 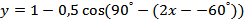 ;
;
4. 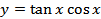 ;
;
5. 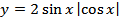 ;
;
6. 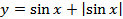 .
.
Задание 9. Постройте график функции:
1. 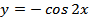 ;
;
2. 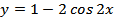 ;
;
3. 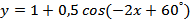 ;
;
4. 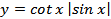 ;
;
5. 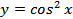 ;
;
6. 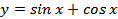 .
.
Задание 10. Постройте график функции:
1. 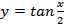 ;
;
2. 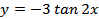 ;
;
3. 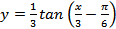 ;
;
4. 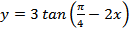 ;
;
5. 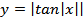 ;
;
6. 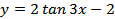 .
.
Задание 11. Постройте график функции:
1. 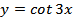 ; ;
| 2. 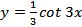 ; ;
|
3. 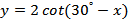 ; ;
| 4. 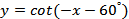 ; ;
|
5. 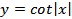 ; ;
| 6. 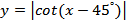 . .
|
Контрольные вопросы
1. Что называется функцией?
2. Какие способы задания функции существуют?
3. Перечислите основные свойства функций?
4. Что называется графиком функции?
5. Какие функции называются четными, а какие нечетными?
6. Перечислите основные свойства синуса.
7. Перечислите основные свойства косинуса.
8. Перечислите основные свойства тангенса.
9. Перечислите основные свойства котангенса.
Рекомендуемая литература: 1.1, 1.3, 1.4.
Практическая работа №28
Дата: 2018-12-28, просмотров: 387.