Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Цель: формирование навыков вычислений арксинуса, арккосинуса, арктангенса, арккотангенса чисел.

Вид работы: индивидуальный.

Время выполнения: 2 часа.

Теоретические сведения

1. Функция 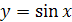 на отрезке  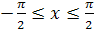имеет обратную функцию, которая называется арксинусом и обозначается .

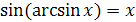, где ; .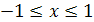

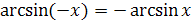Функция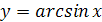

Перечислим основные свойства функции .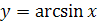

1) Область определения – отрезок .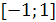

2) Множество значений – отрезок .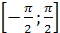

3) Функция 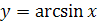 возрастает.

4) Функция 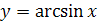 является нечетной, так как .

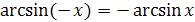График функции 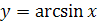 симметричен графику функции 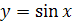,  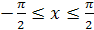относительно прямой  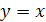(рис. 28.1).

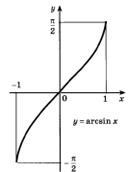
Рисунок 28.1 – график функции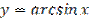

 

2. Функция 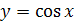 на отрезке  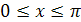имеет обратную функцию, которая называется арккосинусом и обозначается .

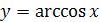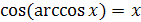, где ; .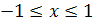

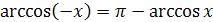Функция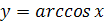

Перечислим основные свойства функции .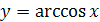

1) Область определения – отрезок .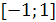

2) Множество значений – отрезок .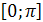

3) Функция 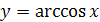 убывает.

График функции 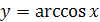 симметричен графику функции 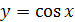,  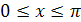относительно прямой  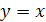(рис. 28.2).

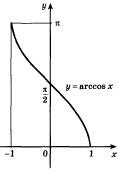
Рисунок 28.2 – график функции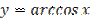

 

3. Функция 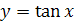 на промежутке  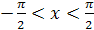имеет обратную функцию, которая называется арктангенсом и обозначается .

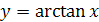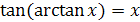, где .

.

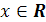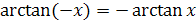Функция 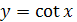на промежутке  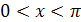имеет обратную функцию, которая называется арккотангенсом и обозначается .

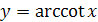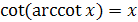, где ; .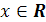

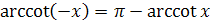Функция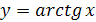

Перечислим основные свойства функции .

1) Область определения – множество 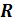 всех действительных чисел.

2) Множество значений – интервал .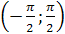

3) Функция  возрастает.

4) Функция  является нечетной: .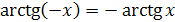

График функции  получается из графика функции 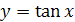, , 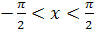симметрией относительно прямой  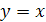(рис. 28.3).

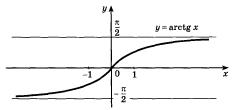
Рисунок 28.3 – график функции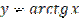

 

Пример 1. Проверьте, справедливы ли равенства:

1. ;

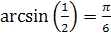2. ;

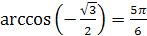3. .

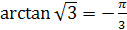Решение: 1. 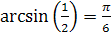, так как  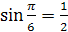 и .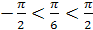

2. 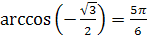, так как  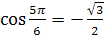и .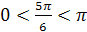

3. 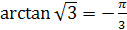, так как  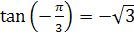и .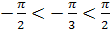

Пример 2. Найдите область определения функции .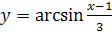

Решение. Так как функция 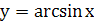 определена при 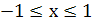, то функция  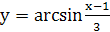определена для тех значений 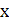, для которых выполняются неравенства 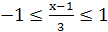. Отсюда , .

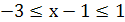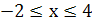Пример 3. Решите уравнение .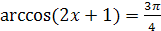

Решение. Так как 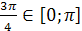, то по определению арккосинуса числа данное уравнение равносильно уравнению 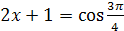, откуда , .

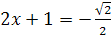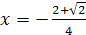Задания к практической работе

Задание 1. Проверьте, справедливы ли равенства:

1. ;

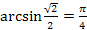2. ;

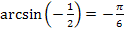3. ;

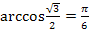4. ;

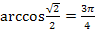5. ;

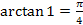6. ;

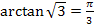7. ;

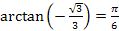8. .

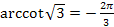Задание 2. Вычислите:

1. ;

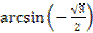2. ;

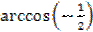3. ;

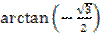4. ;

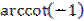5. .

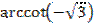Задание 3. Докажите справедливость неравенств:

1. ;

2. ;

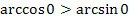3. ;

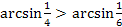4.

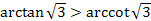
Задание 4. Вычислите:

1. 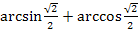;	2. ;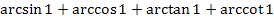
3. 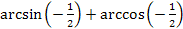;	4. ;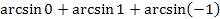
5. 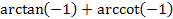;	6. ;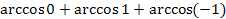
7. .

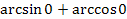Задание 5. Найдите область определения функции:

1. ;

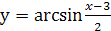2. ;

 

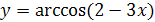3. ;

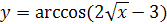4. .

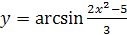Задание 6. Докажите, что график функции 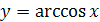 симметричен относительно точки .

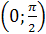Задание 7. Решите уравнение:

1. 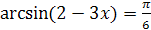;	2. ;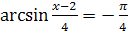
3. 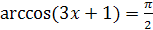;	4. ;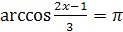
5. 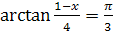;	6. .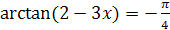

Контрольные вопросы

1. Что называется арксинусом?

2. Что называется арккосинусом?

3. Что называется арктангенсом?

4. Что называется арккотангенсом?

5. Как вычислить арксинус, арккосинус, арктангенс и арккотангенс от отрицательного значения?

6. Перечислите основные свойства функции .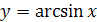

7. Перечислите основные свойства функции .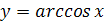

8. Перечислите основные свойства функции .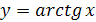

Рекомендуемая литература: 1.1, 1.4.

Практическая работа№29