ОУДп.01 МАТЕМАТИКА: АЛГЕБРА, НАЧАЛА
МАТЕМАТИЧЕСКОГО АНАЛИЗА, ГЕОМЕТРИЯ
Методические указания по выполнению практических работ
по дисциплине ОУДп.01 Математика: алгебра и начала
математического анализа, геометрия
для обучающихся по всем специальностям
очной формы обучения
(часть 4)
Составитель С.И. Москалевская,
Преподаватель высшей квалификационной категории
Тюмень
ТИУ
2018
ОУДп.01 Математика: алгебра, начала математического анализа, геометрия методические указания по выполнению практических работ по дисциплине ОУДп.01 Математика: алгебра, начала математического анализа, геометрия для обучающихся по всем специальностям очной формы обучения (часть 4) / сост. Москалевская С.И.; Тюменский индустриальный университет. – Тюмень: Издательский центр БИК, ТИУ, 2018. –32 с.
Ответственный редактор: Т.М. Белкина, председатель цикловой комиссии общеобразовательных дисциплин.
Методические указания рассмотрены и рекомендованы к изданию на заседании цикловой комиссии общеобразовательных дисциплин
«18» января 2018 года, протокол №1
Аннотация
Методические указания по дисциплине ОУДп.01 Математика: алгебра, начала математического анализа, геометрия предназначены для обучающихся по всем специальностям очной формы обучения.
Методические указания по дисциплине ОУДп.01 Математика: алгебра, начала математического анализа, геометрия составлены в соответствии с рабочей программой и состоят из содержания практических работ, пояснительной записки, общих требований по выполнению практических работ, критериев оценки выполнения и контрольных вопросов.
Методические указания могут оказать помощь преподавателям в организации самостоятельных работ, а также могут использоваться обучающимися при подготовке к занятиям и экзамену.
 | |
 |
Содержание
| Пояснительная записка | 4 |
| Общие требования к выполнению и оформлению практических работ | 4 |
| Критерии оценки практических работ | 5 |
| Практическая работа № 27 Исследование функции. Свойства линейной, квадратичной, кусочно-линейной функций. Непрерывные и периодические функции. Свойства и графики синуса, косинуса и котангенса. | 5 |
| Практическая работа № 28 Обратные тригонометрические функции | 13 |
| Практическая работа № 29 Корни уравнений. Равносильность уравнений | 17 |
| Практическая работа № 30 Основные приемы решения уравнений | 19 |
| Практическая работа № 31 Решение систем уравнений | 24 |
| Практическая работа № 32 Показательные, логарифмические уравнения | 26 |
| Список литературы | 31 |
Пояснительная записка
Методические указания по выполнению практических работ составлены в соответствии с рабочей программой по дисциплине ОУДп.01 Математика: алгебра, начала математического анализа, геометрия на базе основного общего образования.
Практические работы занимают важное место при изучении дисциплины ОУДп.01 Математика: алгебра и начала математического анализа, геометрия. Цель изучения дисциплины состоит в формировании знаний, практических умений и навыков решения элементарных математических задач.
В результате выполнения практических работ обучающийся должен:
иметь представление:
- о месте и роли математики в современном мире, общности ее понятий и представлений;
- о логическом строении дисциплины;
- о междисциплинарной связи математики со специальными дисциплинами;
знать и уметь:
- теоретические разделы каждой темы;
уметь:
- решать примеры и задачи по каждой теме.
Методические указания по выполнению практических работ состоят из пояснительной записки, критериев оценки работы, общих требований к выполнению и оформлению практических занятий, содержания практических занятий, которые снабжены основными теоретическими положениями, заданиями, контрольными вопросами и списком литературы.
На выполнение каждой работы отводится определенное количество часов в соответствии с тематическим планом.
Форма отчетности указана для каждого практического занятия.
Методические указания по выполнению практических работ окажут помощь преподавателям в организации и управлении работой обучающихся в процессе занятий, а обучающиеся могут использовать их как пособие для повторения изученного материала, подготовке к экзамену.
ОБЩИЕ ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКИХ РАБОТ
Практические задания должны оформляться в отдельной тетради и содержать:
- тему, цель, вид работы, время выполнения практического задания;
- условия заданий;
- необходимые расчетные формулы, понятия;
- подробные решения заданий;
- для успешной защиты отчета по практическим заданиям обучающийся должен правильно ответить на рекомендуемые контрольные вопросы, проявить навыки решения задач и умение иллюстрировать теоретический материал расчетами для выполненных заданий.
- отчет должен заключаться выводом о практической работе.
Практическая работа №27
Теоретические сведения
Переменная y называется функцией переменной x, если каждому допустимому значению x соответствует определенное значение y.
Символически функциональная зависимость между переменной y (функцией) и переменной x (аргументом) записывается с помощью равенства y = f ( x ), где f обозначает совокупность действий, которые надо произвести над x, чтобы получить y.
Областью определения функции D ( y ) называется множество всех действительных значений аргумента x (множество всех точек числовой оси), при которых она имеет действительное значение.
Множеством значений функции E ( y ) называется множество всех действительных значений функции y, которые она может принимать.
Функция может быть задана аналитически (формулой), таблицей, графиком или каким-либо другим способом.
Функцию y = f ( x ) иногда можно представить таблицей, в первой строке которой перечисляются значения независимой переменной x, а во второй – соответствующие значения f ( x ) зависимой переменной.
Графиком функции y = f ( x ) называется множество всех точек координатной плоскости с координатами ( x ; f ( x )).
Известны графики многих функций. Например, график функции y = kx + b есть прямая линия (рис. 27.1), график функции y = x 2 – парабола (рис. 27.2), график функции 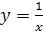 (обратная пропорциональная зависимость) – гипербола (рис. 27.3).
(обратная пропорциональная зависимость) – гипербола (рис. 27.3).
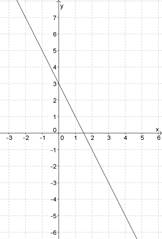 Рисунок 27.1 – график функции
y= kx+ b ( k<0)
Рисунок 27.1 – график функции
y= kx+ b ( k<0)
|
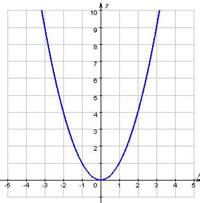 Рисунок 27.2 –
график функции y= x2
Рисунок 27.2 –
график функции y= x2
|
 Рисунок 27.3 – график функции
Рисунок 27.3 – график функции 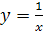
|
В графике содержится вся информация о функции.
Функция f (х) называется возрастающей на данном числовом промежутке Х, если большему значению аргумента 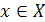 соответствует большее значение функции
соответствует большее значение функции 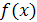 , т. е. для любых
, т. е. для любых 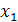 и
и 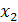 из промежутка X, таких, что
из промежутка X, таких, что 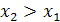 , выполнено неравенство
, выполнено неравенство 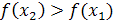 .
.
Функция f (х) называется убывающей на данном числовом промежутке X, если большему значению аргумента 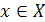 соответствует меньшее значение функции f (х), т. е. для любых
соответствует меньшее значение функции f (х), т. е. для любых 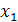 и
и 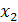 из промежутка X, таких, что
из промежутка X, таких, что 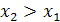 , выполнено неравенство
, выполнено неравенство 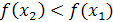 .
.
Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.
Функция y = f(x) называется четной, если она обладает следующими двумя свойствами:
1) область определения этой функции симметрична относительно точки О (т. е. если точка а принадлежит области определения, то точка - а также принадлежит области определения);
2) для любого значения х, принадлежащего области определения этой функции, выполняется равенство 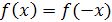 .
.
Функция y = f(x) называется нечетной, если:
1) область определения этой функции симметрична относительно точки О;
2) для любого значения 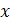 , принадлежащего области определения этой функции, выполняется равенство
, принадлежащего области определения этой функции, выполняется равенство 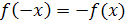 .
.
Функция f называется периодической, если существует такое число 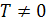 , что при любом х из области определения функции числа
, что при любом х из области определения функции числа 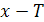 и
и 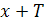 также принадлежат этой области и выполняется равенство
также принадлежат этой области и выполняется равенство 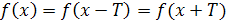 . В этом случае число Т называется периодом функции f.
. В этом случае число Т называется периодом функции f.
Если 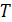 - период функции, то
- период функции, то 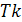 , где
, где 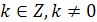 , также период функции. Следовательно, всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.
, также период функции. Следовательно, всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.
Функция 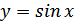
Основные свойства функции 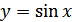 :
:
а) область определения – множество всех действительных чисел;
б) множество значений – отрезок 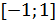 , значит, синус – функция ограниченная;
, значит, синус – функция ограниченная;
в) функция нечетная: 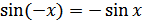 для всех
для всех 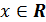 ;
;
г) функция периодическая с наименьшим положительным периодом 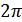 , т.е.
, т.е. 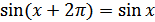 для всех
для всех 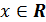 ;
;
д) 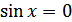 при
при 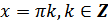 ;
;
е) 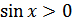 для всех
для всех 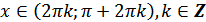 ;
;
ж) 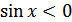 для всех
для всех 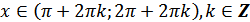 ;
;
з) функция возрастает от -1 до 1 на промежутках 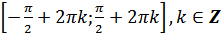 ;
;
и) функция убывает от 1 до -1 на промежутках 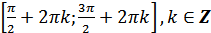 ;
;
к) функция принимает наибольшее значение, равное 1, в точках 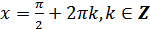 ;
;
л) функция принимает наименьшее значение, равное -1, в точках 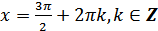 .
.
График функции 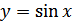 изображен на рисунке 27.4. Кривая, являющаяся графиком функции
изображен на рисунке 27.4. Кривая, являющаяся графиком функции 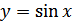 , называется синусоидой.
, называется синусоидой.
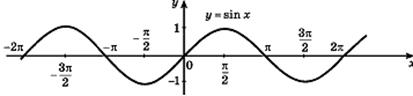
Рисунок 27.4 – график функции 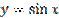
Функция 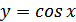
Основные свойства функции 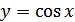 :
:
а) область определения – множество всех действительных чисел;
б) множество значений – отрезок 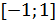 , значит, косинус – функция ограниченная;
, значит, косинус – функция ограниченная;
в) функция четная: 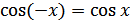 для всех
для всех 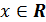 ;
;
г) функция периодическая с наименьшим положительным периодом 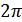 , т.е.
, т.е. 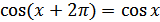 для всех
для всех 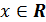 ;
;
д) 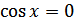 при
при 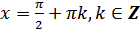 ;
;
е) 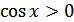 для всех
для всех 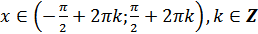 ;
;
ж) 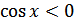 для всех
для всех 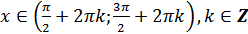 ;
;
з) функция убывает от -1 до 1 на промежутках 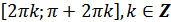 ;
;
и) функция возрастает от 1 до -1 на промежутках 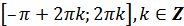 ;
;
к) функция принимает наибольшее значение, равное 1, в точках 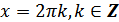 ;
;
л) функция принимает наименьшее значение, равное -1, в точках 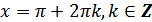 .
.
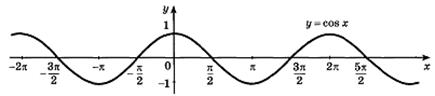
Рисунок 27.5 – график функции 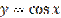
Функция 
Основные свойства функции 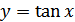 :
:
а) область определения – множество всех действительных чисел, кроме чисел вида 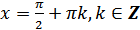 ;
;
б) множество значений – вся числовая прямая, таким образом, тангенс – функция неограниченная;
в) функция нечетная: 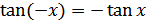 для всех
для всех 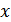 из области определения;
из области определения;
г) функция периодическая с наименьшим положительным периодом 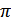 , т.е.
, т.е. 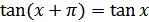 для всех
для всех 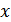 из области определения;
из области определения;
д) 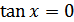 при
при 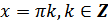 ;
;
е) 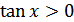 для всех
для всех 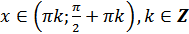 ;
;
ж) 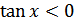 для всех
для всех 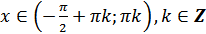 ;
;
з) функция возрастает на промежутках 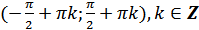 .
.
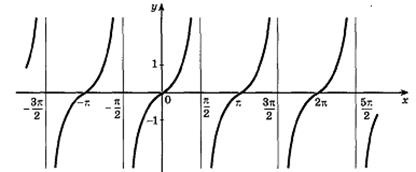
Рисунок 27.6 – график функции 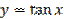
Функция 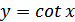
Основные свойства функции 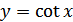 :
:
а) область определения – множество всех действительных чисел, кроме чисел вида 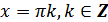 ;
;
б) множество значений – вся числовая прямая, таким образом, котангенс – функция неограниченная;
в) функция нечетная: 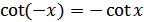 для всех
для всех 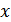 из области определения;
из области определения;
г) функция периодическая с наименьшим положительным периодом 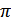 , т.е.
, т.е.  для всех
для всех 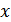 из области определения;
из области определения;
д)  при
при 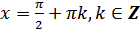 ;
;
е) 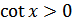 для всех
для всех 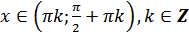 ;
;
ж) 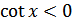 для всех
для всех 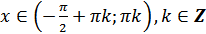 ;
;
з) функция убывает на каждом из промежутков 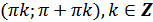 .
.
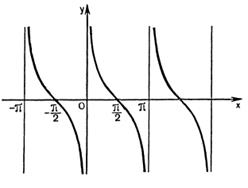
Рисунок 27.7 – график функции 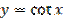
Пример 1. Дана функция 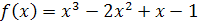 .
.
Найдите 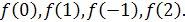
Решение. Чтобы вычислить значение 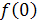 , необходимо в данную функцию вместо аргумента x подставить его значение
, необходимо в данную функцию вместо аргумента x подставить его значение  . Имеем
. Имеем 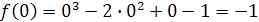 .
.
Аналогично получим 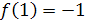 ,
, 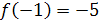 и
и 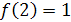 .
.
Пример 2. Найдите область определения функции:
1) 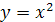 ;
;
2) 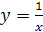 ;
;
3) 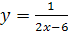 ;
;
4) 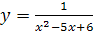 ;
;
5)  ;
;
6) 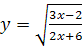 .
.
Решение. 1) Здесь на x не накладывается никаких ограничений, поэтому функция 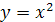 определяется на множестве
определяется на множестве 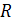 .
.
2) Если x =0, то y не имеет числового значения (на ноль делить нельзя). Для всех значений (кроме нуля) y принимает действительные значения, поэтому областью определения служит вся числовая ось, кроме x =0.
3) Функция определена для всех значений x, кроме тех, при которых знаменатель дроби обращается в ноль. Решив уравнение 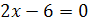 , найдем его корень
, найдем его корень 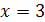 . Таким образом, область определения
. Таким образом, область определения 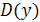 есть вся числовая ось, кроме точки
есть вся числовая ось, кроме точки 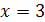 .
.
4) Функция определена для всех значений х, кроме тех, при которых знаменатель дроби обращается в ноль. Решив уравнение 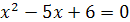 , найдем его корни
, найдем его корни 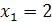 и
и 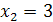 . Следовательно, область определения
. Следовательно, область определения 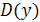 – вся числовая ось, кроме точек
– вся числовая ось, кроме точек 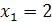 и
и 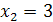 .
.
5) Квадратные корни определены для неотрицательных чисел. Поэтому функция  определена для всех значений x, удовлетворяющих неравенству
определена для всех значений x, удовлетворяющих неравенству 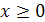 , т.е.
, т.е. 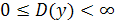 .
.
8) Функция определена для всех значений х, удовлетворяющих неравенству 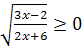 .
.
Таким образом, 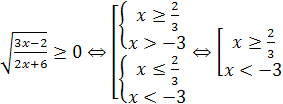 . Следовательно, областью определения функции является совокупность промежутков:
. Следовательно, областью определения функции является совокупность промежутков: 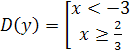 .
.
Пример 3. Постройте график функции 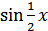
Решение. Область определения функции – вся числовая прямая. Множество значений 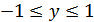 .
.
Функция нечетная, периодическая. Период данной функции найдем из равенства 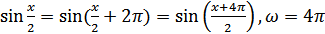 . Следовательно, сначала достаточно построить часть графика на отрезке
. Следовательно, сначала достаточно построить часть графика на отрезке  .
.
Найдем точки пересечения графика с осью 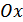 . Если
. Если  , то
, то 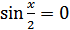 , откуда
, откуда 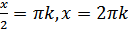 , где
, где 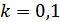 , т.е. на данном полупериоде кривая пересекает ось
, т.е. на данном полупериоде кривая пересекает ось 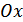 в двух точках
в двух точках 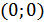 и
и 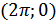 .
.
Максимум функции равен 1 при 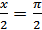 , т.е. при
, т.е. при 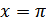 .
.
По этим данным построим график функции 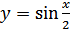 . Сначала график строим для положительного полупериода
. Сначала график строим для положительного полупериода  (рис. 27.8), затем на отрезке, соответствующем отрицательному полупериоду
(рис. 27.8), затем на отрезке, соответствующем отрицательному полупериоду 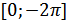 , и, наконец, на всей области определения (штриховая линия).
, и, наконец, на всей области определения (штриховая линия).

Рисунок 27.8 – график функции 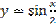
Пример 4. Постройте график функции 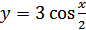 .
.
Решение. Мы знаем, как построить график функции 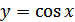 (на рис. 27.9 он изображен штриховой линией). Растягивая график функции
(на рис. 27.9 он изображен штриховой линией). Растягивая график функции 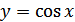 вдоль оси абсцисс в 2 раза, получим график функции
вдоль оси абсцисс в 2 раза, получим график функции 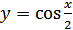 .
.
Затем полученный график растягиваем еще раз, но теперь по оси ординат в 3 раза, получим график функции 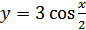 .
.
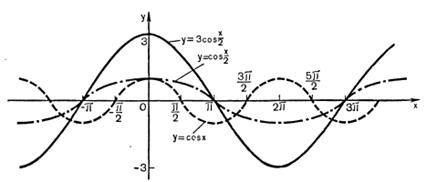
Рисунок 27.9 – график функции 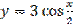
Пример 5. Постройте график функции: 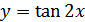
Решение. 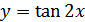 .
.
а) область определения – 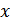 – любое число, кроме
– любое число, кроме 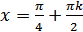 , где
, где 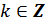 , так как
, так как 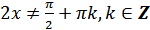 ;
;
б) область значений – вся числовая прямая, т.е. 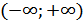 ;
;
в) функция не является ограниченной;
г) функция не принимает экстремальных значений;
д) функция периодическая, главный период 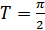 , так как
, так как 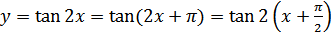 ;
;
е) функция не является монотонной на всей области определения, но функция возрастает на каждом из промежутков, 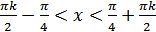 , где
, где 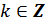 ;
;
точки пересечения с осями координат – точки 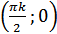 , где
, где 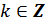 , так как
, так как 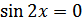 при
при 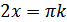 , т.е.
, т.е. 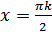 .
.
Учитывая периодичность, построим график функции 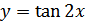 .
.
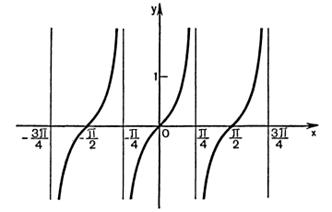
Рисунок 27.10 – график функции 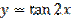
Пример 6. Постройте график функции: 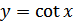 , используя формулу приведения.
, используя формулу приведения.
Решение. По формуле приведения 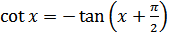 . Поэтому график функции
. Поэтому график функции 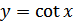 можно получить из графика функции
можно получить из графика функции 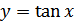 с помощью параллельного переноса влево на
с помощью параллельного переноса влево на  (рис. 27.11) и симметрией относительно оси абсцисс. График функции
(рис. 27.11) и симметрией относительно оси абсцисс. График функции 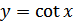 изображен на рис. 27.12.
изображен на рис. 27.12.
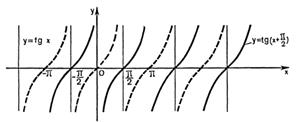 Рисунок 27.11 – график функции
Рисунок 27.11 – график функции 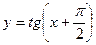
| 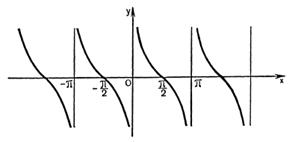 Рисунок 27.12 – график функции
Рисунок 27.12 – график функции 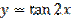
|
Задания к практической работе
Задание 1. Дана функция 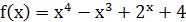 . Найдите
. Найдите 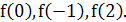
Задание 2. Дана функция 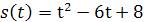 . Найдите
. Найдите 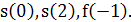
Задание 3. Дана функция 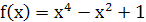 . Покажите, что
. Покажите, что 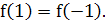
Задание 4. Дана функция 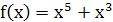 . Покажите, что
. Покажите, что 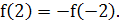
Задание 5. Найдите область определения функций:
1. 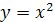 ;
;
2. 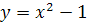 ;
;
3. 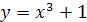
4. 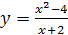 ;
;
5. 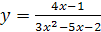 ;
;
6. 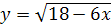 ;
;
7. 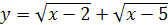 ;
;
8. 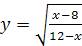 .
.
Задание 6. Дана функция 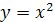 . Постройте графики функций:
. Постройте графики функций:
1. 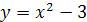 ;
;
2. 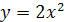 ;
;
3. 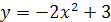 ;
;
4. 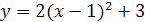 .
.
Задание 7. Дана функция 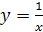 . Постройте графики функций:
. Постройте графики функций:
1) 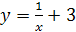 ;
;
2) 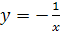 ;
;
3) 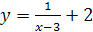 ;
;
4) 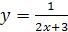 .
.
Задание 8. Постройте график функции:
1. 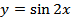 ;
;
2. 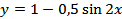 ;
;
3. 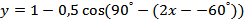 ;
;
4. 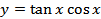 ;
;
5. 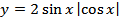 ;
;
6. 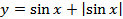 .
.
Задание 9. Постройте график функции:
1. 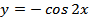 ;
;
2. 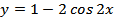 ;
;
3. 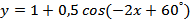 ;
;
4. 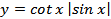 ;
;
5. 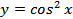 ;
;
6. 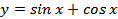 .
.
Задание 10. Постройте график функции:
1. 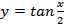 ;
;
2. 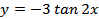 ;
;
3. 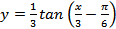 ;
;
4. 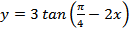 ;
;
5. 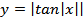 ;
;
6. 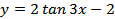 .
.
Задание 11. Постройте график функции:
1. 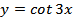 ; ;
| 2. 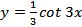 ; ;
|
3. 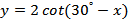 ; ;
| 4. 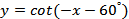 ; ;
|
5. 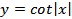 ; ;
| 6. 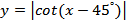 . .
|
Контрольные вопросы
1. Что называется функцией?
2. Какие способы задания функции существуют?
3. Перечислите основные свойства функций?
4. Что называется графиком функции?
5. Какие функции называются четными, а какие нечетными?
6. Перечислите основные свойства синуса.
7. Перечислите основные свойства косинуса.
8. Перечислите основные свойства тангенса.
9. Перечислите основные свойства котангенса.
Рекомендуемая литература: 1.1, 1.3, 1.4.
Практическая работа №28
Теоретические сведения
1. Функция 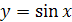 на отрезке
на отрезке 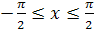 имеет обратную функцию, которая называется арксинусом и обозначается
имеет обратную функцию, которая называется арксинусом и обозначается  .
.
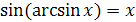 , где
, где 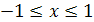 ;
; 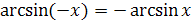 .
.
Функция 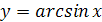
Перечислим основные свойства функции 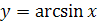 .
.
1) Область определения – отрезок 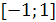 .
.
2) Множество значений – отрезок 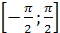 .
.
3) Функция 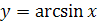 возрастает.
возрастает.
4) Функция 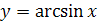 является нечетной, так как
является нечетной, так как 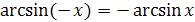 .
.
График функции 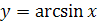 симметричен графику функции
симметричен графику функции 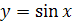 ,
, 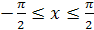 относительно прямой
относительно прямой 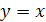 (рис. 28.1).
(рис. 28.1).
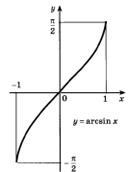
Рисунок 28.1 – график функции 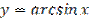
2. Функция 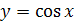 на отрезке
на отрезке 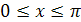 имеет обратную функцию, которая называется арккосинусом и обозначается
имеет обратную функцию, которая называется арккосинусом и обозначается 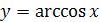 .
.
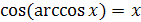 , где
, где 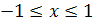 ;
; 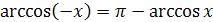 .
.
Функция 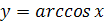
Перечислим основные свойства функции 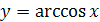 .
.
1) Область определения – отрезок 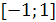 .
.
2) Множество значений – отрезок 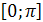 .
.
3) Функция 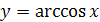 убывает.
убывает.
График функции 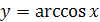 симметричен графику функции
симметричен графику функции 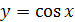 ,
, 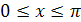 относительно прямой
относительно прямой 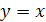 (рис. 28.2).
(рис. 28.2).
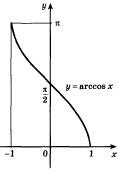
Рисунок 28.2 – график функции 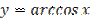
3. Функция 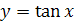 на промежутке
на промежутке 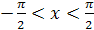 имеет обратную функцию, которая называется арктангенсом и обозначается
имеет обратную функцию, которая называется арктангенсом и обозначается 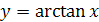 .
.
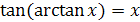 , где
, где 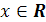 .
.
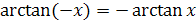 .
.
Функция 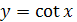 на промежутке
на промежутке 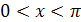 имеет обратную функцию, которая называется арккотангенсом и обозначается
имеет обратную функцию, которая называется арккотангенсом и обозначается 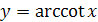 .
.
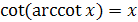 , где
, где 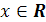 ;
; 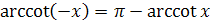 .
.
Функция 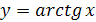
Перечислим основные свойства функции  .
.
1) Область определения – множество 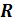 всех действительных чисел.
всех действительных чисел.
2) Множество значений – интервал 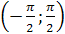 .
.
3) Функция  возрастает.
возрастает.
4) Функция  является нечетной:
является нечетной: 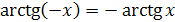 .
.
График функции  получается из графика функции
получается из графика функции 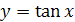 ,
, 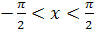 , симметрией относительно прямой
, симметрией относительно прямой 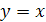 (рис. 28.3).
(рис. 28.3).
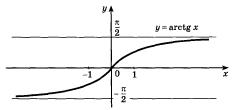
Рисунок 28.3 – график функции 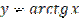
Пример 1. Проверьте, справедливы ли равенства:
1. 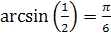 ;
;
2. 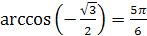 ;
;
3. 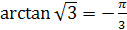 .
.
Решение: 1. 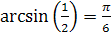 , так как
, так как 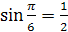 и
и 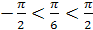 .
.
2. 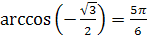 , так как
, так как 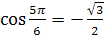 и
и 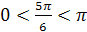 .
.
3. 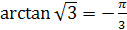 , так как
, так как 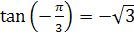 и
и 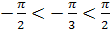 .
.
Пример 2. Найдите область определения функции 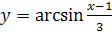 .
.
Решение. Так как функция 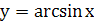 определена при
определена при 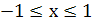 , то функция
, то функция 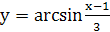 определена для тех значений
определена для тех значений 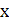 , для которых выполняются неравенства
, для которых выполняются неравенства 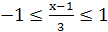 . Отсюда
. Отсюда 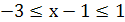 ,
, 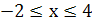 .
.
Пример 3. Решите уравнение 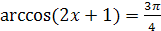 .
.
Решение. Так как 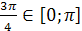 , то по определению арккосинуса числа данное уравнение равносильно уравнению
, то по определению арккосинуса числа данное уравнение равносильно уравнению 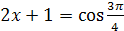 , откуда
, откуда 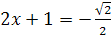 ,
, 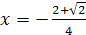 .
.
Задания к практической работе
Задание 1. Проверьте, справедливы ли равенства:
1. 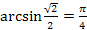 ;
;
2. 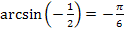 ;
;
3. 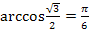 ;
;
4. 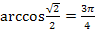 ;
;
5. 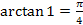 ;
;
6. 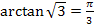 ;
;
7. 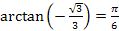 ;
;
8. 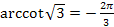 .
.
Задание 2. Вычислите:
1. 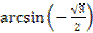 ;
;
2. 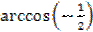 ;
;
3. 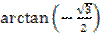 ;
;
4. 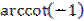 ;
;
5. 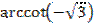 .
.
Задание 3. Докажите справедливость неравенств:
1.  ;
;
2. 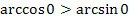 ;
;
3. 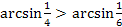 ;
;
4. 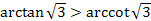
Задание 4. Вычислите:
1. 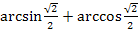 ; ;
| 2. 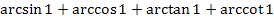 ; ;
|
3. 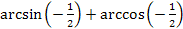 ; ;
| 4. 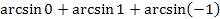 ; ;
|
5. 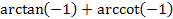 ; ;
| 6. 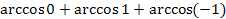 ; ;
|
7. 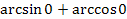 . .
|
Задание 5. Найдите область определения функции:
1. 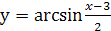 ;
;
2. 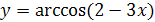 ;
;
3. 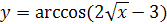 ;
;
4. 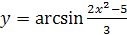 .
.
Задание 6. Докажите, что график функции 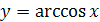 симметричен относительно точки
симметричен относительно точки 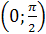 .
.
Задание 7. Решите уравнение:
1. 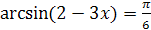 ; ;
| 2. 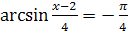 ; ;
|
3. 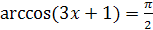 ; ;
| 4. 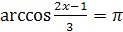 ; ;
|
5. 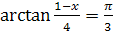 ; ;
| 6. 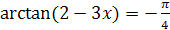 . .
|
Контрольные вопросы
1. Что называется арксинусом?
2. Что называется арккосинусом?
3. Что называется арктангенсом?
4. Что называется арккотангенсом?
5. Как вычислить арксинус, арккосинус, арктангенс и арккотангенс от отрицательного значения?
6. Перечислите основные свойства функции 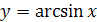 .
.
7. Перечислите основные свойства функции 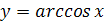 .
.
8. Перечислите основные свойства функции 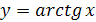 .
.
Рекомендуемая литература: 1.1, 1.4.
Практическая работа№29
Теоретические сведения
Уравнения, имеющие одно и то же множество корней, называются равносильными.
Уравнения, не имеющие корней, также являются равносильными.
Например, уравнения 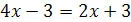 и
и 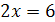 равносильны, так как каждое из них имеет только один корень
равносильны, так как каждое из них имеет только один корень 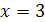 . Уравнения
. Уравнения 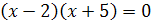 и
и 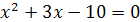 также равносильны, так как они имеют одни и те же корни
также равносильны, так как они имеют одни и те же корни 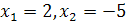 . Уравнения
. Уравнения 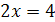 и
и 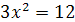 не равносильны, так как первое имеет корень
не равносильны, так как первое имеет корень 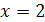 , а второе – корни
, а второе – корни 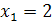 и
и 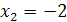 .
.
Два уравнения равносильны, если каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого уравнения.
Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.
Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.
При этих преобразованиях исходное уравнение заменяется на равносильное ему уравнение.
Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называют следствием первого уравнения. Иначе, если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения.
Из этого определения и определения равносильности уравнений следует, что:
1) если два уравнения равносильны, то каждое из них является следствием другого;
2) если каждое из двух уравнений является следствием другого, то эти уравнения равносильны.
При решении уравнений главное – не потерять корни, а наличие посторонних корней можно установить проверкой.
Посторонние корни могут получиться при умножении обеих частей уравнения на выражение, содержащее неизвестное.
Потеря корней может произойти при делении обеих частей уравнения на выражение, содержащее неизвестное.
При решении уравнения можно делать только такие его преобразования, при которых не происходит потерь корней. Если при этом получаются уравнения – следствия данного, то необходима проверка найденных корней.
Пример 1. Решить уравнение 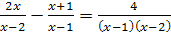 .
.
Решение. Умножив обе части уравнения на общий знаменатель всех трех дробей, т.е. на 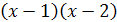 , получим
, получим 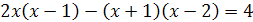 , откуда
, откуда 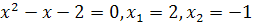 .
.
Проверка. 1) При 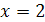 знаменатели двух дробей уравнения равны нулю. Поэтому
знаменатели двух дробей уравнения равны нулю. Поэтому 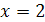 не является корнем данного уравнения.
не является корнем данного уравнения.
2) При 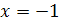 левая часть уравнения равна
левая часть уравнения равна 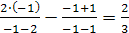 , правая часть равна
, правая часть равна 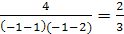 .
.
Таким образом, корнем уравнения является 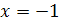 , а корень
, а корень 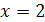 - корнем данного уравнения не является, его называют посторонним корнем.
- корнем данного уравнения не является, его называют посторонним корнем.
Пример 2. Решите уравнение 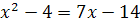 .
.
Решение. Преобразуем данное уравнение так:
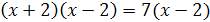 ,
,
Откуда 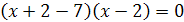 , т.е.
, т.е. 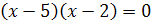 , следовательно,
, следовательно, 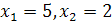 .
.
Задания к практической работе
Задание 1. Равносильны ли следующие уравнения:
1. 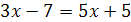 и
и 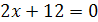 ;
;
2. 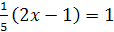 и
и 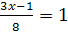 ;
;
3. 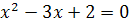 и
и 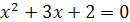 ;
;
4. 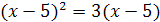 и
и 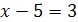 ;
;
5. 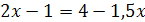 и
и  ;
;
6. 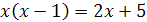 и
и 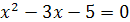 ;
;
7. 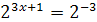 и
и 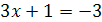 ;
;
8. 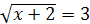 и
и 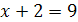 .
.
Задание 2. Решите уравнения:
1. 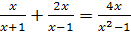 ; ;
| 2. 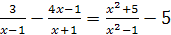 ; ;
|
3. 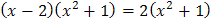 ; ;
| 4. 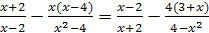 . .
|
Контрольные вопросы
1. Какие уравнения называются равносильными? Приведите примеры.
2. Какое уравнение называется следствием другого? Приведите примеры.
3. Какие методы преобразования уравнений вы знаете?
Рекомендуемая литература: 1.1, 1.3, 1.4, 2.1.
Практическая работа №30
Теоретические сведения
I. Уравнение 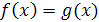 называется рациональным, если
называется рациональным, если 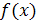 и
и 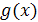 – рациональные выражения.
– рациональные выражения.
Чтобы решить рациональное уравнение, нужно:
1) найти общий знаменатель всех имеющихся дробей;
2) заменить данное уравнение целым, умножив обе его части на общий знаменатель;
3) решить полученное целое уравнение;
4) исключить из его корней те, которые обращают в нуль общий знаменатель.
Пример 1. Решите уравнение 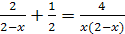 .
.
Решение. Общий знаменатель имеющихся дробей является 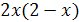 . Найдя дополнительные множители для каждой дроби, освободимся от знаменателей. Имеем:
. Найдя дополнительные множители для каждой дроби, освободимся от знаменателей. Имеем: 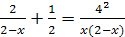 ;
;
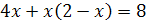
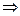
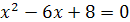 .
.
Из уравнения 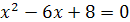 находим
находим 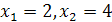 . Осталось проверить, обращают ли найденные корни в нуль выражение
. Осталось проверить, обращают ли найденные корни в нуль выражение 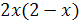 , т.е. проверить выполнение условия
, т.е. проверить выполнение условия 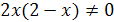 . Замечаем, что 2 не удовлетворяет этому условию, а 4 удовлетворяет. Значит,
. Замечаем, что 2 не удовлетворяет этому условию, а 4 удовлетворяет. Значит, 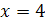 - единственный корень уравнения.
- единственный корень уравнения.
Решение уравнений 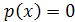 методом разложения его левой части на множители.
методом разложения его левой части на множители.
Суть этого метода состоит в том, что нужно решить уравнение 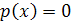 , где
, где 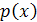 – многочлен степени
– многочлен степени 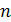 . Предположим, что нам удалось разложить многочлен на множители:
. Предположим, что нам удалось разложить многочлен на множители: 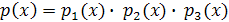 , где
, где 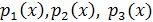 – многочлены более низкой степени, чем
– многочлены более низкой степени, чем 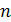 . Тогда уравнение
. Тогда уравнение 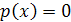 примет вид
примет вид 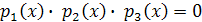 . Если
. Если 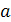 – корень уравнения
– корень уравнения 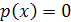 , то
, то 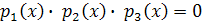 , а потому хотя бы одно из чисел
, а потому хотя бы одно из чисел 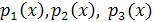 равно нулю. Значит
равно нулю. Значит 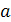 , - корень хотя бы одного из уравнений
, - корень хотя бы одного из уравнений
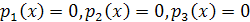 .
.
Итак, если 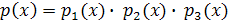 , где
, где 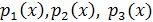 – многочлены, то вместо уравнения
– многочлены, то вместо уравнения 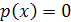 нужно решить совокупность уравнений
нужно решить совокупность уравнений 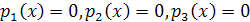 . Все найденные корни этих уравнений, и только они, будут корнями уравнения
. Все найденные корни этих уравнений, и только они, будут корнями уравнения 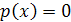 .
.
Пример 2. Решите уравнение 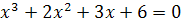 .
.
Решение. Разложим на множители левую часть уравнения. Имеем 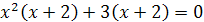 , откуда
, откуда 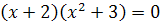 . Значит, либо
. Значит, либо 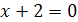 , либо
, либо 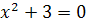 . Из первого уравнения находим
. Из первого уравнения находим 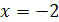 , второе уравнение корней не имеет. Таким образом, корень уравнения -2.
, второе уравнение корней не имеет. Таким образом, корень уравнения -2.
Решение уравнений методом введения новой переменной
Суть этого метода поясним на примере.
Пример 3. Решите уравнение 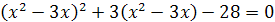 .
.
Решение. Положив 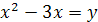 , получим уравнение
, получим уравнение 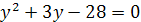 , откуда находим
, откуда находим 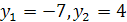 . Теперь задача сводится к решению совокупности уравнений:
. Теперь задача сводится к решению совокупности уравнений: 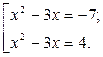
Первое квадратное уравнение не имеет действительных корней, так как его дискриминант отрицателен.
Из второго квадратного уравнения находим 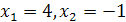 . Это действительные корни заданного уравнения.
. Это действительные корни заданного уравнения.
Биквадратные уравнения
Биквадратным называется уравнение вида 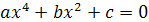 , где
, где 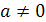 . Биквадратное уравнение решается методом введения новой переменной: положив
. Биквадратное уравнение решается методом введения новой переменной: положив 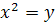 , придем к квадратному уравнению
, придем к квадратному уравнению 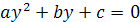 .
.
Пример 4. Решите уравнение 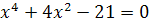 .
.
Решение. Положив 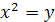 , получим квадратное уравнение
, получим квадратное уравнение 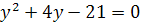 , откуда находим
, откуда находим 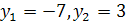 . Теперь задача сводится к решению уравнений
. Теперь задача сводится к решению уравнений 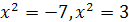 . Первое уравнение не имеет действительных корней, из второго находим
. Первое уравнение не имеет действительных корней, из второго находим 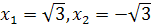 , которые являются корнями заданного биквадратного уравнения.
, которые являются корнями заданного биквадратного уравнения.
Решение задач с помощью составления уравнений
С помощью уравнений решаются многочисленные задачи, к которым приводят самые разнообразные вопросы физики, механики, экономики и многих других прикладных наук. Прежде всего напомним общий порядок решения задач с помощью уравнений.
1) Вводят переменные, т.е. буквами 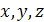 обозначают неизвестные величины, которые либо требуется найти в задаче, либо они необходимы для отыскания искомых величин.
обозначают неизвестные величины, которые либо требуется найти в задаче, либо они необходимы для отыскания искомых величин.
2) С помощью введенных переменных и данных в задаче чисел и их соотношений составляют уравнение.
3) Решают составленное уравнение и из полученных решений отбирают те, которые подходят по смыслу задачи.
4) Если буквами 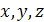 обозначили не искомые величины, то с помощью полученных решений находят ответ на вопрос задачи.
обозначили не искомые величины, то с помощью полученных решений находят ответ на вопрос задачи.
II. В уравнениях 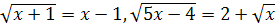 неизвестное
неизвестное 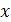 находится под знаком корня или под знаком возведения в дробную степень. Такие уравнения называют иррациональными.
находится под знаком корня или под знаком возведения в дробную степень. Такие уравнения называют иррациональными.
Решение иррациональных уравнений основано на следующем свойстве:
При возведении обеих частей уравнения в натуральную степень получается уравнение-следствие данного.
При возведении уравнения в натуральную степень могут появиться посторонние корни, поэтому необходимо делать проверку.
Если обе части уравнения 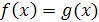 неотрицательны на множестве
неотрицательны на множестве 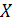 , то уравнение
, то уравнение 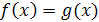 равносильно уравнению
равносильно уравнению 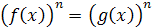 при
при 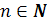 .
.
Пример 5 . Решите уравнение 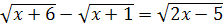 .
.
Решение. Возводя обе части уравнения в квадрат, получаем
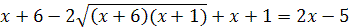
откуда 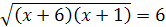 .
.
Возведем последнее уравнение в квадрат: 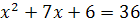 , или
, или 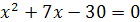 .
.
Корни этого уравнения 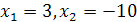 .
.
Проверка показывает, что 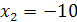 – посторонний корень.
– посторонний корень.
Ответ: 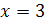 .
.
Пример 6 . Решите уравнение 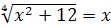 .
.
Решение. Возведем уравнение в четвертую степень: 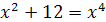 , откуда
, откуда 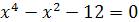 . Решим это биквадратное уравнение,
. Решим это биквадратное уравнение, 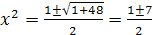 , т.е.
, т.е. 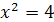 или
или 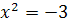 .
.
Уравнение 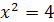 имеет два корня
имеет два корня 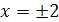 . Уравнение
. Уравнение 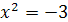 не имеет действительных корней. Так как при возведении обеих частей уравнения в четвертую степень могли появится посторонние корни, то нужно сделать проверку. При
не имеет действительных корней. Так как при возведении обеих частей уравнения в четвертую степень могли появится посторонние корни, то нужно сделать проверку. При 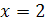 обе части уравнения равны 2, т.е.
обе части уравнения равны 2, т.е. 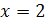 – корень уравнения. При
– корень уравнения. При 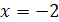 левая часть уравнения равна 2, а правая равна -2, т.е. -2 не является корнем уравнения.
левая часть уравнения равна 2, а правая равна -2, т.е. -2 не является корнем уравнения.
Ответ: 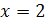 .
.
Пример 7. Решите уравнение 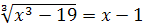 .
.
Решение. Возводя обе части уравнения в куб, получаем 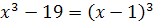 , откуда
, откуда
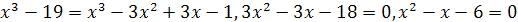 .
.
Корни этого уравнения 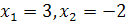 . Проверка показывает, что оба значения неизвестного являются корнями данного уравнения.
. Проверка показывает, что оба значения неизвестного являются корнями данного уравнения.
Пример 8. Выясните с помощью графиков, сколько корней имеет уравнение 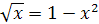 . Найти приближенные значения этих корней.
. Найти приближенные значения этих корней.
Решение. Построим на одном рисунке графики функций 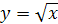 и
и 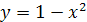 . Графики пересекаются в одной точке при
. Графики пересекаются в одной точке при 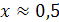 .
.
Задания к практической работе
Задание 1. Решите уравнения методом введения новой переменной:
1) 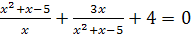 ;
;
2) 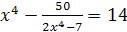 ;
;
3) 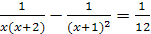 ;
;
4) 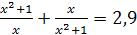 ;
;
5) 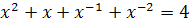 ;
;
6) 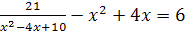 .
.
Задание 2. Решите уравнение, разложив левую часть на множители:
1) 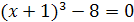 ;
;
2) 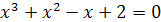 ;
;
3) 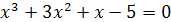 ;
;
4) 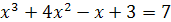 .
.
Задание 3. Решите задачу, составив к нему уравнение.
Для перевозки 60 т груза из одного места в другое затребовали некоторое количество машин. Ввиду неисправности дороги на каждую машину пришлось грузить на 0,5 т меньше, чем предполагалось, поэтому дополнительно потребовались 4 машины. Какое количество машин было затребовано?
Задание 4. Решите задачу, составив к нему уравнение.
Моторная лодка, обладающая скоростью движения 20 км/ч, прошла расстояние между двумя пунктами по реке туда и обратно без остановок за 6ч 15 мин. Расстояние между пунктами равно 60 км. Найти скорость течения реки.
Задание 5. Решите задачу, составив к нему уравнение.
Найти двухзначное число, зная, что цифра его единиц на 2 больше цифры десятков и что произведение искомого числа на сумму его цифр равно 144.
Задание 6. Решите задачу, составив к нему уравнение.
По обе стороны улицы, длиной в 1200 м, во вновь разбиваемом поселке лежат прямоугольные полосы земли, отведенные на участки, одна – шириной в 50 м, а другая – в 60 м. на сколько участков разбит весь поселок, если более узкая полоса содержит на 5 участков больше, чем широкая, при условии, что на узкой полосе каждый участок на 1200 м2 меньше, чем каждый участок на широкой полосе?
Задание 7. Решите задачу, составив к нему уравнение.
Через час после начала равномерного спуска воды в бассейне ее осталось 400 м3, а еще через три часа – 250 м3. Сколько воды было в бассейне?
Задание 8. Решите уравнение:
1. 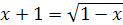 ; ;
| 2. | |
3. 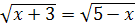 ; ;
| 4. | |
5. 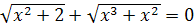 ; ;
| 6. | |
7.  ; ;
| 8. | |
9. 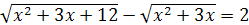 ; ;
| 10. | |
11. 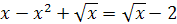 ; ;
| 12. | |
| 13.
| ||
| 14.
| 15. 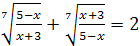 ; ;
| |
Задание 2. Выясните с помощью графиков, сколько корней имеет уравнение:
1. 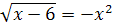 ; ;
| 2. 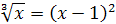 ; ;
|
3. 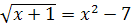 ; ;
| 4. 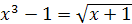 . .
|
Контрольные вопросы
1. Какие уравнения называют рациональными? Приведите примеры.
2. Назовите основные приемы решения рациональных уравнений.
3. Дайте определение биквадратным уравнениям.
4. Назовите алгоритм решения задач с помощью уравнений.
5. Дайте определение иррационального уравнения.
6. Какими методами можно решить иррациональные уравнения?
7. Каким методом можно решить уравнение 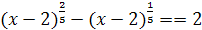 .
.
Рекомендуемая литература: 1.1, 1.4, 2.1
Практическая работа №31
Теоретический материал
Если ставится задача найти все общие решения двух уравнений с двумя переменными, то говорят, что надо решить систему уравнений. Каждая пара значений переменных, обращающая в верное равенство каждое уравнение системы, называется решением системы уравнений. Решить систему – значит найти все ее решения или доказать, что их нет.
Решать системы уравнений можно используя следующие методы:
Метод подстановки
Суть метода заключается в следующем:
1) Одно из уравнений системы преобразуют к виду, в котором 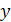 выражено через
выражено через 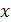 (или
(или 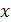 через
через 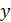 ).
).
2) Полученное выражение подставляют вместо 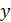 (или вместо
(или вместо 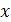 ) во второе уравнение. В результате получается уравнение с одной переменной.
) во второе уравнение. В результате получается уравнение с одной переменной.
3) Находят корни этого уравнения.
4) Воспользовавшись выражением 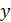 через
через 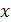 (или
(или 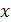 через
через 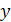 ), находят соответствующие значения
), находят соответствующие значения 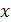 (или
(или 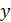 ).
).
Метод сложения
Поясним суть метода на примере.
Пример 1. Решите систему уравнений
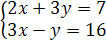 (31.1)
(31.1)
Решение. Умножив обе части второго уравнения системы на 31.3, получим систему равносильную данной.
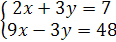 (31.2)
(31.2)
Сложим теперь оба уравнения полученной системы:
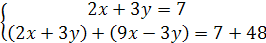 (31.3)
(31.3)
Преобразуем ее к виду:
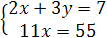
Из уравнения 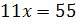 находим
находим 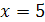 . Подставив это значение в уравнение
. Подставив это значение в уравнение 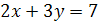 , находим
, находим  .
.
Итак, (5;-1) – решение системы (31.3), а значит, и решение равносильной ей системы (31.1).
Ответ: (5; -1),
Метод введения новых переменных
Применяется при решении систем двух уравнений с двумя переменными одним из следующих способов:
1) Вводится одна новая переменная только для одного уравнения системы;
2) Вводятся две новые переменные сразу для обоих уравнений.
Пример 2. Решите систему 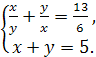
Решение. Положим 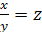 , тогда
, тогда 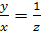 и первое уравнение системы примет вид
и первое уравнение системы примет вид 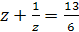 . Решим полученное уравнение относительно новой переменной
. Решим полученное уравнение относительно новой переменной 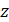 :
:
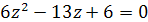 , откуда
, откуда 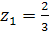 ,
, 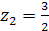 .
.
Таким образом, либо 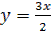 , либо
, либо 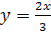 .
.
Итак, первое уравнение заданной системы распалось на два уравнения: 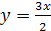 и
и 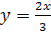 . В соответствии с этим нам предстоит решить теперь совокупность двух систем:
. В соответствии с этим нам предстоит решить теперь совокупность двух систем:
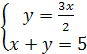 и
и 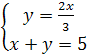
Из первой системы находим 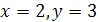 , из второй
, из второй 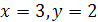 .
.
Ответ: (2; 3), (3,2).
Задания к практической работе
Задание 1. Решите систему уравнений:
1. 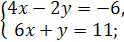
2. 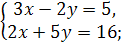
3. 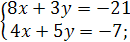
4. 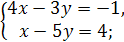
5. 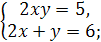
6. 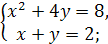
7. 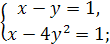
8. 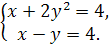
Задание 2. Решите систему уравнений:
1. 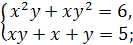
2. 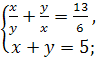
3. 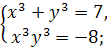
4. 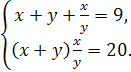
Задание 3. Решите систему уравнений методом замены переменных:
1) 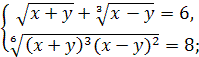
2) 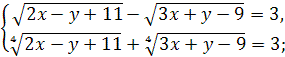
3) 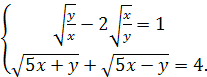
Контрольные вопросы
1. Что называется системой уравнений?
2. Что называется решением системы уравнений?
3. Перечислите методы решения систем уравнений.
4. Расскажите суть графического метода решения систем уравнений.
Рекомендуемая литература: 1.1, 1.3, 1.4.
Практическая работа №32
Теоретические сведения
Уравнения, в которых неизвестное содержится в показатели степени, называются показательными.
Решение показательных уравнений часто сводится к решению уравнения 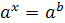 , где
, где 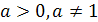 ,
, 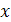 - неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием
- неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием 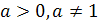 равны тогда и только тогда, когда равны их показатели.
равны тогда и только тогда, когда равны их показатели.
Решение показательных неравенств часто сводится к решению неравенств 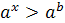 или
или 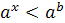 . Эти неравенства решаются с помощью свойства возрастания или убывания показательной функции: для возрастающей функции большему значению функции соответствует большее значение аргумента, а для убывающей функции большему значению функции соответствует меньшее значение аргумента.
. Эти неравенства решаются с помощью свойства возрастания или убывания показательной функции: для возрастающей функции большему значению функции соответствует большее значение аргумента, а для убывающей функции большему значению функции соответствует меньшее значение аргумента.
Пример 1. Решите уравнение 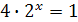 .
.
Решение. Запишем уравнение в виде 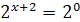 , откуда
, откуда 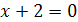 . Тогда
. Тогда 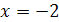 .
.
Ответ: 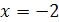 .
.
Пример 2. Решите уравнение 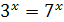 .
.
Решение. Так как 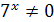 , то уравнение можно записать в виде
, то уравнение можно записать в виде 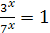 , откуда
, откуда 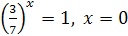 .
.
Ответ: x=0 .
Пример 3. Решите уравнение 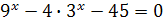 .
.
Решение. Заменой 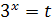 данное уравнение сводится к квадратному уравнению
данное уравнение сводится к квадратному уравнению 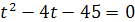 . Решая это уравнение, находим его корни:
. Решая это уравнение, находим его корни: 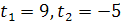 , откуда
, откуда 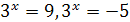 . Уравнение
. Уравнение 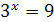 имеет корень
имеет корень 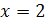 , а уравнение
, а уравнение 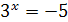 не имеет корней, так как показательная функция не может принимать отрицательные значения.
не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ: 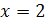 .
.
Пример 4. Решите графически уравнение 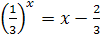 .
.
Решение. В одной системе координат построим графики функций 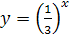 и
и 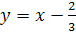 . Из рисунка видно, что графики этих функций пересекаются в точке с абсциссой
. Из рисунка видно, что графики этих функций пересекаются в точке с абсциссой 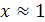 . Проверка показывает, что
. Проверка показывает, что 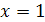 - корень данного уравнения:
- корень данного уравнения:
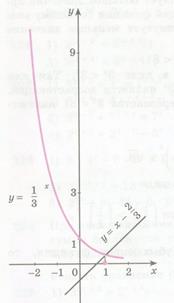 Рисунок 32.1 – графики
функций
Рисунок 32.1 – графики
функций
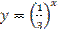 и и 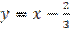
| 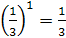 и и 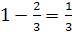 .
Ответ: .
Ответ: 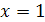 .
Покажем, что других корней нет. Функция .
Покажем, что других корней нет. Функция 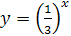 убывающая, а функция убывающая, а функция 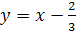 – возрастающая. Следовательно, при – возрастающая. Следовательно, при 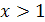 значение первой функции меньше значение первой функции меньше  , а второй больше , а второй больше  , при , при 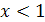 , наоборот, значения первой функции больше , наоборот, значения первой функции больше  , а второй меньше , а второй меньше  . Геометрически это означает, что графики этих функций при . Геометрически это означает, что графики этих функций при 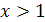 и и 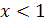 «расходятся» и потому не могут иметь точек пересечения при «расходятся» и потому не могут иметь точек пересечения при 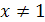 .
Уравнение, содержащее переменную под знаком логарифма или в основании логарифма, называется логарифмическим. .
Уравнение, содержащее переменную под знаком логарифма или в основании логарифма, называется логарифмическим.
|
При решении таких уравнений следует учитывать область определения и использовать определение логарифма.
Пример 5. Решите уравнение 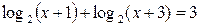 (32.1)
(32.1)
Решение. Предположим, что x – такое число, при котором равенство (1) является верным, т.е. x – корень уравнения (32.1). Тогда по свойству логарифма верно равенство: 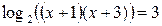 (32.2).
(32.2).
Из этого равенства по определению логарифма получаем 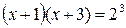
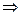
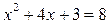 (3), т.е.
(3), т.е. 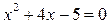 . Решая квадратное уравнение, получаем корни:
. Решая квадратное уравнение, получаем корни: 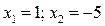 . Так как уравнение (32.3) является следствием исходного уравнения, то необходима проверка. Подставляем в левую часть исходного уравнения полученные корни:
. Так как уравнение (32.3) является следствием исходного уравнения, то необходима проверка. Подставляем в левую часть исходного уравнения полученные корни:
1. если x =1, то 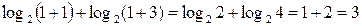 , равенство верно, значит x =1 – корень уравнения.
, равенство верно, значит x =1 – корень уравнения.
2. если x =-5, то 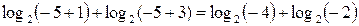 , по области определения логарифм от отрицательного числа не существует, значит x =-5 – не является корнем уравнения.
, по области определения логарифм от отрицательного числа не существует, значит x =-5 – не является корнем уравнения.
Ответ: 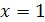 .
.
Решение уравнения (1) можно заменить решением равносильной ему системы: 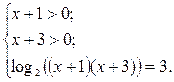
Пример 6. Решите уравнение 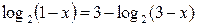 .
.
Решение. Перенесем логарифм из правой части в левую:
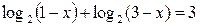
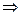
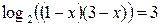
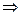
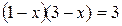 . Открываем скобки, решаем квадратное уравнение, получаем корни:
. Открываем скобки, решаем квадратное уравнение, получаем корни: 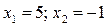 .
.
Проверка показывает, что только 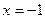 является корнем уравнения.
является корнем уравнения.
Ответ: 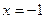 .
.
Пример 7. Решите уравнение 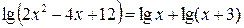 .
.
Решение. По свойству логарифмов: 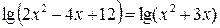
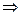
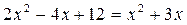
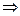
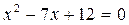
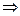
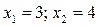 .
.
Проверка показывает, что оба корня являются корнями исходного уравнения.
Ответ: 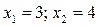 .
.
Пример 8. Решите уравнение 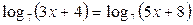
Решение: 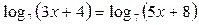
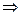
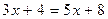
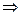
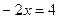
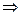
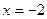
Выполняя проверку, видим, что выражения, стоящие под знаком логарифма при 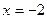 не имеют смысла.
не имеют смысла.
Ответ: корней нет.
Пример 9. Решите уравнение 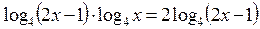
Решение: преобразовываем данное уравнение:
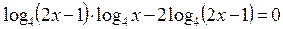 , вынесем за скобки общий множитель
, вынесем за скобки общий множитель
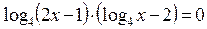 . Приравниваем каждый множитель левой части к нулю, решаем уравнения:
. Приравниваем каждый множитель левой части к нулю, решаем уравнения: 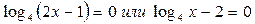 . Получаем:
. Получаем:
* 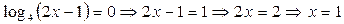 .
.
* 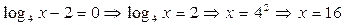
Проверка показывает, что оба значения являются корнями исходного уравнения.
Ответ: 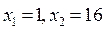 .
.
Пример 10. Решите уравнение 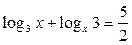
Решение: преобразовываем уравнение, используя формулу перехода к другому основанию 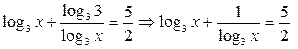 . Пусть
. Пусть 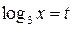 , тогда наше уравнение примет вид:
, тогда наше уравнение примет вид: 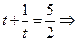
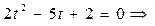
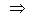
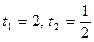 . Вернемся к замене:
. Вернемся к замене:
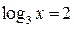 ; ;
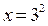 ; ;
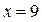 ОДЗ:
ОДЗ: 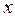 > 0; > 0; 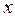 ≠1. ≠1.
| 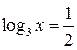 ; ;
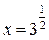 ; ;
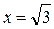
|
Найденные значения удовлетворяют ОДЗ.
Ответ: 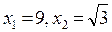 .
.
Задания к практической работе
Задание 1. Решите уравнение
| 1. | 2. | ||
| 3. | 4.
| ||
| 5. | 6.
| ||
| 7. | 8.
| ||
| 9. | 10.
| ||
| 11. | 12.
| ||
| 13. | 14.
| ||
| 15. | 16.
| ||
| 17. | 18. | ||
| 19. | 20.
| ||
| 21. | 22.
| ||
| 23. | 24.
| ||
25. 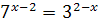 ; ;
| 26. | 27. 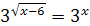 ; ;
| |
28. 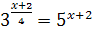 ; ;
| 29. | 30. 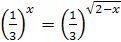 . .
| |
Задание 2. Решить графически уравнение:
1. 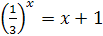 ; ;
| 2. 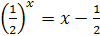 ; ;
|
3. 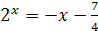 ; ;
| 4. 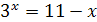 ; ;
|
5. 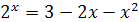 ; ;
| 6. 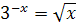 ; ;
|
7. 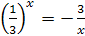 ; ;
| 8. 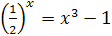 . .
|
Задание 3. Решите уравнения:
1. 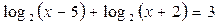 ; ;
| 2. 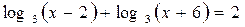 ; ;
|
3. 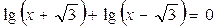 ; ;
| 4. 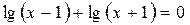 ; ;
|
5. 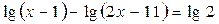 ; ;
| 6. 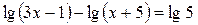 ; ;
|
7. 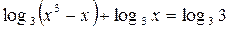 ; ;
| 8. 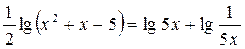 ; ;
|
9. 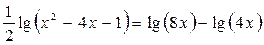 ; ;
| 10. 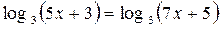 ; ;
|
11. 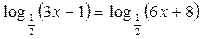 ; ;
| 12. 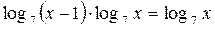 ; ;
|
13. 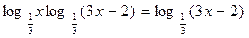 ; ;
| 14. 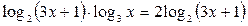 ; ;
|
15. 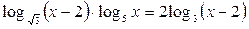 ; ;
| 16. 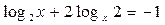 ; ;
|
17. 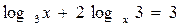 ; ;
| 18. 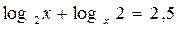
|
Контрольные вопросы
1. Дайте определение показательных уравнений. Приведите примеры.
2. Перечислите основные свойства показательной функции.
3. Какие простейшие приемы решения показательных уравнений вы знаете?
4. Дайте определение логарифма.
5. Назовите свойства логарифмов.
Рекомендуемая литература: 1.1, 2.1.
СПИСОК ЛИТЕРАТУРЫ
1. Основная:
1.1 Кремер, Н. Ш. Математика для колледжей : учебное пособие для
СПО / Н. Ш. Кремер, О. Г. Константинова, М. Н. Фридман ; под ред. Н. Ш. Кремера. — 10-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 346 с.
1.2 Богомолов, Н. В. Практические занятия по математике в 2 ч. Часть 1 : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 285 с.
1.3 Богомолов, Н. В. Практические занятия по математике в 2 ч. Часть 2 : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 217 с.
1.4 Богомолов, Н. В. Алгебра и начала анализа : учебное пособие для СПО / Н. В. Богомолов. — М. : Издательство Юрайт, 2018. — 200 с.
1.5 Далингер, В. А. Методика обучения стереометрии посредством решения задач : учебное пособие для СПО / В. А. Далингер. — 2-е изд., испр. и доп. — М. : Издательство Юрайт, 2018. — 370 с.
2. Дополнительная:
2.1 Шипачев, В. С. Математика : учебник и практикум для СПО / В. С. Шипачев ; под ред. А. Н. Тихонова. — 8-е изд., перераб. и доп. — М. : Издательство Юрайт, 2017. — 447 с.
2.2 Кремер, Н. Ш. Теория вероятностей и математическая статистика : учебник и практикум для академического бакалавриата / Н. Ш. Кремер. — 4-е изд., перераб. и доп. — М. : Издательство Юрайт, 2017. — 514 с.
Учебное издание
ОУДп.01 МАТЕМАТИКА: АЛГЕБРА, НАЧАЛА
Дата: 2018-12-28, просмотров: 408.
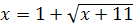 ;
;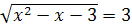 ;
;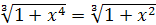 ;
;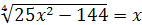 ;
;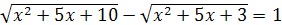 ;
;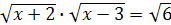 ;
;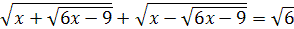 ;
;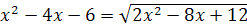 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;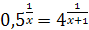 ;
;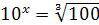 ;
; ;
;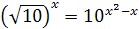 ;
;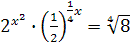 ;
;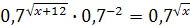 ;
;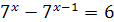 ;
;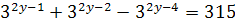 ;
;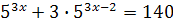 ;
;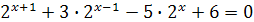 ;
;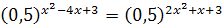 ;
;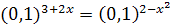 ;
;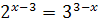 ;
;