Цель: формирование навыков преобразования и решения уравнений.
Вид работы: индивидуальный.
Время выполнения: 2 часа.
Теоретические сведения
Уравнения, имеющие одно и то же множество корней, называются равносильными.
Уравнения, не имеющие корней, также являются равносильными.
Например, уравнения 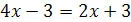 и
и 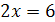 равносильны, так как каждое из них имеет только один корень
равносильны, так как каждое из них имеет только один корень 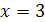 . Уравнения
. Уравнения 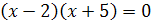 и
и 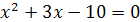 также равносильны, так как они имеют одни и те же корни
также равносильны, так как они имеют одни и те же корни 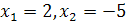 . Уравнения
. Уравнения 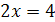 и
и 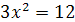 не равносильны, так как первое имеет корень
не равносильны, так как первое имеет корень 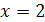 , а второе – корни
, а второе – корни 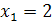 и
и 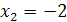 .
.
Два уравнения равносильны, если каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого уравнения.
Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.
Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.
При этих преобразованиях исходное уравнение заменяется на равносильное ему уравнение.
Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называют следствием первого уравнения. Иначе, если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения.
Из этого определения и определения равносильности уравнений следует, что:
1) если два уравнения равносильны, то каждое из них является следствием другого;
2) если каждое из двух уравнений является следствием другого, то эти уравнения равносильны.
При решении уравнений главное – не потерять корни, а наличие посторонних корней можно установить проверкой.
Посторонние корни могут получиться при умножении обеих частей уравнения на выражение, содержащее неизвестное.
Потеря корней может произойти при делении обеих частей уравнения на выражение, содержащее неизвестное.
При решении уравнения можно делать только такие его преобразования, при которых не происходит потерь корней. Если при этом получаются уравнения – следствия данного, то необходима проверка найденных корней.
Пример 1. Решить уравнение 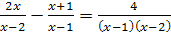 .
.
Решение. Умножив обе части уравнения на общий знаменатель всех трех дробей, т.е. на 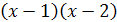 , получим
, получим 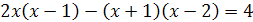 , откуда
, откуда 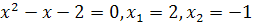 .
.
Проверка. 1) При 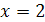 знаменатели двух дробей уравнения равны нулю. Поэтому
знаменатели двух дробей уравнения равны нулю. Поэтому 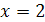 не является корнем данного уравнения.
не является корнем данного уравнения.
2) При 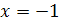 левая часть уравнения равна
левая часть уравнения равна 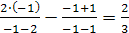 , правая часть равна
, правая часть равна 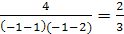 .
.
Таким образом, корнем уравнения является 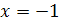 , а корень
, а корень 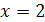 - корнем данного уравнения не является, его называют посторонним корнем.
- корнем данного уравнения не является, его называют посторонним корнем.
Пример 2. Решите уравнение 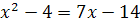 .
.
Решение. Преобразуем данное уравнение так:
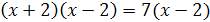 ,
,
Откуда 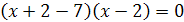 , т.е.
, т.е. 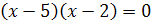 , следовательно,
, следовательно, 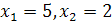 .
.
Задания к практической работе
Задание 1. Равносильны ли следующие уравнения:
1. 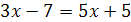 и
и 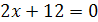 ;
;
2. 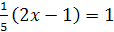 и
и 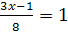 ;
;
3. 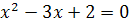 и
и 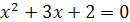 ;
;
4. 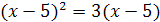 и
и 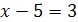 ;
;
5. 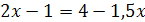 и
и  ;
;
6. 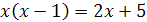 и
и 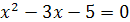 ;
;
7. 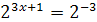 и
и 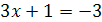 ;
;
8. 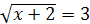 и
и 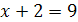 .
.
Задание 2. Решите уравнения:
1. 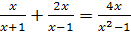 ; ;
| 2. 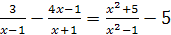 ; ;
|
3. 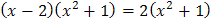 ; ;
| 4. 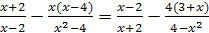 . .
|
Контрольные вопросы
1. Какие уравнения называются равносильными? Приведите примеры.
2. Какое уравнение называется следствием другого? Приведите примеры.
3. Какие методы преобразования уравнений вы знаете?
Рекомендуемая литература: 1.1, 1.3, 1.4, 2.1.
Практическая работа №30
Дата: 2018-12-28, просмотров: 668.