Цель: формирование навыков применения формул для нахождения характеристик гармонических механических колебаний, понять качественные задачи, основываясь на закономерностях волновых и колебательных движений.
Вид работы: индивидуальный.
Время выполнения: 2 часа.
Теоретический материал
Если точка M движется по окружности радиуса R (рис.26.1) с посто-
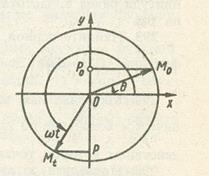 Рисунок 26.1 – Движение точки
Рисунок 26.1 – Движение точки
| янной угловой скоростью 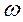 , то проекция P точки M на ось Oy совершает по этой оси колебательное движение по закону: , то проекция P точки M на ось Oy совершает по этой оси колебательное движение по закону: 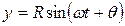 (26.1)
Движение точки P называется простым гармоническим колебанием. Величина R (амплитуда колебания) выражает максимальное отклонение колеблющейся точки P от начала координат; (26.1)
Движение точки P называется простым гармоническим колебанием. Величина R (амплитуда колебания) выражает максимальное отклонение колеблющейся точки P от начала координат; 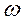 – угловая скорость точки M в радианах в секунду; t – время в секундах, за которое точка M перемещается – угловая скорость точки M в радианах в секунду; t – время в секундах, за которое точка M перемещается
|
При 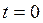 радиус-вектор
радиус-вектор 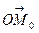 образует с осью Ox угол
образует с осью Ox угол 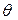 . Через t секунд радиус-вектор повернется на угол
. Через t секунд радиус-вектор повернется на угол 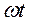 и образует с осью Ox угол
и образует с осью Ox угол 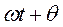 . Следовательно, проекция точки, равномерно движущейся по окружности радиуса R с угловой скоростью
. Следовательно, проекция точки, равномерно движущейся по окружности радиуса R с угловой скоростью 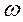 , совершает гармонические колебания с амплитудой R и начальной фазой
, совершает гармонические колебания с амплитудой R и начальной фазой 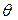 .
.
Время T, в течение которого точка P пройдет через все фазы, а точка M совершит один полный оборот по окружности, называется периодом гармонического колебания, т.е. T есть период функции 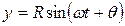 . Так как точка P за время T совершает один полный оборот, т.е. описывает дугу
. Так как точка P за время T совершает один полный оборот, т.е. описывает дугу 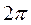 радиан, то за единицу времени она опишет угол
радиан, то за единицу времени она опишет угол 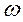 , равный
, равный 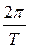 радиан, поэтому угловая скорость:
радиан, поэтому угловая скорость:
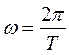 (26.1).
(26.1).
Отсюда следует, что
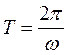 (26.2).
(26.2).
Величина, обратная периоду колебания T , т.е. 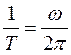 , называется частотой колебания. Частота колебания показывает число колебаний n, совершаемых точкой в секунду:
, называется частотой колебания. Частота колебания показывает число колебаний n, совершаемых точкой в секунду:
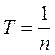 (26.3).
(26.3).
Пример 1. Составить уравнение гармонического колебания, если амплитуда равна 10, период равен 0,5, а начальная фаза равна 1,5.
Решение: по формуле (26.1) находим 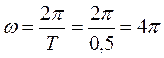 . Подставляя R =10;
. Подставляя R =10;  =1,5;
=1,5; 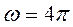 в равенство (26.1), получим
в равенство (26.1), получим 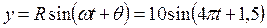 .
.
Ответ: 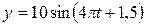 .
.
Пример 2. Найти период, амплитуду и начальную фазу следующих функций:
1) 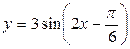 ; ;
| 2) 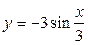 ; ;
| 3) 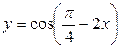
|
Решение: 1) Здесь R=3, 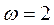 ,
, 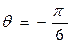 . Период T находим из соотношения (26.3), т.е.
. Период T находим из соотношения (26.3), т.е. 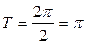 .
.
2) Здесь 
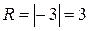 ,
, 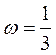 ,
, 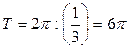 . Для вычисления начальной фазы запишем данную функцию в виде
. Для вычисления начальной фазы запишем данную функцию в виде 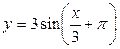 , откуда
, откуда 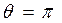 .
.
3) Преобразуем данную функцию следующим образом: 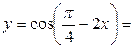
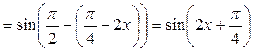 , откуда
, откуда  ,
, 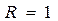 ,
, 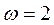 ,
, 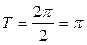 .
.
Задания к практической работе
Задание 1. Составить уравнение гармонического колебания, если амплитуда равна 5, частота колебания равна 3, а начальная фаза равна 0,8.
Задание 2. Найти период, амплитуду и начальную фазу следующих функций 1) 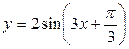 ; 2)
; 2) 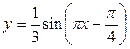 ; 3)
; 3) 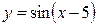 .
.
Задание 3. Материальная точка массы 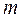 совершает простое гармоническое колебание по закону
совершает простое гармоническое колебание по закону 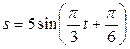 . Найти силу
. Найти силу 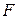 , под действием которой точка совершает это движение в момент
, под действием которой точка совершает это движение в момент 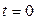 .
.
Задание 4. Привести к виду 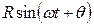 выражения: 1)
выражения: 1) 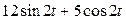 ;
;
2) 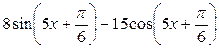 .
.
Задание 5. Найти амплитуду и начальную фазу сумм следующих колебаний: 1) 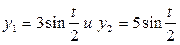 ; 2)
; 2)  ;
;
3) 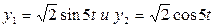 .
.
Контрольные вопросы
1. Назвать закон, по которому проекция точки совершает колебательное движение.
2. Дать определение периода гармонического колебания.
3. Как называется величина обратная периоду колебания?
Рекомендуемая литература: 1.1, 1.3, 1,4, 2.1.
СПИСОК ЛИТЕРАТУРЫ
1. Основная:
1.1 Кремер, Н. Ш. Математика для колледжей : учебное пособие для
СПО / Н. Ш. Кремер, О. Г. Константинова, М. Н. Фридман ; под ред. Н. Ш. Кремера. — 10-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 346 с.
1.2 Богомолов, Н. В. Практические занятия по математике в 2 ч. Часть 1 : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 285 с.
1.3 Богомолов, Н. В. Практические занятия по математике в 2 ч. Часть 2 : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 217 с.
1.4 Богомолов, Н. В. Алгебра и начала анализа : учебное пособие для СПО / Н. В. Богомолов. — М. : Издательство Юрайт, 2018. — 200 с.
1.5 Далингер, В. А. Методика обучения стереометрии посредством решения задач : учебное пособие для СПО / В. А. Далингер. — 2-е изд., испр. и доп. — М. : Издательство Юрайт, 2018. — 370 с.
2. Дополнительная:
2.1 Шипачев, В. С. Математика : учебник и практикум для СПО / В. С. Шипачев ; под ред. А. Н. Тихонова. — 8-е изд., перераб. и доп. — М. : Издательство Юрайт, 2017. — 447 с.
2.2 Кремер, Н. Ш. Теория вероятностей и математическая статистика : учебник и практикум для академического бакалавриата / Н. Ш. Кремер. — 4-е изд., перераб. и доп. — М. : Издательство Юрайт, 2017. — 514 с.
Учебное издание
Дата: 2018-12-28, просмотров: 605.