Основными критериями оценки выполненной обучающимся и представленной для проверки работы являются:
1. Степень соответствия выполненного задания поставленным требованиям.
2. Структурирование и комментирование практической работы.
3. Уникальность выполнение работы (отличие от работ коллег).
4. Успешные ответы на контрольные вопросы.
«отлично» - оформление соответствует требованиям, критерии выдержаны, защита всего перечня контрольных вопросов.
«хорошо» - оформление соответствует требованиям, критерии выдержаны, защита только 80 % контрольных вопросов.
«удовлетворительно» - оформление соответствует требованиям, критерии выдержаны, защита только 61 % контрольных вопросов.
Практическая работа №18
Тема: Преобразование суммы тригонометрических функций в произведение
Цель: формирование навыков использования основных тригонометрических формул при преобразовании тригонометрических выражений.
Вид работы: индивидуальный.
Время выполнения: 4 часа.
Теоретические сведения
Для преобразования алгебраических сумм тригонометрических функций в произведение используются формулы:
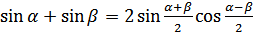 (18.1)
(18.1)
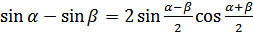 (18.2)
(18.2)
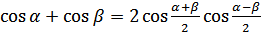 (18.3)
(18.3)
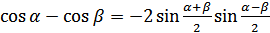 (18.4)
(18.4)
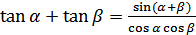
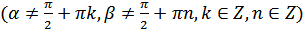 (18.5)
(18.5)
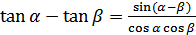
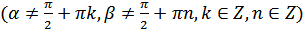 (18.6)
(18.6)
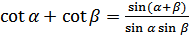
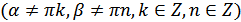 (18.7)
(18.7)
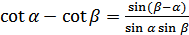
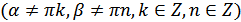 (18.8)
(18.8)
Полезно также знать формулу для преобразования в произведение выражения 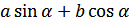 (a и b – любые действительные числа, не равные нулю). Эта формула имеет вид:
(a и b – любые действительные числа, не равные нулю). Эта формула имеет вид:
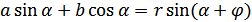 (18.9)
(18.9)
где 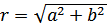 , аргумент
, аргумент 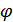 определяется из условий
определяется из условий 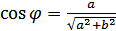 ,
, 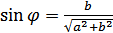 .
.
 ;
; 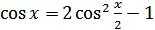 (18.10)
(18.10)
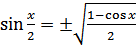 (18.11)
(18.11)
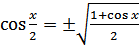 (18.12)
(18.12)
С помощью формул (18.11) и (18.12) можно вычислять значения синуса и косинуса половинного аргумента — по заданному значению косинуса аргумента х.
Разделив почленно равенство (18.11) на равенство (18.12), получим формулу
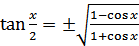 (18.13)
(18.13)
В формулах (18.11), (18.12) и (18.13) знак перед радикалом зависит от того, в какой координатной четверти находится угол  .
.
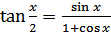 ,
, 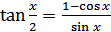 (18.14)
(18.14)
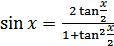 (18.15)
(18.15)
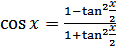 (18.16)
(18.16)
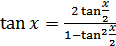 , при
, при 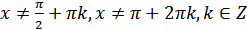 (18.17)
(18.17)
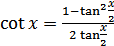 , при
, при 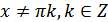 (18.18)
(18.18)
Пример 1. Вычислить: 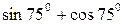
Решение. 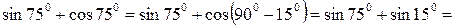
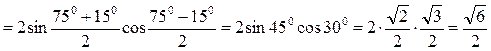 .
.
Пример 2. Преобразовать в произведение 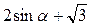
Решение. 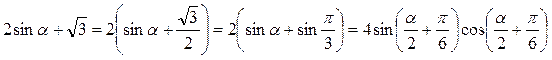 .
.
Задания к практической работе
Задание 1. Упростить выражение:
1. 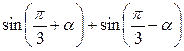 ; ;
| 2. 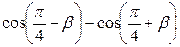 ; ;
|
3. 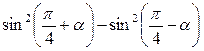 ; ;
|
|
Задание 2. Вычислить:
1. 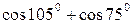 ; ;
| 2. 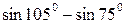 ; ;
|
3. 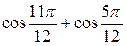 ; ;
| 4. 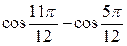 ; ;
|
5. 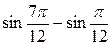 ; ;
| 6. 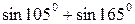 ; ;
|
7. 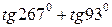 ; ;
| 8. 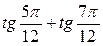 . .
|
Задание 3. Преобразовать в произведение:
1.  ; ;
| 2. 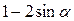 ; ;
|
3. 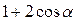 ; ;
| 4. 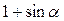 ; ;
|
5. 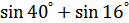 ; ;
| 6. 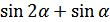 ; ;
|
7. 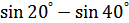 ; ;
| 8. 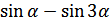 ; ;
|
9. 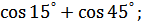
| 10. 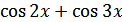 ; ;
|
11. 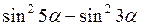 ; ;
| 12. 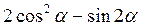 ; ;
|
13. 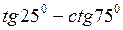 ; ;
| 14. 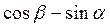 . .
|
Задание 4. Доказать тождество:
1. 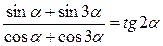 ; ;
| 2. 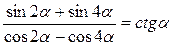 . .
|
Задание 5. Упростить выражение:
1. 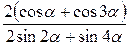 ; ;
| 2. 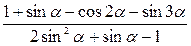 . .
|
Задание 6. Найти значения выражения:
1. 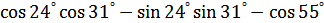 ;
;
2.  ;
;
3. 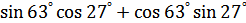 ;
;
4. 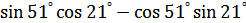 .
.
Задание 7. Вычислить без помощи таблиц:
1. 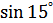 ; ;
| 2. 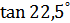 ; ;
| 3. 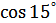 . .
|
Контрольные вопросы
1. Назвать формулу суммы синусов двух функций.
2. Назвать формулу разности синусов двух функций.
3. Назвать формулу суммы косинусов двух функций.
4. Назвать формулу разности косинусов двух функций.
5. Назвать формулу суммы тангенсов двух функций.
6. Назвать формулу разности тангенсов двух функций.
Рекомендуемая литература: 1.1, 1.3, 1.4,1.5, 2.1.
Практическая работа №19
Тема: Преобразование произведения тригонометрических функций в сумму
Цель: формирование навыков использования основных тригонометрических формул при преобразовании тригонометрических выражений.
Вид работы: индивидуальный.
Время выполнения: 4 часа.
Теоретические сведения
Для преобразования произведения тригонометрических функций в сумму применяются формулы:
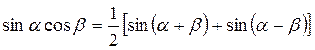 (19.1)
(19.1)
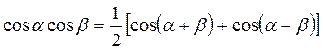 (19.2)
(19.2)
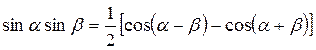 (19.3)
(19.3)
Пример 1. Преобразовать в алгебраическую сумму а) 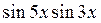 ;
;
б) 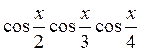 .
.
Решение. а) По формуле (3) получим:
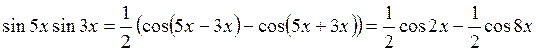 .
.
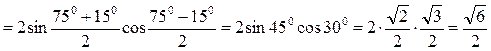 .
.
б) Используя формулу (2) дважды, получим:
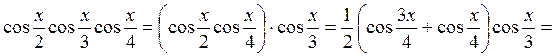
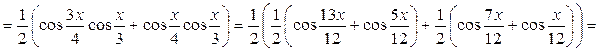
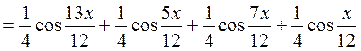 .
.
Пример 2. Представить в виде сумм первых степеней следующие тригонометрические функции: а) 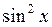 ; б)
; б) 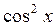 ; в)
; в) 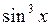 .
.
Решение. а) 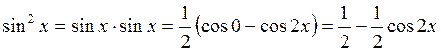 .
.
б) 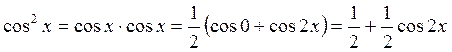 .
.
в) 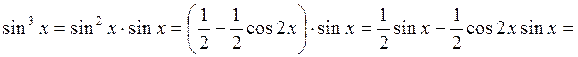
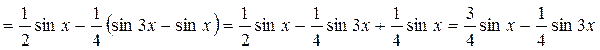
Отсюда получаем формулу утроенного аргумента: 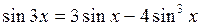 .
.
Задания к практической работе
Задание 1. Преобразовать в алгебраическую сумму:
1. 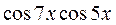 ; ;
| 2. 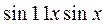 ; ;
|
3. 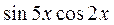 ; ;
|
|
5. 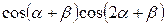
| 6. 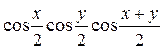
|
Задание 2. Вычислить:
1. 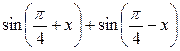 ; ;
| 2. 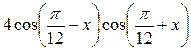 ; ;
|
3. 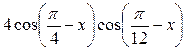
| 4. 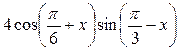
|
Задание 3. Представить в виде сумм первых степеней:
1. 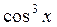 ; ;
| 2. 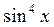 ; ;
|
3. 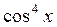 ; ;
| 4. 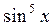 ; ;
|
5. 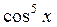 . .
|
Контрольные вопросы
1. Назвать формулы преобразования произведения тригонометрических функций в сумму.
2. Назвать формулу утроенного аргумента.
Рекомендуемая литература: 1.1, 1.3, 1.4,1.5, 2.1.
Практическая работа №20
Дата: 2018-12-28, просмотров: 365.
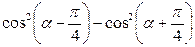 .
.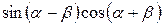 .
.