ОУДп.01 МАТЕМАТИКА: АЛГЕБРА, НАЧАЛА
МАТЕМАТИЧЕСКОГО АНАЛИЗА, ГЕОМЕТРИЯ
Методические указания по выполнению практических работ
по дисциплине ОУДп.01 Математика: алгебра и начала
математического анализа, геометрия
для обучающихся по всем специальностям
очной формы обучения
(часть 3)
Составитель С.И. Москалевская,
Преподаватель высшей квалификационной категории
Тюмень
ТИУ
2018
ОУДп.01 Математика: алгебра, начала математического анализа, геометрия методические указания по выполнению практических работ по дисциплине ОУДп.01 Математика: алгебра, начала математического анализа, геометрия для обучающихся по всем специальностям очной формы обучения (часть 3) / сост. Москалевская С.И.; Тюменский индустриальный университет. – Тюмень: Издательский центр БИК, ТИУ, 2018. –31 с.
Ответственный редактор: Т.М. Белкина, председатель цикловой комиссии общеобразовательных дисциплин.
Методические указания рассмотрены и рекомендованы к изданию на заседании цикловой комиссии общеобразовательных дисциплин
«18» января 2018 года, протокол №1
Аннотация
Методические указания по дисциплине ОУДп.01Математика: алгебра, начала математического анализа, геометрия предназначены для обучающихся по всем специальностям очной формы обучения.
Методические указания по дисциплине ОУДп.01 Математика: алгебра, начала математического анализа, геометрия составлены в соответствии с рабочей программой и состоят из содержания практических работ, пояснительной записки, общих требований по выполнению практических работ, критериев оценки выполнения и контрольных вопросов.
Методические указания могут оказать помощь преподавателям в организации самостоятельных работ, а также могут использоваться обучающимися при подготовке к занятиям и экзамену.
 |
Содержание
| Пояснительная записка | 4 |
| Общие требования к выполнению и оформлению практических работ | 4 |
| Критерии оценки практических работ | 5 |
| Практическая работа №18 Преобразование суммы тригонометрических функций в произведение | 5 |
| Практическая работа №19 Преобразование произведения тригонометрических функций в сумму | 8 |
| Практическая работа №20 Простейшие тригонометрические уравнения | 9 |
| Практическая работа № 21 Простейшие тригонометрические неравенства | 13 |
| Практическая работа №22 Обратные тригонометрические функции: арксинус, арккосинус, арктангенс | 15 |
| Практическая работа №23 Примеры зависимостей между переменными в реальных процессах из смежных дисциплин. Построение и чтение графиков функций | 17 |
| Практическая работа №24 Обратные функции и их графики | 21 |
| Практическая работа №25 Преобразования графика функции | 24 |
| Практическая работа №26 Гармонические колебания. Прикладные задачи | 27 |
| Список литературы | 30 |
Пояснительная записка
Методические указания по выполнению практических работ составлены в соответствии с рабочей программой по дисциплине ОУДп.01 Математика: алгебра, начала математического анализа, геометрия на базе основного общего образования.
Практические работы занимают важное место при изучении дисциплины ОУДп.01 Математика: алгебра и начала математического анализа, геометрия. Цель изучения дисциплины состоит в формировании знаний, практических умений и навыков решения элементарных математических задач.
В результате выполнения практических работ обучающийся должен:
иметь представление:
- о месте и роли математики в современном мире, общности ее понятий и представлений;
- о логическом строении дисциплины;
- о междисциплинарной связи математики со специальными дисциплинами;
знать и уметь:
- теоретические разделы каждой темы;
уметь:
- решать примеры и задачи по каждой теме.
Методические указания по выполнению практических работ состоят из пояснительной записки, критериев оценки работы, общих требований к выполнению и оформлению практических занятий, содержания практических занятий, которые снабжены основными теоретическими положениями, заданиями, контрольными вопросами и списком литературы.
На выполнение каждой работы отводится определенное количество часов в соответствии с тематическим планом.
Форма отчетности указана для каждого практического занятия.
Методические указания по выполнению практических работ окажут помощь преподавателям в организации и управлении работой обучающихся в процессе занятий, а обучающиеся могут использовать их как пособие для повторения изученного материала, подготовке к экзамену.
ОБЩИЕ ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ
ПРАКТИЧЕСКИХ РАБОТ
Практические задания должны оформляться в отдельной тетради и содержать:
- тему, цель, вид работы, время выполнения практического задания;
- условия заданий;
- необходимые расчетные формулы, понятия;
- подробные решения заданий;
- для успешной защиты отчета по практическим заданиям обучающийся должен правильно ответить на рекомендуемые контрольные вопросы, проявить навыки решения задач и умение иллюстрировать теоретический материал расчетами для выполненных заданий.
- отчет должен заключаться выводом о практической работе.
Практическая работа №18
Тема: Преобразование суммы тригонометрических функций в произведение
Цель: формирование навыков использования основных тригонометрических формул при преобразовании тригонометрических выражений.
Вид работы: индивидуальный.
Время выполнения: 4 часа.
Теоретические сведения
Для преобразования алгебраических сумм тригонометрических функций в произведение используются формулы:
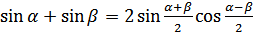 (18.1)
(18.1)
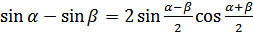 (18.2)
(18.2)
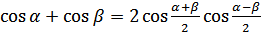 (18.3)
(18.3)
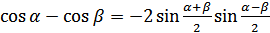 (18.4)
(18.4)
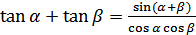
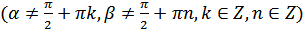 (18.5)
(18.5)
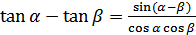
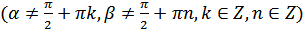 (18.6)
(18.6)
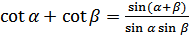
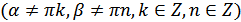 (18.7)
(18.7)
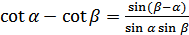
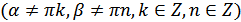 (18.8)
(18.8)
Полезно также знать формулу для преобразования в произведение выражения 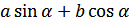 (a и b – любые действительные числа, не равные нулю). Эта формула имеет вид:
(a и b – любые действительные числа, не равные нулю). Эта формула имеет вид:
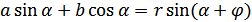 (18.9)
(18.9)
где 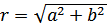 , аргумент
, аргумент 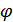 определяется из условий
определяется из условий 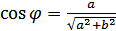 ,
, 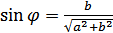 .
.
 ;
; 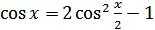 (18.10)
(18.10)
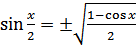 (18.11)
(18.11)
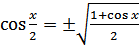 (18.12)
(18.12)
С помощью формул (18.11) и (18.12) можно вычислять значения синуса и косинуса половинного аргумента — по заданному значению косинуса аргумента х.
Разделив почленно равенство (18.11) на равенство (18.12), получим формулу
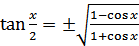 (18.13)
(18.13)
В формулах (18.11), (18.12) и (18.13) знак перед радикалом зависит от того, в какой координатной четверти находится угол  .
.
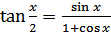 ,
, 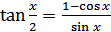 (18.14)
(18.14)
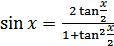 (18.15)
(18.15)
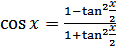 (18.16)
(18.16)
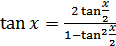 , при
, при 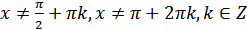 (18.17)
(18.17)
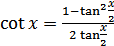 , при
, при 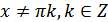 (18.18)
(18.18)
Пример 1. Вычислить: 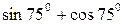
Решение. 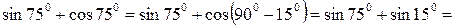
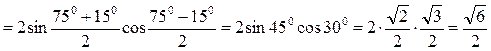 .
.
Пример 2. Преобразовать в произведение 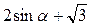
Решение. 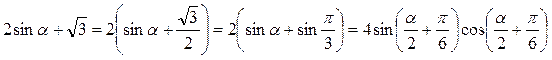 .
.
Задания к практической работе
Задание 1. Упростить выражение:
1. 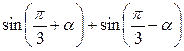 ; ;
| 2. 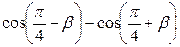 ; ;
|
3. 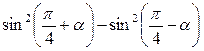 ; ;
|
|
Задание 2. Вычислить:
1. 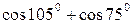 ; ;
| 2. 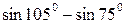 ; ;
|
3. 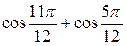 ; ;
| 4. 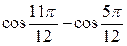 ; ;
|
5. 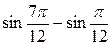 ; ;
| 6. 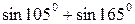 ; ;
|
7. 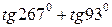 ; ;
| 8. 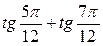 . .
|
Задание 3. Преобразовать в произведение:
1.  ; ;
| 2. 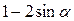 ; ;
|
3. 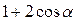 ; ;
| 4. 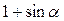 ; ;
|
5. 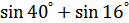 ; ;
| 6. 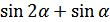 ; ;
|
7. 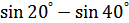 ; ;
| 8. 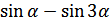 ; ;
|
9. 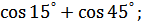
| 10. 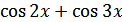 ; ;
|
11. 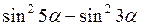 ; ;
| 12. 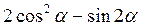 ; ;
|
13. 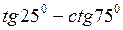 ; ;
| 14. 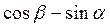 . .
|
Задание 4. Доказать тождество:
1. 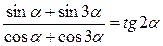 ; ;
| 2. 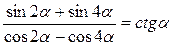 . .
|
Задание 5. Упростить выражение:
1. 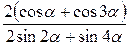 ; ;
| 2. 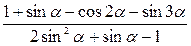 . .
|
Задание 6. Найти значения выражения:
1. 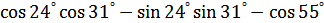 ;
;
2.  ;
;
3. 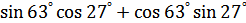 ;
;
4. 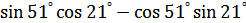 .
.
Задание 7. Вычислить без помощи таблиц:
1. 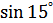 ; ;
| 2. 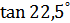 ; ;
| 3. 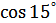 . .
|
Контрольные вопросы
1. Назвать формулу суммы синусов двух функций.
2. Назвать формулу разности синусов двух функций.
3. Назвать формулу суммы косинусов двух функций.
4. Назвать формулу разности косинусов двух функций.
5. Назвать формулу суммы тангенсов двух функций.
6. Назвать формулу разности тангенсов двух функций.
Рекомендуемая литература: 1.1, 1.3, 1.4,1.5, 2.1.
Практическая работа №19
Тема: Преобразование произведения тригонометрических функций в сумму
Цель: формирование навыков использования основных тригонометрических формул при преобразовании тригонометрических выражений.
Вид работы: индивидуальный.
Время выполнения: 4 часа.
Теоретические сведения
Для преобразования произведения тригонометрических функций в сумму применяются формулы:
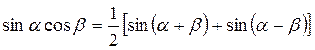 (19.1)
(19.1)
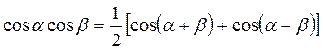 (19.2)
(19.2)
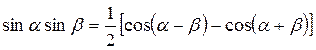 (19.3)
(19.3)
Пример 1. Преобразовать в алгебраическую сумму а) 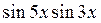 ;
;
б) 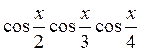 .
.
Решение. а) По формуле (3) получим:
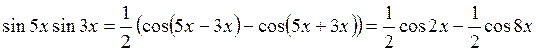 .
.
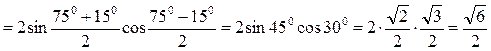 .
.
б) Используя формулу (2) дважды, получим:
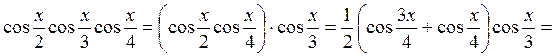
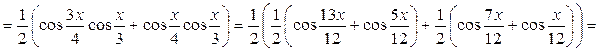
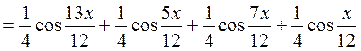 .
.
Пример 2. Представить в виде сумм первых степеней следующие тригонометрические функции: а) 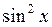 ; б)
; б) 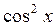 ; в)
; в) 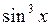 .
.
Решение. а) 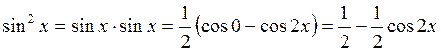 .
.
б) 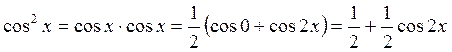 .
.
в) 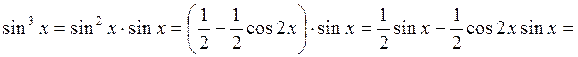
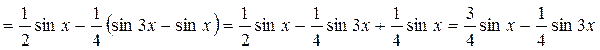
Отсюда получаем формулу утроенного аргумента: 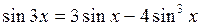 .
.
Задания к практической работе
Задание 1. Преобразовать в алгебраическую сумму:
1. 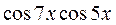 ; ;
| 2. 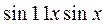 ; ;
|
3. 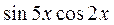 ; ;
|
|
5. 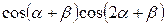
| 6. 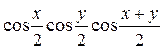
|
Задание 2. Вычислить:
1. 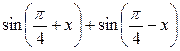 ; ;
| 2. 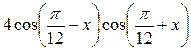 ; ;
|
3. 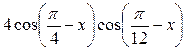
| 4. 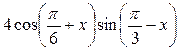
|
Задание 3. Представить в виде сумм первых степеней:
1. 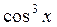 ; ;
| 2. 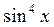 ; ;
|
3. 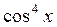 ; ;
| 4. 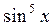 ; ;
|
5. 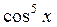 . .
|
Контрольные вопросы
1. Назвать формулы преобразования произведения тригонометрических функций в сумму.
2. Назвать формулу утроенного аргумента.
Рекомендуемая литература: 1.1, 1.3, 1.4,1.5, 2.1.
Практическая работа №20
Теоретические сведения
Простейшими тригонометрическими уравнениям называют уравнения 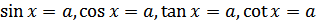 , где
, где 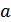 - данное число.
- данное число.
Решить простейшее тригонометрическое уравнение – значит найти множество всех значений аргумента (дуг или углов), при которых данная тригонометрическая функция принимает заданное значение 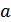 .
.
Формула для корней уравнения 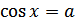 , где
, где 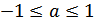 , имеет вид:
, имеет вид:
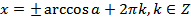 . (20.1)
. (20.1)
Частные случаи:
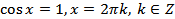 ; (20.2)
; (20.2)
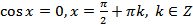 ; (20.3)
; (20.3)
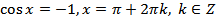 . (20.4)
. (20.4)
Формула для корней уравнения 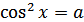 , где
, где 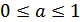 , имеет вид:
, имеет вид:
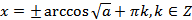 . (20.5)
. (20.5)
Формула для корней уравнения 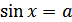 , где
, где 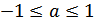 , имеет вид:
, имеет вид:
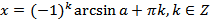 . (20.6)
. (20.6)
Частные случаи:
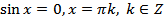 ; (20.7)
; (20.7)
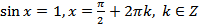 ; (20.8)
; (20.8)
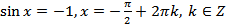 . (20.9)
. (20.9)
Формула для корней уравнения 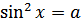 , где
, где 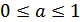 , имеет вид:
, имеет вид:
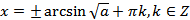 . (20.10)
. (20.10)
Формула для корней уравнения 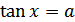 , имеет вид:
, имеет вид:
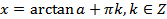 . (20.11)
. (20.11)
Частные случаи:
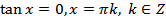 ; (20.12)
; (20.12)
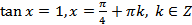 ; (20.13)
; (20.13)
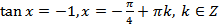 . (20.14)
. (20.14)
Формула для корней уравнения 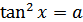 , где
, где 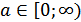 , имеет вид:
, имеет вид:
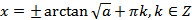 . (20.15)
. (20.15)
Пример 1. Решить уравнения: 1) 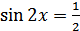 ; 2)
; 2) 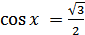 ;
;
3) 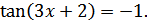
Решение. 1) 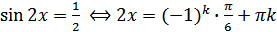 , отсюда следует, что множество корней данного уравнения имеет вид
, отсюда следует, что множество корней данного уравнения имеет вид 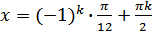 .
.
2) Так как 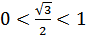 и
и 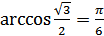 , то
, то 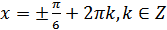
3) 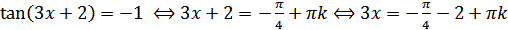 . Тогда множество корней уравнения имеет вид
. Тогда множество корней уравнения имеет вид 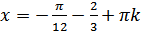 .
.
Пример 2. Решить уравнение 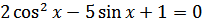 .
.
Решение. Заменяя 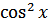 на
на 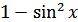 , получаем
, получаем 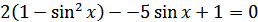 или
или 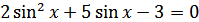 .
.
Обозначая 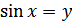 , получаем
, получаем 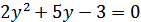 , откуда
, откуда 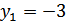 ,
, 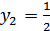 .
.
1) 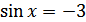 - уравнение не имеет корней, так как
- уравнение не имеет корней, так как 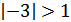 ;
;
2) 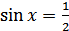 ,
, 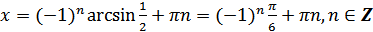 .
.
Таким образом, 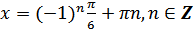 .
.
Пример 3. Решить уравнение 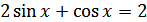 .
.
Решение. Используя формулы 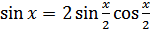 ,
, 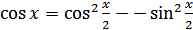 и записывая правую часть уравнения в виде
и записывая правую часть уравнения в виде 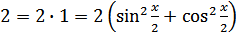 , получаем
, получаем
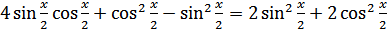 ,
, 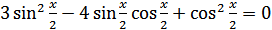 .
.
Поделив это уравнение на 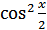 , получим равносильное уравнение
, получим равносильное уравнение 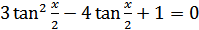 . Обозначая
. Обозначая 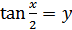 , получим уравнение
, получим уравнение 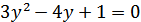 , откуда
, откуда 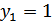 ,
, 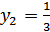 .
.
1) 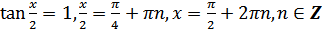 ;
;
2) 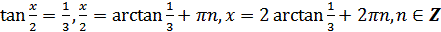 .
.
Задания к практической работе
Задание 1. Решить уравнения:
1. 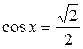 ; ;
| 2. | 3. 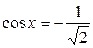 ; ;
| |
4. 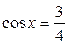 ; ;
| 5. | 6. 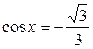 ; ;
| |
7. 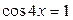 ; ;
| 8. | 9. 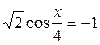 ; ;
| |
10. 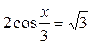 ; ;
| 11. | 12. 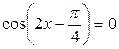 ; ;
| |
| 13. | 14. | ||
| 15. | 16. | ||
| 17. | 18. | ||
| 19. | 20. | ||
| 21. | 22. | ||
Задание 2. Найти все корни уравнения 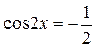 на отрезке
на отрезке 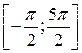 .
.
Задание 3. Решить уравнение:
1. 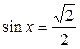 ; ;
| 2. | 3. 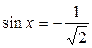 ; ;
| |
4. 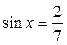 ; ;
| 5. | 6. 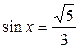 ; ;
| |
7. 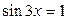 ; ;
| 8. | 9. 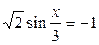 ; ;
| |
10. 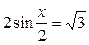 ; ;
| 11. | 12. 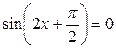 ; ;
| |
| 13. | 14. | ||
| 15. | 16. | ||
| 17. | 18. | ||
| 19. | 20. | ||
| 21. | 22. | ||
Задание 4. Найти все корни уравнения 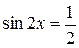 на отрезке
на отрезке 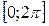 .
.
Задание 5. Решить уравнение:
1. 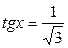 ; ;
| 2. | 3. 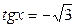 ; ;
| |
4. 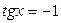 ; ;
| 5. | 6. 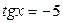 ; ;
| |
7.  ; ;
| 8. | 9. 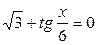 ; ;
| |
| 10. | 11. | ||
| 12. | 13. | ||
| 14. | 15. | ||
Задание 6. Найти наименьший положительный и наибольший отрицательный корни уравнения 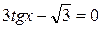 .
.
Контрольные вопросы
1. Какие уравнения называются тригонометрическими?
2. Что называется корнем тригонометрического уравнения?
3. По каким формулам находят решения простейших тригонометрических уравнений?
Рекомендуемая литература: 1.1, 1.3, 1.4.
Практическая работа №21
Теоретические сведения
Пример 1. Решить неравенство: 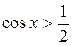 .
.
Решение. По определению 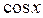 – это абсцисса точки единичной окружности. Чтобы решить неравенство
– это абсцисса точки единичной окружности. Чтобы решить неравенство 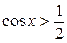 , нужно выяснить, какие точки единичной окружности имеют абсциссу, большую
, нужно выяснить, какие точки единичной окружности имеют абсциссу, большую 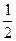 .
.
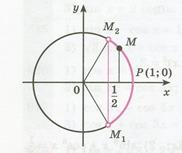 Рисунок 21.1 - Решение неравенства
Рисунок 21.1 - Решение неравенства 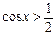
| Абсциссу, равную 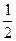 , имеют две точки единичной окружности , имеют две точки единичной окружности 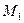 и и 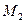 (рис. 21.1) . Точка
(рис. 21.1) . Точка 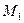 получается поворотом точки получается поворотом точки 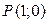 на угол на угол 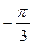 , а также на углы , а также на углы 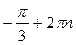 , где , где 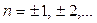 . Точка . Точка 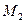 получается поворотом точки получается поворотом точки 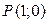 на угол на угол 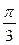 , а также на углы , а также на углы 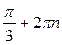 , где , где 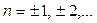 . .
|
Абсциссу, большую 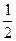 , имеют все точки
, имеют все точки 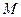 дуги единичной окружности, лежащие правее прямой
дуги единичной окружности, лежащие правее прямой 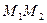 . Таким образом, решениями неравенства
. Таким образом, решениями неравенства 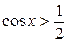 являются все числа
являются все числа 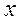 из промежутка
из промежутка 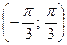 . Все решения данного неравенства – множество интервалов:
. Все решения данного неравенства – множество интервалов: 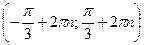 ,
, 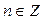 .
.
Пример 2. Решить неравенство: 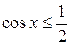 .
.
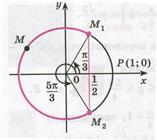 Рисунок 21.2 - Решение неравенства
Рисунок 21.2 - Решение неравенства 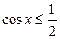
| Решение. Абсциссу, не большую 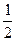 , имеют все точки дуги , имеют все точки дуги 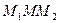 единичной окружности (рис. 2). Поэтому решениями неравенства единичной окружности (рис. 2). Поэтому решениями неравенства 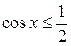 являются числа являются числа 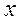 , которые принадлежат отрезку , которые принадлежат отрезку 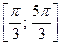 . Все решения данного неравенства – множе- . Все решения данного неравенства – множе-
|
ство отрезков: 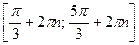 ,
, 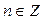 .
.
Пример 3. Решить неравенство: 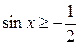 .
.
Решение. Ординату, не меньшую 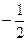 , имеют все точки дуги
, имеют все точки дуги 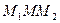 единичной окружности (рис. 21.3).
единичной окружности (рис. 21.3).
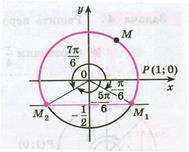 Рисунок 21.3 - Решение
неравенства
Рисунок 21.3 - Решение
неравенства 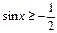
| Поэтому решениями неравенства 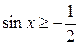 являются числа являются числа 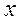 , которые принадлежат отрезку , которые принадлежат отрезку 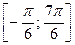 . Все решения данного неравенства – множество отрезков: . Все решения данного неравенства – множество отрезков: 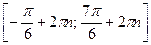 , , 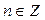 . .
|
Отметим, что все точки окружности, лежащие ниже прямой 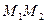 , имеют ординату, меньшую
, имеют ординату, меньшую 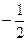 (рис. 21.3). Поэтому все числа
(рис. 21.3). Поэтому все числа 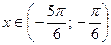 являются решениями неравенства
являются решениями неравенства 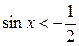 .
.
Все решения этого неравенства – интервалы: 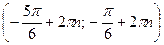 ,
, 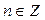 .
.
Пример 4. Решить неравенство: 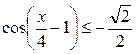 .
.
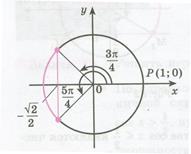 Рисунок 21.4 - Решение неравенства
Рисунок 21.4 - Решение неравенства 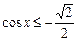
| Решение. Обозначим 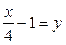 . Решая неравенство . Решая неравенство 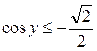 (рис. 21.4), находим (рис. 21.4), находим 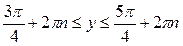 , , 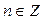 . Заменяя . Заменяя 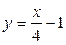 , получаем: , получаем: 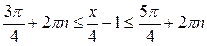 , ,
|
откуда 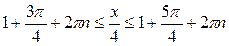
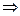
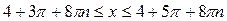 ,
, 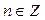 .
.
Ответ: 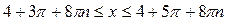 ,
, 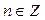 .
.
Задания к практической работе
Задание 1. Решить неравенство:
1. 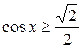 ; ;
| 2. 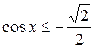 ; ;
| 3. 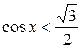 ; ;
|
4. 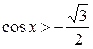 ; ;
| 5. 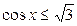 ; ;
| 6. 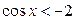 ; ;
|
7. 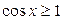 ; ;
| 8. 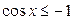 ; ;
| 9. 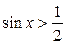 ; ;
|
10.  ; ;
| 11. 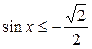
| 12. 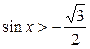
|
13. 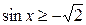 ; ;
| 14. 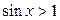 ; ;
| 15. 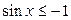 ; ;
|
16. 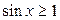 ; ;
| 17. 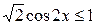 ; ;
| 18. 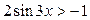 ; ;
|
19. 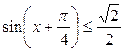 ; ;
| 20. 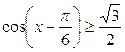 ; ;
| 21. 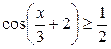 . .
|
Контрольные вопросы
1. Какие неравенства называются тригонометрическими?
2. Какими способами можно решить простейшее тригонометрическое неравенство?
Рекомендуемая литература: 1.1, 1.3, 1.4.
Практическая работа №22
Теоретические сведения
Функция 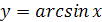
Перечислим основные свойства функции 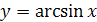 .
.
1) Область определения – отрезок 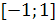 .
.
2) Множество значений – отрезок 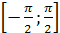 .
.
3) Функция 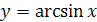 возрастает.
возрастает.
4) Функция 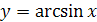 является нечетной, так как
является нечетной, так как 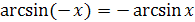 .
.
График функции 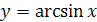 симметричен графику функции
симметричен графику функции 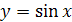 ,
, 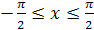 относительно прямой
относительно прямой 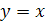 (рис. 22.1).
(рис. 22.1).
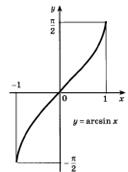
Рисунок 22.1 - График функции 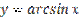
Функция 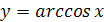
Перечислим основные свойства функции 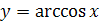 .
.
1) Область определения – отрезок 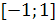 .
.
2) Множество значений – отрезок 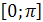 .
.
3) Функция 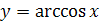 убывает.
убывает.
График функции 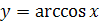 симметричен графику функции
симметричен графику функции 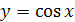 ,
, 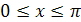 относительно прямой
относительно прямой 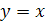 (рис. 22.2).
(рис. 22.2).
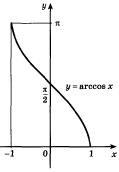
Рис. 22.2 - График функции 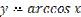
Функция 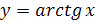
Перечислим основные свойства функции  .
.
1) Область определения – множество 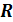 всех действительных чисел.
всех действительных чисел.
2) Множество значений – интервал 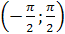 .
.
3) Функция  возрастает.
возрастает.
4) Функция  является нечетной:
является нечетной: 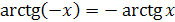 .
.
График функции  получается из графика функции
получается из графика функции 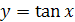 ,
, 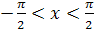 , симметрией относительно прямой
, симметрией относительно прямой 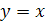 (рис. 22.3).
(рис. 22.3).
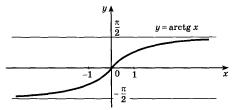
Рисунок 22.3 - График функции 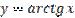
Пример 1. Найти область определения функции 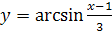 .
.
Решение. Так как функция 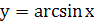 определена при
определена при 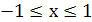 , то функция
, то функция 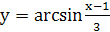 определена для тех значений
определена для тех значений 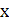 , для которых выполняются неравенства
, для которых выполняются неравенства 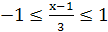 . Отсюда
. Отсюда 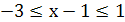 ,
, 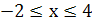 .
.
Пример 2. Решить уравнение 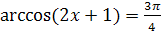 .
.
Решение. Так как 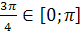 , то по определению арккосинуса числа данное уравнение равносильно уравнению
, то по определению арккосинуса числа данное уравнение равносильно уравнению 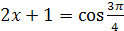 , откуда
, откуда 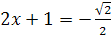 ,
, 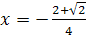 .
.
Задания к практической работе
Задание 1. Найти область определения функции:
1. 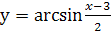 ;
;
2. 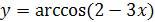 ;
;
3. 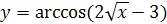 ;
;
4. 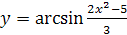 .
.
Задание 2. Доказать, что график функции 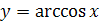 симметричен относительно точки
симметричен относительно точки 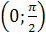 .
.
Задание 3. Решить уравнение:
1. 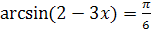 ;
;
2. 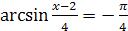 ;
;
3. 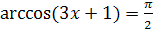 ;
;
4. 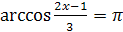 ;
;
5. 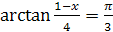 ;
;
6. 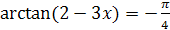 .
.
Контрольные вопросы
1. Дать определение функции 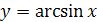 .
.
2. Дать определение функции 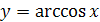 .
.
3. Дать определение функции  .
.
4. Дать определение функции 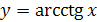 .
.
5. Перечислить свойства обратных тригонометрических функций.
Рекомендуемая литература: 1.1, 1.3, 1.4.
Практическая работа №23
Тема: Примеры зависимостей между переменными в реальных процессах из смежных дисциплин. Построение и чтение графиков функций
Цель: формирование представления о графике функции, способы практического применения графиков функций
Вид работы: индивидуальный.
Время выполнения: 2 часа.
Теоретические сведения
Определение.
1. Функция - это закон, по которому каждому значению элемента x из некоторого множества X ставится в соответствие единственный элемент y из множества Y.
2. Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом, а переменную у - зависимой переменной. Значение у, соответствующее заданному значению х, называют значением функции.
Записывают: у = f (х). Буквой f обозначается данная функция, т. е. функциональная зависимость между переменными х и у; f (х) есть значение функции, соответствующее значению аргумента х. Говорят также, что f (х) есть значение функции в точке х. Все значения, которые принимает независимая переменная, образуют область определения функции. Все значения, которые принимает функция f (х) (при х, принадлежащих области ее определения), образуют область значений функции.
Способы задания функции
Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у = f (х), где f (х) - некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента.
График функции.
Пусть функция задана аналитически формулой у = f (х). Если на координатной плоскости отметить все точки, обладающие следующим свойством: абсцисса точки принадлежит области определения функции, а ордината равна соответствующему значению функции, то множество точек (х; f (x)) есть график функции.
На практике для построения графика функции составляют таблицу значений функции при некоторых значениях аргумента, наносят на плоскость соответствующие точки и соединяют полученные точки линией. При этом предполагают, что график функции является плавной линией, а найденные точки достаточно точно показывают ход изменения функции. Преимуществом графического изображения по сравнению с табличным являются его наглядность и легкая обозримость; недостатком - малая степень точности. Большое практическое значение имеет удачный выбор масштабов. По графику можно найти (приблизительно) значение функции и для тех значений аргумента, которые не помещены в таблице.
Пример 1. График описывает движение парусной яхты, которая первую часть пути прошла под парусом. Спустив парус, она продолжила движение.
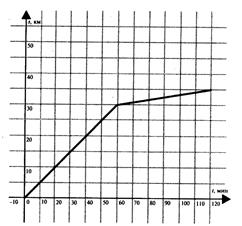 Рисунок 23.1 - Движение яхты
Рисунок 23.1 - Движение яхты
| 1) Найти скорость яхты «под парусом » и «без паруса» (выраженные в км/ч); 2) На каком расстоянии от начала движения находилась яхта через 50 минут, через 2 часа? 3) Сколько времени потребуется яхте на обратный путь, если она будет двигаться с той же скоростью, что и на первом участке «под парусом»? |
Решение: 1) Под парусом яхта прошла 30 км за 60 мин, т.е. за 1 ч., значит её скорость была 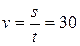 км/ч. Без паруса яхта прошла 5 км за 60 мин, значит её скорость была 5 км/ч.
км/ч. Без паруса яхта прошла 5 км за 60 мин, значит её скорость была 5 км/ч.
Ответ: скорость яхты «под парусом » 30 км/ч и скорость яхты «без паруса» 5 км/ч.
2) На графике найдем точку с абсциссой равной 50. Найдем ординату этой точки. Она равна 25. Получили, что за 50 минут яхта пройдет 25 км. Аналогично, за 120 мин - 35 км.
Ответ: за 50 минут яхта пройдет 25 км, за 120 мин яхта пройдет 35 км.
3) Обратный путь составляет 35 км. Скорость яхты 30 км/ч. Найдем время обратного пути: 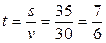 ч, что составляет 1 час 10 минут.
ч, что составляет 1 час 10 минут.
Ответ: 1 ч 10 мин.
Задания к практической работе
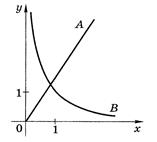 Рисунок 23.2 –
зависимости функций
Рисунок 23.2 –
зависимости функций
| Задание 1. На рисунке схематически изображены графики двух зависимостей: 1) зависимости расстояния, пройденного автомобилем от времени движения при постоянной скорости; 2) зависимости времени движения автомобиля между двумя городами от скорости движения. Какой из графиков является графиком первой зависимости? |
Задание 2. Турист отправился из лагеря к озеру, отдохнул у озера и вер-
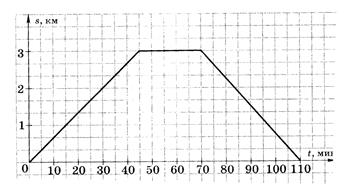
| нулся обратно. На рисунке изображен график движения туриста (по горизонтальной оси откладывается время, по вертикальной – расстояние , на котором находится турист от лагеря ). Найдите скорость туриста на обратном пути, выразив её в км/ч. |
Рисунок 23.3 – Движение туриста
Задание 3. На рисунке изображен график функции  . Из приведенных утверждений выберите верное.
. Из приведенных утверждений выберите верное.
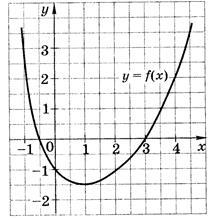
| А.  Б. Функция
Б. Функция 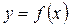 убывает на промежутке убывает на промежутке 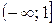 В.
В. 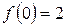 Г. Функция принимает наименьшее значение при
Г. Функция принимает наименьшее значение при 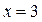
|
Рисунок 23.4 – График функции
Задание 4. Плот плывет по реке. На рисунке изображен график его движе-
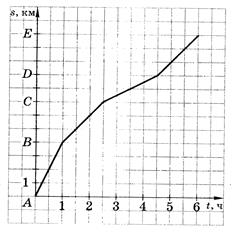
| ния: по горизонтальной оси откладывается время движения t, по вертикальной – расстояние s которое проплыл плот. На каком участке пути скорость течения наибольшая?
|
Рисунок 23.5 – Движение плота
Задание 5. Туристы отправились с турбазы на озеро, провели там 2 ч и вернулись обратно. Какой из графиков описывает зависимость пройденного туристами расстояния от времени, которое они провели в походе?
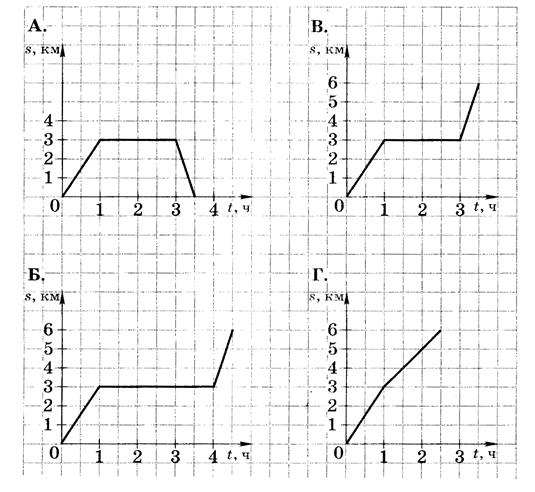
Рисунок 23.6 – Графики зависимостей
Контрольные вопросы
1. Дать определение функции.
2. Назвать способы задания функции.
3. Дать определение графика функции.
Рекомендуемая литература: 1.1, 1.3, 1.4
Практическая работа №24
Теоретические сведения
Если функция y=f(x) принимает каждое свое значение только при одном значении x, то эту функцию называют обратимой.
Пусть функция y=f(x) монотонна в своей области определения D ( f ). Тогда каждому значению 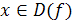 соответствует единственное значение
соответствует единственное значение 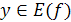 и обратно: каждое значение
и обратно: каждое значение 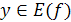 соответствует единственному
соответствует единственному 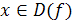 . Значит, в этом случае можно построить новую функцию, определенную на E(f) и такую, что каждому
. Значит, в этом случае можно построить новую функцию, определенную на E(f) и такую, что каждому 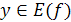 ставится в соответствие
ставится в соответствие 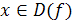 , удовлетворяющее уравнению y=f(x). Эта новая функция называется обратной по отношению к функции y = f ( x ).
, удовлетворяющее уравнению y=f(x). Эта новая функция называется обратной по отношению к функции y = f ( x ).
Для нахождения функции, обратной данной y=f(x), надо выразить х через у: x=g (у), а затем записать полученную функцию в общепринятой форме y = g(x).
Отметим, что если функции y=f(х) и y=g(x) являются взаимно обратными, то область определения функции f совпадает с множеством значений функции g и, наоборот, область определения функции g совпадает с множеством значений функции f, т. e. 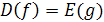 и
и 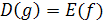 .
.
Графики взаимно обратных функций симметричны относительно прямой у=х (рис. 24.1).
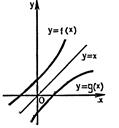
Рисунок 24.1 - Графики взаимно обратных функций
Рассмотрим, например, функцию 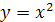 , заданную на промежутке
, заданную на промежутке 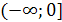 . На этом промежутке функция убывает и принимает все значения из множества [0; +∞). Следовательно, для данной функции существует обратная. Из уравнения
. На этом промежутке функция убывает и принимает все значения из множества [0; +∞). Следовательно, для данной функции существует обратная. Из уравнения 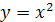 находим
находим 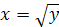 или
или 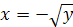 ; так как переменная х может принимать только неположительные значения, то искомая обратная функция имеет вид
; так как переменная х может принимать только неположительные значения, то искомая обратная функция имеет вид 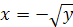 . Поменяв обозначения х на у и у на х, получим формулу
. Поменяв обозначения х на у и у на х, получим формулу 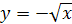 , где
, где 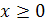 , с помощью которой и задается обратная функция.
, с помощью которой и задается обратная функция.
Если же рассматривать функцию 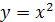 , заданную на промежутке [0; +∞), то обратной для нее служит функция
, заданную на промежутке [0; +∞), то обратной для нее служит функция 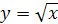 , где
, где 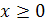 . На рисунке 24.2 изображены график функции
. На рисунке 24.2 изображены график функции 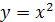 при
при 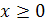 и график обратной ей функции.
и график обратной ей функции.
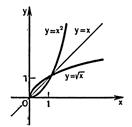
Рисунок 24.2 - График функции 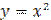 и обратной ей функции
и обратной ей функции
Пример. Задать формулой функцию, обратную f. Построить графики данной и обратной ей функции, если функция f задана формулой:
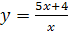 , где
, где 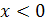 .
.
Решение. Выразив х через у, имеем 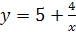 ,
, 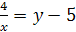 ,
, 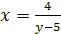 . Заменив х на у, а у на х, получим
. Заменив х на у, а у на х, получим 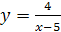 . Найдем область определения обратной функции, она совпадает с множеством значений заданной функции. Этим множеством служит промежуток
. Найдем область определения обратной функции, она совпадает с множеством значений заданной функции. Этим множеством служит промежуток 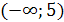 (рис.24.3). Итак,
(рис.24.3). Итак, 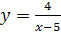 ,
, 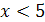 - функция, обратная данной.
- функция, обратная данной.
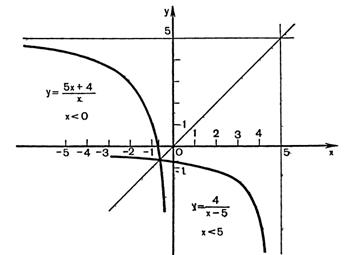
Рисунок 24.3 - Графики обратных функций
Задания к практической работе
Задание 1. Найти функцию, обратную к данной:
1. 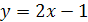 ;
;
2. 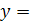 −5x+4;
−5x+4;
3. 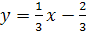 ;
;
4. 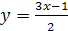 ;
;
5. 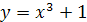 ;
;
6. 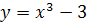 ;
;
7. 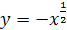 ;
;
8. 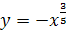 ;
;
9. 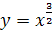 ;
;
10. 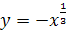 .
.
Задание 2. Найти область определения и множество значений функции, обратной к данной:
1. 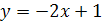 ;
;
2. 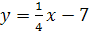 ;
;
3. 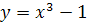 ;
;
4. 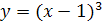 ;
;
5. 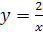 ;
;
6. 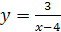 .
.
Задание 3. Функция 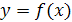 задана графиком (рис. 24.4, а, б, в, г). Построить график функции, обратной к данной.
задана графиком (рис. 24.4, а, б, в, г). Построить график функции, обратной к данной.
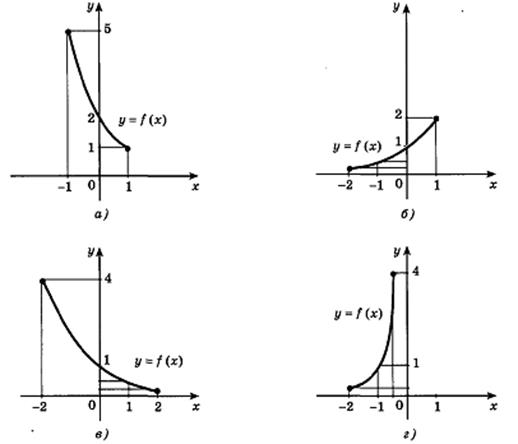
Рисунок 24.4 – Графики функций
Задание 4. На одном рисунке построить график данной функции и функции, обратной к данной; найти область определения и множество значений каждой из них:
1. 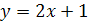 ;
;
2.  ;
;
3. 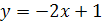 ;
;
4. 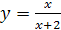 ;
;
5. 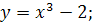
6. 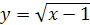 ;
;
7. 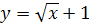 ;
;
8. 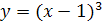 .
.
Контрольные вопросы
1. Дать определение обратной функции.
2. Как определить область определения обратной функции?
3. Как определить множество значений обратной функции?
4. Является ли монотонная функция обратимой?
5. Как можно построить график обратной функции?
Рекомендуемая литература: 1.1, 1.3.
Практическая работа №25
Тема: Преобразования графика функции
Цель: формирование навыков построения графиков функций и выполнения их основных преобразований.
Вид работы: индивидуальный
Время выполнения: 2 часа
Теоретический материал
Если известен график функции 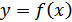 , то с помощью некоторых преобразований плоскости (параллельного переноса, осевой и центральной симметрии и т.п.) можно построить графики более сложных функций.
, то с помощью некоторых преобразований плоскости (параллельного переноса, осевой и центральной симметрии и т.п.) можно построить графики более сложных функций.
1) График функции 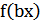 получается сжатием графика
получается сжатием графика 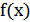 в
в 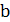 раз к оси
раз к оси 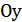 при
при 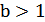 или растяжением в
или растяжением в  раз от этой оси
раз от этой оси 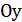 при
при 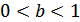 (рис.25.1).
(рис.25.1).
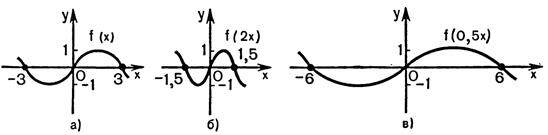
Рисунок 25.1 - Сжатие и растяжение
2) График функции 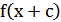 получается параллельным переносом графика
получается параллельным переносом графика 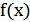 в отрицательном направлении оси
в отрицательном направлении оси 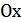 на
на 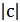 при
при 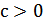 и в положительном направлении на
и в положительном направлении на 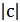 при
при 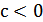 (рис.25.2).
(рис.25.2).
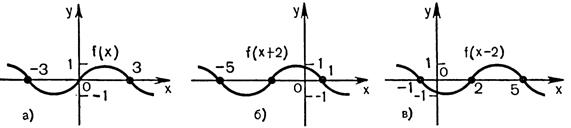
Рисунок 25.2 - Движение вдоль оси Ox
3) График функции 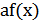 получается растяжением графика
получается растяжением графика 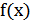 вдоль оси
вдоль оси 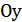 в
в 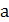 раз при
раз при 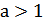 и сжатием вдоль этой оси в
и сжатием вдоль этой оси в  раз при
раз при 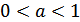 (рис.25.3).
(рис.25.3).
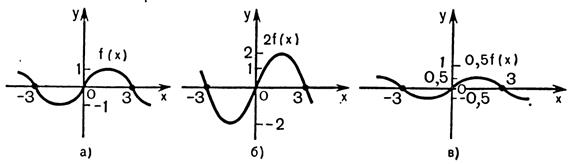
Рисунок 25.3 - Сжатие и растяжение
4) График функции 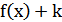 получается параллельным переносом графика
получается параллельным переносом графика 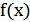 в положительном направлении оси
в положительном направлении оси 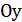 на
на 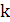 при
при 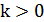 и в отрицательном направлении этой оси на
и в отрицательном направлении этой оси на 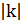 при
при 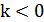 (рис.25.4).
(рис.25.4).
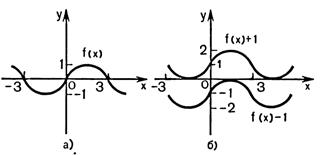
Рисунок 25.4 - Движение вдоль оси Oy
5) График функции 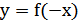 получается симметричным отображением графика
получается симметричным отображением графика 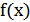 относительно оси
относительно оси 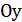 (рис.25.5).
(рис.25.5).
6) График функции 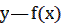 получается симметричным отображением графика
получается симметричным отображением графика 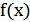 относительно оси
относительно оси 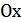 (рис.25.6).
(рис.25.6).
7) График функции 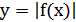 получается из графика функции
получается из графика функции 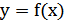 следующим образом: часть графика
следующим образом: часть графика 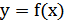 , лежащая над осью
, лежащая над осью 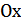 , сохраняется, часть его, лежащая под осью
, сохраняется, часть его, лежащая под осью 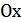 , отображается симметрично относительно оси
, отображается симметрично относительно оси 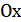 (рис.25.7).
(рис.25.7).
8) График функции 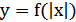 получается из графика функции
получается из графика функции 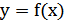 следующим образом: при
следующим образом: при 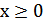 график
график 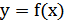 сохраняется, а при
сохраняется, а при 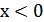 полученная часть графика отображается симметрично относительно оси
полученная часть графика отображается симметрично относительно оси 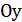 (рис.25.8).
(рис.25.8).
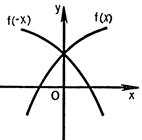
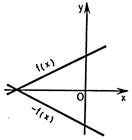
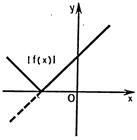
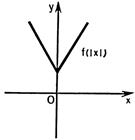
Рисунок 25.5 - Рисунок 25.6 - Рисунок 25.7 - Рисунок 25.8 -
симметричное симметричное симметричное симметричное
отображение отображение отображение отображение
относ. Ox относ. Oy относ. Ox относ. Oy
Задания к практической работе
Задание. Построить график функции:
1. 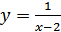 ;
;
2. 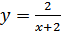 ;
;
3.  ;
;
4. 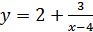 ;
;
5. 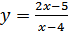 ;
;
6. 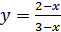 ;
;
7. 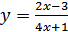 ;
;
8. 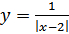 .
.
Контрольные вопросы
1. Каким преобразованием можно получить из графика функции 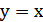 графики функций: а)
графики функций: а) 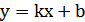 ; б)
; б) 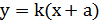 .
.
2. Как зависит расположение графика функции 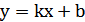 от величины
от величины 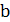 ?
?
3. Функция задана формулой 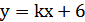 . При каком значении
. При каком значении 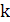 график этой функции параллелен графику функции: а)
график этой функции параллелен графику функции: а) 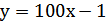 ; б)
; б) 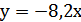 ; в)
; в) 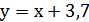 ?
?
Рекомендуемая литература: 1.1, 1.3, 1,4, 2.1.
Практическая работа №26
Теоретический материал
Если точка M движется по окружности радиуса R (рис.26.1) с посто-
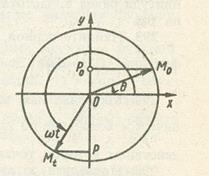 Рисунок 26.1 – Движение точки
Рисунок 26.1 – Движение точки
| янной угловой скоростью 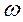 , то проекция P точки M на ось Oy совершает по этой оси колебательное движение по закону: , то проекция P точки M на ось Oy совершает по этой оси колебательное движение по закону: 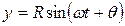 (26.1)
Движение точки P называется простым гармоническим колебанием. Величина R (амплитуда колебания) выражает максимальное отклонение колеблющейся точки P от начала координат; (26.1)
Движение точки P называется простым гармоническим колебанием. Величина R (амплитуда колебания) выражает максимальное отклонение колеблющейся точки P от начала координат; 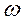 – угловая скорость точки M в радианах в секунду; t – время в секундах, за которое точка M перемещается – угловая скорость точки M в радианах в секунду; t – время в секундах, за которое точка M перемещается
|
При 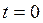 радиус-вектор
радиус-вектор 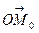 образует с осью Ox угол
образует с осью Ox угол 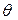 . Через t секунд радиус-вектор повернется на угол
. Через t секунд радиус-вектор повернется на угол 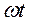 и образует с осью Ox угол
и образует с осью Ox угол 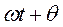 . Следовательно, проекция точки, равномерно движущейся по окружности радиуса R с угловой скоростью
. Следовательно, проекция точки, равномерно движущейся по окружности радиуса R с угловой скоростью 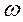 , совершает гармонические колебания с амплитудой R и начальной фазой
, совершает гармонические колебания с амплитудой R и начальной фазой 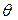 .
.
Время T, в течение которого точка P пройдет через все фазы, а точка M совершит один полный оборот по окружности, называется периодом гармонического колебания, т.е. T есть период функции 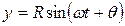 . Так как точка P за время T совершает один полный оборот, т.е. описывает дугу
. Так как точка P за время T совершает один полный оборот, т.е. описывает дугу 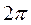 радиан, то за единицу времени она опишет угол
радиан, то за единицу времени она опишет угол 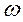 , равный
, равный 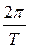 радиан, поэтому угловая скорость:
радиан, поэтому угловая скорость:
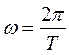 (26.1).
(26.1).
Отсюда следует, что
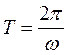 (26.2).
(26.2).
Величина, обратная периоду колебания T , т.е. 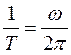 , называется частотой колебания. Частота колебания показывает число колебаний n, совершаемых точкой в секунду:
, называется частотой колебания. Частота колебания показывает число колебаний n, совершаемых точкой в секунду:
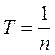 (26.3).
(26.3).
Пример 1. Составить уравнение гармонического колебания, если амплитуда равна 10, период равен 0,5, а начальная фаза равна 1,5.
Решение: по формуле (26.1) находим 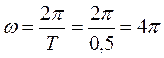 . Подставляя R =10;
. Подставляя R =10;  =1,5;
=1,5; 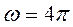 в равенство (26.1), получим
в равенство (26.1), получим 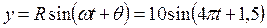 .
.
Ответ: 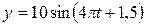 .
.
Пример 2. Найти период, амплитуду и начальную фазу следующих функций:
1) 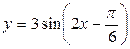 ; ;
| 2) 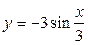 ; ;
| 3) 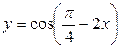
|
Решение: 1) Здесь R=3, 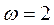 ,
, 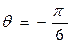 . Период T находим из соотношения (26.3), т.е.
. Период T находим из соотношения (26.3), т.е. 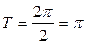 .
.
2) Здесь 
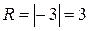 ,
, 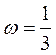 ,
, 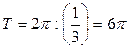 . Для вычисления начальной фазы запишем данную функцию в виде
. Для вычисления начальной фазы запишем данную функцию в виде 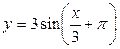 , откуда
, откуда 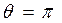 .
.
3) Преобразуем данную функцию следующим образом: 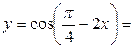
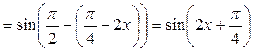 , откуда
, откуда  ,
, 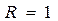 ,
, 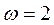 ,
, 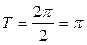 .
.
Задания к практической работе
Задание 1. Составить уравнение гармонического колебания, если амплитуда равна 5, частота колебания равна 3, а начальная фаза равна 0,8.
Задание 2. Найти период, амплитуду и начальную фазу следующих функций 1) 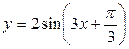 ; 2)
; 2) 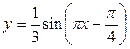 ; 3)
; 3) 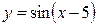 .
.
Задание 3. Материальная точка массы 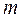 совершает простое гармоническое колебание по закону
совершает простое гармоническое колебание по закону 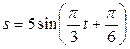 . Найти силу
. Найти силу 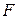 , под действием которой точка совершает это движение в момент
, под действием которой точка совершает это движение в момент 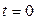 .
.
Задание 4. Привести к виду 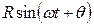 выражения: 1)
выражения: 1) 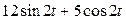 ;
;
2) 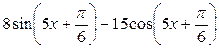 .
.
Задание 5. Найти амплитуду и начальную фазу сумм следующих колебаний: 1) 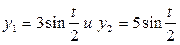 ; 2)
; 2)  ;
;
3) 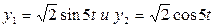 .
.
Контрольные вопросы
1. Назвать закон, по которому проекция точки совершает колебательное движение.
2. Дать определение периода гармонического колебания.
3. Как называется величина обратная периоду колебания?
Рекомендуемая литература: 1.1, 1.3, 1,4, 2.1.
СПИСОК ЛИТЕРАТУРЫ
1. Основная:
1.1 Кремер, Н. Ш. Математика для колледжей : учебное пособие для
СПО / Н. Ш. Кремер, О. Г. Константинова, М. Н. Фридман ; под ред. Н. Ш. Кремера. — 10-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 346 с.
1.2 Богомолов, Н. В. Практические занятия по математике в 2 ч. Часть 1 : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 285 с.
1.3 Богомолов, Н. В. Практические занятия по математике в 2 ч. Часть 2 : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 217 с.
1.4 Богомолов, Н. В. Алгебра и начала анализа : учебное пособие для СПО / Н. В. Богомолов. — М. : Издательство Юрайт, 2018. — 200 с.
1.5 Далингер, В. А. Методика обучения стереометрии посредством решения задач : учебное пособие для СПО / В. А. Далингер. — 2-е изд., испр. и доп. — М. : Издательство Юрайт, 2018. — 370 с.
2. Дополнительная:
2.1 Шипачев, В. С. Математика : учебник и практикум для СПО / В. С. Шипачев ; под ред. А. Н. Тихонова. — 8-е изд., перераб. и доп. — М. : Издательство Юрайт, 2017. — 447 с.
2.2 Кремер, Н. Ш. Теория вероятностей и математическая статистика : учебник и практикум для академического бакалавриата / Н. Ш. Кремер. — 4-е изд., перераб. и доп. — М. : Издательство Юрайт, 2017. — 514 с.
Учебное издание
ОУДп.01 МАТЕМАТИКА: АЛГЕБРА, НАЧАЛА
Дата: 2018-12-28, просмотров: 457.
 .
. .
.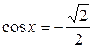 ;
;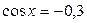 ;
;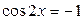 ;
;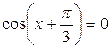 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
;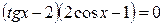 ;
;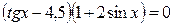 ;
;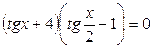 ;
;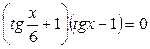 .
.