Цель: формирование навыков нахождения обратных функций, построения их графиков
Вид работы: индивидуальный.
Время выполнения: 2 часа.
Теоретические сведения
Если функция y=f(x) принимает каждое свое значение только при одном значении x, то эту функцию называют обратимой.
Пусть функция y=f(x) монотонна в своей области определения D ( f ). Тогда каждому значению 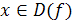 соответствует единственное значение
соответствует единственное значение 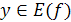 и обратно: каждое значение
и обратно: каждое значение 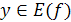 соответствует единственному
соответствует единственному 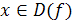 . Значит, в этом случае можно построить новую функцию, определенную на E(f) и такую, что каждому
. Значит, в этом случае можно построить новую функцию, определенную на E(f) и такую, что каждому 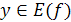 ставится в соответствие
ставится в соответствие 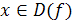 , удовлетворяющее уравнению y=f(x). Эта новая функция называется обратной по отношению к функции y = f ( x ).
, удовлетворяющее уравнению y=f(x). Эта новая функция называется обратной по отношению к функции y = f ( x ).
Для нахождения функции, обратной данной y=f(x), надо выразить х через у: x=g (у), а затем записать полученную функцию в общепринятой форме y = g(x).
Отметим, что если функции y=f(х) и y=g(x) являются взаимно обратными, то область определения функции f совпадает с множеством значений функции g и, наоборот, область определения функции g совпадает с множеством значений функции f, т. e. 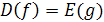 и
и 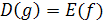 .
.
Графики взаимно обратных функций симметричны относительно прямой у=х (рис. 24.1).
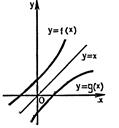
Рисунок 24.1 - Графики взаимно обратных функций
Рассмотрим, например, функцию 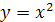 , заданную на промежутке
, заданную на промежутке 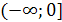 . На этом промежутке функция убывает и принимает все значения из множества [0; +∞). Следовательно, для данной функции существует обратная. Из уравнения
. На этом промежутке функция убывает и принимает все значения из множества [0; +∞). Следовательно, для данной функции существует обратная. Из уравнения 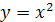 находим
находим 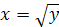 или
или 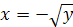 ; так как переменная х может принимать только неположительные значения, то искомая обратная функция имеет вид
; так как переменная х может принимать только неположительные значения, то искомая обратная функция имеет вид 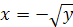 . Поменяв обозначения х на у и у на х, получим формулу
. Поменяв обозначения х на у и у на х, получим формулу 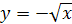 , где
, где 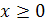 , с помощью которой и задается обратная функция.
, с помощью которой и задается обратная функция.
Если же рассматривать функцию 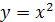 , заданную на промежутке [0; +∞), то обратной для нее служит функция
, заданную на промежутке [0; +∞), то обратной для нее служит функция 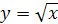 , где
, где 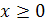 . На рисунке 24.2 изображены график функции
. На рисунке 24.2 изображены график функции 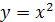 при
при 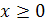 и график обратной ей функции.
и график обратной ей функции.
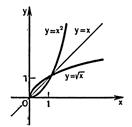
Рисунок 24.2 - График функции 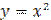 и обратной ей функции
и обратной ей функции
Пример. Задать формулой функцию, обратную f. Построить графики данной и обратной ей функции, если функция f задана формулой:
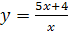 , где
, где 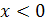 .
.
Решение. Выразив х через у, имеем 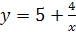 ,
, 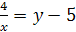 ,
, 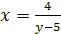 . Заменив х на у, а у на х, получим
. Заменив х на у, а у на х, получим 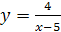 . Найдем область определения обратной функции, она совпадает с множеством значений заданной функции. Этим множеством служит промежуток
. Найдем область определения обратной функции, она совпадает с множеством значений заданной функции. Этим множеством служит промежуток 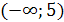 (рис.24.3). Итак,
(рис.24.3). Итак, 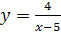 ,
, 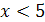 - функция, обратная данной.
- функция, обратная данной.
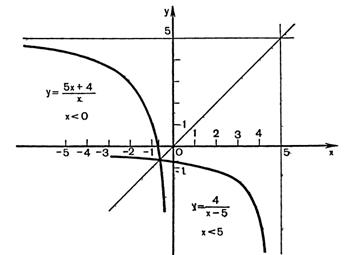
Рисунок 24.3 - Графики обратных функций
Задания к практической работе
Задание 1. Найти функцию, обратную к данной:
1. 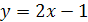 ;
;
2. 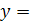 −5x+4;
−5x+4;
3. 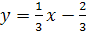 ;
;
4. 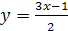 ;
;
5. 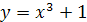 ;
;
6. 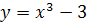 ;
;
7. 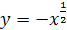 ;
;
8. 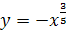 ;
;
9. 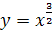 ;
;
10. 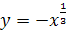 .
.
Задание 2. Найти область определения и множество значений функции, обратной к данной:
1. 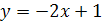 ;
;
2. 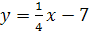 ;
;
3. 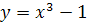 ;
;
4. 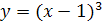 ;
;
5. 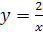 ;
;
6. 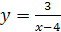 .
.
Задание 3. Функция 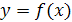 задана графиком (рис. 24.4, а, б, в, г). Построить график функции, обратной к данной.
задана графиком (рис. 24.4, а, б, в, г). Построить график функции, обратной к данной.
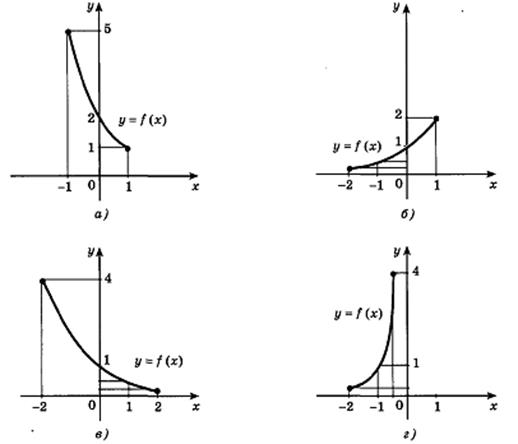
Рисунок 24.4 – Графики функций
Задание 4. На одном рисунке построить график данной функции и функции, обратной к данной; найти область определения и множество значений каждой из них:
1. 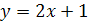 ;
;
2.  ;
;
3. 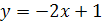 ;
;
4. 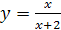 ;
;
5. 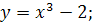
6. 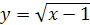 ;
;
7. 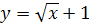 ;
;
8. 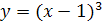 .
.
Контрольные вопросы
1. Дать определение обратной функции.
2. Как определить область определения обратной функции?
3. Как определить множество значений обратной функции?
4. Является ли монотонная функция обратимой?
5. Как можно построить график обратной функции?
Рекомендуемая литература: 1.1, 1.3.
Практическая работа №25
Тема: Преобразования графика функции
Цель: формирование навыков построения графиков функций и выполнения их основных преобразований.
Вид работы: индивидуальный
Время выполнения: 2 часа
Теоретический материал
Если известен график функции 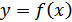 , то с помощью некоторых преобразований плоскости (параллельного переноса, осевой и центральной симметрии и т.п.) можно построить графики более сложных функций.
, то с помощью некоторых преобразований плоскости (параллельного переноса, осевой и центральной симметрии и т.п.) можно построить графики более сложных функций.
1) График функции 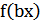 получается сжатием графика
получается сжатием графика 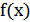 в
в 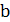 раз к оси
раз к оси 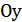 при
при 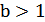 или растяжением в
или растяжением в  раз от этой оси
раз от этой оси 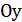 при
при 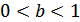 (рис.25.1).
(рис.25.1).
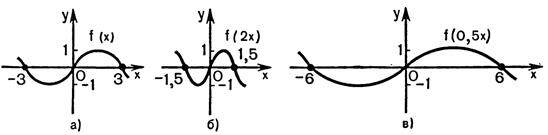
Рисунок 25.1 - Сжатие и растяжение
2) График функции 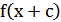 получается параллельным переносом графика
получается параллельным переносом графика 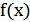 в отрицательном направлении оси
в отрицательном направлении оси 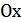 на
на 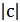 при
при 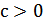 и в положительном направлении на
и в положительном направлении на 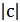 при
при 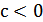 (рис.25.2).
(рис.25.2).
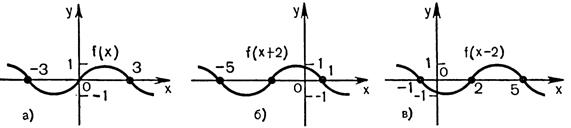
Рисунок 25.2 - Движение вдоль оси Ox
3) График функции 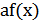 получается растяжением графика
получается растяжением графика 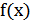 вдоль оси
вдоль оси 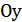 в
в 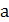 раз при
раз при 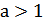 и сжатием вдоль этой оси в
и сжатием вдоль этой оси в  раз при
раз при 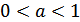 (рис.25.3).
(рис.25.3).
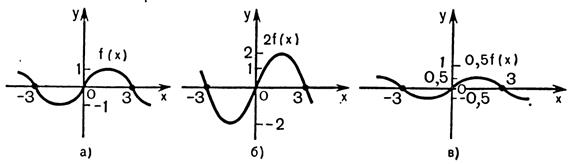
Рисунок 25.3 - Сжатие и растяжение
4) График функции 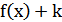 получается параллельным переносом графика
получается параллельным переносом графика 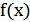 в положительном направлении оси
в положительном направлении оси 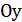 на
на 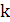 при
при 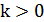 и в отрицательном направлении этой оси на
и в отрицательном направлении этой оси на 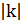 при
при 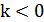 (рис.25.4).
(рис.25.4).
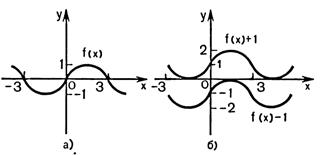
Рисунок 25.4 - Движение вдоль оси Oy
5) График функции 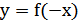 получается симметричным отображением графика
получается симметричным отображением графика 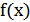 относительно оси
относительно оси 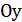 (рис.25.5).
(рис.25.5).
6) График функции 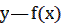 получается симметричным отображением графика
получается симметричным отображением графика 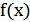 относительно оси
относительно оси 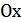 (рис.25.6).
(рис.25.6).
7) График функции 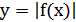 получается из графика функции
получается из графика функции 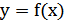 следующим образом: часть графика
следующим образом: часть графика 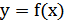 , лежащая над осью
, лежащая над осью 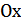 , сохраняется, часть его, лежащая под осью
, сохраняется, часть его, лежащая под осью 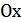 , отображается симметрично относительно оси
, отображается симметрично относительно оси 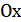 (рис.25.7).
(рис.25.7).
8) График функции 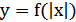 получается из графика функции
получается из графика функции 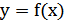 следующим образом: при
следующим образом: при 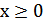 график
график 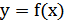 сохраняется, а при
сохраняется, а при 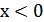 полученная часть графика отображается симметрично относительно оси
полученная часть графика отображается симметрично относительно оси  (рис.25.8).
(рис.25.8).
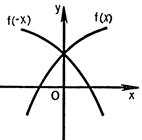
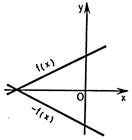
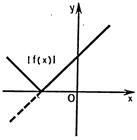
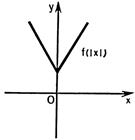
Рисунок 25.5 - Рисунок 25.6 - Рисунок 25.7 - Рисунок 25.8 -
симметричное симметричное симметричное симметричное
отображение отображение отображение отображение
относ. Ox относ. Oy относ. Ox относ. Oy
Задания к практической работе
Задание. Построить график функции:
1. 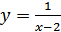 ;
;
2. 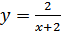 ;
;
3.  ;
;
4. 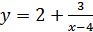 ;
;
5. 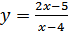 ;
;
6. 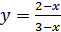 ;
;
7. 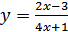 ;
;
8. 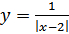 .
.
Контрольные вопросы
1. Каким преобразованием можно получить из графика функции 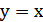 графики функций: а)
графики функций: а) 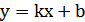 ; б)
; б) 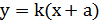 .
.
2. Как зависит расположение графика функции 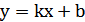 от величины
от величины 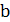 ?
?
3. Функция задана формулой 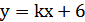 . При каком значении
. При каком значении 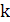 график этой функции параллелен графику функции: а)
график этой функции параллелен графику функции: а) 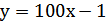 ; б)
; б) 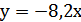 ; в)
; в) 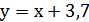 ?
?
Рекомендуемая литература: 1.1, 1.3, 1,4, 2.1.
Практическая работа №26
Дата: 2018-12-28, просмотров: 497.