Цель: формирование навыков построения графиков обратных тригонометрических функций, определения их области определения и множества значений.
Вид работы: индивидуальный.
Время выполнения: 4 часа.
Теоретические сведения
Функция 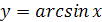
Перечислим основные свойства функции 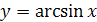 .
.
1) Область определения – отрезок 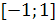 .
.
2) Множество значений – отрезок 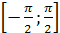 .
.
3) Функция 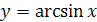 возрастает.
возрастает.
4) Функция 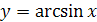 является нечетной, так как
является нечетной, так как 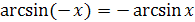 .
.
График функции 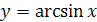 симметричен графику функции
симметричен графику функции 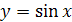 ,
, 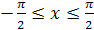 относительно прямой
относительно прямой 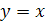 (рис. 22.1).
(рис. 22.1).
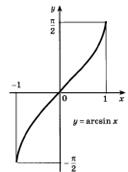
Рисунок 22.1 - График функции 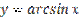
Функция 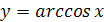
Перечислим основные свойства функции 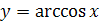 .
.
1) Область определения – отрезок 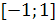 .
.
2) Множество значений – отрезок 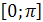 .
.
3) Функция 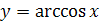 убывает.
убывает.
График функции 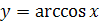 симметричен графику функции
симметричен графику функции 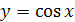 ,
, 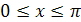 относительно прямой
относительно прямой 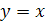 (рис. 22.2).
(рис. 22.2).
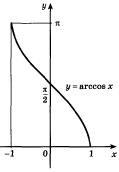
Рис. 22.2 - График функции 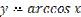
Функция 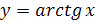
Перечислим основные свойства функции  .
.
1) Область определения – множество 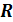 всех действительных чисел.
всех действительных чисел.
2) Множество значений – интервал 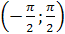 .
.
3) Функция  возрастает.
возрастает.
4) Функция  является нечетной:
является нечетной: 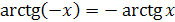 .
.
График функции  получается из графика функции
получается из графика функции 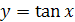 ,
, 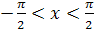 , симметрией относительно прямой
, симметрией относительно прямой 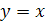 (рис. 22.3).
(рис. 22.3).
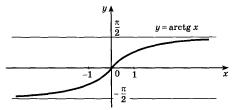
Рисунок 22.3 - График функции 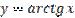
Пример 1. Найти область определения функции 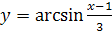 .
.
Решение. Так как функция 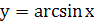 определена при
определена при 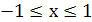 , то функция
, то функция 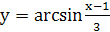 определена для тех значений
определена для тех значений 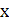 , для которых выполняются неравенства
, для которых выполняются неравенства 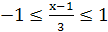 . Отсюда
. Отсюда 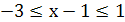 ,
, 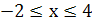 .
.
Пример 2. Решить уравнение 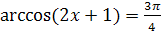 .
.
Решение. Так как 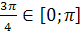 , то по определению арккосинуса числа данное уравнение равносильно уравнению
, то по определению арккосинуса числа данное уравнение равносильно уравнению 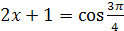 , откуда
, откуда 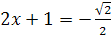 ,
, 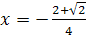 .
.
Задания к практической работе
Задание 1. Найти область определения функции:
1. 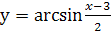 ;
;
2. 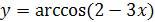 ;
;
3. 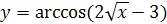 ;
;
4. 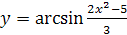 .
.
Задание 2. Доказать, что график функции 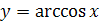 симметричен относительно точки
симметричен относительно точки 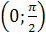 .
.
Задание 3. Решить уравнение:
1. 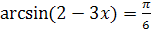 ;
;
2. 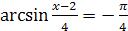 ;
;
3. 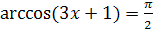 ;
;
4. 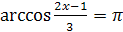 ;
;
5. 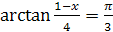 ;
;
6. 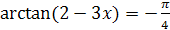 .
.
Контрольные вопросы
1. Дать определение функции 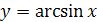 .
.
2. Дать определение функции 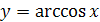 .
.
3. Дать определение функции  .
.
4. Дать определение функции 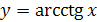 .
.
5. Перечислить свойства обратных тригонометрических функций.
Рекомендуемая литература: 1.1, 1.3, 1.4.
Практическая работа №23
Тема: Примеры зависимостей между переменными в реальных процессах из смежных дисциплин. Построение и чтение графиков функций
Цель: формирование представления о графике функции, способы практического применения графиков функций
Вид работы: индивидуальный.
Время выполнения: 2 часа.
Теоретические сведения
Определение.
1. Функция - это закон, по которому каждому значению элемента x из некоторого множества X ставится в соответствие единственный элемент y из множества Y.
2. Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом, а переменную у - зависимой переменной. Значение у, соответствующее заданному значению х, называют значением функции.
Записывают: у = f (х). Буквой f обозначается данная функция, т. е. функциональная зависимость между переменными х и у; f (х) есть значение функции, соответствующее значению аргумента х. Говорят также, что f (х) есть значение функции в точке х. Все значения, которые принимает независимая переменная, образуют область определения функции. Все значения, которые принимает функция f (х) (при х, принадлежащих области ее определения), образуют область значений функции.
Способы задания функции
Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у = f (х), где f (х) - некоторое выражение с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.
На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента.
График функции.
Пусть функция задана аналитически формулой у = f (х). Если на координатной плоскости отметить все точки, обладающие следующим свойством: абсцисса точки принадлежит области определения функции, а ордината равна соответствующему значению функции, то множество точек (х; f (x)) есть график функции.
На практике для построения графика функции составляют таблицу значений функции при некоторых значениях аргумента, наносят на плоскость соответствующие точки и соединяют полученные точки линией. При этом предполагают, что график функции является плавной линией, а найденные точки достаточно точно показывают ход изменения функции. Преимуществом графического изображения по сравнению с табличным являются его наглядность и легкая обозримость; недостатком - малая степень точности. Большое практическое значение имеет удачный выбор масштабов. По графику можно найти (приблизительно) значение функции и для тех значений аргумента, которые не помещены в таблице.
Пример 1. График описывает движение парусной яхты, которая первую часть пути прошла под парусом. Спустив парус, она продолжила движение.
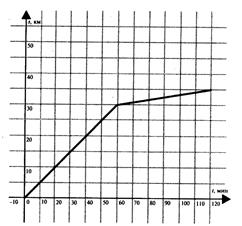 Рисунок 23.1 - Движение яхты
Рисунок 23.1 - Движение яхты
| 1) Найти скорость яхты «под парусом » и «без паруса» (выраженные в км/ч); 2) На каком расстоянии от начала движения находилась яхта через 50 минут, через 2 часа? 3) Сколько времени потребуется яхте на обратный путь, если она будет двигаться с той же скоростью, что и на первом участке «под парусом»? |
Решение: 1) Под парусом яхта прошла 30 км за 60 мин, т.е. за 1 ч., значит её скорость была 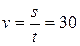 км/ч. Без паруса яхта прошла 5 км за 60 мин, значит её скорость была 5 км/ч.
км/ч. Без паруса яхта прошла 5 км за 60 мин, значит её скорость была 5 км/ч.
Ответ: скорость яхты «под парусом » 30 км/ч и скорость яхты «без паруса» 5 км/ч.
2) На графике найдем точку с абсциссой равной 50. Найдем ординату этой точки. Она равна 25. Получили, что за 50 минут яхта пройдет 25 км. Аналогично, за 120 мин - 35 км.
Ответ: за 50 минут яхта пройдет 25 км, за 120 мин яхта пройдет 35 км.
3) Обратный путь составляет 35 км. Скорость яхты 30 км/ч. Найдем время обратного пути: 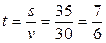 ч, что составляет 1 час 10 минут.
ч, что составляет 1 час 10 минут.
Ответ: 1 ч 10 мин.
Задания к практической работе
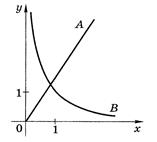 Рисунок 23.2 –
зависимости функций
Рисунок 23.2 –
зависимости функций
| Задание 1. На рисунке схематически изображены графики двух зависимостей: 1) зависимости расстояния, пройденного автомобилем от времени движения при постоянной скорости; 2) зависимости времени движения автомобиля между двумя городами от скорости движения. Какой из графиков является графиком первой зависимости? |
Задание 2. Турист отправился из лагеря к озеру, отдохнул у озера и вер-
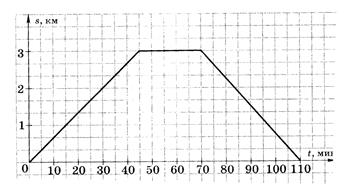
| нулся обратно. На рисунке изображен график движения туриста (по горизонтальной оси откладывается время, по вертикальной – расстояние , на котором находится турист от лагеря ). Найдите скорость туриста на обратном пути, выразив её в км/ч. |
Рисунок 23.3 – Движение туриста
Задание 3. На рисунке изображен график функции  . Из приведенных утверждений выберите верное.
. Из приведенных утверждений выберите верное.
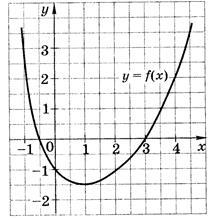
| А. 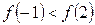 Б. Функция
Б. Функция 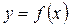 убывает на промежутке убывает на промежутке 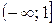 В.
В. 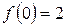 Г. Функция принимает наименьшее значение при
Г. Функция принимает наименьшее значение при 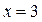
|
Рисунок 23.4 – График функции
Задание 4. Плот плывет по реке. На рисунке изображен график его движе-
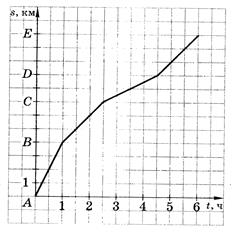
| ния: по горизонтальной оси откладывается время движения t, по вертикальной – расстояние s которое проплыл плот. На каком участке пути скорость течения наибольшая?
|
Рисунок 23.5 – Движение плота
Задание 5. Туристы отправились с турбазы на озеро, провели там 2 ч и вернулись обратно. Какой из графиков описывает зависимость пройденного туристами расстояния от времени, которое они провели в походе?
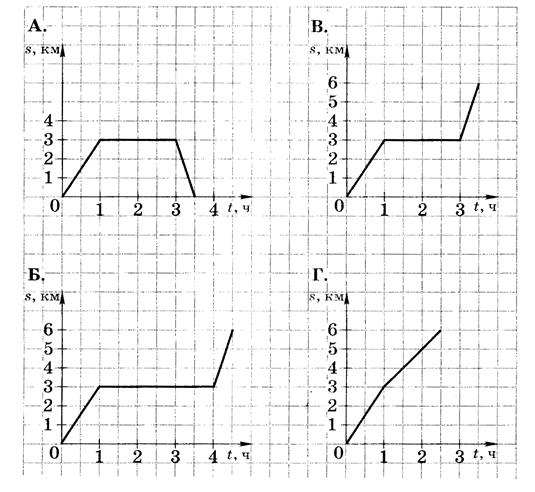
Рисунок 23.6 – Графики зависимостей
Контрольные вопросы
1. Дать определение функции.
2. Назвать способы задания функции.
3. Дать определение графика функции.
Рекомендуемая литература: 1.1, 1.3, 1.4
Практическая работа №24
Дата: 2018-12-28, просмотров: 427.