Цель: формирование навыков решения простейших тригонометрических уравнений.
Вид работы: индивидуальный.
Время выполнения: 4 часа.
Теоретические сведения
Простейшими тригонометрическими уравнениям называют уравнения 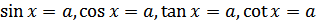 , где
, где 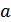 - данное число.
- данное число.
Решить простейшее тригонометрическое уравнение – значит найти множество всех значений аргумента (дуг или углов), при которых данная тригонометрическая функция принимает заданное значение 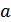 .
.
Формула для корней уравнения 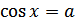 , где
, где 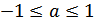 , имеет вид:
, имеет вид:
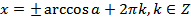 . (20.1)
. (20.1)
Частные случаи:
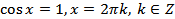 ; (20.2)
; (20.2)
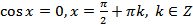 ; (20.3)
; (20.3)
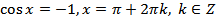 . (20.4)
. (20.4)
Формула для корней уравнения 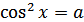 , где
, где 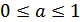 , имеет вид:
, имеет вид:
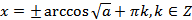 . (20.5)
. (20.5)
Формула для корней уравнения 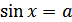 , где
, где 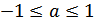 , имеет вид:
, имеет вид:
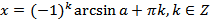 . (20.6)
. (20.6)
Частные случаи:
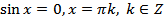 ; (20.7)
; (20.7)
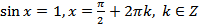 ; (20.8)
; (20.8)
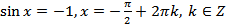 . (20.9)
. (20.9)
Формула для корней уравнения 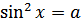 , где
, где 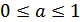 , имеет вид:
, имеет вид:
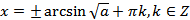 . (20.10)
. (20.10)
Формула для корней уравнения 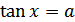 , имеет вид:
, имеет вид:
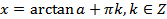 . (20.11)
. (20.11)
Частные случаи:
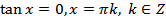 ; (20.12)
; (20.12)
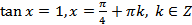 ; (20.13)
; (20.13)
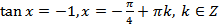 . (20.14)
. (20.14)
Формула для корней уравнения 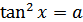 , где
, где 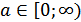 , имеет вид:
, имеет вид:
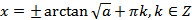 . (20.15)
. (20.15)
Пример 1. Решить уравнения: 1) 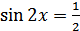 ; 2)
; 2) 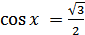 ;
;
3) 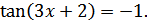
Решение. 1) 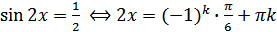 , отсюда следует, что множество корней данного уравнения имеет вид
, отсюда следует, что множество корней данного уравнения имеет вид 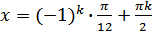 .
.
2) Так как 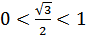 и
и 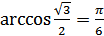 , то
, то 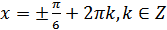
3) 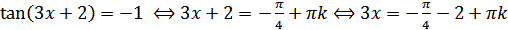 . Тогда множество корней уравнения имеет вид
. Тогда множество корней уравнения имеет вид 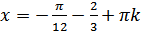 .
.
Пример 2. Решить уравнение 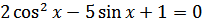 .
.
Решение. Заменяя 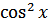 на
на 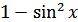 , получаем
, получаем 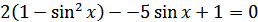 или
или 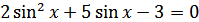 .
.
Обозначая 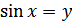 , получаем
, получаем 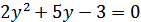 , откуда
, откуда 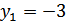 ,
, 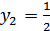 .
.
1) 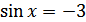 - уравнение не имеет корней, так как
- уравнение не имеет корней, так как 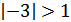 ;
;
2) 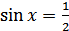 ,
, 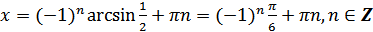 .
.
Таким образом, 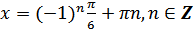 .
.
Пример 3. Решить уравнение 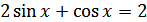 .
.
Решение. Используя формулы 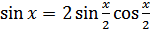 ,
, 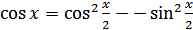 и записывая правую часть уравнения в виде
и записывая правую часть уравнения в виде 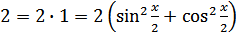 , получаем
, получаем
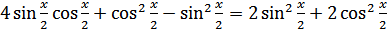 ,
, 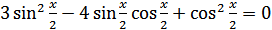 .
.
Поделив это уравнение на 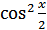 , получим равносильное уравнение
, получим равносильное уравнение 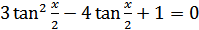 . Обозначая
. Обозначая 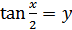 , получим уравнение
, получим уравнение 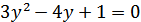 , откуда
, откуда 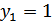 ,
, 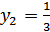 .
.
1) 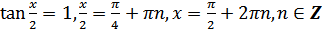 ;
;
2) 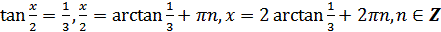 .
.
Задания к практической работе
Задание 1. Решить уравнения:
1. 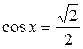 ; ;
| 2. | 3. 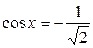 ; ;
| |
4. 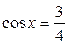 ; ;
| 5. | 6. 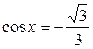 ; ;
| |
7. 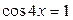 ; ;
| 8. | 9. 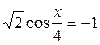 ; ;
| |
10. 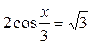 ; ;
| 11. | 12. 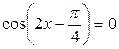 ; ;
| |
| 13. | 14. | ||
| 15. | 16. | ||
| 17. | 18. | ||
| 19. | 20. | ||
| 21. | 22. | ||
Задание 2. Найти все корни уравнения 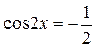 на отрезке
на отрезке 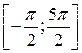 .
.
Задание 3. Решить уравнение:
1. 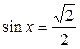 ; ;
| 2. | 3. 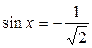 ; ;
| |
4. 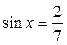 ; ;
| 5. | 6. 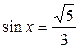 ; ;
| |
7. 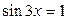 ; ;
| 8. | 9. 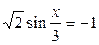 ; ;
| |
10. 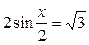 ; ;
| 11. | 12. 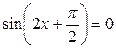 ; ;
| |
| 13. | 14. | ||
| 15. | 16. | ||
| 17. | 18. | ||
| 19. | 20. | ||
| 21. | 22. | ||
Задание 4. Найти все корни уравнения 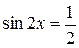 на отрезке
на отрезке 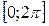 .
.
Задание 5. Решить уравнение:
1. 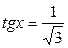 ; ;
| 2. | 3. 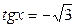 ; ;
| |
4. 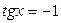 ; ;
| 5. | 6. 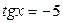 ; ;
| |
7.  ; ;
| 8. | 9. 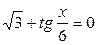 ; ;
| |
| 10. | 11. | ||
| 12. | 13. | ||
| 14. | 15. | ||
Задание 6. Найти наименьший положительный и наибольший отрицательный корни уравнения 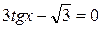 .
.
Контрольные вопросы
1. Какие уравнения называются тригонометрическими?
2. Что называется корнем тригонометрического уравнения?
3. По каким формулам находят решения простейших тригонометрических уравнений?
Рекомендуемая литература: 1.1, 1.3, 1.4.
Практическая работа №21
Тема: Простейшие тригонометрические неравенства
Цель: формирование навыков решения простейших тригонометрических неравенств.
Вид работы: индивидуальный.
Время выполнения: 4 часа.
Теоретические сведения
Пример 1. Решить неравенство: 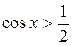 .
.
Решение. По определению 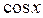 – это абсцисса точки единичной окружности. Чтобы решить неравенство
– это абсцисса точки единичной окружности. Чтобы решить неравенство 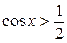 , нужно выяснить, какие точки единичной окружности имеют абсциссу, большую
, нужно выяснить, какие точки единичной окружности имеют абсциссу, большую 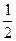 .
.
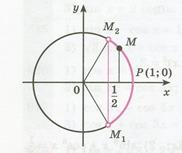 Рисунок 21.1 - Решение неравенства
Рисунок 21.1 - Решение неравенства 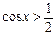
| Абсциссу, равную 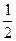 , имеют две точки единичной окружности , имеют две точки единичной окружности 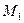 и и 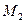 (рис. 21.1) . Точка
(рис. 21.1) . Точка 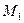 получается поворотом точки получается поворотом точки 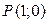 на угол на угол 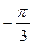 , а также на углы , а также на углы 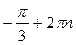 , где , где 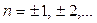 . Точка . Точка 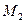 получается поворотом точки получается поворотом точки 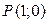 на угол на угол 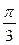 , а также на углы , а также на углы 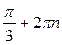 , где , где 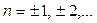 . .
|
Абсциссу, большую 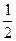 , имеют все точки
, имеют все точки  дуги единичной окружности, лежащие правее прямой
дуги единичной окружности, лежащие правее прямой  . Таким образом, решениями неравенства
. Таким образом, решениями неравенства 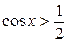 являются все числа
являются все числа 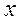 из промежутка
из промежутка 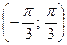 . Все решения данного неравенства – множество интервалов:
. Все решения данного неравенства – множество интервалов: 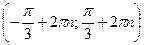 ,
, 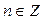 .
.
Пример 2. Решить неравенство: 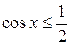 .
.
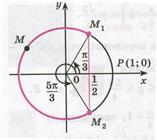 Рисунок 21.2 - Решение неравенства
Рисунок 21.2 - Решение неравенства 
| Решение. Абсциссу, не большую 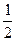 , имеют все точки дуги , имеют все точки дуги 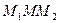 единичной окружности (рис. 2). Поэтому решениями неравенства единичной окружности (рис. 2). Поэтому решениями неравенства 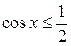 являются числа являются числа 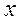 , которые принадлежат отрезку , которые принадлежат отрезку 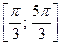 . Все решения данного неравенства – множе- . Все решения данного неравенства – множе-
|
ство отрезков: 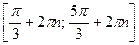 ,
, 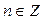 .
.
Пример 3. Решить неравенство: 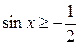 .
.
Решение. Ординату, не меньшую 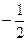 , имеют все точки дуги
, имеют все точки дуги 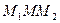 единичной окружности (рис. 21.3).
единичной окружности (рис. 21.3).
 Рисунок 21.3 - Решение
неравенства
Рисунок 21.3 - Решение
неравенства 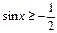
| Поэтому решениями неравенства 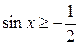 являются числа являются числа 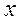 , которые принадлежат отрезку , которые принадлежат отрезку 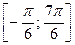 . Все решения данного неравенства – множество отрезков: . Все решения данного неравенства – множество отрезков: 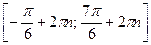 , , 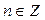 . .
|
Отметим, что все точки окружности, лежащие ниже прямой 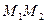 , имеют ординату, меньшую
, имеют ординату, меньшую 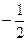 (рис. 21.3). Поэтому все числа
(рис. 21.3). Поэтому все числа 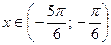 являются решениями неравенства
являются решениями неравенства 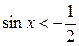 .
.
Все решения этого неравенства – интервалы: 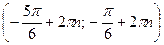 ,
, 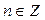 .
.
Пример 4. Решить неравенство: 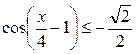 .
.
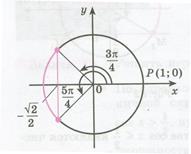 Рисунок 21.4 - Решение неравенства
Рисунок 21.4 - Решение неравенства 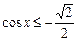
| Решение. Обозначим 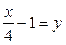 . Решая неравенство . Решая неравенство 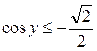 (рис. 21.4), находим (рис. 21.4), находим 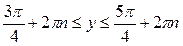 , , 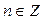 . Заменяя . Заменяя 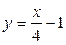 , получаем: , получаем: 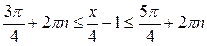 , ,
|
откуда 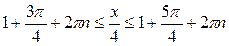
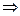
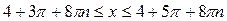 ,
, 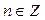 .
.
Ответ: 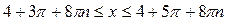 ,
, 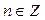 .
.
Задания к практической работе
Задание 1. Решить неравенство:
1. 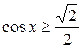 ; ;
| 2. 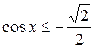 ; ;
| 3. 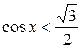 ; ;
|
4. 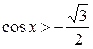 ; ;
| 5. 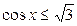 ; ;
| 6. 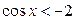 ; ;
|
7. 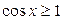 ; ;
| 8. 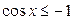 ; ;
| 9. 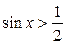 ; ;
|
10.  ; ;
| 11. 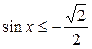
| 12. 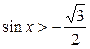
|
13. 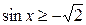 ; ;
| 14. 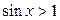 ; ;
| 15. 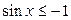 ; ;
|
16. 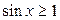 ; ;
| 17. 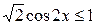 ; ;
| 18. 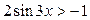 ; ;
|
19. 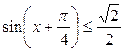 ; ;
| 20. 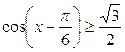 ; ;
| 21. 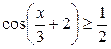 . .
|
Контрольные вопросы
1. Какие неравенства называются тригонометрическими?
2. Какими способами можно решить простейшее тригонометрическое неравенство?
Рекомендуемая литература: 1.1, 1.3, 1.4.
Практическая работа №22
Дата: 2018-12-28, просмотров: 385.
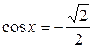 ;
;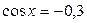 ;
;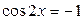 ;
;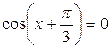 ;
;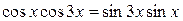 ;
;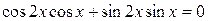 ;
;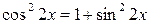 ;
;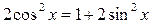 ;
;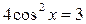 ;
;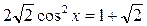 ;
;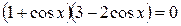 ;
;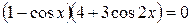 ;
;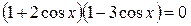 ;
;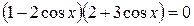 .
.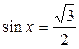 ;
;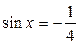 ;
;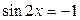 ;
;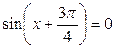 ;
;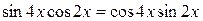 ;
;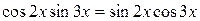 ;
;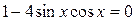 ;
; ;
;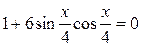 ;
;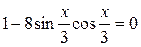 ;
;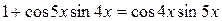 ;
;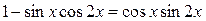 ;
;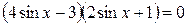 ;
;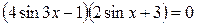 .
.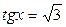 ;
;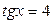 ;
;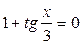 ;
;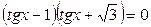 ;
;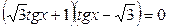 ;
;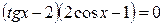 ;
;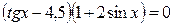 ;
;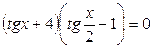 ;
;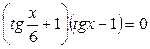 .
.