- сила упругости
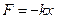
где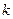 
- коэффициент упругости ( в случае пружины – жёсткости); 
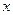-абсолютная деформация;
- сила тяжести
;
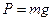- сила гравитационного взаимодействия
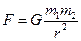
где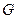 
- гравитационная постоянная; 
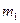и 
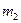- массы взаимодействующих тел; 
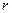- расстояние между телами. Силу можно выразить через напряженность гравитационного поля 
:
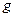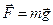
(тела рассматриваются как материальные точки). В случае гравитационного взаимодействия силу можно выразить также через напряжённость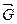 
гравитационного поля.
- сила трения (скольжения)
F=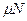 
,
где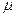 
- коэффициент трения; N - сила нормального давления.
Закон сохранения импульса.
,
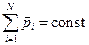или для двух тел (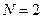 
)
,
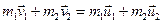где 
v 
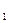и v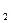 
- скорости тел в момент времени, принятый за
начальны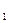й; u и u 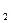- скорости тех же тел в момент времени, принятый за конечный.
Кинетическая энергия тела, движущегося поступательно:
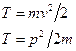
Потенциальная энергия:
- упруго деформированной пружины
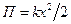
где k - жёсткость пружины; x - абсолютная деформация;
- гравитационного взаимодействия
,
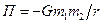где 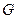- гравитационная постоянная; m 
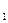и m 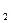- массы взаимодействующих тел; r - расстояние между ними (тела рассматриваются как материальные точки);
- тела, находящегося в однородном поле силы тяжести,
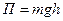
где g - ускорение свободного падения; h - высота тела над уровнем, принятым за нулевой (формула справедлива при условии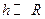 
, где R - радиус Земли).
Закон сохранения механической энергии
E = T +П=const.
Работа A, совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки:
ΣA =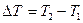 
.
Основное уравнение динамики вращательного движения относительно неподвижной оси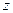 
:
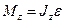
где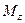 
- результирующий момент внешних сил относительно
оси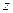 
, действующих на тело; ε - угловое ускорение; 
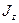- момент инерции тела относительно оси вращения.
Моменты инерции некоторых тел массой m относительно оси z, проходящей через центр масс:
- стержня длиной l относительно оси, перпендикулярной стержню
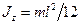
- обруча (тонкостенного цилиндра) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра)
,
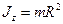где R - радиус обруча (цилиндра);
- диска радиусом R относительно оси, перпендикулярной плоскости диска,
.
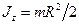- шара радиусом R относительно оси, проходящей через центр массы
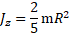
Проекция на ось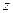 
момента импульса тела, вращающегося относительно неподвижной оси 
:
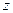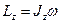
где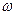 
- угловая скорость тела.
Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси :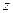
.
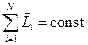Кинетическая энергия тела, вращающегося вокруг неподвижной оси :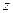
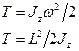
ЗАДАЧИ.
1. Точка движется по окружности R=1.2 м. Уравнение движения точки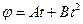 
, где А=0.5 рад/с; В=0.2 рад/с2. Определить тангенциальное, нормальное и полное ускорение точки в момент времени t=4 с.
2. Определить скорость и полное ускорение точки в момент времени t=2 с, если она движется по окружности R=1 м согласно уравнению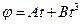 
, где А=8 рад/с; В=-1рад/с3.
3. По прямой движутся две материальные точки согласно уравнениям: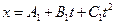 
и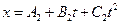 
, где А1=10 м; В1=1 м/с; С1= -2 м/с2; А2=3 м; В2=2 м/с; С2= 0.2 м/с2. В какой момент времени скорости точек будут одинаковыми? Найти ускорения этих точек в момент времени t=3с.
4. Определить полное ускорение в момент времени t=3с точки, находящейся на ободе колеса радиусом 0.5 м, движущейся согласно уравнения 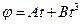, где А=2 с–1, В=0.2 с–3.
5. Диск радиусом 0.5 м вращается согласно уравнению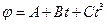 
, где А=3, В= -1 с–1, С=0.1 с–3. Определить тангенциальное, нормальное и полное ускорения точек на окружности диска в момент времени t=10 c.
6. С высоты 2 м на стальную плиту свободно падает шарик массой 200 г и подпрыгивает на высоту 0.5 м.Определить импульс, полученный шариком при ударе.
7. При горизонтальном полете со скоростью 250 м/с снаряд массой 8 кг разорвался на две части. Большая часть снаряда массой 6 кг получила скорость 400 м/с в направлении движения снаряда. Определить величину и направление скорости меньшей части снаряда.
8. Платформа с песком общей массой 2 т стоит на рельсах. В песок попадает снаряд массой 8 кг и застревает в нем. Определить с какой скоростью начнет двигаться платформа, если скорость снаряда 450 м/с, а ее направление – сверху вниз под углом 450 к горизонту.
9. Определить импульс, полученный стенкой при ударе о нее шарика массой 300 г со скоростью 8 м/с под углом 600 к поверхности стенки. Удар считать упругим.
10. На полу стоит тележка в виде длинной доски. На одном конце тележки стоит человек массой 60 кг. Масса тележки – 20 кг. С какой скоростью будет двигаться тележка, если человек будет двигаться по ней со скоростью (относительно тележки) 1 м/с. Трением тележки о пол пренебрегаем.
11. Определить к.п.д. удара тела массой 0.5 т, падающего на сваю массой 120 кг. Полезной считать энергию, затраченную на вбивание сваи.
12. Вагон массой 35 т движется на стенку со скоростью 0.2 м/с. При полном торможении вагона буферные пружины сжимаются на 12 см.Определить максимальную силу сжатия пружин и продолжительность торможения.
13. Лодка длиной 3 м и массой 120 кг стоит на воде. На носу и корме находятся два рыбака массой 60 и 90 кг. На сколько сместится лодка, если рыбаки поменяются местами?
14. На сколько переместится относительно берега лодка длиной 3 м и массой 200 кг, если стоящий на корме человек массой 80 кг переместится на нос лодки?
15. С наклонной плоскости высотой 3 м соскальзывает без трения тело массой 0.5 кг. Определить изменение импульса тела.
16. На обод маховика диаметром 60 см намотан шнур, к концу которого привязан груз массой 2 кг. Определить момент инерции маховика, если он, вращаясь равноускоренно под действием груза, за 3 секунды приобрел скорость 9 рад/сек.
17. Стержень вращается вокруг оси, проходящей через его середину согласно уравнению 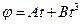, где А=8 м/с; В= -1 м/с3.Определить вращающий момент, действующий на маховик через 2 сек. после начала вращения, если момент инерции стержня равен 4.8×10-2 кг×м2.
18. По горизонтальной поверхности катится диск со скоростью 8 м/с. Определить коэффициент трения, если диск предоставленный самому себе, остановился, пройдя 18 м.
19. Определить момент силы, приложенной к диску, вращающемуся с частотой 12 с–1, если диск остановился через 8 сек. Диск обладает массой 6 кг и диаметром 30 см.
20. Диск массой 0.4 кг вращается под действием силы натяжения нити, к концам которой привязаны грузы массой 0.3 и 0.7 кг. Определить силы натяжения нити по обе стороны диска.
21. На краю платформы в виде диска, вращающегося по инерции вокруг вертикальной оси с частотой 8 мин–1, стоит человек массой 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой 10 мин–1. Определить массу платформы. Момент инерции человека рассчитать как для материальной точки.
22. Определить напряженность гравитационного поля Земли на высоте 1000 км. Считать известными радиус Земли и ускорение свободного падения на ее поверхности.
23. Из бесконечности на поверхность Земли падает метеорит массой 30 кг. Определить работу сил гравитации. Считать известными радиус Земли и ускорение свободного падения на ее поверхности.
24. С поверхности Земли вертикально вверх пущена ракета со скоростью 5 км/с. На какую высоту она поднимется?
25. Спутник движется вокруг Земли на высоте 520 км. Определить период обращения спутника. Считать известными радиус Земли и ускорение свободного падения на ее поверхности.
26. Определить угловую скорость обращения спутника Земли на высоте 1000 км, а также его линейную скорость. Считать известными радиус Земли и ускорение свободного падения на ее поверхности.
27. На краю скамьи Жуковского диаметром 0.8 м и массой 6 кг стоит человек массой 60 кг. С какой угловой скоростью начнет вращаться скамья, если человек поймает мяч массой 0.5 кг, летящий горизонтально со скоростью 5 м/с на расстоянии 0.4 м от оси вращения?
28. Платформа в виде диска диаметром 3 м и массой 180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью будет вращаться платформа, если человек массой 70 кг пойдет по ее краю со скоростью 1.8 м/с относительно платформы?
29. Платформа в виде диска массой 280 кг может вращаться вокруг вертикальной оси. На какой угол повернется платформа, если человек массой 80 кг пойдет по краю платформы и сделает полный оборот относительно платформы? Момент инерции человека рассчитать как для материальной точки.
30. Шарик массой 60 г на нити длиной 1.2 м вращается с частотой 2 с–1 вокруг вертикальной оси. На какой угол отклонится от вертикальной оси нить с шариком?
31. Определить возвращающую силу, действующую на тело массой 20 г в момент времени 0.2 с. Тело совершает гармонические колебания согласно уравнению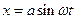 
, где А=15 см и ω=4π с–1.
32. Определить период колебаний стержня длиной 30 см вокруг горизонтальной оси, проходящей через конец стержня.
33. Определить частоту колебаний диска радиусом 20 см вокруг горизонтальной оси, проходящей через середину радиуса диска.
34. Определить период гармонических колебаний диска вокруг горизонтальной оси проходящей через образующую диска.
35. Найти максимальную кинетическую энергию материальной точки массой 2 г, совершающей гармонические колебания с амплитудой 4 см и частотой 5 Гц.
35. Какую разность фаз будут иметь колебания, находящиеся от источника на расстоянии соответственно 10 и 16 см. Период колебаний равен 0.04 сек и скорость распространения колебаний – 300 м/с.
37. Найти разность фаз колебаний в двух точках, отстоящих друг от друга на расстоянии 2 м. Длина волны равна 1 м.
38. Смещение от положения равновесия точки, находящейся на расстоянии 4 см от источника в момент времени Т/6 равна половине амплитуды. Найти длину бегущей волны.
39. Две точки находятся на прямой, вдоль которой распространяется волна со скоростью 10 м/с. Период колебаний равен 0.2 сек., расстояние между точками равно 1 м. Найти разность фаз колебаний в этих точках.
40. Определить скорость распространения упругой волны, если разность фаз колебаний в двух точках, отстоящих друг от друга на 15 см, равна π/2. Частота колебаний равна 25 Гц.
41. Модуль ускорения свободного падения вблизи поверхности астероида равен 0,05 м/с2. Чему будет равен модуль ускорения свободного падения вблизи поверхности другого астероида, объём которого в 8 раз больше? Оба астероида однородные, сферические и состоят из железа. Ответ выразите в м/с2.
42. Два спортсмена разной массы на одинаковых автомобилях, движущихся со скоростью V=20 м/c и U= 25 м/c стали тормозить, заблокировав колеса. Каково отношение тормозных путей их автомобилей при одинаковом коэффициенте трения колес о землю?
43. Санки массой 5 кг скользят по горизонтальной дороге. Сила трения скольжения их полозьев о дорогу 6 Н. Каков коэффициент трения скольжения саночных полозьев о дорогу? Ускорения свободного падения считать равным 10 м/с2.
44. Два искусственных спутника Земли массой m=100 kg и M=300kg обращаются по круговым орбитам одинакового радиуса. Чему равно отношение скоростей этих спутников ?
45. Модуль ускорения свободного падения вблизи поверхности астероида равен 0,2 м/с2. Чему будет равен модуль ускорения свободного падения вблизи поверхности другого астероида, объём которого в 8 раз меньше? Оба астероида однородные, сферические и состоят из железа. Ответ выразите в м/с2.
46. Механическая энергия системы изменилась от величины 5 Дж до величины –3 (минус 3) Дж. Это означает, что на данную механическую систему действовали внешние силы. Какова работа этих сил?
47. Легковой автомобиль и грузовик движутся со скоростями V=20 m/c и U= 25 m/c соответственно. Масса грузовика M=3000kg. Какова масса легкового автомобиля, если импульс грузовика больше импульса легкового автомобиля на 15000 кг·м/с?
48. Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние 5 м, расстояние тела от поверхности Земли при этом увеличивается на 3 м. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила трения? Ускорение свободного падения равно 10 м/с2 коэффициент трения 0.3.
49. В инерциальной системе отсчёта тело массой 2 кг движется по прямой в одном направлении под действием постоянной силы, равной 3 Н. На сколько увеличится импульс тела за 5 с движения?
50. Какую мощность развивает двигатель подъемного механизма крана, если он равномерно поднимает плиту массой 600 кг на высоту 4 м за 3 с? (Ответ дайте в кВт.) Ускорение свободного падения принять равным 10 м/с2.
51. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 10 Н*с Каков модуль силы?
52. Тело свободно падает без начальной скорости. Изменение модуля импульса этого тела за промежуток времени 2 с равно 10 кг·м/с. Чему равна масса тела? Сопротивлением воздуха можно пренебречь.
53. Шарик массой 200 г падает с высоты 20 м с начальной скоростью, равной нулю. Какова его кинетическая энергия в момент перед ударом о землю, если потеря энергии за счёт сопротивления воздуха составила 4 Дж? (Ответ дайте в джоулях.) Ускорение свободного падения принять равным 10 м/с2.
54. На расстоянии 400 м от наблюдателя рабочие вбивают сваи с помощью копра. Каково время между видимым ударом молота о сваю и звуком удара, услышанным наблюдателем? Скорость звука в воздухе 330 м/с .
55. Для экспериментального определения скорости звука ученик встал на расстоянии 30 м от стены и хлопнул в ладоши. В момент хлопка включился электронный секундомер, который выключился отражённым звуком. Время, отмеченное секундомером, равно 0,18 с. Какова скорость звука, определённая учеником?
56. Какова частота колебаний звуковых волн в среде, если скорость звука в среде 1000м/с а длина волны 10 см?
57. Звуковой сигнал, отразившись от препятствия, вернулся обратно к источнику через 5 с после его испускания. Каково расстояние от источника до препятствия, если скорость звука в воздухе 340 м/с?
58. Скорость звука в воде 1,5 км/с. Чему равна длина звуковой волны, распространяющейся в воде, при частоте звука 3 кГц?
59. Гидроакустик, находящийся на корабле, переговаривается по рации с матросом, находящимся на лодке. Во время разговора матрос наносит удар гаечным ключом по корпусу своей лодки. Звук от этого удара гидроакустик сначала слышит через рацию, а через 10 секунд — через свою гидроакустическую аппаратуру. Считая, что второй звук распространяется в воде со скоростью 1500 м/с, найдите расстояние между кораблём и лодкой. Ответ приведите в километрах.
60. Гидроакустик, находящийся на корабле, переговаривается по рации с матросом, находящимся на лодке. Расстояние между кораблем и лодкой составляет 7,5 км. Во время разговора матрос наносит удар гаечным ключом по корпусу своей лодки. Звук от этого удара гидроакустик сначала слышит через рацию, а затем — через свою гидроакустическую аппаратуру. Считая, что второй звук распространяется в воде со скоростью 1500 м/с, найдите время между ударами, которые слышит гидроакустик.
Дата: 2018-12-28, просмотров: 447.
