Ф И З И К А
Учебное пособие:
Методические материалы и указания к выполнению контрольных работ
для студентов заочной формы обучения
Королев, 2017
А.Д.Сабо С.Е., Мацнев Н.П. Физика. Учебное пособие: Методические материалы и указания к выполнению контрольных работ для студентов заочной формы обучения. Королев:, 2017.- 83 с.
Рецензент: д.т.н., профессор Захаров Е.Н.
Методические рекомендации и указания составлены в соответствии с требованиями Федерального государственного образовательного стандарта высшего профессионального образования по специальностям 24.05.01 и направлениям подготовки 15.03.05, 15.03.06, 27.03.02, 27.03.04, 09.03.02, 09.03.03, 01.03.02.
Введение.
1. За время изучения курса общей физики студент–заочник должен представить на кафедру контрольные работы.
2. Контрольные задания выдаются студентам лектором потока.
3. Контрольные работы необходимо выполнять чернилами в школьной тетради, на обложке которой привести сведения по следующему образцу:
Контрольная работа по физике № __
Студент – Киселев А.В.
Группа – УТС–17
Шифр – (номер зачетной книжки).
4. Условия задач в контрольной работе надо переписать полностью без сокращений. Для замечаний преподавателя на страницах тетради оставлять поля.
5. В конце контрольной работы указать, каким учебником или учебным пособием студент пользовался при изучении физики (название учебника, автор, год издания). Это делается для того, чтобы рецензент в случае необходимости мог указать, что следует студенту изучить для завершения контрольной работы.
6. Если контрольная работа при рецензировании не зачтена, студент обязан представить ее на повторную рецензию, включив в нее те задачи, решения которых оказались неверными. Повторную работу необходимо представить вместе с не зачтенной работой.
7. Зачтенные контрольные работы предъявляются экзаменатору. Студент должен быть готов, во время экзамена (зачета) дать пояснения по существу решения задач, входящих в контрольные работы.
8. Решения задач следует сопровождать краткими, но исчерпывающими пояснениями. В тех случаях, когда возможно, дать рисунок, схему.
9. Обозначения физических величин в условии задачи, на рисунке и в ходе решения должны быть одинаковыми.
10. Решать задачу надо в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин.
11. После получения расчетной формулы для проверки правильности ее следует подставить в правую часть формулы вместо символов величин обозначения единиц этих величин, произвести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине. Если такого соответствия нет, то это означает, что задача решена неверно.
12. Числовые значения величин при подстановке их в расчетную формулу следует выражать только в единицах СИ. В виде исключения допускается выражать в любых, но одинаковых единицах числовые значения однородных величин, стоящих в числителе и знаменателе дроби и имеющих одинаковые степени.
Все необходимы для решения задачи значения приведены в задаче и приложениях к данному задачнику.
13. При подстановке в расчетную формулу, а также при записи ответа числовые значения величин следует записывать как произведение десятичной дроби с одной значащей цифрой перед запятой на соответствующую степень десяти. Например, вместо 0,00129 кг записать 1,29*10-3 кг т.п.
14. Вычисления по расчетной формуле надо проводить с соблюдением правил приближенных вычислений (см."Задачник по физике" А. Г. Чертов, А.А.Воробьев «Приложение о приближенных вычислениях».) Как правило, окончательный ответ следует записывать с тремя значащими цифрами. Это относится и к случаю, когда результат получен с применением калькулятора.
Механика
Основные формулы.
Кинематическое уравнение движения материальной точки (центра массы твёрдого тела) вдоль оси 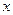 :
:
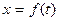
где 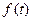 –некоторая функция времени.
–некоторая функция времени.
Проекция средней скорости на ось 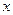 :
:
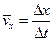
Средняя скорость движения:
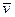 =
= 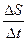
где 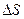 - путь, пройденный точкой за интервал времени
- путь, пройденный точкой за интервал времени 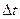 .
.
Путь 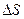 , в отличие от разности координат
, в отличие от разности координат 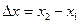 , не может убывать и принимать отрицательные значения, т.е.
, не может убывать и принимать отрицательные значения, т.е. 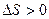 .
.
Проекция мгновенной скорости на ось 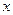 :
:
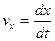
Проекция среднего ускорения на ось 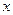 :
:
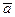 =
= 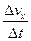
Проекция мгновенного ускорения на ось 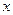 :
:
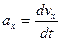
Кинематическое уравнение движения материальной точки по окружности ( 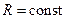 ):
):
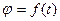 ,
,
Модуль угловой скорости:
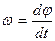
Модуль углового ускорения:
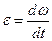
Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:
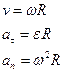
где 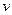 - модуль линейной скорости;
- модуль линейной скорости; 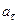 и
и 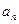 - модули тангенциального и нормального ускорений;
- модули тангенциального и нормального ускорений; 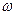 – модуль угловой скорости;
– модуль угловой скорости; 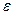 - модуль углового ускорения; R- радиус окружности.
- модуль углового ускорения; R- радиус окружности.
Модуль полного ускорения:
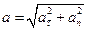 или
или 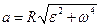
Угол между полным a и нормальным a 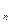 ускорениями:
ускорениями:
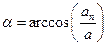
Кинематическое уравнение гармонических колебаний материальной точки:
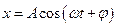
где 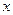 - смещение; A– амплитуда колебаний;
- смещение; A– амплитуда колебаний; 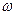 - угловая или циклическая частота;
- угловая или циклическая частота; 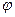 -начальная фаза.
-начальная фаза.
Скорость и ускорение материальной точки, совершающей гармонические колебания:
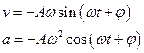
Сложение гармонических колебаний одного направления и одинаковой частоты:
- амплитуда результирующего колебания
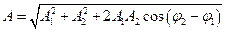
- начальная фаза результирующего колебания
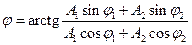
Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях:
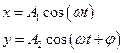
a) 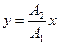 если разность фаз
если разность фаз 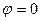 ;
;
б) 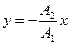 если разность фаз
если разность фаз 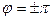 ;
;
в) 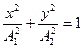 если разность фаз
если разность фаз 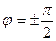
Уравнение плоской бегущей волны:

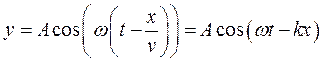
где 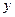 - смещение любой из точек среды с координатой
- смещение любой из точек среды с координатой 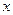 в момент
в момент 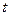 ;
; 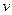 - скорость распространения колебаний в среде,
- скорость распространения колебаний в среде, 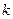 – волновое число.
– волновое число.
Связь разности фаз 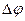 колебаний с расстоянием
колебаний с расстоянием 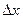 между точками среды, отсчитанным в направлении распространения колебаний:
между точками среды, отсчитанным в направлении распространения колебаний:
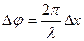
где 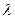 - длина волны.
- длина волны.
Импульс материальной точки массой m, движущейся со скоростью 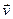 ,
,
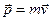
Второй закон Ньютона:
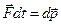
где 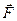 - результирующая сила, действующая на материальную точку.
- результирующая сила, действующая на материальную точку.
ЗАДАЧИ.
1. Точка движется по окружности R=1.2 м. Уравнение движения точки 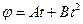 , где А=0.5 рад/с; В=0.2 рад/с2. Определить тангенциальное, нормальное и полное ускорение точки в момент времени t=4 с.
, где А=0.5 рад/с; В=0.2 рад/с2. Определить тангенциальное, нормальное и полное ускорение точки в момент времени t=4 с.
2. Определить скорость и полное ускорение точки в момент времени t=2 с, если она движется по окружности R=1 м согласно уравнению 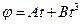 , где А=8 рад/с; В=-1рад/с3.
, где А=8 рад/с; В=-1рад/с3.
3. По прямой движутся две материальные точки согласно уравнениям: 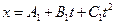 и
и 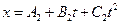 , где А1=10 м; В1=1 м/с; С1= -2 м/с2; А2=3 м; В2=2 м/с; С2= 0.2 м/с2. В какой момент времени скорости точек будут одинаковыми? Найти ускорения этих точек в момент времени t=3с.
, где А1=10 м; В1=1 м/с; С1= -2 м/с2; А2=3 м; В2=2 м/с; С2= 0.2 м/с2. В какой момент времени скорости точек будут одинаковыми? Найти ускорения этих точек в момент времени t=3с.
4. Определить полное ускорение в момент времени t=3с точки, находящейся на ободе колеса радиусом 0.5 м, движущейся согласно уравнения 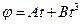 , где А=2 с–1, В=0.2 с–3.
, где А=2 с–1, В=0.2 с–3.
5. Диск радиусом 0.5 м вращается согласно уравнению 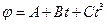 , где А=3, В= -1 с–1, С=0.1 с–3. Определить тангенциальное, нормальное и полное ускорения точек на окружности диска в момент времени t=10 c.
, где А=3, В= -1 с–1, С=0.1 с–3. Определить тангенциальное, нормальное и полное ускорения точек на окружности диска в момент времени t=10 c.
6. С высоты 2 м на стальную плиту свободно падает шарик массой 200 г и подпрыгивает на высоту 0.5 м.Определить импульс, полученный шариком при ударе.
7. При горизонтальном полете со скоростью 250 м/с снаряд массой 8 кг разорвался на две части. Большая часть снаряда массой 6 кг получила скорость 400 м/с в направлении движения снаряда. Определить величину и направление скорости меньшей части снаряда.
8. Платформа с песком общей массой 2 т стоит на рельсах. В песок попадает снаряд массой 8 кг и застревает в нем. Определить с какой скоростью начнет двигаться платформа, если скорость снаряда 450 м/с, а ее направление – сверху вниз под углом 450 к горизонту.
9. Определить импульс, полученный стенкой при ударе о нее шарика массой 300 г со скоростью 8 м/с под углом 600 к поверхности стенки. Удар считать упругим.
10. На полу стоит тележка в виде длинной доски. На одном конце тележки стоит человек массой 60 кг. Масса тележки – 20 кг. С какой скоростью будет двигаться тележка, если человек будет двигаться по ней со скоростью (относительно тележки) 1 м/с. Трением тележки о пол пренебрегаем.
11. Определить к.п.д. удара тела массой 0.5 т, падающего на сваю массой 120 кг. Полезной считать энергию, затраченную на вбивание сваи.
12. Вагон массой 35 т движется на стенку со скоростью 0.2 м/с. При полном торможении вагона буферные пружины сжимаются на 12 см.Определить максимальную силу сжатия пружин и продолжительность торможения.
13. Лодка длиной 3 м и массой 120 кг стоит на воде. На носу и корме находятся два рыбака массой 60 и 90 кг. На сколько сместится лодка, если рыбаки поменяются местами?
14. На сколько переместится относительно берега лодка длиной 3 м и массой 200 кг, если стоящий на корме человек массой 80 кг переместится на нос лодки?
15. С наклонной плоскости высотой 3 м соскальзывает без трения тело массой 0.5 кг. Определить изменение импульса тела.
16. На обод маховика диаметром 60 см намотан шнур, к концу которого привязан груз массой 2 кг. Определить момент инерции маховика, если он, вращаясь равноускоренно под действием груза, за 3 секунды приобрел скорость 9 рад/сек.
17. Стержень вращается вокруг оси, проходящей через его середину согласно уравнению 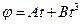 , где А=8 м/с; В= -1 м/с3.Определить вращающий момент, действующий на маховик через 2 сек. после начала вращения, если момент инерции стержня равен 4.8×10-2 кг×м2.
, где А=8 м/с; В= -1 м/с3.Определить вращающий момент, действующий на маховик через 2 сек. после начала вращения, если момент инерции стержня равен 4.8×10-2 кг×м2.
18. По горизонтальной поверхности катится диск со скоростью 8 м/с. Определить коэффициент трения, если диск предоставленный самому себе, остановился, пройдя 18 м.
19. Определить момент силы, приложенной к диску, вращающемуся с частотой 12 с–1, если диск остановился через 8 сек. Диск обладает массой 6 кг и диаметром 30 см.
20. Диск массой 0.4 кг вращается под действием силы натяжения нити, к концам которой привязаны грузы массой 0.3 и 0.7 кг. Определить силы натяжения нити по обе стороны диска.
21. На краю платформы в виде диска, вращающегося по инерции вокруг вертикальной оси с частотой 8 мин–1, стоит человек массой 70 кг. Когда человек перешел в центр платформы, она стала вращаться с частотой 10 мин–1. Определить массу платформы. Момент инерции человека рассчитать как для материальной точки.
22. Определить напряженность гравитационного поля Земли на высоте 1000 км. Считать известными радиус Земли и ускорение свободного падения на ее поверхности.
23. Из бесконечности на поверхность Земли падает метеорит массой 30 кг. Определить работу сил гравитации. Считать известными радиус Земли и ускорение свободного падения на ее поверхности.
24. С поверхности Земли вертикально вверх пущена ракета со скоростью 5 км/с. На какую высоту она поднимется?
25. Спутник движется вокруг Земли на высоте 520 км. Определить период обращения спутника. Считать известными радиус Земли и ускорение свободного падения на ее поверхности.
26. Определить угловую скорость обращения спутника Земли на высоте 1000 км, а также его линейную скорость. Считать известными радиус Земли и ускорение свободного падения на ее поверхности.
27. На краю скамьи Жуковского диаметром 0.8 м и массой 6 кг стоит человек массой 60 кг. С какой угловой скоростью начнет вращаться скамья, если человек поймает мяч массой 0.5 кг, летящий горизонтально со скоростью 5 м/с на расстоянии 0.4 м от оси вращения?
28. Платформа в виде диска диаметром 3 м и массой 180 кг может вращаться вокруг вертикальной оси. С какой угловой скоростью будет вращаться платформа, если человек массой 70 кг пойдет по ее краю со скоростью 1.8 м/с относительно платформы?
29. Платформа в виде диска массой 280 кг может вращаться вокруг вертикальной оси. На какой угол повернется платформа, если человек массой 80 кг пойдет по краю платформы и сделает полный оборот относительно платформы? Момент инерции человека рассчитать как для материальной точки.
30. Шарик массой 60 г на нити длиной 1.2 м вращается с частотой 2 с–1 вокруг вертикальной оси. На какой угол отклонится от вертикальной оси нить с шариком?
31. Определить возвращающую силу, действующую на тело массой 20 г в момент времени 0.2 с. Тело совершает гармонические колебания согласно уравнению 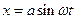 , где А=15 см и ω=4π с–1.
, где А=15 см и ω=4π с–1.
32. Определить период колебаний стержня длиной 30 см вокруг горизонтальной оси, проходящей через конец стержня.
33. Определить частоту колебаний диска радиусом 20 см вокруг горизонтальной оси, проходящей через середину радиуса диска.
34. Определить период гармонических колебаний диска вокруг горизонтальной оси проходящей через образующую диска.
35. Найти максимальную кинетическую энергию материальной точки массой 2 г, совершающей гармонические колебания с амплитудой 4 см и частотой 5 Гц.
35. Какую разность фаз будут иметь колебания, находящиеся от источника на расстоянии соответственно 10 и 16 см. Период колебаний равен 0.04 сек и скорость распространения колебаний – 300 м/с.
37. Найти разность фаз колебаний в двух точках, отстоящих друг от друга на расстоянии 2 м. Длина волны равна 1 м.
38. Смещение от положения равновесия точки, находящейся на расстоянии 4 см от источника в момент времени Т/6 равна половине амплитуды. Найти длину бегущей волны.
39. Две точки находятся на прямой, вдоль которой распространяется волна со скоростью 10 м/с. Период колебаний равен 0.2 сек., расстояние между точками равно 1 м. Найти разность фаз колебаний в этих точках.
40. Определить скорость распространения упругой волны, если разность фаз колебаний в двух точках, отстоящих друг от друга на 15 см, равна π/2. Частота колебаний равна 25 Гц.
41. Модуль ускорения свободного падения вблизи поверхности астероида равен 0,05 м/с2. Чему будет равен модуль ускорения свободного падения вблизи поверхности другого астероида, объём которого в 8 раз больше? Оба астероида однородные, сферические и состоят из железа. Ответ выразите в м/с2.
42. Два спортсмена разной массы на одинаковых автомобилях, движущихся со скоростью V=20 м/c и U= 25 м/c стали тормозить, заблокировав колеса. Каково отношение тормозных путей их автомобилей при одинаковом коэффициенте трения колес о землю?
43. Санки массой 5 кг скользят по горизонтальной дороге. Сила трения скольжения их полозьев о дорогу 6 Н. Каков коэффициент трения скольжения саночных полозьев о дорогу? Ускорения свободного падения считать равным 10 м/с2.
44. Два искусственных спутника Земли массой m=100 kg и M=300kg обращаются по круговым орбитам одинакового радиуса. Чему равно отношение скоростей этих спутников ?
45. Модуль ускорения свободного падения вблизи поверхности астероида равен 0,2 м/с2. Чему будет равен модуль ускорения свободного падения вблизи поверхности другого астероида, объём которого в 8 раз меньше? Оба астероида однородные, сферические и состоят из железа. Ответ выразите в м/с2.
46. Механическая энергия системы изменилась от величины 5 Дж до величины –3 (минус 3) Дж. Это означает, что на данную механическую систему действовали внешние силы. Какова работа этих сил?
47. Легковой автомобиль и грузовик движутся со скоростями V=20 m/c и U= 25 m/c соответственно. Масса грузовика M=3000kg. Какова масса легкового автомобиля, если импульс грузовика больше импульса легкового автомобиля на 15000 кг·м/с?
48. Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние 5 м, расстояние тела от поверхности Земли при этом увеличивается на 3 м. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила трения? Ускорение свободного падения равно 10 м/с2 коэффициент трения 0.3.
49. В инерциальной системе отсчёта тело массой 2 кг движется по прямой в одном направлении под действием постоянной силы, равной 3 Н. На сколько увеличится импульс тела за 5 с движения?
50. Какую мощность развивает двигатель подъемного механизма крана, если он равномерно поднимает плиту массой 600 кг на высоту 4 м за 3 с? (Ответ дайте в кВт.) Ускорение свободного падения принять равным 10 м/с2.
51. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 10 Н*с Каков модуль силы?
52. Тело свободно падает без начальной скорости. Изменение модуля импульса этого тела за промежуток времени 2 с равно 10 кг·м/с. Чему равна масса тела? Сопротивлением воздуха можно пренебречь.
53. Шарик массой 200 г падает с высоты 20 м с начальной скоростью, равной нулю. Какова его кинетическая энергия в момент перед ударом о землю, если потеря энергии за счёт сопротивления воздуха составила 4 Дж? (Ответ дайте в джоулях.) Ускорение свободного падения принять равным 10 м/с2.
54. На расстоянии 400 м от наблюдателя рабочие вбивают сваи с помощью копра. Каково время между видимым ударом молота о сваю и звуком удара, услышанным наблюдателем? Скорость звука в воздухе 330 м/с .
55. Для экспериментального определения скорости звука ученик встал на расстоянии 30 м от стены и хлопнул в ладоши. В момент хлопка включился электронный секундомер, который выключился отражённым звуком. Время, отмеченное секундомером, равно 0,18 с. Какова скорость звука, определённая учеником?
56. Какова частота колебаний звуковых волн в среде, если скорость звука в среде 1000м/с а длина волны 10 см?
57. Звуковой сигнал, отразившись от препятствия, вернулся обратно к источнику через 5 с после его испускания. Каково расстояние от источника до препятствия, если скорость звука в воздухе 340 м/с?
58. Скорость звука в воде 1,5 км/с. Чему равна длина звуковой волны, распространяющейся в воде, при частоте звука 3 кГц?
59. Гидроакустик, находящийся на корабле, переговаривается по рации с матросом, находящимся на лодке. Во время разговора матрос наносит удар гаечным ключом по корпусу своей лодки. Звук от этого удара гидроакустик сначала слышит через рацию, а через 10 секунд — через свою гидроакустическую аппаратуру. Считая, что второй звук распространяется в воде со скоростью 1500 м/с, найдите расстояние между кораблём и лодкой. Ответ приведите в километрах.
60. Гидроакустик, находящийся на корабле, переговаривается по рации с матросом, находящимся на лодке. Расстояние между кораблем и лодкой составляет 7,5 км. Во время разговора матрос наносит удар гаечным ключом по корпусу своей лодки. Звук от этого удара гидроакустик сначала слышит через рацию, а затем — через свою гидроакустическую аппаратуру. Считая, что второй звук распространяется в воде со скоростью 1500 м/с, найдите время между ударами, которые слышит гидроакустик.
Основные формулы.
Количество вещества однородного газа (в молях):
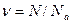 ;
; 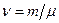
где N - число молекул газа; 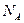 - постоянная Авогадро; m - масса газа;
- постоянная Авогадро; m - масса газа; 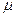 - молярная масса газа.
- молярная масса газа.
Если система представляет смесь нескольких газов, то количество вещества системы
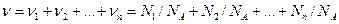 ,
,
или
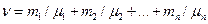 ,
,
где 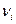 , N
, N 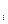 , m
, m 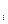 ,
, 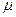
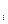 - соответственно количество вещества, число молекул, масса, молярная масса i-й компоненты смеси.
- соответственно количество вещества, число молекул, масса, молярная масса i-й компоненты смеси.
Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа):
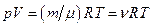 ,
,
где m - масса газа, 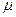 - молярная масса газа; R - универсальная газовая постоянная;
- молярная масса газа; R - универсальная газовая постоянная; 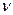 - количество вещества; T - термодинамическая температура.
- количество вещества; T - термодинамическая температура.
Опытные газовые законы, являющиеся частными случаями уравнения Менделеева-Клапейрона для изопроцессов:
- закон Бойля-Мариотта (изотермический процесс Т=const, m=const):
рV=const,
- закон Гей-Люcсака (изобарный процесс p=const, m=const):
V/T=const,
- закон Шарля (изохорный процесс V=const, m=const):
P/T=const,
- объединенный газовый закон (m=const):
PV/T=const
Закон Дальтона, определяющий давление смеси газов:
P= 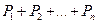
где 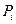 - парциальные давления компонентов смеси; n – число компонентов смеси.
- парциальные давления компонентов смеси; n – число компонентов смеси.
Парциальным давлением называется давление газа, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.
Молярная масса смеси газов:
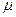 =(
=( 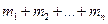 )/(
)/( 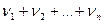 )
)
где 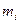 - масса i-го компонента смеси;
- масса i-го компонента смеси; 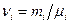 – количество вещества i-го компонента смеси; n - число компонентов смеси.
– количество вещества i-го компонента смеси; n - число компонентов смеси.
Массовая доля 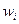 -го компонента смеси газа ( в долях единицы или процентах):
-го компонента смеси газа ( в долях единицы или процентах):
w 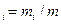
где m – масса смеси.
Концентрация молекул:
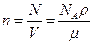
где N - число молекул, содержащихся в данной системе; 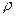 - плотность вещества, V - объём системы.
- плотность вещества, V - объём системы.
Основное уравнение кинетической теории газов:
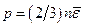
где 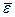 - средняя кинетическая энергия поступательного движения молекулы.
- средняя кинетическая энергия поступательного движения молекулы.
Средняя кинетическая энергия поступательного движения молекулы:
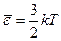
где k - постоянная Больцмана.
Средняя полная кинетическая энергия молекулы:
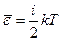
где i – число степеней свободы молекулы.
Зависимость давления газа от концентрации молекул и температуры:
р= nkT
Скорости молекул:
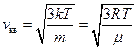 (средняя квадратичная);
(средняя квадратичная);
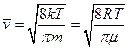 (средняя арифметическая);
(средняя арифметическая);
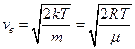 (наиболее вероятная),
(наиболее вероятная),
где m - масса одной молекулы.
Молярные теплоемкости газа при постоянном объеме ( 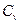 ) и при постоянном давлении (
) и при постоянном давлении ( 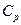 ):
):
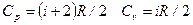
Связь между удельной c и молярной С теплоёмкостями:
с=С/ 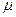
Уравнение Майера:
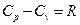
Внутренняя энергия идеального газа:
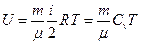
Первое начало термодинамики:
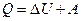
где 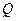 - теплота, сообщенная системе (газу);
- теплота, сообщенная системе (газу); 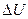 - изменение внутренней энергии системы; A - работа, совершенная системой против внешних сил.
- изменение внутренней энергии системы; A - работа, совершенная системой против внешних сил.
Работа расширения газа:
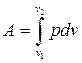 ( в общем случае);
( в общем случае);
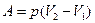 ( при изобарном процессе);
( при изобарном процессе);
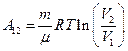 (при изотермическом процессе);
(при изотермическом процессе);

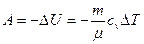 (при адиабатном процессе),
(при адиабатном процессе),
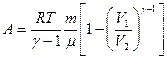
где 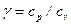 – показатель адиабаты.
– показатель адиабаты.
Уравнения Пуассона, связывающие параметры идеального газа при адиабатном процессе:
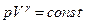
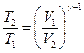
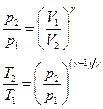
Термический к.п.д. цикла;
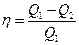
где 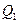 - теплота, полученная рабочим телом от теплоотдатчика,
- теплота, полученная рабочим телом от теплоотдатчика, 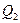 - теплота, переданная рабочим телом теплоприёмнику.
- теплота, переданная рабочим телом теплоприёмнику.
Термический к.п.д. цикла Карно:
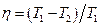
где 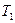 и
и 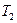 - термические температуры теплоотдатчика и теплоприёмника.
- термические температуры теплоотдатчика и теплоприёмника.
Коэффициент поверхностного натяжения:
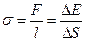
где F - сила поверхностного натяжения; действующая на контур l, ограничивающий поверхность жидкости; 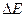 - изменение поверхностной энергии пленки жидкости, связанное с изменением площади
- изменение поверхностной энергии пленки жидкости, связанное с изменением площади 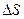 поверхности этой пленки.
поверхности этой пленки.
Формула Лапласа, выражающая давление p, создаваемое сферической поверхностью жидкости:
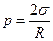
где R - радиус сферической поверхности.
Высота подъема жидкости в капиллярной трубке:
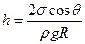
где 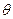 - краевой угол (
- краевой угол ( 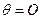 -при полном смачивании стенок трубки жидкостью;
-при полном смачивании стенок трубки жидкостью; 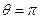 при полном несмачивании); R - радиус канала трубки; ρ - плотность жидкости; g - ускорение свободного падения.
при полном несмачивании); R - радиус канала трубки; ρ - плотность жидкости; g - ускорение свободного падения.
Высота подъёма жидкости между двумя близкими и параллельными друг другу плоскостями:
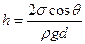
где 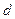 - расстояние между плоскостями.
- расстояние между плоскостями.
Средняя длина свободного пробега молекулы
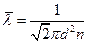
Распределение молекул в потенциальном поле сил (распределение Больцмана)
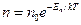
Барометрическая формула
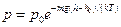
Уравнение диффузии (закон Фика)
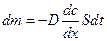
Сила внутреннего трения в жидкости и газе 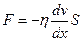
Уравнение теплопроводности 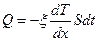
Коэффициент диффузии 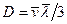
Коэффициент внутреннего трения (динамическая вязкость)
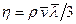
Коэффициент теплопроводности 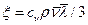
Изменение энтропии 
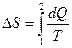
Задачи.
1. Определить количество молей вещества и количество молекул в 0.5 кг водорода.
2. Сколько атомов содержится в ртути: массой 1г; в 0.2 молях.
3. Определить массу одной молекулы углекислого газа.
4. Определить концентрацию молекул кислорода в сосуде емкостью 2 литра. Количество кислорода равно 0.2 моля.
5. В баллоне емкостью 3 литра содержится 10 г углекислого газа. Определить концентрацию молекул.
6. В цилиндр длиной 1.6 м, заполненным воздухом при атмосферном давлении, начали медленно вдвигать поршень площадью 200 см2 . Определить силу, действующую на поршень, если его остановили в 10 см от дна цилиндра.
7. В баллоне находится газ при температуре 400 К. До какой температуры его надо нагреть, чтобы давление возросло в 1.5 раза?
8. Баллон емкостью 20 л заполнен азотом при температуре 400 К. Когда часть газа израсходовали, давление понизилось на 200 кПа. Определить массу израсходованного газа. Процесс считать изотермическим.
9. В баллоне емкостью 15 л находится аргон под давлением 600 кПа и при температуре 300 К. Определить массу израсходованного газа, если давление понизилось до 400 кПа, а температура установилась в 260 К.
10. Два сосуда одинакового объема содержат кислород. В одном сосуде давление 2 МПа и температура 800 К, в другом – 2.5 МПа и 200 К. Сосуды соединили трубкой и охладили газ до 200 К. Определить установившееся в сосудах давление.
11. Определить внутреннюю энергию водорода, а также среднюю кинетическую энергию молекулы при температуре 300 К, если количество водорода равно 0.5 молей.
12. Определить суммарную кинетическую энергию поступательного движения молекул газа в сосуде емкостью 3 л под давлением 540 МПа.
13. Количество гелия 1.5 моля при температуре 120 К. Определить суммарную кинетическую энергию всех молекул газа.
14. Водород в количестве 0.5 моля находится при температуре 300 К. Найти среднюю кинетическую энергию вращательного движения молекулы и суммарную кинетическую энергию всех молекул.
15. В азоте взвешены мелкие пылинки, которые могут двигаться как крупные молекулы. Масса пылинки равна 6×10–10 г. Газ находится при температуре 400 К. Определить средние квадратичные скорости, а также средние кинетические энергии поступательного движения молекулы и пылинки.
16. Определить молярную массу двухатомного газа и его удельные теплоемкости, если известно, что разность удельных теплоемкостей этого газа равна 260 ДЖ/(кг×К).
17. Найти удельные, а также молярные теплоемкости углекислого газа.
18. Определить показатель адиабаты идеального газа, который при температуре 350 К и давлении 0.4 МПа занимает объем 300 л и имеет теплоемкость 857 Дж/К.
19. В сосуде емкостью 6 л находится при нормальных условиях двухатомный газ. Определить теплоемкость этого газа при постоянном объеме.
20. Вычислить удельные теплоемкости газа, зная, что его молярная масса равна 4*10–3 кг/моль и отношение теплоемкостей равно 1.67.
21. Определить среднюю длину свободного пробега молекулы азота в сосуде емкостью 5 литров. Масса газа равна 0.5 г.
22. Водород находится под давлением 20 мкПа и имеет температуру 300 К. Определить среднюю длину свободного пробега молекул газа.
23. Какова средняя арифметическая скорость молекул кислорода, если известно, что при нормальном давлении средняя длинна свободного пробега молекул равна 100 нм?
24. При каком давлении средняя длинна свободного пробега молекул азота равна 1 м, если температура газа равна 100С?
25. Средняя длинна свободного пробега молекулы водорода при некоторых условиях равна 2 мм. Найти плотность водорода при этих условиях.
26. Определить количество теплоты, которое надо сообщить кислороду объемом 50 л при изохорном нагревании, чтобы давление газа повысилось на 0.5 МПа.
27. При изотермическом расширении азота при температуре 280 К объем его увеличился в 2 раза. Определить:1) совершенную газом работу; 2) изменение внутренней энергии газа; 3) количество теплоты, полученной газом. Масса газа равна 0.2 кг.
28. При адиабатическом сжатии давление воздуха было увеличено с 50 кПа до 0.5 МПа. Затем при неизменном объеме температура воздуха была понижена до первоначальной. Определить давление газа в конце процесса.
29. Кислород массой 200 г занимает объем 100 л и находится под давлением в 200 кПа. При Нагревании газ изобарно расширился до объема 300 л, а затем его давление изохорно возросло до 500 кПа. Найти изменение внутренней энергии газа, совершенную им работу и полученную теплоту. Построить график процесса.
30. Азот массой 100 г изобарно нагрет от температуры 200 К до температуры 400 К. Определить работу газа, полученную теплоту и изменение внутренней энергии.
31. Идеальный газ совершает цикл Карно при температурах теплоприемника 290 К и теплоотдатчика 400 К. Во сколько раз увеличится к.п.д. цикла, если температура нагревателя возрастет до 600 К?
32. Идеальный газ совершает цикл Карно. Температура нагревателя в 4 раза больше температуры холодильника. Какую долю количества теплоты, полученного за один цикл от нагревателя, газ отдаст приемнику?
33. Газ, совершающий цикл Карно, отдал холодильнику теплоту в 14 кДж. Определить температуру нагревателя, если при температуре холодильника 280 К работа за цикл равна 6 кДж.
34. Определить работу изотермического сжатия газа, совершающего цикл Карно, к.п.д. которого равно 0.4, если работа изотермического расширения равна 8 Дж.
35. Идеальная тепловая машина работает при температурах нагревателя 500 К и холодильника 250 К. Определить к.п.д. машины, а также работу при изотермическом расширении, если работа при изотермическом сжатии равна 70 Дж.
36. Найти массу воды, вошедшей в стеклянную трубку диаметром 0.8 мм, опущенную в воду на малую глубину. Считать смачивание полным.
37. Какую работу надо совершить при выдувании мыльного пузыря, чтобы увеличить его объем от 8 см3 до 16 см3. Процесс считать изотермическим.
38. Какая энергия выделится при слиянии двух капель ртути диаметром 0.8 мм и 1.2 мм в одну каплю?
39. Определить давление внутри воздушного пузырька диаметром 4 мм, находящегося в воде у самой ее поверхности. Считать атмосферное давление нормальным.
40. Пространство между двумя стеклянными пластинами с поверхностью 100 см2 каждая, расположенными на расстоянии 20 мкм друг от друга, заполнено водой. Определить силу притяжения между пластинами. Мениск в зазоре считать вогнутым с диаметром, равным расстоянию между пластинами.
41. Во сколько раз изменится давление разреженного газа, если при его нагревании и сжатии абсолютная температура газа и концентрация молекул увеличатся в 2 раза?
42. В результате охлаждения одноатомного идеального газа его давление уменьшилось в 4 раза, а концентрация молекул газа не изменилась. Чему равно отношение конечной средней кинетической энергии теплового движения молекул газа к начальной?
43. При неизменном давлении одноатомного идеального газа среднеквадратичная скорость движения его атомов увеличилась в 2 раза. Чему равно отношение конечной плотности газа к начальной?
44. В закрытом сосуде объёмом 20 литров находится 5 моль кислорода. Температура газа равна 127 °С. Чему равно давление газа? Ответ выразите в кПа.
45. В закрытом сосуде объёмом 10 литров находится 5 моль азота. Температура газа равна 26 °С. Чему равно давление газа? Ответ выразите в килопаскалях и округлите до целого числа.
46. Идеальный одноатомный газ в количестве 0,05 моль подвергся адиабатическому сжатию. При этом его температура повысилась с +23 °C до +63 °C. Какая работа была совершена над газом? Ответ выразите в джоулях и округлите до целого числа.
47. Тепловая машина с КПД 40% за цикл работы отдаёт холодильнику количество теплоты, равное 60 Дж. Какое количество теплоты машина получает за цикл от нагревателя? (Ответ дайте в джоулях.)
48. Идеальный газ получил количество теплоты 300 Дж и при этом внутренняя энергия газа увеличилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)
49. В процессе эксперимента внутренняя энергия газа уменьшилась на 40 кДж, и он совершил работу 35 кДж. Какое количество теплоты (в кДж) газ отдал окружающей среде?
50. Тепловая машина с КПД 40% за цикл работы получает от нагревателя количество теплоты, равное 300 Дж. Какую работу машина совершает за цикл? Ответ приведите в джоулях.
51. Температура холодильника тепловой машины 400 К, температура нагревателя на 200 К больше, чем у холодильника. Каков максимально возможный КПД машины? (Ответ дайте в процентах, округлив до целых.)
52. В таблице приведена зависимость КПД идеальной тепловой машины от температуры ее нагревателя при неизменной температуре холодильника. Чему равна температура холодильника этой тепловой машины? (Ответ дайте в кельвинах.)
52. Некоторое число молей одноатомного идеального газа изохорически нагревается из состояния p1 = 105 Па и t1 = 27 °С до давления p2 = 2p1. Чему равна совершённая газом работа?
53. Алюминиевому и железному цилиндрам сообщили одинаковое количество теплоты, что привело к увеличению температуры цилиндров, причём увеличение температуры алюминиевого цилиндра оказалось в 2 раза больше, чем железного. Определите отношение масс этих цилиндров. Удельная теплоёмкость железа равна 460 Дж/(кг·К), алюминия — 900 Дж/(кг·К).
55. Относительная влажность воздуха в цилиндре под поршнем равна 70 %. Воздух изотермически сжали, уменьшив его объём в два раза. Какова стала относительная влажность воздуха? (Ответ дайте в процентах.)
56. Алюминиевому и железному цилиндрам одинаковой массы сообщили одинаковое количество теплоты. Определите примерное отношение изменения температур этих цилиндров . Удельная теплоёмкость железа равна 460 Дж/(кг·К), алюминия — 900 Дж/(кг·К).
57. Температура медного образца массой 100 г повысилась с 20 °С до 60 °С. Какое количество теплоты получил образец? Удельную теплоёмкость меди считать равной 1620Дж/кг*К
58. Какое количество теплоты необходимо для плавления 2,5 т стали, взятой при температуре плавления? Теплопотерями пренебречь. Ответ выразите в МДж.
59. В сосуде объёмом 1,5 л при температуре +50 °C находится смесь воздуха с водяными парами. Давление в сосуде равно 99,4 кПа, относительная влажность воздуха 50 %. Давление насыщенного водяного пара при данной температуре равно 12,5 кПа. Какое количество воздуха находится в сосуде?
60. Относительная влажность воздуха в закрытом сосуде 25 %. Какой будет относительная влажность, если объём сосуда при неизменной температуре уменьшить в 3 раза? (Ответ дать в %)
Основные формулы.
Закон Кулона:
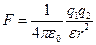
где F - сила взаимодействия точечных зарядов 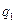 и
и 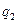 ;
; 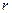 - расстояние между зарядами;
- расстояние между зарядами; 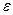 - диэлектрическая проницаемость;
- диэлектрическая проницаемость; 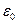 -электрическая постоянная.
-электрическая постоянная.
Напряженность электрического поля и потенциал:
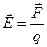
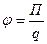
где П - потенциальная энергия точечного положительного заряда q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).
Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда:
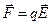
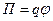
Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей):
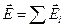
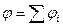
где 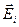 ,
, 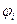 - напряженность и потенциал в данной точке поля, создаваемого i -м зарядом.
- напряженность и потенциал в данной точке поля, создаваемого i -м зарядом.
Напряженность и потенциал поля, создаваемого точечным зарядом:
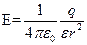
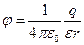
где 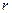 - расстояние от заряда q до точки, в которой определяются напряженность и потенциал.
- расстояние от заряда q до точки, в которой определяются напряженность и потенциал.
Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом R на расстоянии 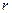 от центра сферы:
от центра сферы:
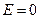
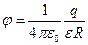 , (при r < R)
, (при r < R)
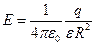
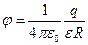 , (при r = R)
, (при r = R)
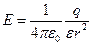
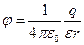 (при r>R)
(при r>R)
где q – заряд сферы.
Линейная плотность заряда:
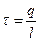
Поверхностная плотность заряда:
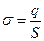
Напряженность и потенциал поля, создаваемого распределенными зарядами. Если заряд равномерно распределен вдоль линии с линейной плотностью 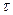 , то на линии выделяется малый участок длиной
, то на линии выделяется малый участок длиной 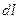 с зарядом
с зарядом 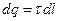 . Такой заряд можно рассматривать как точечный и применять формулы:
. Такой заряд можно рассматривать как точечный и применять формулы:
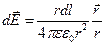
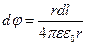
где r - радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.
Используя принцип суперпозиции электрических полей, находим интегрированием напряженность 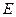 и потенциал φ поля, создаваемого распределенным зарядом:
и потенциал φ поля, создаваемого распределенным зарядом:
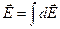
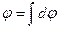
Интегрирование ведется вдоль всей длины l заряженной линии.
Напряженность поля, создаваемого бесконечной прямой равномерно заряженной нитью или бесконечно длинным цилиндром:
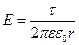
где r - расстояние от нити или оси цилиндра до точки, напряженность поля в которой вычисляется.
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью:
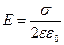
Связь потенциала с напряженностью:
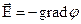 , или
, или 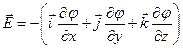 (в общем случае),
(в общем случае),
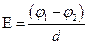 , (в случае однородного поля);
, (в случае однородного поля);
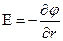 (в случае поля, обладающего центральной или осевой симметрией).
(в случае поля, обладающего центральной или осевой симметрией).
Электрический момент диполя:
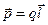 ,
,
где q - заряд; 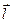 - плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
- плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
Работа сил поля по перемещению заряда q из точки поля с потенциалом 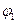 в точку с потенциалом
в точку с потенциалом 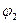 :
:
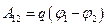
Электроемкость:
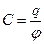 или
или 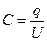 ,
,
где 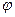 - потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U
- потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U  - разность потенциалов пластин конденсатора.
- разность потенциалов пластин конденсатора.
Электроемкость уединенной проводящей сферы радиусом R:
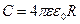
Электроемкость плоского конденсатора:
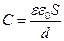
где S - площадь пластины конденсатора; d - расстояние между пластинами.
Электроемкость батареи конденсаторов:
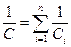 (при последовательном соединении)
(при последовательном соединении)
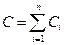 (при параллельном соединении),
(при параллельном соединении),
где n -число конденсаторов в батарее.
Энергия заряженного конденсатора:
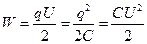
Сила тока: 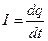 ,
,
где 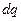 - заряд, прошедший через поперечное сечение проводника за время
- заряд, прошедший через поперечное сечение проводника за время 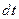 .
.
Плотность тока:
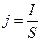 ,
,
где S - площадь поперечного сечения проводника.
Связь плотности тока со средней скоростью 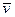 направленного движения заряженных частиц:
направленного движения заряженных частиц:
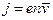 ,
,
где е - заряд частицы; n - концентрация заряженных частиц.
Закон Ома:
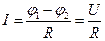 (для участка цепи, не содержащего э.д.с.)
(для участка цепи, не содержащего э.д.с.)
где 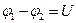 - разность потенциалов (напряжение) на концах участка цепи; R - сопротивление участка;
- разность потенциалов (напряжение) на концах участка цепи; R - сопротивление участка;
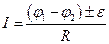 (для участка цепи, содержащего э.д.с),
(для участка цепи, содержащего э.д.с),
где 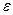 - э.д.с. источника тока; R - полное сопротивление участка цепи.
- э.д.с. источника тока; R - полное сопротивление участка цепи.
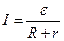 (для замкнутой цепи),
(для замкнутой цепи),
где R - внешнее сопротивление цепи; r - внутреннее сопротивление цепи.
Законы Кирхгофа:
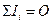 , (первый закон);
, (первый закон);
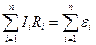 , (второй закон),
, (второй закон),
где 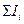 - алгебраическая сумма токов, сходящихся в узле;
- алгебраическая сумма токов, сходящихся в узле; 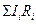 - алгебраическая сумма падений напряжения в контуре;
- алгебраическая сумма падений напряжения в контуре; 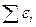 - алгебраическая сумма э.д.с., действующих в контуре.
- алгебраическая сумма э.д.с., действующих в контуре.
Сопротивление R и проводимость G проводника:
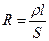 ;
; 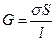
где 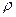 - удельное сопротивление;
- удельное сопротивление; 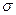 - удельная проводимость;
- удельная проводимость;  l - длина проводника;
l - длина проводника; 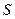 - площадь поперечного сечения проводника.
- площадь поперечного сечения проводника.
Сопротивление системы проводников:
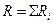 (при последовательном соединении);
(при последовательном соединении);
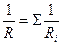 (при параллельном соединении),
(при параллельном соединении),
где 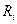 - сопротивление i -гo проводника.
- сопротивление i -гo проводника.
Работа силы тока:
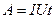 ;
; 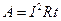 ;
; 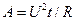 .
.
Мощность тoкa:
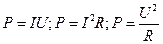
Закон Джоуля-Ленца:
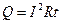
Закон Ома в дифференциальной форме:
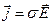
где 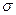 - удельная проводимость,
- удельная проводимость, 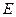 - напряженность электрического поля,
- напряженность электрического поля,  - плотность тока.
- плотность тока.
Связь удельной проводимости с подвижностью 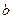 заряженных частиц (ионов):
заряженных частиц (ионов):
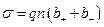 ,
,
где q -заряд иона; n -концентрация ионов; 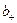 и
и 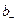 - подвижности положительных и отрицательных ионов.
- подвижности положительных и отрицательных ионов.
Задачи.
1. Точечные заряды 20 мкКл и (- 10) мкКл находятся на расстоянии 5см друг от друга. Определить напряженность поля в точке, удаленной на 3 см от первого и 4 см от второго заряда. Определить также силу F, действующую в этой точке на точечный заряд 1 мкКл.
2. Два положительных точечных заряда q и 9q закреплены на расстоянии 100 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения заряда возможны только вдоль прямой, проходящей через закрепленные заряды.
3. На расстоянии d= 20 см находятся два точечных заряда - 50 нКл и 100 нКл. Определить силу, действующую на заряд –10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d.
4. По тонкой нити, изогнутой по дуге окружности радиусом 10 см, равномерно распределен заряд 20 нКл. Определить напряженность поля, создаваемого этим зарядом в точке, совпадающей с центром кривизны дуги, если длина нити равна четверти длины окружности.
5. Определить напряженность поля, создаваемого зарядом, равномерно распределенным по тонкому прямому стержню с линейной плотностью заряда 200 нКл/м в точке, лежащей на продолжении оси стержня на расстоянии 20 см от ближайшего конца. Длина стержня 40 см.
6. По тонкому кольцу радиусом 10 см равномерно распределен заряд 20 нКл. Какова напряженность поля в точке, находящейся на оси кольца на расстоянии 20 см от центра кольца?
7. Две одинаковые круглые пластины площадью 400 см 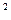 каждая расположены параллельно друг другу. Заряд одной пластины 400 нКл, другой - 200 нКл. Определить силу взаимного притяжения пластин, если расстояние между ними: а)3 мм; б)10 м.
каждая расположены параллельно друг другу. Заряд одной пластины 400 нКл, другой - 200 нКл. Определить силу взаимного притяжения пластин, если расстояние между ними: а)3 мм; б)10 м.
8. Четыре одинаковых капли ртути, заряженных до потенциала 10 В, сливаются в одну. Каков потенциал образовавшейся капли?
9. Электрическое поле образовано бесконечно длинной заряженной нитью, линейная плотность заряда которой 20 пКл/м. Определить разность потенциалов двух точек поля, отстоящих от нити на расстоянии 8 см и 12 см.
10. Электрон с энергией 400 эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом 10 см. Определить минимальное расстояние а, на которое приблизится электрон к поверхности сферы, если заряд ее 10 нКл.
11. Пылинка массой 5 мкг, несущая на себе 10 электронов, прошла в вакууме ускоряющую разность потенциалов 1 мВ. Какова кинетическая энергия пылинки? Какую скорость приобрела пылинка?
12. Расстояние между пластинами плоского конденсатора 2 мм, разность потенциалов 600 В. Заряд каждой пластинки 40 нКл. Определить энергию поля конденсатора и силу взаимного притяжения пластин.
13. Два конденсатора емкостью 5 мкф и 8 мкф соединены последовательно и присоединены к батарее с э.д.с. 80 В. Определить заряды конденсаторов и разности потенциалов между их обкладками.
14. Два металлических шарика радиусами 5 и 10 см имеют заряды 40нКл и –20 нКл соответственно. Найти энергию, которая выделится при разряде, если шары соединить проводником.
15. Как надо соединить конденсаторы емкостью 2 пФ, 4 пФ, 6 пФ, чтобы получить систему с емкостью 3 пФ?
16. Между обкладками воздушного конденсатора параллельно им влетает электрон со скоростью 1000 км/с. Длина обкладок равна 5 см, напряженность поля равна 30 В. На какой угол отклонится электрон на выходе из конденсатора?
17. Между обкладками воздушного конденсатора параллельно им по середине влетает протон со скоростью 100 м/с. Длина обкладок равна 10 см, а расстояние между ними равно 1 см. При каком минимальном напряжении протон не вылетит из конденсатора?
18. Между пластин конденсатора висит капелька масла с зарядом 3*10–8 Кл и массой 6 мкг. Определить объемную плотность энергии поля конденсатора.
19. Два элемента с э.д.с. 1.6 и 2 В и внутренним сопротивлением 0.3 и 0.9 Ом соответственно соединены последовательно и замкнуты на внешнее сопротивление 2 Ом. Найти силу тока в цепи.
20. Батарея из двух параллельно соединенных источников с э.д.с. 2 и 1.8 В и внутренним сопротивлением 0.05 Ом каждый замкнуты на сопротивление 2 Ом. Найти токи в цепи.
21. Э.д.с. батареи 80 В, внутреннее сопротивление 5 Ом. Внешняя цепь потребляет мощность 100 Вт. Определить силу тока в цепи, напряжение , под которым находится внешняя цепь и ее сопротивление .
22. Определить число электронов, проходящих за время 1с через поперечное сечение площадью 1 мм 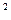 железной проволоки длиной 20 м при напряжении на ее концах 16 В.
железной проволоки длиной 20 м при напряжении на ее концах 16 В.
23. При внешнем сопротивлении 8 Ом сила тока в цепи 0,8 А, при сопротивлении 15 Ом сила тока 0,5А. Определить силу тока короткого замыкания источника э.д.с.
24. Э.д.с. батареи 12 В. При силе тока 4 А к.п.д. батареи 0,6. Определить внутреннее сопротивление батареи.
25. Сила тока в проводнике сопротивлением 10 Ом за время 50 с равномерно нарастает от 5 А до 10 А. Определить количество теплоты Q, выделившееся за это время в проводнике.
26. Резистор сопротивлением 6 Ом подключен к двум параллельно соединенным источникам тока с э.д.с. 2,2 В и 2,4 В и внутренними сопротивлениями 0,8 Ом и 0,2 Ом. Определить силу тока в этом резисторе и напряжение на зажимах второго источника тока.
27. Найти величину тока в обмотке троллейбусного двигателя, развивающего силу тяги 6000 Н при напряжении в сети 600 В и движущегося со скоростью 54 км/ч. К.п.д. двигателя 80 %.
28. Электрочайник имеет две спирали. При включении одной из них вода в чайнике закипает через 15 минут, при включении другой – через 30 минут. Через сколько минут закипит чай ник, если включить обе спирали последовательно?
29. Электрочайник имеет две спирали. При включении одной из них вода в чайнике закипает через 15 минут, при включении другой – через 30 минут. Через сколько минут закипит чай ник, если включить обе спирали параллельно?
30. Найти, при каком значении сопротивления внешней цепи мощность, отдаваемая источником тока, максимальна и каково при этом значение тока в цепи.
31. В электронагревателе с неизменным сопротивлением спирали, через который течёт постоянный ток, за время t выделяется количество теплоты Q. Если силу тока и время t увеличить вдвое, то во сколько раз увеличится количество теплоты, выделившееся в нагревателе?
32. Студент проводил эксперименты, соединяя друг с другом различными способами батарейку и пронумерованные лампочки. Сопротивление батарейки и соединительных проводов было пренебрежимо мало. Измерительные приборы, которые использовал школьник, можно считать идеальными. Сопротивление всех лампочек не зависит от напряжения, к которому они подключены. Ход своих экспериментов и полученные результаты школьник заносил в лабораторный журнал. Вот что написано в этом журнале:
Опыт А). Подсоединил к батарейке лампочку № 1. Сила тока через батарейку 2 А, напряжение на лампочке 8 В.
Опыт Б). Подключил лампочку № 2 последовательно с лампочкой № 1. Сила тока через лампочку №1 равна 1 А, напряжение на лампочке № 2 составляет 4 В.
Опыт В). Подсоединил параллельно с лампочкой № 2 лампочку № 3. Сила тока через лампочку № 1 примерно 1,14 А, напряжение на лампочке № 2 примерно 3,44 В.
Исходя из записей в журнале определите сопротивление лампочки № 3.
34. К источнику тока с ЭДС 2 В подключен конденсатор емкостью 1 мкФ. Какое тепло выделится в цепи в процессе зарядки конденсатора? Эффектами излучения пренебречь.
35. В лаборатории есть два проводника круглого сечения. Удельное сопротивление первого проводника в 2 раза больше удельного сопротивления второго проводника. Длина первого проводника в 2 раза больше длины второго. При подключении этих проводников к одинаковым источникам постоянного напряжения за одинаковые интервалы времени во втором проводнике выделяется количество теплоты в 4 раза меньшее, чем в первом. Чему равно отношение радиуса первого проводника к радиусу второго проводника?
36. На цоколе электрической лампы накаливания написано: «220 В, 60 Вт». Две такие лампы соединяют параллельно и подключают к напряжению 127 В. Какая мощность будет выделяться в двух этих лампах при таком способе подключения? При решении задачи считайте, что сопротивление лампы не зависит от приложенного к ней напряжения.
37. Между двумя точечными заряженными телами сила электрического взаимодействия равна 20 мН. Если заряд одного тела увеличить в 4 раза, а заряд другого тела уменьшить в 5 раз и расстояние между телами уменьшить в 2 раза, то какова будет сила взаимодействия между телами?
38. Какова разность потенциалов между точками поля, если при перемещении заряда 12 мкКл из одной точки в другую электростатическое поле совершает работу 0,36 мДж?
39. Между двумя точечными заряженными телами сила электрического взаимодействия равна 12 мН. Если заряд одного тела увеличить в 3 раза, а заряд другого тела уменьшить в 4 раза и расстояние между телами уменьшить в 2 раза, то какова будет сила взаимодействия между телами?
40. Между двумя точечными заряженными телами сила электрического взаимодействия равна 24 мН. Если заряд одного тела увеличить в 2 раза, а заряд другого тела уменьшить в 3 раза и расстояние между телами увеличить в 2 раза, то какова будет сила взаимодействия между телами?
41. Между двумя точечными заряженными телами сила электрического взаимодействия равна 20 мН. Если заряд одного тела увеличить в 4 раза, а заряд другого тела уменьшить в 5 раз и расстояние между телами уменьшить в 2 раза, то какова будет сила взаимодействия между телами?
42. Между двумя точечными заряженными телами сила электрического взаимодействия равна 12 мН. Если заряд одного тела увеличить в 2 раза, а заряд другого тела уменьшить в 3 раза и расстояние между телами уменьшить в 2 раза, то какова будет сила взаимодействия между телами?
43. Модуль напряженности однородного электрического поля равен 100 В/м. Каков модуль разности потенциалов между двумя точками, расположенными на одной силовой линии поля на расстоянии 5 см?
44. Два точечных заряда — отрицательный, равный по модулю 3 мкКл, и положительный, равный по модулю 4 мкКл, расположены на расстоянии 1 м друг от друга. На расстоянии 1 метр от каждого из этих зарядов помещают положительный заряд Q, модуль которого равен 2 мкКл. Определите модуль силы, действующей на заряд Q со стороны двух других зарядов?
45. Два точечных отрицательных заряда, равных по модулю 3 мкКл и 4 мкКл, расположены на расстоянии 1 м друг от друга. На расстоянии 1 м от каждого из зарядов помещают положительный заряд Q, модуль которого равен 2 мкКл. Определите модуль силы, действующей на заряд Q со стороны двух других зарядов. Ответ выразите в Н и округлите до десятых долей.
46. С какой силой взаимодействуют в вакууме два маленьких заряженных шарика, находящихся на расстоянии 4 м друг от друга? Заряд каждого шарика 8 · 10−8 Кл. Ответ выразите в мкН.
47. Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает с поверхности пластинки электрон, который попадает в электрическое поле с напряженностью 125 В/м. Найти расстояние, которое он пролетит прежде, чем разгонится до скорости, равной 1% от скорости света.
48. Идеальный амперметр и три резистора сопротивлением и включены последовательно в электрическую цепь, содержащую источник с равной 5 В, и внутренним сопротивлением Каковы показания амперметра?
49. Через проводник постоянного сечения течёт постоянный ток силой 1 нА. Сколько электронов в среднем проходит через поперечное сечение этого проводника за 0,72 мкс?
50. Модуль напряжённости электрического поля в плоском воздушном конденсаторе ёмкостью 50 мкФ равен 200 В/м. Расстояние между пластинами конденсатора 2 мм. Чему равен заряд этого конденсатора?
51. Заряд плоского воздушного конденсатора ёмкостью 25 мкФ равен 50 мкКл. Расстояние между пластинами конденсатора равно 2 см. Чему равен модуль напряжённости электрического поля между пластинами?
52. Через поперечное сечение проводников за 8 с прошло 1020 электронов. Какова сила тока в проводнике?
53. Напряжённость поля между пластинами плоского воздушного конденсатора равна по модулю 25 В/м, расстояние между пластинами 15 мм, ёмкость конденсатора 12 мкФ. Определите заряд этого конденсатора.
54. Напряжённость поля между пластинами плоского воздушного конденсатора равна по модулю 50 В/м, расстояние между пластинами 12 мм, заряд конденсатора 15 мкКл. Определите ёмкость этого конденсатора.
55. Чему равно время прохождения тока силой 5 А по проводнику, если при напряжении на его концах 120 В в проводнике выделяется количество теплоты, равное 540 кДж? (Ответ дайте в секундах.)
56. В электронагревателе с неизменным сопротивлением спирали, через который течёт постоянный ток, за время t выделяется количество теплоты Q. Если силу тока и время t увеличить вдвое, то во сколько раз увеличится количество теплоты, выделившееся в нагревателе?
57. Резистор 1 с электрическим сопротивлением 3 Ом и резистор 2 с электрическим сопротивлением 6 Ом включены последовательно в цепь постоянного тока. Чему равно отношение количества теплоты, выделяющегося на резисторе 1, к количеству теплоты, выделяющемуся на резисторе 2 за одинаковое время?
58. К источнику тока с ЭДС 2 В подключён конденсатор ёмкостью 1 мкФ. Какую работу совершил источник при зарядке конденсатора? (Ответ дайте в мкДж.)
59. К источнику тока с ЭДС 2 В подключен конденсатор емкостью 1 мкФ. Какое тепло выделится в цепи в процессе зарядки конденсатора? (Ответ дайте в мкДж.) Эффектами излучения пренебречь.
60. К идеальному источнику тока с ЭДС 3 В подключили конденсатор ёмкостью 1 мкФ один раз через резистор R=10кOм а второй раз — через резистор r=20кОм. Во сколько раз во втором случае тепло, выделившееся на резисторе, больше по сравнению с первым? Излучением пренебречь.
Электромагнетизм.
Основные формулы.
Связь магнитной индукции 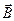 и напряженностью
и напряженностью 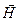 магнитного поля:
магнитного поля:
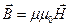
где 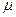 – магнитная проницаемость среды;
– магнитная проницаемость среды; 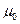 – магнитная постоянная. В вакууме
– магнитная постоянная. В вакууме 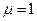 , и тогда магнитная индукция в вакууме
, и тогда магнитная индукция в вакууме
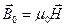
Закон Био-Савара-Лапласа:
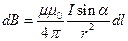 ,
,
где 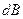 магнитная индукция поля, создаваемого элементом проводника длиной
магнитная индукция поля, создаваемого элементом проводника длиной 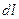 с током
с током 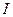 ,
, 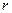 - радиус–вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция;
- радиус–вектор, направленный от элемента проводника к точке, в которой определяется магнитная индукция; 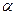 - угол между радиус–вектором и направлением тока в элементе проводника.
- угол между радиус–вектором и направлением тока в элементе проводника.
Магнитная индукция в центре кругового тока:
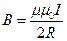
где 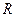 - радиус витка.
- радиус витка.
Магнитная индукция на оси кругового тока:
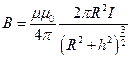 ,
,
где 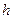 - расстояние от центра витка до точки, в которой определяется магнитная индукция.
- расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля прямого тока:
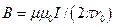 ,
,
где 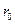 - расстояние от оси проводника до точки, в которой определяется магнитная индукция.
- расстояние от оси проводника до точки, в которой определяется магнитная индукция.
Магнитная индукция поля, создаваемого отрезком провода с током:
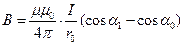
Магнитная индукция поля соленоида:
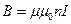 ,
,
где 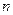 - отношение числа витков соленоида к его длине.
- отношение числа витков соленоида к его длине.
Сила, действующая на проводник с током в магнитном поле
(закон Ампера):
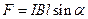 .
.
где I = сила тока, 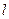 - длина проводника,
- длина проводника, 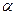 - угол между направлением тока в проводнике и вектором магнитной индукции В. Это выражение справедливо для однородного магнитного поля и прямого отрезка проводника. Если поле неоднородно и проводник не является прямым, то закон Ампера можно применять к каждому элементу проводника в отдельности:
- угол между направлением тока в проводнике и вектором магнитной индукции В. Это выражение справедливо для однородного магнитного поля и прямого отрезка проводника. Если поле неоднородно и проводник не является прямым, то закон Ампера можно применять к каждому элементу проводника в отдельности:
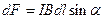
Работа по перемещению проводника с током в магнитном поле:
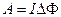
Э.д.с. индукции:
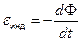
Индуктивность катушки: 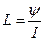
где 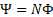 - потокосцепление.
- потокосцепление.
Э.д.с. самоиндукции:
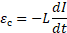
Индуктивность соленоида: 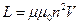
где 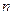 - отношение числа витков соленоида к его длине; V - объем соленоида.
- отношение числа витков соленоида к его длине; V - объем соленоида.
Мгновенное значение силы тока в цепи, обладающей сопротивлением 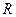 и индуктивностью
и индуктивностью 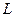 :
:
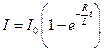 (при замыкании цепи),
(при замыкании цепи),
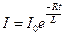 (при размыкании цепи),
(при размыкании цепи),
где 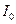 - сила тока в цепи при
- сила тока в цепи при 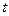 = 0.
= 0.
Энергия магнитного поля:
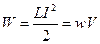
где V - объем соленоида.
Объемная плотность энергии магнитного поля:
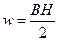 , или
, или 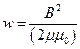 , или
, или 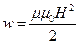
где В - магнитная индукция; Н - напряженность магнитного поля.
Магнитный момент плоского контура с током:
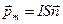
где 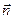 - единичный вектор нормали к плоскости контура;
- единичный вектор нормали к плоскости контура; 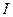 - сила тока, протекающего по контуру;
- сила тока, протекающего по контуру; 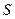 - площадь контура.
- площадь контура.
Механический (вращательный) момент, действующий на контур с током, помещенный в однородное магнитное поле:
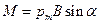 ,
,
где 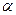 - угол между векторами
- угол между векторами 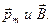
Потенциальная энергия контура с током в магнитном поле:
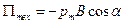
Отношение магнитного момента 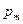 к механическому
к механическому 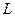 (моменту импульса) заряженной частицы, движущейся по круговой орбите:
(моменту импульса) заряженной частицы, движущейся по круговой орбите:
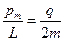
где q - заряд частицы; 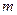 - масса частицы.
- масса частицы.
Сила Лоренца:
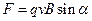
где 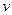 - скорость заряженной частицы,
- скорость заряженной частицы, 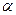 - угол между векторами
- угол между векторами 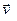 и
и 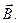
Магнитный поток:
в случае однородного магнитного поля и плоской поверхности
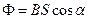 или
или 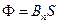 ,
,
где 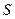 - площадь контура;
- площадь контура; 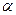 - угол между нормалью к плоскости контура и вектором магнитной индукции:
- угол между нормалью к плоскости контура и вектором магнитной индукции:
в случае неоднородного поля и произвольной поверхности:
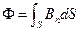
(интегрирование ведётся по всей поверхности).
Потокосцепление:
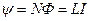
Эта формула верна для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.
Задачи.
1. По двум длинным параллельным проводам, расстояние между которыми 5 см, текут одинаковые токи 10 А. Определить индукцию и напряженность магнитного поля в точке, удаленной от каждого провода на расстояние 5 см, если токи текут: а) в одинаковом б) в противоположных направлениях.
2. По проводнику, согнутому в виде прямоугольника со сторонами 8 см и 12см, течет ток силой 50 А. Определить напряженность и индукцию магнитного поля в точке пересечения диагоналей прямоугольника.
3. По двум параллельным проводам длиной 3 м каждый текут одинаковые токи силой 500 А. Расстояние между проводниками 10 см. Определить силу взаимодействия проводников.
4. Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны проводу. По раме и проводу текут одинаковые токи силой 200 А. Определить силу, действующую на рамку, если ближайшая к проводу сторона рамки находится от него на расстоянии, равном ее длине.
5. Прямой провод длиной 40 см, по которому течет ток силой 100 А, движется в однородном магнитном поле с индукцией 0,5 Тл. Какую работу совершат силы, действующие на провод со стороны поля, переместив его на расстояние 40 см, если направление перемещения перпендикулярно линиям индукции и проводу?
6. Напряженность магнитного поля в центре круглого витка равна 500 А/м. Магнитный момент витка 6 А м 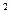 . Вычислить силу тока в витке и радиус витка.
. Вычислить силу тока в витке и радиус витка.
7. Виток радиусом 20 см, по которому течет ток силой 50 А, свободно установился в однородном магнитном поле напряженностью 10 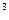 А/м. Виток повернули относительно диаметра на угол 30
А/м. Виток повернули относительно диаметра на угол 30 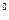 . Определить совершенную работу А.
. Определить совершенную работу А.
8. Диск радиусом 5 см несет равномерно распределенный по поверхности заряд 0,1 мкКл. Диск равномерно вращается относительно оси, проходящей через его центр и перпендикулярной плоскости диска. Частота вращения 50 с 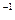 . Определить: 1) магнитный момент кругового тока, создаваемого диском; 2) отношение магнитного момента к моменту импульса, если масса диска 100 г.
. Определить: 1) магнитный момент кругового тока, создаваемого диском; 2) отношение магнитного момента к моменту импульса, если масса диска 100 г.
9. По тонкому стержню длиной 40 см равномерно распределен заряд 50 нКл. Стержень приведен во вращение с постоянной угловой скоростью 20 рад/с относительно оси, перпендикулярной стержню и проходящей через его середину. Определить: 1) магнитный момент, обусловленный вращением заряженного стержня; 2) отношение магнитного момента к моменту импульса, если стержень имеет массу 10 г.
10. Электрон в атоме водорода движется вокруг ядра по круговой орбите некоторого радиуса. Найти отношение магнитного момента эквивалентного кругового тока к моменту импульса орбитального движения электрона. Заряд электрона и его массу считать известными. Указать на чертеже направление векторов .
11. Электрон движется в однородном магнитном поле перпендикулярно линиям индукции. Определить силу, действующую на электрон со стороны поля, если индукция поля 0,2 Тл, а радиус кривизны траектории 0,2 см.
12. Электрон движется по окружности в однородном магнитном поле с напряженностью 5∙10 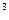 А/м. Определить частоту обращения n электрона.
А/м. Определить частоту обращения n электрона.
13. Протон влетел в однородное магнитное поле под углом 60 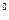 к направлению линий поля и движется по винтовой линии, радиус которой 2,5 см. Индукция магнитного поля 0,05 Тл. Найти кинетическую энергию протона.
к направлению линий поля и движется по винтовой линии, радиус которой 2,5 см. Индукция магнитного поля 0,05 Тл. Найти кинетическую энергию протона.
14. В однородном магнитном поле с индукцией 2 Тл движется a–частица. Траектория ее движения представляет собой винтовую линию с радиусом 1 см и шагом 6 см. Определить кинетическую энергию протона.
15. Магнитный поток сквозь сечение соленоида равен 50 мкВб. Длина соленоида равна 50 см. Найти магнитный момент соленоида, если его витки плотно прилегают друг к другу.
16. Виток, в котором поддерживается постоянная сила тока 60 А, свободно установился в однородном магнитном поле (В = 20 мТл). Диаметр витка 10 см. Какую работу нужно совершить для того, чтобы повернуть виток относительно оси, совпадающей с диаметром, на угол p/3?
17. Рамка, содержащая 1000 витков площадью 100 см 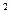 , равномерно вращается с частотой 10 с
, равномерно вращается с частотой 10 с 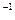 в магнитном поле напряженностью 10
в магнитном поле напряженностью 10 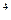 А/ м. Ось вращения лежит в плоскости рамки и перпендикулярна линиям напряженности. Определить максимальную э.д.с. индукции, возникающую в рамке.
А/ м. Ось вращения лежит в плоскости рамки и перпендикулярна линиям напряженности. Определить максимальную э.д.с. индукции, возникающую в рамке.
18. Проволочный виток диаметром 5 см и сопротивлением 0, 02 Ом находится в однородном магнитном поле (В = 0,3 Тл). Плоскость витка составляет угол 45  с линиями индукции. Какой заряд потечет по витку при выключении магнитного поля?
с линиями индукции. Какой заряд потечет по витку при выключении магнитного поля?
19. Чему равен поток магнитной индукции в железном тороиде квадратного сечения со стороной 5 см, содержащем обмотку из 400 витков, по которому течет ток в 2 А? Диаметр тороида равен 25 см. Относительная магнитная проницаемость железа равна 400.
20. По замкнутой цепи с сопротивлением R = 20 Ом течет ток. Через время t = 8 мс после размыкания цепи сила тока в ней уменьшилась в 20 раз. Определить индуктивность L цепи.
21. Определить разность потенциалов возникающую на концах вертикальной автомобильной антенны длиной 1.2 м при движении автомобиля с востока на запад в магнитном поле Земли со скоростью 72 км/ч. Горизонтальная составляющая магнитного поля Земли равна 16 А/м.
22. Определить индуктивность катушки, если при изменении в ней тока от 0 до5 А за 2 сек возникает э.д.с. самоиндукции 1 В.
23. Найти индуктивность соленоида, полученного при намотке провода длиной 10 м на цилиндрический железный стержень длиной 10 см. Относительная магнитная проницаемость железа равна 400.
24. Определить энергию магнитного поля соленоида, содержащего 500 витков, намотанных на картонный каркас радиусом 2 см и длиной 0.5 м, если по нему течет ток 5 А.
25. Заряженный конденсатор емкостью 0.5 мкФ подключен к катушке с индуктивностью 5 мГн. Через сколько времени энергия электрического поля конденсатора будет равна энергии магнитного поля катушки? Сопротивлением катушки пренебречь.
26. В колебательном контуре, состоящем из конденсатора и катушки с индуктивностью 5 мГн, происходят электромагнитные колебания с максимальным значением тока 10 мА. Определить емкость конденсатора, если максимальная разность потенциалов на его обкладках достигает 50 В. Сопротивлением катушки пренебречь.
27. На какую длину волны настроен радиоприемник, если его приемный контур обладает индуктивностью 1.5мГн и емкостью 450 пФ.
28. Определить скорость распространения электромагнитных колебаний в стекле с диэлектрической проницаемостью равной 7 и магнитной проницаемостью равной 1.
29. Телевизор настроен на частоту 600 МГц. Индуктивность приемного контура равна 2 мГн. Определить электроемкость контура.
30. Электромагнитная волна частоты 3 МГц переходит из вакуума в диэлектрик с относительной диэлектрической проницаемостью 4. Найти приращение ее длины волны.
32. Прямолинейный проводник длиной L с током I помещен в однородное магнитное поле так, что направление вектора магнитной индукции B перпендикулярно проводнику. Если силу тока уменьшить в 2 раза, а индукцию магнитного поля увеличить в 4 раза, то как изменится действующая на проводник сила Ампера.
33. Линии индукции однородного магнитного поля пронизывают рамку площадью 1 кв.м под углом 30° к её поверхности, создавая магнитный поток, равный 0,2 Вб. Чему равен модуль вектора индукции магнитного поля? (Ответ дать в теслах.)
34. Какая энергия запасена в катушке индуктивности, если известно, что при протекании через неё тока силой 0,5 А поток, пронизывающий витки её обмотки, равен 6 Вб? Ответ выразите в Дж.
35. В опыте по наблюдению электромагнитной индукции квадратная рамка из одного витка тонкого провода находится в однородном магнитном поле, перпендикулярном плоскости рамки. Индукция магнитного поля равномерно возрастает от 0 до максимального значения Вмакс за время Т. При этом в рамке возбуждается ЭДС индукции, равная 6 мВ. Какая ЭДС индукции возникнет в рамке, если Т уменьшить в 3 раза, а Вмакс уменьшить в 2 раза? Ответ выразите в мВ.
36. По проволочной катушке протекает постоянный электрический ток силой 2 А. При этом поток вектора магнитной индукции через контур, ограниченный витками катушки, равен 4 мВб. Чему будет равен поток вектора магнитной индукции через этот контур (в мВб), если по катушке будет протекать постоянный электрический ток силой 0,5 А?
37. В состав колебательного контура входят конденсатор ёмкостью 2 мкФ, катушка индуктивности L и ключ. Соединение осуществляется при помощи проводов с пренебрежимо малым сопротивлением. Вначале ключ разомкнут, а конденсатор заряжен до напряжения 8 В. Затем ключ замыкают. Чему будет равна запасённая в конденсаторе энергия через 1/6 часть периода колебаний, возникших в контуре? Ответ выразите в мкДж.
38. В колебательном контуре, состоящем из конденсатора и катушки индуктивности, происходят свободные электромагнитные колебания. Как изменится частота колебаний, если площадь пластин конденсатора уменьшить в два раза?
39. В обмотке соленоида, сопротивление которой R = 1,0 Ом
индуктивность L = 20 мГн, сила тока 7 = 5,0 А. Чему равна энергия магнитного поля соленоида через f = 1,0 мс после отключения источника?
40. Сколько ампер-витков потребуется для того, чтобы внутри соленоида малого диаметра и длиной 30 см объемная плотность энергии магнитного поля была равна 1,75 Дж/м3?
41. Сколько ампер-витков потребуется для создания магнитного потока Ф=0,42 мВб в соленоиде с железным сердечником длиной 120 см и площадью поперечного сечения 3 см2?
42. Из проволоки длиной 20 см сделаны квадратный и круговой контуры. Найти вращающие моменты сил, действующие на каждый контур, помещенный в однородное магнитное поле с индукцией 0,1 Тл. По контурам течет ток 1=2 А. Плоскость каждого контура составляет угол а=45° с направлением поля.
43. В однородном магнитном поле с /индукцией ’ 5=0,5 Тл движется равномерно проводник длиной /=10 см.
44. По проводнику течет ток 2 А. Скорость движения проводника 20 см/с и направлена перпендикулярно к направлению магнитного поля. Найти работу перемещения проводника за время 10 с и мощность , затраченную на это перемещение.
45. Электрон, ускоренный разностью потенциалов 300 В, движется параллельно прямолинейному длинному проводу на расстоянии 4 мм от него. Какая сила F действует на электрон, если по проводнику пустить ток 5 А?
46. Найти кинетическую энергию в эВ протона, движущегося по дуге окружности радиусом 60 см в магнитном поле с индукцией 1 Тл.
47. Протон и α-частица влетают в однородное магнитное поле, направление которого перпендикулярно к направлению их движения. Во сколько раз период обращения протона в магнитном поле больше периода обращения α-частицы?
48. Найти отношение q/m для заряженной частицы, если она, влетая со скоростью 108 м/с в однородное магнитное поле напряженностью 200 кА/м и движется по дуге окружности радиусом 8,3 см. Направление скорости движения частицы перпендикулярно к направлению магнитного поля.
49. Скорость самолета с реактивным двигателем 950 км/ч. Найти э. д. с. индукции , возникающую на концах крыльев такого самолета, если вертикальная составляющая напряженности земного магнитного поля равна 39,8 А/м и размах крыльев самолета 12,5 м.
50. Катушка длиной 20 см имеет 400 витков. Площадь поперечного сечения катушки 9 см.кв. Найти индуктивность катушки. Какова будет индуктивность катушки, если внутрь катушки введен железный сердечник? Магнитная проницаемость материала сердечника μ=400.
51. Соленоид длиной 50 см и площадью поперечного сечения 2 см2 имеет индуктивность 0,2 мкГн. При каком токе объемная плотность энергии магнитного поля внутри соленоида w = l мДж/м3?
52. Круговой контур радиусом г=2 см помещен в однородное магнитное поле, индукция которого В=0,2 Тл. Плоскость контура перпендикулярна к направлению магнитного поля. Сопротивление контура R = l Ом. Какое количество электричества q пройдет через катушку при повороте ее на угол а=90°?
53. Круговой контур радиусом 2 см помещен в однородное магнитное поле, индукция которого 0,2 Тл. Плоскость контура перпендикулярна к направлению магнитного поля. Сопротивление контура l Ом. Какое количество электричества пройдет через катушку при повороте ее на угол в 90°?
54. Катушка имеет индуктивность 0,144 Гн и сопротивление 10 Ом. Через какое время t после включения в катушке потечет ток, равный половине установившегося?
55. В колебательном контуре, состоящем из конденсатора и катушки индуктивностью 5,0 мГн, происходят электромагнитные колебания, при которых максимальная сила тока 10 мА. Определить емкость конденсатора, если максимальная разность потенциалов на его обкладках достигает 50 В, а активным сопротивлением катушки можно пренебречь.
56. Колебательный контур состоит из конденсатора емкостью 2,0 мкФ и катушки индуктивностью 0,10 Гн и сопротивлением 10 Ом. Определить логарифмический декремент затухания колебаний.
57. Определить активное сопротивление колебательного контура, индуктивность которого L = 1,0 Гн, если через 0,10 с амплитудное значение разности потенциалов на обкладках конденсатора уменьшилось в 4 раза.
58. Определить частоту собственных колебаний колебательного контура, содержащего конденсатор емкостью С = 0,50 мкФ, если максимальная разность потенциалов на его обкладках достигает U m = 100 В, а максимальная сила тока в катушке равна 50 мА. Активным сопротивлением катушки пренебречь.
59. Уравнение изменения со временем тока в колебательном контуре имеет вид I=0,02 sin 400 wt А. Индуктивность контура L=1 Гн. Найти период колебаний, емкость контура, максимальную энергию магнитного поля и максимальную энергию электрического поля.
60. Уравнение изменения со временем разности потенциалов на обкладках конденсатора в колебательном контуре имеет вид U=50cos 104π В. Емкость конденсатора 0,1 мкФ. Найти период колебаний, индуктивность контура, закон изменения со временем t тока в цепи и длину волны , соответствующую этому контуру.
Оптика.
Основные формулы.
Скорость света в среде:
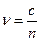
- где с скорость света в вакууме; 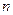 - показатель преломления среды.
- показатель преломления среды.
Оптическая длина пути световой волны:
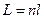
где 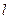 - геометрическая длина пути световой волны в среде с показателем преломления
- геометрическая длина пути световой волны в среде с показателем преломления 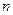 .
.
Оптическая разность хода двух световых волн:
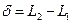
Зависимость разности фаз от оптической разности хода световых волн:
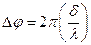
где 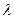 –длина световой волны.
–длина световой волны.
Условие максимального усиления света при интерференции:
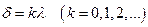
Условие максимального ослабления света:
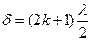 ,
, 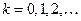
Оптическая разность хода световых волн, возникающих при отражении монохроматического света от тонкой пленки:
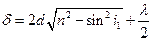
или
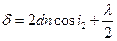 ,
,
где 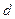 - толщина пленки ;
- толщина пленки ;  - показатель преломления пленки;
- показатель преломления пленки; 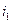 - угол падения ;
- угол падения ; 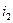 - угол преломления света в пленке.
- угол преломления света в пленке.
Радиус светлых колец Ньютона в отраженном свете:
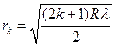 ,
, 
где 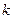 - номер кольца;
- номер кольца; 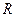 - радиус кривизны линзы.
- радиус кривизны линзы.
Радиус темных колец Ньютона в отраженном свете:
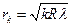
Условие максимума при дифракции на щели:
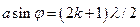

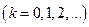
где 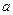 - ширина щели;
- ширина щели; 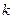 - порядковый номер максимума.
- порядковый номер максимума.
Условие максимума при дифракции на дифракционной решетке:
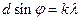
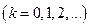
где 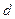 - период дифракционной решетки.
- период дифракционной решетки.
Разрешающая способность дифракционной решетки:
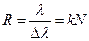
где 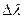 - наименьшая разность длин волн двух соседних спектральных линий
- наименьшая разность длин волн двух соседних спектральных линий 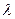 и
и 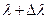 , при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки;
, при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки; 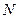 - полное число щелей решетки.
- полное число щелей решетки.
Формула Вульфа-Брэгга:
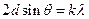 ,
,
где 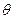 - угол скольжения / угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл и атомной плоскостью в кристалле; /
- угол скольжения / угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл и атомной плоскостью в кристалле; / 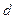 - расстояние между атомными плоскостями кристалла.
- расстояние между атомными плоскостями кристалла.
Закон Брюстера :
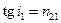
где 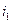 - угол падения, при котором отразившийся от диэлектрика луч полностью поляризован;
- угол падения, при котором отразившийся от диэлектрика луч полностью поляризован; 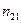 - относительный показатель преломления второй среда относительно первой.
- относительный показатель преломления второй среда относительно первой.
Закон Малюса:
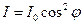
где  - интенсивность плоско поляризованного света, падающего на анализатор;
- интенсивность плоско поляризованного света, падающего на анализатор;  - интенсивность света после анализатора;
- интенсивность света после анализатора;  - угол между плоскостью колебаний светового вектора, падающего на анализатор, и плоскостью пропускания анализатора.
- угол между плоскостью колебаний светового вектора, падающего на анализатор, и плоскостью пропускания анализатора.
Угол поворота плоскости поляризации монохроматического света при прохождения через оптически активное вещество:
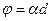 (в твердых телах),
(в твердых телах),
где 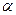 - постоянная вращения ;
- постоянная вращения ; 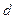 - длина пути, пройденного светом в оптически активном веществе;
- длина пути, пройденного светом в оптически активном веществе;
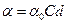 (в растворах),
(в растворах),
где 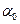 - удельное вращение; C - концентрация оптически активного вещества в растворе.
- удельное вращение; C - концентрация оптически активного вещества в растворе.
Релятивистская масса:
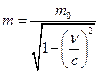
где 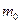 - масса покоя частицы;
- масса покоя частицы; 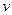 - ее скорость ; c - скорость света в вакууме.
- ее скорость ; c - скорость света в вакууме.
Взаимосвязь массы и энергии релятивистской частицы:
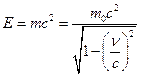
Полная энергия свободной частицы:
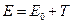
где 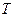 – кинетическая энергия релятивистской частицы;
– кинетическая энергия релятивистской частицы; 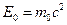 - энергия покоя частицы.
- энергия покоя частицы.
Импульс релятивистской частицы:
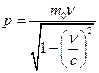
Связь между полной энергией и импульсом релятивистской частицы:
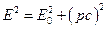
Закон Стефана – Больцмана:
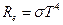 ,
,
где  - энергетическая светимость (излучательная способность) абсолютно черного тела;
- энергетическая светимость (излучательная способность) абсолютно черного тела; 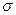 - постоянная Стефана-Больцмана ; Т - термодинамическая температура тела.
- постоянная Стефана-Больцмана ; Т - термодинамическая температура тела.
Закон смещения Вина:
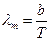
где  - длина волны, на которую приходится максимум спектральной излучательной способности;
- длина волны, на которую приходится максимум спектральной излучательной способности;
b - постоянная Вина.
Энергия фотона:
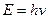 , или
, или 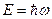
где 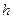 - постоянная Планка ;
- постоянная Планка ; 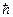 - постоянная Планка, деленная на
- постоянная Планка, деленная на 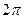 ;
; 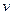 - частота колебаний;
- частота колебаний; 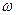 - циклическая частота.
- циклическая частота.
Релятивистская масса фотона:
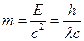
где с - скорость света в вакууме; 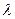 - длина волны фотона.
- длина волны фотона.
Импульс фотона:
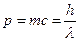
Формула Эйнштейна для фотоэффекта:
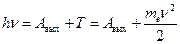
где 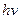 - энергия фотона, падающего на поверхность металла;
- энергия фотона, падающего на поверхность металла; 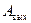 - работа выхода электрона; T -максимальная кинетическая энергия фотоэлектрона.
- работа выхода электрона; T -максимальная кинетическая энергия фотоэлектрона.
Красная граница внешнего фотоэффекта:
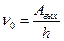 или
или 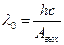
где  - минимальная частота света, при которой еще возможен фотоэффект;
- минимальная частота света, при которой еще возможен фотоэффект;  - максимальная длина волны света, при которой еще возможен фотоэффект;
- максимальная длина волны света, при которой еще возможен фотоэффект; 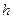 - постоянная Планка;
- постоянная Планка; 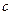 - скорость света в вакууме.
- скорость света в вакууме.
Формула Комптона:
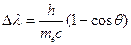
или
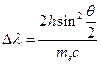
где 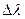 - изменение длины волны фотона, рассеянного на электроне;
- изменение длины волны фотона, рассеянного на электроне; 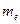 - масса покоя электрона;
- масса покоя электрона; 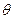 - угол рассеивания фотона.
- угол рассеивания фотона.
Давление света на поверхность:
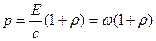
где Е – освещенность поверхности; с – скорость света: 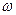 – объемная плотность энергии излучения;
– объемная плотность энергии излучения; 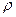 – коэффициент отражения.
– коэффициент отражения.
Задачи.
1. Тонкая пленка с показателем преломления п =1,5 освещается рассеянным светом с длиной волны 600 нм. При какой минимальной толщине пленки исчезнут интерференционные полосы?
2. На плоской прозрачной поверхности образована тонкая прозрачная пленка толщиной 0,396 мкм. Какую окраску примет пленка при освещении ее белым светом, падающим под углом 30°?Показатель преломления стекла 1,5, а материала пленки 1,4.
Определить толщину слоя масла на поверхности воды, если при наблюдении под углом 60° к нормали в спектре отраженного света видна значительно усиленная желтая линия с длиной волны к = 0,589 мкм.
3. Каково расстояние между 20-м и 21-м максимумами светлых колец Ньютона, если расстояние между 2-м и 3-м — 1 мм, а наблюдение ведется в отраженном свете?
- Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой находится жидкость. Найти показатель преломления жидкости, если радиус третьего темного кольца Ньютона при наблюдении в отраженном свете с длиной волны 0,6 мкм равен 0,82 мм. Радиус кривизны линзы равен 0.5 м.
5. На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны 500 нм. Отраженный от неё свет максимально усилен вследствие интерференции. Определить минимальную толщину пленки, если показатель преломления материала пленки равен 1.4.
6. Нa стеклянную пластинку положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом длиной волны 500 нм. Найти радиус линзы, если радиус четвертого темного кольца Ньютона в отраженном свете равен 2 мм.
7. Нa тонкую глицериновую пленку толщиной 1.5 мкм нормально к ее поверхности падает белый свет. Определить длины волн лучей видимого участка спектра (λ=0.4–0.8 мкм), которые будут ослаблены в результате интерференции.
8. Дифракционная решетка содержит 100 штрихов на 1 мм длины. Определить длину волны монохроматического света, падающего на решетку нормально, если угол между двумя максимумами 1-го порядка 8°.
9. Какой наибольший порядок спектра натрия (𝜆 = 590 нм) можно наблюдать при помощи дифракционной решетки, имеющей 500 штрихов на 1 мм, если свет падает на решетку под углом 30°?
10. Спектры 2-го и 3-го порядков в видимой области дифракционной решетки частично перекрываются. Какой длине волны в спектре 3-го порядка соответствует 𝜆 = 700 нм в спектре 2-го порядка?
11. Постоянная дифракционной решетки в 4 раза больше длины световой волны монохроматического света, нормально падающего на ее поверхность. Определить угол между двумя первыми симметричными дифракционными максимумами.
12. Расстояние между штрихами дифракционной решетки 4 мкм. Нa решетку падает нормально свет с длиной волны 0,58 мкм. Максимум какого наибольшего порядка дает эта решетка?
13. Нa поверхность дифракционной решетки нормально к ее поверхности падает монохроматический свет. Постоянная дифракционной решетки в 4,6 раза больше длины световой волны. Найти общее число дифракционных максимумов, которые теоретически возможно наблюдать в данном случае.
14. Чему равен угол полной поляризации вещества, у кото-
рого предельный угол полного внутреннего отражения 42°?
15. Луч естественного света отражается от плоского
стеклянного дна сосуда, наполненного водой. Каков должен быть угол падения луча, чтобы отраженный луч был максимально поляризован? Показатель преломления стекла 1,52, воды — 1,33.
16. Определить толщину кварцевой пластинки, для которой угол поворота плоскости поляризации света длиной волны 490 нм равен 150°. Постоянная вращения в кварце для этой длины волны 26,3°/мм.
- Концентрация раствора сахара, налитого в стеклянную
трубку, равна 0,3 г/см3. Этот раствор вращает плоскость поляризации монохроматического света на 25°. Определить концентрацию раствора в другой такой же трубке, если он вращает плоскость поляризации на 20°.
- Угол падения луча на поверхность стекла равен 600. При этом отраженный пучок света оказался максимально поляризованным. Определить угол преломления луча.
- Угол между плоскостями пропускания поляроидов равен 500 . Естественный свет, проходя через такую систему, ослабляется в 4 раза. Пренебрегая потерей света при отражении, определить коэффициент поглощения света в поляроидах.
- Пучок света, идущий в стеклянном сосуде с глицерином, отражается от дна сосуда. Пpи каком угле падения отраженный пучок света максимально поляризован ?
- Параллельный пучок света переходит из глицерина в стекло так, что пучок, отражённый от границы раздела этих сред, оказывается максимально поляризованным. Определить угол между падающим и преломленным пучками.
- Частица движется со скоростью с/3 (где с – скорость света в вакууме). Какую долю энергии покоя составляет кинетическая энергия частицы?
- Протон с кинетической энергией 3 Гэв при торможении потерял треть этой энергии. Определить во сколько раз изменился релятивистский импульс протона.
- При какой скорости (в долях от скорости света) релятивистская масса любой частицы вещества в 3 раза больше массы покоя?
- Скорость электрона равна 0.8 с (где с – скорость света в вакууме). Зная энергию покоя электрона в мегаэлектрон–вольтах, определить в тех же единицах кинетическую энергию электрона.
- Во сколько раз энергия фотона ( 𝜆 = 550 нм) больше средней кинетической энергии поступательного движения молекулы кислорода при комнатной температуре (17°С)?
- При помощи индукционного ускорителя электронов (бетатрона) можно получить фотоны у-лучей с энергией 100 МэВ. Какова длина волны этих лучей?
- Какой длиной волны должен обладать фотон, чтобы его релятивистская масса была равна массе покоя электрона.
- При какой температуре средняя кинетическая энергия теплового движения молекул одноатомного газа равна энергии фотонов рентгеновских лучей (𝜆= 0,1 нм)?
- Какова максимальная скорость электронов, вылетающих с поверхности молибдена при освещении его лучами с длиной волны 200 нм?
- Какую скорость (в долях скорости света) нужно сообщить частице, чтобы её кинетическая энергия была равна удвоенной энергии покоя?
- Земля вследствие излучения в среднем ежеминутно теряет с поверхности площадью 1 м2 энергию 5,4 кДж. При какой температуре абсолютно черное тело излучало бы такую же энергию?
- Вычислить энергию, излучаемую с поверхности Солнца площадью 1 м2 за 1 мин, приняв температуру его поверхности равной 6 000 К. Считать, что Солнце излучает как абсолютно черное тело.
- Температура абсолютно черного тела 127°С. После повышения температуры суммарная мощность излучения увеличилась в 3 раза. На сколько повысилась при этом температура?
- 19. Абсолютно чёрное тело имеет температуру 500 К. Какова будет температура тела, если в результате нагревания поток излучения увеличивается 5 раз?
- 20. Определить температуру и энергетическую светимость (излучательную способность) абсолютно чёрного тела, если максимум энергии излучения приходится на длину волны 600 нм.
- Из смотрового окошечка печи излучается поток 4 кДж/мин. Определить температуру печи, если площадь окошечка равна 8 см2.
- Поток излучения абсолютно чёрного тела равен 10 кВт, максимум энергии излучения приходится на длину волны 0,8 мкм. Определить площадь излучающей поверхности.
- Как и во сколько раз изменится поток излучения абсолютно чёрного тела, если максимум энергии излучения переместится с красной границы видимого спектра (780 нм) на фиолетовую (390 нм).
- Красная граница фотоэффекта для платины лежит около 198 нм. Если платину прокалить при высокой температуре, то красная граница фотоэффекта станет равной 220 нм. На сколько электрон-вольт прокаливание уменьшает работу выхода электронов?
- Красная граница фотоэффекта рубидия 810 нм. Какое задерживающее напряжение нужно приложить к фотоэлементу, чтобы ни одному из электронов, испускаемых рубидием под действием ультрафиолетовых лучей с длиной волны 100 нм, не удалось преодолеть задерживающее поле?
- Красная граница фотоэффекта для цинка равна 310 нм. Определить максимальную кинетическую энергию фотоэлектронов в электрон–вольтах, если на цинк падает свет с длиной волны 200 нм.
- Нa поверхность калия падает свет с длиной волны 150 нм. Определить максимальную кинетическую энергию фотоэлектронов.
- Фотон с энергией 10 эВ падает на серебряную пластику и вызывает фотоэффект. Определить импульс, полученный пластинкой, если принять, что направление движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластин.
- На фотоэлемент с катодом из лития падает свет с длиной волны 200 нм. Найти наименьшее значение задерживающей разности потенциалов, которую нужно приложить к фотоэлементу, чтобы прекратить фототок.
- На металлическую пластину направлен пучок ультрафиолетового излучения с длиной волны 0,25 мкм. Фототок прекращается при минимальной задерживающей разности потенциалов в 0,96 В. Определять работу выхода электронов из металла.
- Рентгеновское излучение с длинной волны 1нм, рассеивается электронами, которые можно считать практически свободными. Определить максимальную длину волны рентгеновского излучения в рассеянном пучке.
- Фотон с энергией Е = 0,75 МэВ рассеялся на свободном электроне под углом в 60°. Найти энергию рассеянного фотона Е, кинетическую энергию и импульс электрона отдачи. Кинетической энергией электрона до соударения пренебречь.
- Фотон жестких рентгеновских лучей (𝜆 = 24 пм) при соударении со свободным электроном передал ему 9% своей энергии. Определить длину волны рассеянного рентгеновского излучения.
- γ-лучи с длиной волны 2,7 пм испытывают комптоновское рассеяние. Во сколько раз длина волны излучения, рассеянного под углом 180° к первоначальному направлению, больше длины волны падающего излучения?
- γ-лучи с длиной волны 2,7 пм испытывают комптоновское рассеяние. Во сколько раз длина волны излучения, рассеянного под углом 180° к первоначальному направлению, больше длины волны падающего излучения?
- Какая доля энергии фотона переходится при эффекте Комптона к электрону отдачи, если рассеяние фотона происходит на угол π/2? Энергия фотона до рассеяния равна 0,51 МэВ.
- Определить максимальное изменение длины волны при комптоновском рассеянии света на свободных электронах и свободных протонах.
- Фотон с энергией в 0,51 МэВ был рассеян при эффекте Комптона на свободном электроне на угол 1800. Определить кинетическую энергию электрона отдачи.
- В результате эффекта Комптона фотон с энергией 1,02 МэВ рассеян на свободных электронах на угол 1500. Определить энергию рассеянного фотона.
- В классических опытах П. Н. Лебедева по экспериментальному определению светового давления поток лучистой энергии направляется на крылышки весьма чувствительных крутильных весов. Вычислить давление, которое испытывали зачерненные и зеркальные крылышки измерительной установки, если поток падающей световой энергии равен 1,05 кДж/(м2-с).
- Давление излучения на плоское зеркало 0,2 Па. Определить интенсивность света, падающего на поверхность зеркала с коэффициентом отражения 0,6. Считать, что световой поток нормально падает на поверхность зеркала.
- Световой поток мощностью 9 Вт нормально падает на поверхность площадью S = 10 см2, коэффициент отражения которой равен 0,8. Какое давление испытывает при этом данная поверхность?
- Электрическая лампа рассчитана на мощность N = = 45 Вт, Вычислить давление лучистой энергии на зеркальную поверхность с коэффициентом отражения, равным 1, расположенную нормально к падающим лучам на расстоянии 1 м от лампы.
- 35. Определить энергетическую освещенность зеркальной поверхности, если давление, производимое излучением равно 40 мкПа. Излучение падает нормально к поверхности.
- 36. Давление света с длиной волны 400 нм, падающего нормально на черную поверхность равно 2 нПа. Определить число фотонов, падающих за время 10 с на площадь в 1 мм2.
Основы квантовой механики.
Основные формулы.
Момент импульса электрона (постулат Бора):
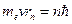
где 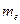 – масса электрона ; v – скорость электрона на
– масса электрона ; v – скорость электрона на 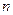 –ой орбите;
–ой орбите; 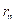 радиус
радиус 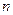 –ой стационарной орбиты;
–ой стационарной орбиты;  – постоянная Планка;
– постоянная Планка; 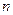 – главное квантовое число (n=1,2,…).
– главное квантовое число (n=1,2,…).
Радиус 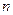 –ой стационарной орбиты:
–ой стационарной орбиты:
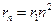
где 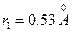 – радиус Бора.
– радиус Бора.
Энергия электрона в атоме водорода:
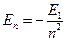
где 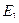 =13,6 эВ – энергия ионизации атома водорода.
=13,6 эВ – энергия ионизации атома водорода.
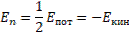
Энергия, излучаемая или поглощаемая атомом водорода:
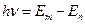
или,
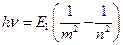
где m и n квантовые числа, соответствующие энергетическим уровням, между которыми совершаются переход электрона в атоме.
Длина волны де Бройля:
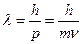
где p – импульс частицы.
Соотношение неопределённостей Гейзенберга:
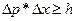 (для координаты и импульса);
(для координаты и импульса);
где  р – неопределённость импульса по оси
р – неопределённость импульса по оси 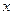 ;
;
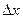 – неопределённость координаты:
– неопределённость координаты:
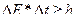 (для энергии и времени),
(для энергии и времени),
где 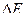 – неопределённость энергии;
– неопределённость энергии; 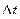 – время нахождения квантовой системы в данном энергетическом состоянии.
– время нахождения квантовой системы в данном энергетическом состоянии.
Одномерное уравнение Шредингера для стационарных состояний:
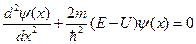
где 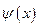 – волновая функция, описывающая состояние частицы;
– волновая функция, описывающая состояние частицы; 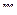 – масса частицы;
– масса частицы; 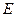 – полная энергия; U – потенциальная энергия частицы.
– полная энергия; U – потенциальная энергия частицы.
Плотность вероятности нахождения частицы в точке с координатой x:
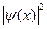 .
.
Вероятность обнаружения частицы в интервале от 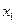 до
до 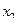 :
:
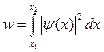
Решение уравнения Шредингера для одномерного, бесконечно глубокого, прямоугольного потенциального ящика:
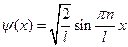
Собственные значения энергии частицы в потенциальном бесконечно глубоком «ящике»:
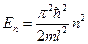
где  – квантовое число (
– квантовое число ( 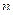 =1,2,3,…);
=1,2,3,…); 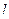 – ширина ящика (
– ширина ящика ( 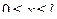 ).
).
Задачи.
1. Определить первый потенциал возбуждения и энергию ионизации атома водорода, находящегося в основном состоянии.
2. Определить энергию фотона, испускаемого атомом водорода при переходе электрона с третьей орбиты на вторую.
3. Найти наибольшую и наименьшую длины волны в ультрафиолетовой серии водорода (серия Лаймана).
- В однозарядном ионе гелия электрон перешел с третьего энергетического уровня на первый. Определить длину волны излучения, испущенного ионом гелия.
5. Электрон в атоме водорода находится на третьем энергетическом уровне. Определить кинетическую, потенциальную и полную энергию электрона. Ответ выразить в электрон–вольтах.
6. Фотон выбивает из атома водорода, находящегося в основном состоянии, электрон с кинетической энергией 10 эВ. Определить энергию фотона.
7. Во сколько раз увеличится радиус орбиты электрона
у атома водорода, находящегося в основном состоянии, при
возбуждении его фотоном энергией 12,09 эВ?
8. Какую работу нужно совершить, чтобы удалить электрон со второй орбиты атома водорода за пределы притяжения его ядром?
9. Определить длину волны де Бройля для частицы массой 1 г, движущейся со скоростью 10 м/с. Нужно ли учитывать в этом случае волновые свойства частицы?
10. Вычислить длину волны де Бройля для протона с кинетической энергией 100 эВ.
11. В телевизионной трубке проекционного типа электроны разгоняются до скорости 108 м/с. Определить длину волны катодных лучей без учета и с учетом зависимости массы от скорости.
12. Какую ускоряющую разность потенциалов должен пройти
протон, чтобы длина волны де Бройля была равна: 1 нм?
- Вычислить длину волны де Бройля протона, прошедшего ускоряющую разность потенциалов, равную: а) 1 MB ; в) 1 ГВ.
- Электрон обладает кинетической энергией 1,02 МэВ. Во сколько раз изменится длина волны де Бройля, если кинетическая энергия электрона уменьшится вдвое?
15. Кинетическая энергия электрона равна удвоенному значению его энергии покоя. Вычислить длину волны де Бройля для такого электрона.
16. Частица находится в бесконечно глубоком, одномерном прямоугольном потенциальном ящике. Найти отношение разности соседних энергетических уровней к энергии частицы в трех случаях: 1) n =2; 2) n=5; 3) n= 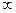 .
.
17. Используя соотношение неопределенностей, оценить наименьшие ошибки в определении импульса электрона и протона, если, координаты центра масс этих частиц могут быть установлены с неопределенностью ∆x =0.01мм
18. Время жизни возбуждённого ядра порядка 10 нс, длина волны излучения равна 0,1 нм. С какой наибольшей точностью может быть определена энергия излучения?
- Частица в бесконечно, глубоком, одномерном, потенциальном, прямоугольном, ящике находится в основном состоянии. Какова вероятность обнаружения частицы в крайней четверти ящика?
20. Используя соотношение неопределенностей, оценить ширину одномерного потенциального ящика, в котором минимальная энергия электрона 10эВ.
21. Альфа частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Используя соотношение неопределенностей, оценить ширину ящика, если известно, что минимальная энергия α – частицы равна 8 МэВ.
22. Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной 0,1 нм. Определить в эВ наименьшую разность энергетических уровней электрона.
- Вычислить энергию ядерной реакции:
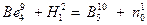
24. Вычислить энергию ядерной реакции:
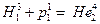
- Вычислить энергию ядерной реакции:
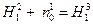
- Вычислить энергию ядерной реакции:
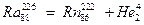
- Вычислить энергию ядерной реакции:
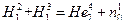
- Ядро лития , захватывая протон, распадается на две α-частицы. Написать ядерную реакцию и определить энергию, выделяющуюся при этой реакции.
- Определить энергию, выделяющуюся при образовании из протонов и нейтронов гелия массой 1 г.
- При сгорании ядерного топлива на атомной электростанции за 1 с выделяется приблизительно 28,5 МДж энергии. Сколько ядерного горючего расходует станция за сутки, если принять, что один атом урана Место для формулы.
 при делении на два осколка выделяет 200 МэВ энергии?
при делении на два осколка выделяет 200 МэВ энергии? - Образец содержит 1000 радиоактивных атомов с периодом полураспада Т. Сколько атомов останется через промежуток времени Т/2?
- Образец радиоактивного радона содержит
 радиоактивных атомов с периодом полураспада 3,825 сут. Сколько атомов распадается за сутки?
радиоактивных атомов с периодом полураспада 3,825 сут. Сколько атомов распадается за сутки?
- Сколько ядер распадается за 1 с в препарате радиоактивного изотопа иридия и сколько останется атомов этого препарата через 30,0 сут, если первоначальная его масса равна 1г.
- Сколько ядер распадается за 1 с в куске урана
 и массой 1,0 кг? Какова активность этого урана?
и массой 1,0 кг? Какова активность этого урана? - Найти период полураспада радиоактивного изотопа, если его активность за время t = 10 суток уменьшилась на 24% по сравнению с первоначальной.
36. Определить, какая доля радиоактивного изотопа 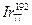 распадается в течение 6 суток.
распадается в течение 6 суток.
37. Активность некоторого изотопа за время 10 суток уменьшилась на 20%. Определить период полураспада этого изотопа.
38. Найти среднюю продолжительность жизни атома радиоактивного изотопа стронция 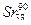 .
.
39. Счетчик α – частиц, установленный вблизи радиоактивного изотопа, при первом измерении регистрировал 1400 частиц в минуту, а через 4 часа только 400 частиц. Определить период полураспада изотопа.
40. Во сколько раз уменьшится активность препарата 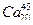 через 20 суток?
через 20 суток?
×
СПРАВОЧНЫЕ МАТЕРИАЛЫ.
| Физическая постоянная | Обозначение | Численное значение |
| Гравитационная постоянная | G | 6.67 10–11 м2/кг×с2 |
| Число Авагадро | NА | 6.02 × 1023 моль–1 |
| Газовая постоянная | R | 8.31 Дж/моль×К |
| Постоянная Больцмана | k | 1.38 × 10–23 Дж/К |
| Заряд электрона | е | 1.6 ×10–19 Кл |
| Электрическая постоянная | ε0 | 8.85 × 10–12 Ф/м |
| Магнитная постоянная | μ0 | 1.26 ×10–6 Гн/м |
| Постоянная Фарадея | F | 9.65 ×107 Кл/кг×экв. |
| Постоянная Стефана–Больцмана | σ | 5.67 ×10–8 Вт/м2×К4 |
| Постоянная Вина | с | 2.89 ×10–3 м×К |
| Постоянная Планка | h | 6.62 ×10–34 Дж×с |
| Постоянная Ридберга | R | 1.097×107 м–1 |
| Радиус первой боровской орбиты | r1 | 0.529×10–10 м |
| Энергия ионизации атома водорода | Е1 | 2.18×10–18Дж=13.6 эВ |
| Атомная единица массы | а.е.м | 1.66 ×10–27 кг |
Астрономические величины.
Средний радиус Земли 6.37 ×106 м
Средняя плотность Земли 5.5 ×103 кг/м3
Масса Земли 5.96 ×1024 кг
Радиус Солнца 6.95 ×108 м
Средняя плотность Солнца 1.4 ×103 кг/м3
Масса Солнца 1.97 ×1030 кг
Радиус Луны 1.74 ×106 м
Масса Луны 7.3 ×1022 кг
Радиус орбиты Земли 1.5 ×1011 м
Радиус орбиты Луны 3.84 ×108 м
Показатель преломления.
Алмаз – 2.42; Вода – 1.33; Лед – 1.31; Стекло – 1.52;
Кварц – 1.55; Сероуглерод –1.6;
Греческий алфавит.
| Обозначение | Название | Обозначение | Название |
| α | альфа | ν | ню |
| β | бета | ξ | кси |
| γ | гамма | ο | омикрон |
| δ | дельта | π | пи |
| ε | эпсилон | ρ | ро |
| ζ | дзета | σ | сигма |
| η | эта | τ | тау |
| θ | тета | υ | ипсилон |
| ι | иота | φ | фи |
| æ | каппа | χ | хи |
| λ | ламбда | ψ | пси |
| μ | ми | ω | омега |
ЛИТЕРАТУРА.
Основная литература и пособия
1. Трофимова Т.И. Курс физики. М.: Высшая школа, 2001.
2. Детлаф А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 2000.
3. Сборник задач по курсу общей физики: Учеб пособие:
Г. А. Загуста, Г. П. Макеева, А. С. Микулич и др.;
Под ред. М. С. Цедрика. М.: Просвещение, 1989. 271 стр.
4. Волькенштейн В. С. Сборник задач по общему курсу физики. Учебное пособие.— 11-е изд., перераб.— М.: Наука, 1989 г.
Дополнительная литература
1. Савельев И.В. Курс общей физики. 1-3 том. М.: Наука, 1978.
2. Детлаф А.А., Яворский Б.М. Справочник по физике для инженеров и студентов ВУЗов. М.: Наука, 1974.
3. Донской А.Д., Острик А.В., Острик В.М. Основные законы физики. М.: ГАСБУ, 1997.
4. Ванюшкин В.П., Донской А.Д., Черкасская А.И. Физика. М.: Методические указания и задачи для студентов-заочников. ГАСБУ, 1993
Содержание.
1. Введение._________________________________________________3
2. Механика._________________________________________________9
3. Молекулярная физика и термодинамика._______________________21
4. Электростатика. Постоянный ток. ____________________________33
5. Электромагнитизм. ________________________________________ 46
6. Оптика. __________________________________________________57
7. Физика атома и атомного ядра. ______________________________70
8. Справочные материалы. ____________________________________78
Литература. ______________________________________________82
Ф И З И К А
Учебное пособие:
Методические материалы и указания к выполнению контрольных работ
для студентов заочной формы обучения
Королев, 2017
А.Д.Сабо С.Е., Мацнев Н.П. Физика. Учебное пособие: Методические материалы и указания к выполнению контрольных работ для студентов заочной формы обучения. Королев:, 2017.- 83 с.
Рецензент: д.т.н., профессор Захаров Е.Н.
Методические рекомендации и указания составлены в соответствии с требованиями Федерального государственного образовательного стандарта высшего профессионального образования по специальностям 24.05.01 и направлениям подготовки 15.03.05, 15.03.06, 27.03.02, 27.03.04, 09.03.02, 09.03.03, 01.03.02.
Введение.
1. За время изучения курса общей физики студент–заочник должен представить на кафедру контрольные работы.
2. Контрольные задания выдаются студентам лектором потока.
3. Контрольные работы необходимо выполнять чернилами в школьной тетради, на обложке которой привести сведения по следующему образцу:
Контрольная работа по физике № __
Студент – Киселев А.В.
Группа – УТС–17
Шифр – (номер зачетной книжки).
4. Условия задач в контрольной работе надо переписать полностью без сокращений. Для замечаний преподавателя на страницах тетради оставлять поля.
5. В конце контрольной работы указать, каким учебником или учебным пособием студент пользовался при изучении физики (название учебника, автор, год издания). Это делается для того, чтобы рецензент в случае необходимости мог указать, что следует студенту изучить для завершения контрольной работы.
6. Если контрольная работа при рецензировании не зачтена, студент обязан представить ее на повторную рецензию, включив в нее те задачи, решения которых оказались неверными. Повторную работу необходимо представить вместе с не зачтенной работой.
7. Зачтенные контрольные работы предъявляются экзаменатору. Студент должен быть готов, во время экзамена (зачета) дать пояснения по существу решения задач, входящих в контрольные работы.
8. Решения задач следует сопровождать краткими, но исчерпывающими пояснениями. В тех случаях, когда возможно, дать рисунок, схему.
9. Обозначения физических величин в условии задачи, на рисунке и в ходе решения должны быть одинаковыми.
10. Решать задачу надо в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин.
11. После получения расчетной формулы для проверки правильности ее следует подставить в правую часть формулы вместо символов величин обозначения единиц этих величин, произвести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине. Если такого соответствия нет, то это означает, что задача решена неверно.
12. Числовые значения величин при подстановке их в расчетную формулу следует выражать только в единицах СИ. В виде исключения допускается выражать в любых, но одинаковых единицах числовые значения однородных величин, стоящих в числителе и знаменателе дроби и имеющих одинаковые степени.
Все необходимы для решения задачи значения приведены в задаче и приложениях к данному задачнику.
13. При подстановке в расчетную формулу, а также при записи ответа числовые значения величин следует записывать как произведение десятичной дроби с одной значащей цифрой перед запятой на соответствующую степень десяти. Например, вместо 0,00129 кг записать 1,29*10-3 кг т.п.
14. Вычисления по расчетной формуле надо проводить с соблюдением правил приближенных вычислений (см."Задачник по физике" А. Г. Чертов, А.А.Воробьев «Приложение о приближенных вычислениях».) Как правило, окончательный ответ следует записывать с тремя значащими цифрами. Это относится и к случаю, когда результат получен с применением калькулятора.
Дата: 2018-12-28, просмотров: 632.