В результате измерений получаются приближенные числа, последняя цифра которых точно не определена (ее называют сомнительной цифрой). Например (32.3±0.1) м, (2.50±0.02) кг и т.д.

Умножая, складывая, возводя в степень числа, можно получить любое количество десятичных знаков, но не все из них несут полезную информацию. Значащие цифры – это все цифры числа, начиная с первой слева, отличной от нуля, и до последней, правильность которой с какой то надежностью можно гарантировать. Эта последняя цифра называется сомнительной, и ее разряд совпадает с разрядом абсолютной погрешности. Все цифры, следующие за сомнительной, не являются значащими и должны быть отброшены с округлением.

Не являются значащими нули слева от первой значащей цифры и все нули справа, полученные в результате округления. Эти нули указывают порядок числа и должны быть вынесены в отдельный множитель. Так, например, вместо 0.0014000 надо писать 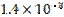, а вместо 37000 – 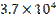, если в числах по две значащих цифры. Нуль в конце числа может быть значащим, но тогда это надо специально указывать. Запись приведенных чисел с тремя значащими цифрами выглядит так:  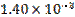и .

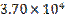Численные значения величин, которыми приходится оперировать при решении физических задач, являются приближенными. Поэтому, при вычислениях необходимо соблюдать следующие правила:

1. Достаточно производить вычисления с числами, содержащими не более знаков, чем в исходных данных, так как с помощью вычислений невозможно получить результат более точный, чем исходные данные.

2. При сложении и вычитании чисел, имеющих разную точность, более точное округляется до менее точного. Например: 9.6 + 0.176 = 9.6 + 0.2 = 9.8; 100.83 – 0.4 = 100.8 – 0.4 = 100.4.

3. При умножении и делении результат следует округлять так, чтобы он содержал столько значащих цифр, сколько их имеет сомножитель с наименьшим числом значащих цифр. Например: 342×378=129×10³; 0.352:0.301=0.117.

4. При извлечении корня результат должен иметь столько значащих цифр, сколько их имеет подкоренное выражение. Например: .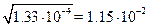

5. При вычислении сложных выражений выполняются правила в зависимости от производимых действий.

6. Если угол α<0.2 радиан, то sin α = tg α = α.

Механика

Основные формулы.

Кинематическое уравнение движения материальной точки (центра массы твёрдого тела) вдоль оси :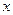

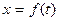
где 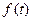 –некоторая функция времени.

Проекция средней скорости на ось :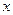

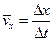
Средняя скорость движения:

=

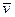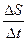
где 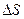- путь, пройденный точкой за интервал времени .

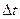Путь 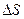, в отличие от разности координат 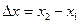, не может убывать и принимать отрицательные значения, т.е. .

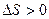Проекция мгновенной скорости на ось :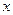

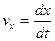
Проекция среднего ускорения на ось :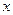

=

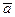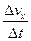
Проекция мгновенного ускорения на ось :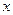

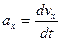
Кинематическое уравнение движения материальной точки по окружности ( ):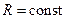

,    

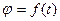Модуль угловой скорости:

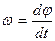
Модуль углового ускорения:

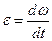
Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:

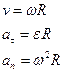
где 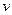 - модуль линейной скорост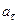и;  и 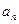- модули тангенциального и нормального ускорений; 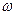– модуль угловой скорости; 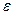- модуль углового ускорения; R- радиус окружности.

Модуль полного ускорения:

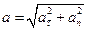    или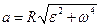  

Угол между полным a и нормальным a 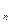 ускорениями:

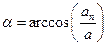
Кинематическое уравнение гармонических колебаний материальной точки:

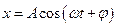
где 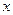 - смещение; A– амплитуда колебаний;  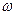- угловая или циклическая частота;  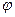-начальная фаза.

Скорость и ускорение материальной точки, совершающей гармонические колебания:

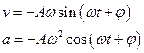
Сложение гармонических колебаний одного направления и одинаковой частоты:

-  амплитуда результирующего колебания                          

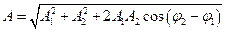
- начальная фаза результирующего колебания

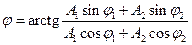
Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях:

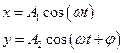
a) 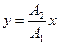   если разность фаз ;

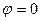б) 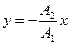   если разность фаз ;

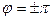в) 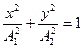  если разность фаз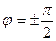

Уравнение плоской бегущей волны:

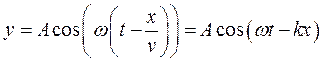
где 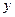 - смещение любой из точек среды с координатой  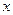в момент 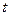;  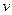- скорость распространения колебаний в среде,  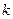– волновое число.

Связь разности фаз 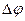 колебаний с расстоянием  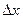между точками среды, отсчитанным в направлении распространения колебаний:

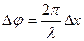
где 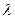 - длина волны.

Импульс материальной точки массой m, движущейся со скоростью ,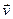

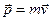
Второй закон Ньютона:

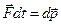
где 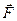 - результирующая сила, действующая на материальную точку.