МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ДНР
ГОУ ВПО «ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ»
КАФЕДРА «ЭКОНОМИЧЕСКАЯ ТЕОРИЯ И ИНФОРМАЦИОННО-СТОИМОСТНОЙ ИНЖИНИРИНГ»
УТВЕРЖДАЮ
Зав. кафедрой
"Экономическая теория и информационно-
стоимостной инжиниринг"
___________ / ______________
«____» _______________2016 г.
КОНСПЕКТ ЛЕКЦИЙ
"Теория статистики"
для направления
38.03.02 "Менеджмент"
Макеевка
2016
СОДЕРЖАНИЕ
| Содержательный модуль 1. Теоретические основы статистики…… | 3 |
| Тема 1. Методологические основы статистики………………………….. | 3 |
| Тема 2. Статистическое наблюдение……………………………………... | 10 |
| Тема 3. Сводка, группировка статистических данных………………….. | 17 |
| Тема 4. Представление статистических данных: таблицы, графики, карты………………………………………………………………………..… | 24 |
| Тема 5. Обобщающие статистические показатели………………………. | 32 |
| Содержательный модуль 2. Статистические методы исследования вариации и динамика показателей…………………………………….. | 40 |
| Тема 6. Анализ рядов распределения…………………………………... | 40 |
| Тема 7. Анализ концентрации, дифференциации распределения……. | 50 |
| Тема 8. Статистические методы измерения взаимосвязи……………….. | 60 |
| Содержательный модуль 3. Методы исследования показателей статистического анализа социально - экономических явлений……. | 71 |
| Тема 9. Выборочное наблюдение…………………………………………. | 71 |
| Тема 10 . Анализ интенсивности динамики……………………………… | 84 |
| Тема 11. Анализ тенденций развития…………………………………….. | 89 |
| Тема 12. Индексы…………………………………………………..……... | 95 |
| Литература………………………………………………………………….. | 104 |
МОДУЛЬ 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СТАТИСТИКИ
ТЕМА 1. МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ СТАТИСТИКИ.
1. Статистика как наука.
2. Предмет статистики и ее категории.
3. Методология статистики и ее задачи
Статистика как наука.
Статистика предоставляет человечеству разнообразную информацию, осуществляет учет многих явлений и процессов (численность мужского и женского населения, количество земельных угодий, сырья, ресурсов, государственного дохода и т.д.).
Термин «статистика» произошел от латинского слова «статус» (status), который использовался вначале в значении «сумма знаний о государстве». В науку термин «статистика» ввел ученый Готфрид Ахенваль в 1746 году, предложив заменить название курса «Государствоведение», преподававшегося в университетах Германии, на «Статистику», положив начало развитию статистики как науки и учебной дисциплины. Несмотря на это, статистический учет велся намного раньше: проводились переписи населения в Древнем Китае, осуществлялось сравнение военного потенциала государств, велся учет имущества граждан в Древнем Риме и пр. При углублении общественного разделения труда, развития производства увеличивалось количество учитываемых факторов и как следствие количество рассчитываемых показателей.
Статистика как наука развивалась по нескольким направлениям: описательному, математическому и математико-статистическому.
Представители описательной школы (Герман Конринг, Готфрид Ахенваль) своей задачей считали описание достопримечательностей государства: территории, населения, политического устройства.
Представители математического направления или школы «политической арифметики» (Уильям Петти, Джон Граунт) выявляли на основе большого числа наблюдений различные закономерности и взаимосвязи в изучаемых явлениях.
Математико-статистическое направление возникло в начале ХІХ века. Представители этого направления (К. Пирсон, А.Кетле, Р.Фишер, М.Митчел) использовали в статистических исследованиях математические методы.
Особенностью статистики является то, что статистические данные предоставляются в количественной форме, т.е. статистика говорит языком цифр, которые отображают общественную жизнь в ее разнообразии.
На современном этапе под статистикой понимают и направление практической деятельностью, и экономическую науку, и учебную дисциплину по изучению способов сбора, обработки и анализа данных о массовых социально-экономических явлениях и процессах.
Как направление практической деятельности статистика занимается сбором, накоплением, обработкой цифровых данных, которые характеризуют экономику, население, культуру, образование и другие явления в жизни общества.
Также статистикой называют науку, т.е. отрасль знаний, которая изучает массовые явления в жизни общества с их количественной стороны.
Основой для изучения массовых явлений является закон больших чисел, сущность которого состоит в том, что количественные закономерности массовых явлений отчетливо проявляются лишь в достаточно большом их числе. Т.е. каждое единичное явление является случайным (т.е. оно может быть или не быть), но при объединении большого количества таких явлений в общей характеристике их массы случайность тем больше уменьшается, чем больше объединяется единичных явлений (например, урожайность на одном конкретном поле может быть больше или меньше, даже если оно удобрено лучше другого, а урожайность в целом большого количества хорошо удобренных полей будет выше, чем большого количества полей хуже удобренных).
Статистическая отчетность.
Особая форма организации сбора данных государственной статистикой о деятельности хозяйствующих субъектов, которые обязаны заполнять документы-бланки, называемые формами статистической отчетности, содержащие перечень определенных показателей, сведений, характеризующих ту или иную хозяйственую единицу и результаты ее деятельности, заполняемый на основе данных опертивного или бухгалтерского учета и представляемые в государственные статистические органы для дальнейшего обобщения. Каждая форма отчетности имеет шифр и название. В соответствии со сроками представления отчетность бывает суточная (ежедневная), недельная, месячная, квартальная, полугодовая и годовая. Все эти виды отчетности, кроме годовой, объединяют одним названием – текущая отчетность.
Наблюдение через регистры.
Сравнительно новая форма организации статистического наблюдения, основанная на применении компьютерных технологий. Регистр – это поименованный и постоянно уточняемый перечень тех или иных единиц наблюдения, созданный для непрерывного длительного статистического наблюдения за определенной совокупностью, в котором содержится информация о каждой единице совокупности (например, ЕГРПО – Единый государственный регистр предприятий и организаций, реестр населения.).
Все эти 3 организационные формы статистического наблюдения не противостоят, а дополняют друг друга, позволяя более глубоко и всесторонне изучать отдельные явления и процессы общественной жизни.
Статистическое наблюдение можно классифицировать по следующим признакам:
1. По времени регистрации фактов:
- непрерывное (текущее), которое ведется систематически, т.е. регистрация фактов производится по мере их совершения (например, ЗАГС);
- периодическое, которое повторяется через определенные равные промежутки времени (например, перепись населения);
- единовременное, которое производится по мере надобности без соблюдения определенной периодичности (например, оценка и переоценка основных фондов).
2. По охвату единиц совокупности:
- сплошное, при котором исследованию подвергаются все единицы изучаемой совокупности;
- несплошное, при котором исследованию подвергается только часть единиц изучаемой совокупности, отобранная определенным образом.
При несплошном наблюдении используются:
-анкетный способ (исследуются осредненные показатели и распространяются на всю совокупность);
- метод основного массива (исследуются наиболее крупные единицы изучаемого явления);
- выборочный метод (основой является случайный отбор, а результат гарантируется с определенной вероятностью);
- монографический метод (подвергаются исследованию либо самые лучшие (худшие) единицы, либо представители новых типов и результаты переносятся на всю совокупность);
- мониторинг.
Основанием для регистрации фактов могут служить либо документы, либо высказанное мнение, либо хронометражные данные. В связи с этим различают наблюдение:
- непосредственное (сведения, подлежащие фиксации, определенным образом измеряются, взвешиваются для единиц объекта наблюдения);
- документальное (базируется на использовании документов – бухгалтерских документов, годовых отчетов и т.д.);
- опрос (сведения получают устно или письменно со слов опрашиваемых лиц).
Опрос может быть:
- экспедиционным (осуществляется специально подготовленными лицами);
- корреспондентским (необходимые сведения предоставляют лица, которые добровольно изъявили желание ответить на поставленные в анкетах вопросы);
- в форме саморегистрации (регистрация фактов самими респондентами после предварительного инструктажа).
Задания статистических группировок, их виды
В целом, статистическая группировка является основным элементом статистической сводки и представляет собой метод исследования массовых общественных явлений путем выделения и ограничения однородных групп, через которые раскрываются существенные черты и особенности состояния и развития всей совокупности. Т.е. при статистической группировке производится распределение совокупности на группы и подгруппы по определенным существенным признакам, что позволяет определить связь между группами, типами и формами явлений.
Кроме того, рассматривая изменение признаков в группах можно изучить зависимость результативного признака от факторного, который положен в основу группировки. Факторный признак – это признак, который отображает причину, а признак, который отображает следствие называется результативным.
Признаки единиц совокупности, которые принимают разные количественные или качественные значения в отдельных единицах совокупности называют вариационными признаками. Например, предприятие как единица совокупности предприятий в промышленности характеризуется:
- принадлежностью к определенному сектору (частному или государственному);
- принадлежностью к определенной отрасли производства;
- определенной численностью работников;
- наличием различных основных фондов.
Группировочный признак – это вариационный признак, поэтому говорят, что группы создаются на основе вариации признаков.
По форме выражения признаки группировок бывают:
- атрибутивные (качественные) (например, принадлежность к определенному сектору, пол, образование, специальность);
- вариативные (количественные) (например, численность работников, стоимость продукции, сумма заработной платы).
С помощью группировок решаются следующие задачи:
1. выделение социально-экономических типов;
2. изучение структуры социально-экономических явлений;
3. выявление связи между явлениями.
Для решения этих задач используются типологические, структурные, аналитические и комбинационные группировки.
С помощью типологических группировок выделяют наиболее характерные группы, типы явлений, из которых состоит неоднородная статистическая совокупность. Эти группировки используют при изучении распределения предприятий по формам собственности, при группировках населения по общественным группам (работающие, школьники, пенсионеры), работников по уровню образования. Пример типологической группировки представлен в табл. 3.1.
Таблица 3.1.
Распределение населения страны, занятого в различных сферах экономики, %
| Сфера деятельности | 2005 | 2015 |
| Всего занято, в том числе: | 100 | 100 |
| в сфере материального производства | 80 | 73,8 |
| в непроизводственной сфере | 20 | 26,2 |
Структурные группировки характеризуют распределение качественно однородной совокупности по определенному признаку. С помощью структурных группировок изучается состав населения по возрасту, полу, национальностью, состав семей по количеству детей, доходов, состав работников по профессиям, стажу работы. Пример структурной группировки представлен в табл. 3.2.
Таблица 3.2.
Распределение населения региона по совокупному доходу на душу населения
| Среднемесячный доход на душу населения | Численность населения, тыс.р. | Структура, % |
| До 1000 | 7 | 14 |
| 1001-2000 | 24 | 48 |
| 2001-3000 | 4 | 8 |
| 3001-4000 | 12 | 24 |
| Более 4000 | 3 | 6 |
| Всего | 50 | 100 |
Типологические группировки отличаются от структурных целью исследования, а по форме они одинаковы.
Выявление и изучение взаимосвязей между признаками осуществляются на основе аналитических группировок (например, изучение взаимосвязи между уровнем квалификации и уровнем заработной платы). Аналитические группировки проводятся по факторному признаку и в каждой группе, как правило, определяется средняя величина результативного признака (табл.3.3).
Таблица 3.3.
Схема аналитической группировки
| Факторный признак (Хі) | Количество единиц совокупности (Fi) | Среднее значение результативного признака (Уі) |
| Х1 | F 1 | У1 |
| Х2 | F 2 | У2 |
| Всего | F |
В комбинационных группировках производится разделение совокупности на группы по двум или болем признакам. При этом группы, образованные по одному признаку, разбиваются на подгруппы по другому признаку. Такие совокупности дают возможность изучить структуру совокупности по нескольким признакам одновременно.
Статистические графики.
Наглядное изображение результатов наблюдения и группировок социально-экономических явлений и процессов может быть представлено на графиках.
Статистический график – это масштабное условное изображение статистических данных с помощью линий, геометрических фигур и других наглядных средств.
В статистическом графике выделяют основные элементы:
- поле графика (место на котором он выполняется);
- графический образ (символические знаки, с помощью которых изображаются статистические данные);
- пространственные ориентиры (задаются координатной сеткой или контурными линиями и разделяют поле графика на части);
- масштабные ориентиры (предоставляют графическим образам количественную значимость, которая передается с помощью системы масштабных шкал);
- экспликацию графика (пояснения его содержания, содержит в себе заголовок графика, пояснения масштабных шкал, пояснения отдельных элементов графического образа).
Статистические графики отличаются большим разнообразием. Их можно разделить на 2 группы:
- диаграммы;
- статистические карты.
На диаграммах, как правило, статистические данные изображаются с помощью геометрических знаков, линий и фигур.
В зависимости от способа построения выделяют следующие виды диаграмм:
- линейные;
- радиальные;
- секторные;
- столбиковые;
- фигурные и др.
С помощью линейных диаграмм чаще всего отображают динамику (развитие явлений во времени).
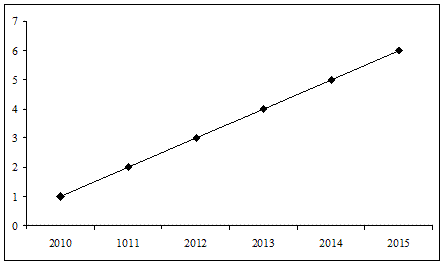
По горизонтальной оси изображаются временные интервалы, по вертикальной – числовые значения показателя, линия характеризует изменение исследуемого явления во времени.
Если по оси абсцисс отложить ранжированные значения варьирующего признака, а по оси ординат нанести шкалу для выражения величины частот и полученные на пересечении абсцисс и ординат точки соединить прямыми линиями, то получаем ломанную линию, которую называют полигоном частот.
Радиальные диаграммы используют для изображения явлений, которые периодически изменяются (сезонные колебания). Для их построения используют полярную систему координат. Окружность разделяют на 12 равных частей, каждая из которых означает определенный месяц. На радиусе, начиная из центра, в масштабе откладывают отрезки, которые отображают каждый месяц какой-то признак. Окончания отрезков соединяют между собой и получают замкнутую фигуру – двенадцатигранник, которая характеризует сезонные колебания исследуемого явления.
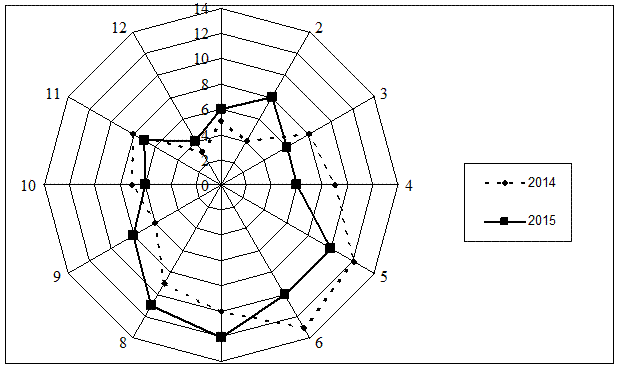
Рис.4.2. Потребление электроэнергии в регионе по месяцам
Секторные диаграммы характеризуют структуру явления. Для построения круг разделяется радиусами на секторы, площади которых пропорциональны частям исследуемого явления в общем объеме изображенного круга (100 %).
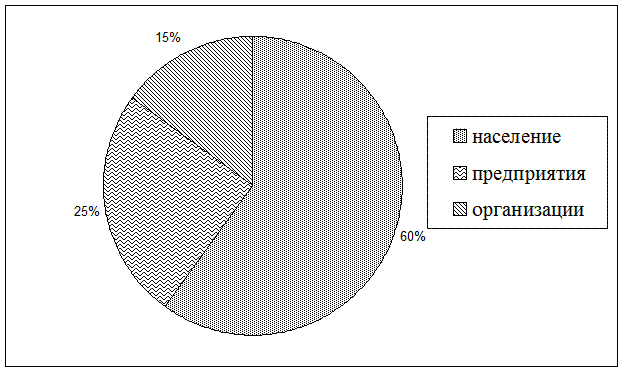
Рис. 4.3. Структура потребителей услуг ЖКХ
Столбиковые диаграммы используются для наглядного сопоставления изучаемого явления во времени или в пространстве.
Чаще всего в виде столбиковых диаграмм изображается интервальный ряд. Основания столбиков, расположенные по оси абсцисс, – это интервалы значений варьирующего признака, а высоты столбиков – частоты, соответствующие масштабу по оси ординат. Графическое изображение интервального ряда приведено на рис.4.Ошибка! Источник ссылки не найден.. Диаграмма такого типа называется гистограммой.
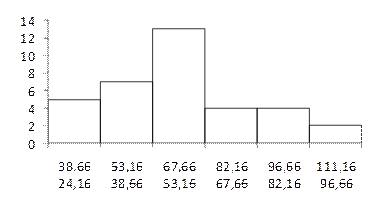
Рис. 4.4. Распределение предприятий в выборке по величине основных фондов
Фигурные диаграммы используют обычно в рекламных целях. При их построении статистические данные изображаются рисунками-символами, площади которых пропорциональны величинам соответствующих признаков.
К статистическим картам относятся картограммы и картодиаграммы.
Картограммы – это изображения определенного признака на схематической географической карте разными штриховками и окрашиваниями.
Картодиаграмма представляет собой объединение схематической географической карты с одной из диаграмм. Статистические показатели изображаются в виде столбиков, квадратов, треугольников и т.д.
Средние величины.
Средняя величина в статистике – это обобщающая характеристика количественно и качественно однородной совокупности в определенных условиях. Среднее определяется по какому-либо признаку и проявляется в результате действия закона больших чисел, когда в массовых совокупностях индивидуальные отклонения от типичного уровня взаимопогашаются. Т.е. среднее позволяет заменить множество значений показателей одним типичным, что значительно упрощает последующий анализ явлений.
Средняя применяется в статистических исследованиях для оценки сложившегося уровня явления, для сравнения между собой нескольких совокупностей по одному и тому же признаку, для исследования динамики развития изучаемого явления во времени, для изучения взаимосвязей явлений.
Главное значение средних величин состоит в их обобщающей функции, то есть замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений.
Виды средних величин различаются прежде всего тем, какое свойство, какой параметр исходной варьирующей массы индивидуальных значений признака должен быть сохранен неизменным.
Выделяют следующие виды средних величин:
1. Средняя арифметическая.
2. Средняя гармоническая.
3. Средняя квадратическая.
4. Средняя геометрическая.
5. Средняя хронологическая.
Для несгруппированных данных используют средние простые, для сгруппированных (которые представлены в виде рядов распределения) – средние взвешенные.
1. Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Иначе можно сказать, что средняя арифметическая величина – среднее слагаемое. При ее вычислении общий объем признака распределяется поровну между всеми единицами совокупности.
Таким образом, средняя арифметическая простая рассчитывается как сумма отдельных значений признака X, деленная на число этих значений N:
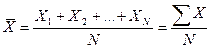 .
.
Если изучаемая совокупность велика, исходная информация чаще представляет собой ряд распределения или группировку, при этом используется формула средней арифметической взвешенной:
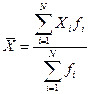 ,
,
где Xi - значения признака в каждой группе (варианта);
fi - повторяемость признака (частота);
i – число групп.
Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, то есть исходят из предположения о равномерном распределении единиц совокупности по интервалу значений признака.
2. Средняя гармоническая взвешенная применяется когда статистическая информация не содержит частот f по отдельным вариантам Xi совокупности, а представлена как их произведение Xf. Для получения формулы обозначим Xf = w, откуда f = w / X:
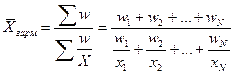 .
.
В тех случаях, когда вес каждого варианта w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:
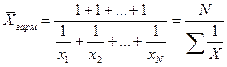 .
.
3. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменную сумму квадратов исходных величин, то средняя будет являться средней квадратической величиной. Формула средней квадратической простой имеет вид:
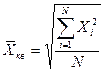 .
.
Средняя квадратичная используется, когда значения признака представлены в виде отклонений от нормы или стандарта.
Формула средней квадратической взвешенной:
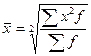 .
.
Главной сферой применения квадратической средней является измерение вариации признака в совокупности.
4. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить среднюю геометрическую величину. Средняя геометрическая простая имеет следующий вид:
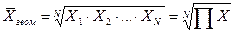 .
.
Основное применение средняя геометрическая находит при определении средних относительных изменений. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения признака, который качественно был бы равноудален как от максимального, так и от минимального значения признака.
5. Средняя хронологическая используется преимущественно в бухгалтерском учете для определения среднегодовых остатков материальных ценностей.
Все рассмотренные выше виды средних величин принадлежат к общему типу степенных средних, имеющему следующий вид:
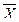 =
= 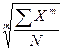 .
.
При m = 1 получаем среднюю арифметическую; при m = 2 – среднюю квадратическую; при m = 0 – среднюю геометрическую; при m = –1 – среднюю гармоническую. Чем выше показатель степени m, тем больше значение средней величины (если индивидуальные значения признака варьируют). Это называется правилом мажорантности средней.
МОДУЛЬ 2. СТАТИСТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ВАРИАЦИИ И ИЗМЕРЕНИЯ ВЗАИМОСВЯЗЕЙ
Понятие рядов распределения
Отдельный вид группировок в статистике - ряды распределения, которые являются наипростейшим способом обобщения статистических данных.
Ряд распределения – это группировка, которая характеризует состав (структуру) явления в данный период времени.
В зависимости от того, какой признак (количественный или качественный) положен в основу группировки, ряды распределения бывают:
- атрибутивные (качественные) (например, распределение населения по возрасту, занятости, национальности, профессии и т.д.);
- вариационные (количественные).
Вариационные ряды распределения бывают дискретными и интервальными.
Дискретный ряд – это ряд, в котором варианты (отдельные значения группировочного признака) выражены целыми числами (табл. 6.1.).
Таблица 6.1.
Распределение работников по тарифным разрядам
| Тарифный разряд | Количество работников, чел. |
| 1 | 10 |
| 2 | 20 |
| 3 | 40 |
| 4 | 60 |
| 5 | 50 |
| 6 | 20 |
| Итого | 200 |
Интервальный ряд распределения – ряд, в котором значения признака заданы в виде интервалов (табл.6.2.).
Таблица 6.2.
Распределение коммерческих банков по величине капитала
| Размер капитала, млн.р. | Количество банков, ед. |
| 3-6 | 9 |
| 6-9 | 13 |
| 9-12 | 4 |
| Итого | 26 |
Ряд распределения состоит из двух элементов: вариант и частот.
Варианты – числовые значения количественного признака в группировке (они могут быть абсолютными, относительными, отрицательные, положительные) (первая графа таблицы).
Частоты – числа, которые показывают, сколько раз повторяются отдельные значения вариант (выражаются в виде коэффициентов или процентов (доля)). Накопленную частоту называют кумулятивной.
Ранжированным рядом распределения называют ряд, в котором значения признака располагаются в возрастающем (снижающемся) порядке и расчет ведется по группам.
Графически дискретный ряд изображается в виде полигона, а вариационный ряд с равными интервалами – в виде гистограммы. Ряд распределения с неравными интервалами также представляется в виде гистограммы, которая строится на основе тесноты распределения.
Теснота распределения – количество элементов совокупности, которое приходится на единицу ширины интервала группировочного признака. Например, по количеству ученических мест 400 школ области находятся в интервале от 800-1000. Тогда теснота распределения составляет 400/(1000-800) =2.
Показатели вариации
После определения средней величины встает вопрос, в какой мере индивидуальные значения признака отличаются между собой и от средней. Для этого определяют показатели вариации.
Вариацией признака называют разницу в числовых значениях признаков единиц совокупности и их колебания вокруг средней величины, которая характеризует совокупность. Чем меньше вариация, тем более однородной является совокупность и более надежной (типовой) – средняя величина.
К основным абсолютным и относительным показателям, характеризующим вариацию относятся:
- размах вариации;
- среднее линейное отклонение;
- коэффициент осцилляции;
- дисперсия;
- стандартное среднее квадратическое отклонение;
- коэффициент вариации.
Размах вариации – это разница между наибольшим 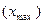 и наименьшим
и наименьшим 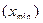 значениями признака:
значениями признака:
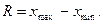
Среднее линейное отклонение – это средний модуль отклонений индивидуальных значений признака от их средней величины:
- для несгруппированных данных 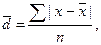
- для сгруппированных данных 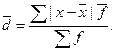
Коэффициент осциляции – это отношение размаха вариации к среднему значению признака:
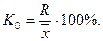
Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от средней величины:
- для несгруппированных даннях 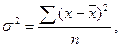
- для сгруппированных данных 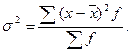
Среднее квадратическое отклонение – это обобщающая характеристика абсолютних размеров вариации признака в совокупности.Определяется как корень квадратный из дисперсии:
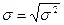
Среднее квадратическое отклонение всегда выражается в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.) и является абсолютной мерой вариации.
Чем меньше среднее квадратическое отклонение, тем более типовой является средняя и тем более однородной является совокупность.
Коэффициент вариации является относительной мерой вариации и позволяет сравнивать степень вариации признаков в рядах вариации с разным уровнем средних. Рассчитывается как отношение среднего квадратического отклонения от средней величины:
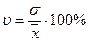 .
.
Если коэффициент вариации <33 %, то такая совокупность считается однородной.
Дисперсионный анализ
Основной целью дисперсионного анализа является выявление на основе величины общей дисперсии влияния отдельных факторов на вариацию признака. Для оценки доли вариации, обусловленной тем или иным признаком, совокупность разделяют на группы по тому признаку, свойства которого исследуются. Это позволяет разложить общую дисперсию на 2 дисперсии, из которых одна часть вариации определяется влиянием фактора, который положен в основу группировки, а вторая – вариацией всех факторов, кроме того, который изучается. Т.е. соответственно с правилом сложения дисперсий, если данные представлены в виде аналитической группировки, определяют общую, межгрупповую, внутригрупповую дисперсии.
Общая дисперсия характеризует вариацию признака в статистической совокупности в результате влияния всех факторов.
Общая дисперсия для сгруппированных данных определяется по формуле:
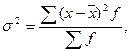
для несгруппированных даннях:
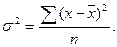
Кроме того, применяются два упрощенных способа расчета общей дисперсии:
1. Если варианты выражены небольшими числами, дисперсия определяется как разность средних:
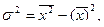
2. Если варианты выражены большими числами, то применяют способ моментов:
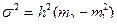 ,
,
где m1 – момент первого порядка;
m2 – момент второго порядка.
Межгрупповая дисперсия показывает уровень отклонения групповых средних от общей средней, т.е. характеризует влияние фактора, положенного в основу группировки:
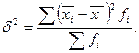
Внутригрупповая дисперсия характеризует вариацию признака в средине каждой группы статистической группировки:
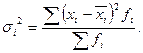
Средняя из внутригрупповых дисперсий определяется следующим образом:
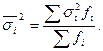
Связь между общей дисперсией, средней из групповых и межгрупповой дисперсиями можно проследить с помощью правила сложения дисперсий:
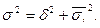
Сущность связи между признаками характеризует коэффициент детерминации, который рассчитывается как отношение межгрупповой дисперсии к общей дисперсии:
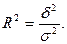
Эмпирическое корреляционное отношение – это корень квадратный из коэффициента детерминации:
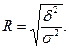
Корреляционное отношение характеризует степень приближения связи к функциональной, т.е. тесноту корреляционной зависимости и колеблется от 0 до 1.
Наряду с вариацией индивидуальных значений признака вокруг средней может наблюдаться и вариация индивидуальных долей признака вокруг средней доли. Такое изучение вариации достигается посредством вычисления и анализа следующих видов дисперсий:
- внутригрупповая: 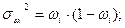
- средняя из внутригрупповых дисперсий: 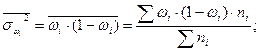
- межгрупповая: 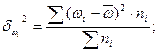
- общая: 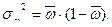
При этом 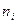 - численность единиц в отдельных группах;
- численность единиц в отдельных группах;
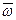 - доля изучаемого признака во всей совокупности, которая определяется по формуле:
- доля изучаемого признака во всей совокупности, которая определяется по формуле: 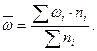
Регрессионный анализ.
Изучение корреляционной связи начинается с регрессионного анализа, который решает проблему установления формы связи или вида уравнения регрессии и определения параметров уравнения регрессии.
Различают уравнения простой (парной) регрессии (когда один х соответствует у) и множественной (многофакторной) регрессии (когда результативный признак у связан с несколькими факторными признаками х).
Уравнение регрессии показывает, как в среднем изменяется у при изменении какого-либо х і и имеет вид:
У(х) = f(х 1 ,х 2 … …х n ).
Наиболее часто для характеристики корреляционной связи используют такие вид уравнений парной регрессии:
- линейное 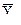 = а0 + a1 x;
= а0 + a1 x;
- гиперболическое 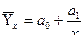 ;
;
- параболическое 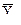 = а0 + а1 x + а1 x2 і т.д.
= а0 + а1 x + а1 x2 і т.д.
где а0, а1 – параметры уравнений регрессии, которые необходимо определить.
Параметр а0 показывает усредненное влияние на результативный признак факторов, которые не учтены.
Параметр а1 показывает насколько изменяется в среднем значение результативного признака при увеличении факторного признака на единицу.
Параметры в уравнениях регрессии определяются методом наименьших квадратов, суть которого в минимизации суммы квадратов отклонений фактических значений результативного показателя от расчетных значений.
Система нормальных уравнений для нахождения параметров линейной регрессии методом наименьших квадратов имеет такой вид:
па0 + а1 x= у;
а0 x + а1 x2 = xу,
где n – объем исследуемой совокупности (число единиц наблюдения).
Например, имеются данные, характеризующие деловую активность акционерных обществ закрытого типа (АОЗТ): прибыль (млн. р.) и затраты на 1 р. произведенной продукции (коп). (табл.8.1).
Предположим наличие линейной зависимости между анализируемыми признаками. Система нормальных уравнений для данного примера имеет вид:
па0 + а1 x= у;
а0 x + а1 x2 = xу,
Подставив данные, рассчитанные в табл.8.1. получим:
6а0 + 502а1 = 4466;
502 а0 + 42280 а1 = 362404.
Таблица 8.1
Расчетные данные для определения параметров линейного уравнения регрессии
| № | Затраты на 1 р. произведенной продукции, коп. , х | Прибыль, тыс. р., у | x2 | ху | __ x |
| 1 2 3 4 5 6 | 77 77 81 82 89 96 | 1070 1001 789 779 606 221 | 5 929 5 929 5 561 6 724 7 921 9 216 | 82 390 77 077 63 909 63 878 53 934 21 216 | 1 016 1 016 853 812 527 242 |
| Итого | 502 | 4 466 | 42 280 | 362 404 | 4 466 |
Решив систему уравнений получим: а0 = 4153,88; а1 = - 40,75
Таким образом, Ух = 4153,88 - 40,75x.
Если связь между признаками х и у является криволинейной и описывается уравнением параболы второго порядка:
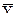 = а0 + а1 x + а2 x2
= а0 + а1 x + а2 x2
задача сводится к определению неизвестных параметров: а0, а1, а2, а система нормальных уравнений имеет вид:
па0 + а1 x + а2 x2 = у;
а0 x+ а1 x2 + а2 x3 = уx;
а0 x2 + а1 x3 + а2 x4 = уx2.
Оценка обратной зависимости между х и у, когда при увеличении (уменьшении) х уменьшается (увеличивается) значение результативного признака у, может быть осуществлена на основе уравнения гиперболы:
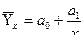 .
.
Систему нормальных уравнений для нахождения параметров гиперболы можно представить следующим образом:
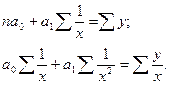
Наиболее сложным этапом, который завершает регрессионный анализ, является интерпретация уравнения, т.е. перевод его с языка статистики и математики на язык экономиста.
С целью расширения возможностей экономического анализа используется коэффициент эластичности, который определяется по формуле:
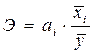 ,
,
где xі - среднее значение соответствующего факторного признака;
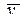 - среднее значение результативного признака;
- среднее значение результативного признака;
аі - коэффициент регрессии при соответствующем факторном признаке.
Коэффициент эластичности показывает, на сколько процентов в бреднем изменится значение результативного признака при изменении факторного признака на 1 %.
Корреляционный анализ.
После выбора вида уравнения регрессии и нахождения его параметров приступают к оценке тесноты и значимости (существенности) связи.
Тесноту святи оценивают с помощью коэффициентов детерминации, корреляции (корреляционного отношения).
Коэффициент детерминации показывает, в какой степени вариация результативного признака у определяется вариацией факторного признака х. Он используется как при линейной, так и при нелинейной связи между признаками и в случае парной регрессии рассчитывается по формуле:
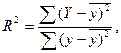
где у – фактические значения результативного признака;
У – теоретические значения результативного признака (по линии регрессии).
Коэффициент детерминации принимает значения от 0 до 1. Чем ближе он к одинице, тем теснее связь между признаками; если коэффициент детерминации равен 0 линейная связь между показателями отсутствует; если равен 1 - не существует корреляционной связи между признаками.
Коэффициент корреляции (корреляционное отношение) показывает насколько значительным является влияние фактора х на у и рассчитывается по формуле:
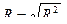
Он находится в диапазоне от 0 до1; чем ближе к единице, тем теснее корреляционная связь между признаками.
В случае линейной связи между х и у линейный коэффициент корреляции рассчитывается по формуле:
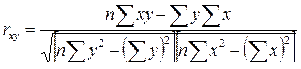
Линейный коэффициент корреляции изменяется в пределах от -1 до 1: -1 r 1.
После установления тесноты связи дают оценку значимости связи между признаками. Под термином «значимость связи» понимают оценку отклонений выборочных переменных от своих значений в генеральной совокупности с помощью статистических критериев. Оценку значимости связи осуществляют с использованием F-критерия Фишера и t-критерия Стьюдента.
Для парной регрессии (линейной и нелинейной) F-критерий Фишера рассчитывается по формуле:
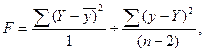
где 1, (n-2) – число степеней свободы числителя и знаменателя зависимости.
«Степень свободы» - целое число, которое показывает сколько независимых элементов информации в переменных у необходимо для суммы квадрата (это поясняет соответствующую дисперсию: общую, среднюю из групповых, межгрупповую).
Теоретическое значение F сравнивают с табличным (критическим) значением F табл, которое выбирают из справочных математических таблиц F-критерия Фишера в зависимости от степеней свободы 1, (n-2) и принятого уровня значимости 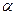 . Чаще всего в статистико-экономических исследованиях используют такие уровни значимости, как
. Чаще всего в статистико-экономических исследованиях используют такие уровни значимости, как 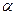 =0,05 и
=0,05 и 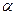 =0,01. Если F> F табл, то выборочная совокупность и связь между признаками являются значительными.
=0,01. Если F> F табл, то выборочная совокупность и связь между признаками являются значительными.
Для парной линейной регрессии при r = R расчетные значения t –критерия Стьюдента определяются по формуле:
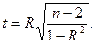
Критерий Стьюдента дает оценку значимости коэффициента корреляции R и существенности связи между признаками.
Рассчитанное по формуле теоретическое значение t –критерия Стьюдента сравнивают с табличным для соответствующего числа степеней свободы и принятого уровня значимости 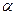 . Табличное значение критерия Стьюдента выбирается из справочных математических таблиц. Если t>tтабл,то линейный коэффициент корреляции считается значимым при характеристике генеральной совокупности.
. Табличное значение критерия Стьюдента выбирается из справочных математических таблиц. Если t>tтабл,то линейный коэффициент корреляции считается значимым при характеристике генеральной совокупности.
Понятие об ошибках выборки.
Ошибка выборки возникает из-за различий в вариации значений изучаемого признака у единиц выборочной и генеральной совокупности. Поскольку при соблюдении требований случайного отбора все единицы генеральной совокупности имеют равные шансы попасть в выборку, состав выборки может значительно изменяться при повторении испытаний. Соответственно будут меняться параметры выборки, и возникать ошибки выборки. Ошибки выборки неизбежны, они вытекают из сути метода. Ошибки выборки не могут быть постоянными при повторении отбора.
Вероятность появления определенной ошибки выборки находят с помощью теорем теории вероятностей. Согласно теореме Чебышева, при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности вероятность того, что разность между выборочной средней и генеральной средней будет сколь угодно мала, близка к единице:
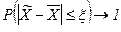 при
при 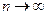 .
.
А. М. Ляпунов доказал, что независимо от характера распределения генеральной совокупности при увеличении объема выборки распределение вероятностей появления того или иного значения выборочной средней приближается к нормальному распределению (центральная предельная теорема). Следовательно, вероятность отклонения выборочной средней от генеральной средней, т.е. вероятность появления заданной предельной ошибки, также подчиняется указанному закону и может быть найдена как функция от t с помощью интеграла вероятностей Лапласа:
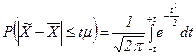 ,
,
где 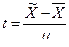 – нормированное отклонение выборочной средней от генеральной средней.
– нормированное отклонение выборочной средней от генеральной средней.
При определении ошибки выборки речь идет о том, чтобы максимально приблизить показатели выборочной совокупности к показателям генеральной совокупности и выявить допустимые граничные отклонения этих показателей.
В процессе выборочного наблюдения возможно решить 2 задачи:
- установить пределы (границы) среднего значения признака в генеральной совокупности: 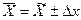 ;
;
- найти пределы (границы) доли альтернативного признака в генеральной совокупности:  .
.
Ошибка репрезентативности, или разница между выборочной и генеральной характеристикой (долей или средней), которая возникает вследствие несплошного наблюдения, в основе которого лежит случайный отбор, рассчитывается как граница вероятной ошибки (предельная ошибка выборки).
В общем виде предельная ошибка выборки определяется (на основе теоремы Ляпунова) как:
 = t
= t 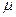 ,
,
где t – коэффициент доверия, зависящий от вероятности, с которой определяется предельная ошибка выборки (значения t при заданной вероятности P определяются по таблице значений, которая рассчитывается по формуле Лапласа).
Например, при P=0,683 t =1,
при P=0,954 t =2,
при P=0,997 t =3.
Вероятность, которая принимается при расчете выборочной характеристики, называется доверительной. В качестве уровня доверительной (гарантированной) вероятности принимается, обычно, 0,954 или 0,997. Тогда граница ошибки определяется величиной, удвоенной или утроенной по отношению к средней ошибке выборки 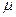 .
.
Средняя ошибка выборки определяется по формулам:
- для повторного случайного отбора
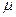 =
= 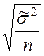 ;
;
– для бесповторного случайного и механического отборов
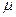 =
= 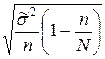 ;
;
где 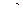 - дисперсия (для типовой выборки - средняя из внутригрупповых дисперсий; для простой случайной и механической выборок – дисперсия выборочной совокупности).
- дисперсия (для типовой выборки - средняя из внутригрупповых дисперсий; для простой случайной и механической выборок – дисперсия выборочной совокупности).
Таким образом, предельная ошибка выборки для средней рассчитывается по формулам:
- для повторного случайного отбора
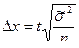 ;
;
– для бесповторного случайного и механического отборов
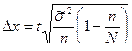 .
.
Предельная ошибка выборки для доли альтернативного признака:
- при повторном отборе
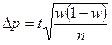 ,
,
- при бесповторном
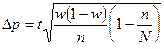 ,
,
где 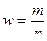 - доля альтернативного признака;
- доля альтернативного признака;
m -численность совокупности по альтернативному признаку;
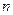 - численность выборочной совокупности.
- численность выборочной совокупности.
Следовательно, при выборочном наблюдении определяется не одно, точное значение обобщающей характеристики генеральной совокупности, а лишь ее доверительный интервал с заданным уровнем вероятности. И это серьезный недостаток выборочного метода статистики.
Вероятности конкретного размера ошибок подсчитать невозможно (нецелесообразно), гораздо важнее знать, что ошибка наблюдений не выйдет за определенные пределы.
Рассмотрим пример. Допустим, в результате выборочного исследования жилищных условий жителей города, осуществленного на основе случайной повторной выборки, получен такой ряд распределения.
Таблиця 9.1
Таблиця 9.3.
Понятие рядов динамики.
Процесс развития и движения социально-экономических явлений во времени в статистике называют динамикой. Для ее отображения строятся ряды динамики.
Ряды динамики – это ряды последовательно расставленных в хронологическом порядке показателей, которые характеризуют развитие явления.
В ряде динамики выделяют 2 основных показателя: уровень ряда (распределения) у (числовые данные показателя ряда динамики) и показатель времени t (соответствует конкретным моментам или периодам, к которым относятся уровни).
Ряды динамики, как правило, представляют в виде таблицы (табл.10.1) или графически (рис.10.1), причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.
Таблица 10.1
Внешнеторговый оборот страны за период 2009-2015 гг.
| Год | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| Млрд. долл. США | 149,9 | 155,6 | 168,3 | 212,0 | 280,6 | 368,9 | 468,4 |
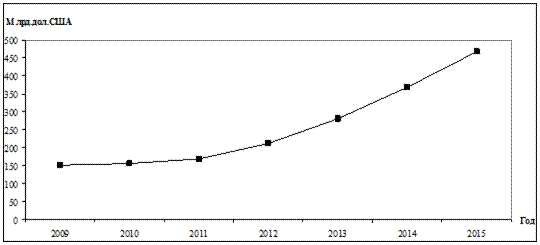
Рис.10.1. Внешнеторговый оборот страны за период 2009-2015 гг.
При статистическом изучении динамики решаются следующие задания:
1. Определение скорости и интенсивности развития явления с помощью изменения уровней ряда и средних величин.
2. Определение основной тенденции ряда динамики (тренда), который позволяет представить изменение уровней ряда за определенный промежуток времени в виде модели.
3. Определение величины колебания уровней ряда вокруг тренда.
4. Сравнение во времени отдельных социально-экономических показателей разных государств.
5. Использование методов анализа динамических рядов для прогнозирования и интерполяции.
Одной из основных проблем построения рядов динамики является сопоставимость уровней этих рядов, которая достигается или в процессе сбора и обработки данных, или путем их пересчета.
Для обеспечения сопоставимости уровней ряда динамики необходимо выполнять следующие требования:
- уровни рядов динамики должны быть сопоставлены во времени, по территориям и объектам с целью избежать влияния фактора цен на экономические показатели;
- уровни рядов динамики должны быть однозначными по экономическому содержанию и иметь одинаковые единицы измерения;
- необходимо придерживаться единой методологии расчета показателей ряда динамики.
В зависимости от способа выражения уровней ряда ряды динамики классифицируют:
- ряды абсолютных величин (например, статистические данные о производстве строительных материалов за определенный период времени);
- ряды относительных величин (например, ряд, который показывает удельный вес городского населения в общем его количестве за несколько лет);
- ряды средних величин (например, данные о средней урожайности сельскохозяйственных культур за несколько лет).
В зависимости от того как отображают уровни ряда состояние явления ряды динамики делят на:
- моментные, которые отображают состояние явления на конкретную дату (например, состояние фермерских хозяйств в области на конец года);
- интервальные, уровни которых характеризуют явление за определенный промежуток времени (например, данные о валовом сборе зерновых культур за 5 лет).
Интервал моментного ряда – это промежуток времени между датами, на которые приведена информация.
Показатели интервального ряда можно суммировать. Такая операция называется укрупнением временных интервалов.
Разновидностью интервальных рядов являются ряды динамики с нарастающими итогами. Они применяются для оценки хода выполнения запланированных показателей и текущего, сравнение результатов деятельности разных хозяйственных субъектов. Каждый уровень такого ряда – это сумма значений анализируемого показателя за все предшествующие периоды его регистрации.
ТЕМА 12. ИНДЕКСЫ.
1. Понятие и классификация индексов.
2. Индивидуальные и общие индексы.
3. Средний арифметический и средний гармонический индексы.
4. Индексы фиксированного и переменного состава и структурных сдвигов.
5. Взаимосвязь индексов.
При построении агрегатного индекса количественного (объемного) показателя соизмерителем выступает качественный показатель, при построении агрегатного индекса качественного показателя соизмерителем является количественный (объемный) показатель.
Например, агрегатный индекс стоимости продукции (объемный показатель) определяется по формуле:
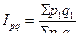 .
.
Этот индекс показывает во сколько раз увеличилась (уменшилась) стоимость продукции отчетного периода в сравнении с базисным.
Разность числителя и знаменателя индекса ( S q1p1- S q0p0 ) показывает абсолютный прирост результативного показателя.
Численное значение индекса стоимости продукции определяется двумя факторами:
- изменением количества (объема) товара;
- изменением цен.
Для того, чтобы оценить изменение стоимости только за счет одного фактора, необходимо устранить влияние другого фактора. Это можно сделать, если зафиксировать в формуле данный фактор неизменным, т.е. на уровне одного и того же периода (т.е. используя индексы Пааше и Ласпейреса).
Если целью анализа является определение экономическго эффекта (прибыль, убуток) от изменения цен в отчетном периоде по сравнению с базисным, то используется индекс Пааше.
Если целью анализа является прогнозирование объема продаж в связи с возможным изменением цен в предстоящем периоде, то используется индекс Ласпейреса.
Численное значение индекса, рассчитанное по формуле Пааше всегда выше, чем рассчитанное по формуле Ласпейреса.
Как правило, для индексов качественных показателей весовой показатель принимается на уровне отчетного периода, для индексов количественных показателей – на уровне базисного периода.
К агрегатным индексам качественных показателей относятся:
- агрегатный индекс цен (Ір);
- агрегатный индекс себестоимости (Іz);
- агрегатный индекс трудоемкости (Іt);
- агрегатный индекс производительности труда (Іw).
Взаимосвязь индексов.
Взаимосвязь экономических индексов позволяет осуществить оценку роли отдельных факторов в изменении исследуемого явления.
Так, произведение индексов количественных и качественных показателей дает индекс объемного.
Например, индекс стоимости продукции равен произведению индексов цены и физического объема реализации:
 ,
,
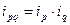 .
.
Используя взаимосвязь индексов можно получить одни индексы на основе других.
Например, если товарооборот по группе товаров увеличился 1,2 раза, а цены снизились в среднем на 10%, то физический объем товарооборота увеличился на 33% (1,2:0,9=1,33). (  .Следовательно,
.Следовательно,  )
)
Т.е. рост товарооборота на 20% произошел за счет увеличения его физического объема на 33% и снижения цен на 10%.
ЛИТЕРАТУРА
Основная литература
1. Герасименко С.С. Статистика: Підручник / С.С. Герасименко. – К.: КНЕУ, 2010.
2. Гусаров В.М. Теория статистики: Учеб. Пособие / В.М. Гусаров. – М.: ЮНИТИ-ДАНА, 2008. -463 с.
3. Ефимова М.Р. Общая теория статистики: Ученик / М.Р. Ефимова. – М.: ИНФРА-М, 2008. – 236 с.
4. Лугінін О.Є. Статистика. Підручник / О.Є. Лугінін. - К.: Центр навчальної літератури, 2010.-580 с.
5. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник / Под ред. А.А. Спирина, О.Э. Башиной. – М.: Финансы и статистика, 2009. – 325 с.
6. Теория статистики: Учебник / Под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 2005. -464 с.
7. УманецьТ.В. Економічна статистика: Навч. посібник / Т.В. Уманець. -К.: Знання, 2009.-429 с.
Дополнительная литература
1. Головач А.В. Статистика. Збірник задач: Навч. посібник / А.В.Головач, А.М. Єріна, О.В. Козирєв та ін. – К.: Вища шк., 2006.
2. Экономическая статистика: Учебник / Под ред. Ю.Н. Иванова - М.: ИНФРА-М, 2008. - 480с.
3. Статистика. Учебник для вузов / Под ред. И.И.Елисеевой .- СПб.: Питер, 2012.-368 с.
4. Акімова О.В. Статистика в малюнках та схемах: Навчальний посібник / О.В. Акімова – К.: Центр учбової літератури, 2007.-168 с.
5. Бек В.Л. Теорія статистики: Навч. посібник / В.Л. Бек - К.: Центр навчальної літератури, 2008.-288 с.
Электронные ресурсы
1. http://www.libertarium.ru/library - библиотека материалов по экономической тематике
2. http://www.ise.openlab.spb.ru - Галерея экономистов
3. http://www.nobel.se/economics/laureates - Лауреаты Нобелевской премии по экономике
4. http://www.minfin.ru - Официальный сайт Министерства финансов
5. http://www. mse.ru - Межбанковская фондовая биржа
6. http://www.budgetrf.ru - Мониторинг экономических показателей
[1]
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ ДНР
ГОУ ВПО «ДОНБАССКАЯ НАЦИОНАЛЬНАЯ АКАДЕМИЯ СТРОИТЕЛЬСТВА И АРХИТЕКТУРЫ»
КАФЕДРА «ЭКОНОМИЧЕСКАЯ ТЕОРИЯ И ИНФОРМАЦИОННО-СТОИМОСТНОЙ ИНЖИНИРИНГ»
УТВЕРЖДАЮ
Зав. кафедрой
"Экономическая теория и информационно-
стоимостной инжиниринг"
___________ / ______________
«____» _______________2016 г.
КОНСПЕКТ ЛЕКЦИЙ
"Теория статистики"
для направления
38.03.02 "Менеджмент"
Макеевка
2016
СОДЕРЖАНИЕ
| Содержательный модуль 1. Теоретические основы статистики…… | 3 |
| Тема 1. Методологические основы статистики………………………….. | 3 |
| Тема 2. Статистическое наблюдение……………………………………... | 10 |
| Тема 3. Сводка, группировка статистических данных………………….. | 17 |
| Тема 4. Представление статистических данных: таблицы, графики, карты………………………………………………………………………..… | 24 |
| Тема 5. Обобщающие статистические показатели………………………. | 32 |
| Содержательный модуль 2. Статистические методы исследования вариации и динамика показателей…………………………………….. | 40 |
| Тема 6. Анализ рядов распределения…………………………………... | 40 |
| Тема 7. Анализ концентрации, дифференциации распределения……. | 50 |
| Тема 8. Статистические методы измерения взаимосвязи……………….. | 60 |
| Содержательный модуль 3. Методы исследования показателей статистического анализа социально - экономических явлений……. | 71 |
| Тема 9. Выборочное наблюдение…………………………………………. | 71 |
| Тема 10 . Анализ интенсивности динамики……………………………… | 84 |
| Тема 11. Анализ тенденций развития…………………………………….. | 89 |
| Тема 12. Индексы…………………………………………………..……... | 95 |
| Литература………………………………………………………………….. | 104 |
МОДУЛЬ 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ СТАТИСТИКИ
ТЕМА 1. МЕТОДОЛОГИЧЕСКИЕ ОСНОВЫ СТАТИСТИКИ.
1. Статистика как наука.
2. Предмет статистики и ее категории.
3. Методология статистики и ее задачи
Статистика как наука.
Статистика предоставляет человечеству разнообразную информацию, осуществляет учет многих явлений и процессов (численность мужского и женского населения, количество земельных угодий, сырья, ресурсов, государственного дохода и т.д.).
Термин «статистика» произошел от латинского слова «статус» (status), который использовался вначале в значении «сумма знаний о государстве». В науку термин «статистика» ввел ученый Готфрид Ахенваль в 1746 году, предложив заменить название курса «Государствоведение», преподававшегося в университетах Германии, на «Статистику», положив начало развитию статистики как науки и учебной дисциплины. Несмотря на это, статистический учет велся намного раньше: проводились переписи населения в Древнем Китае, осуществлялось сравнение военного потенциала государств, велся учет имущества граждан в Древнем Риме и пр. При углублении общественного разделения труда, развития производства увеличивалось количество учитываемых факторов и как следствие количество рассчитываемых показателей.
Статистика как наука развивалась по нескольким направлениям: описательному, математическому и математико-статистическому.
Представители описательной школы (Герман Конринг, Готфрид Ахенваль) своей задачей считали описание достопримечательностей государства: территории, населения, политического устройства.
Представители математического направления или школы «политической арифметики» (Уильям Петти, Джон Граунт) выявляли на основе большого числа наблюдений различные закономерности и взаимосвязи в изучаемых явлениях.
Математико-статистическое направление возникло в начале ХІХ века. Представители этого направления (К. Пирсон, А.Кетле, Р.Фишер, М.Митчел) использовали в статистических исследованиях математические методы.
Особенностью статистики является то, что статистические данные предоставляются в количественной форме, т.е. статистика говорит языком цифр, которые отображают общественную жизнь в ее разнообразии.
На современном этапе под статистикой понимают и направление практической деятельностью, и экономическую науку, и учебную дисциплину по изучению способов сбора, обработки и анализа данных о массовых социально-экономических явлениях и процессах.
Как направление практической деятельности статистика занимается сбором, накоплением, обработкой цифровых данных, которые характеризуют экономику, население, культуру, образование и другие явления в жизни общества.
Также статистикой называют науку, т.е. отрасль знаний, которая изучает массовые явления в жизни общества с их количественной стороны.
Основой для изучения массовых явлений является закон больших чисел, сущность которого состоит в том, что количественные закономерности массовых явлений отчетливо проявляются лишь в достаточно большом их числе. Т.е. каждое единичное явление является случайным (т.е. оно может быть или не быть), но при объединении большого количества таких явлений в общей характеристике их массы случайность тем больше уменьшается, чем больше объединяется единичных явлений (например, урожайность на одном конкретном поле может быть больше или меньше, даже если оно удобрено лучше другого, а урожайность в целом большого количества хорошо удобренных полей будет выше, чем большого количества полей хуже удобренных).
Дата: 2018-12-28, просмотров: 1321.