Двигателя, исполнительного механизма
И силового преобразователя
Передаточная функция двигателя по управляющему воздействию
,
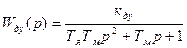где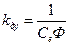 
,
, 
,
.
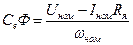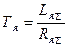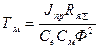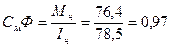Нм/А
Сопротивление Rя определим из номинальных данных двигателя, решая систему уравнений:
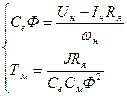
в итоге получим Rя=0,041Ом.
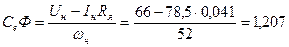Вс/рад
Следовательно,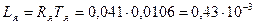 
Гн.
Суммарное сопротивление якорной цепи с учетом щеточного контакта, силового преобразователя и нагрева:
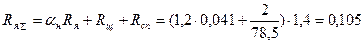Ом.
Приведенный момент инерции
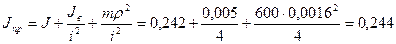кгм2.
Отсюда параметры передаточной функции двигателя по управляющему воздействию
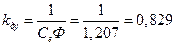рад/В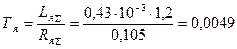с;
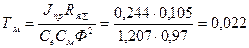с;
с;
.
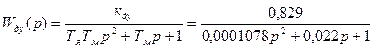Корни знаменателя передаточной функции:
р1=-135,76
р2=-68,32.
Следовательно, передаточную функцию двигателя можно представить двойным апериодическим звеном:
,
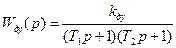где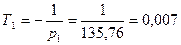 
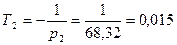с,
с.
Передаточная функция исполнительного механизма:
.
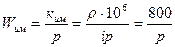Передаточная функция транзисторного силового преобразователя – безынерционное звено с коэффициентом передачи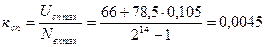 
В/дискр.
Структурная схема аналогового прототипа
Позиционно-следящего электропривода. Расчет
Параметров регуляторов
Структурная схема следящего структурно-минимального электропривода приведена на рис. 4.
Поскольку двигатель описывается двойным апериодическим звеном, то постоянную времени пропорционально-дифференциального регулятора выбираем равной
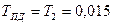с.
Коэффициент передачи пропорционально-диффернциального регулятора и постоянную времени интегрального регулятора определим из областей показателей качества регулирования СМЭПа. При этом будем считать, что изображающая точка, характеризующая качество регулирования, должна находиться в области монотонности для обеспечения одностороннего подхода к заданной координате. Выберем координаты изображающей точки следующим образом:
М(0,1Ти; 0,2Ти),
где абсцисса точки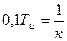 
, а ордината 
.
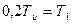Из ординаты точки М определяем постоянную времени интегрального регулятора.
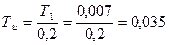с
Из абсциссы точки М определим требуемый коэффициент передачи внутреннего разомкнутого контура.
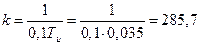
Отсюда коэффициент передачи пропорционально-дифференциального регулятора
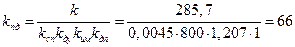
Структурная схема структурно-минимального
Электропривода с учетом квантования по времени.
Дискретные передаточные функции непрерывной части
системы с учетом экстраполятора нулевого порядка,
Цифровых регуляторов и замкнутого электропривода
В целом
Структурная схема цифрового следящего СМЭП с учетом процесса квантования сигналов по времени приведена на рис. 6. Функцию экстраполятора нулевого порядка в структурно-минимальном электроприводе выполняет цифровой силовой преобразователь. При переходе к z-преобразованиям структурная схема СМЭП с учетом дискретных передаточных функций принимает вид, приведенный на рис. 7.
Дискретная передаточная функция первого регулятора, вычисляющего производную как первую обратную разность
,
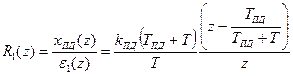где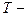 
период дискретизации; 
.
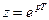При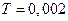 
с
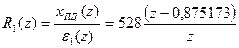
Дискретная передаточная функция второго регулятора, вычисляющего интеграл как полную сумму
.
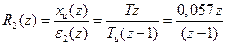Дискретная передаточная функция непрерывной части системы с учетом экстраполятора нулевого порядка
,
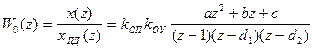где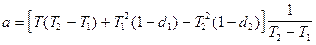 
;
;
;
; 
.
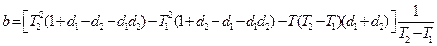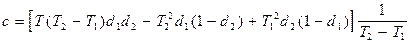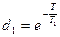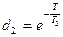Подставляя сюда значения параметров электродвигателя, силового преобразователя и периода дискретизации получим:
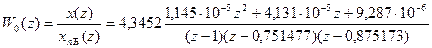
Пропорционально-дифференциальный регулятор предназначен для компенсации наибольшего полюса передаточной функции, поэтому
.
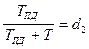С учетом этого дискретная передаточная функция СМЭП
,
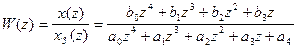где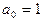 
; 
;
;
; 
;
; 
;
;
.
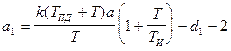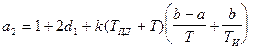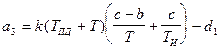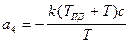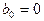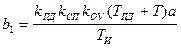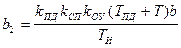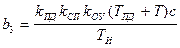Подставляя численные значения всех параметров в итоге получим:
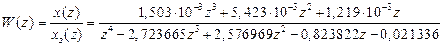
Передаточная функция позволяет исследовать динамические характеристики цифрового следящего СМЭП с учетом процесса квантования по времени.
Дата: 2018-12-28, просмотров: 203.
