Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

При изготовлении КМ конструкционного назначения основной целью наполнения является получение усиленного полимерного мате­риала, т.е. материала с улучшенным комплексом физико-механических свойств. Достигается это как введением волокнистых армирующих наполнителей, так и тонкодисперсных наполнителей, рубленого стек­ловолокна, аэросила и др. При создании КМ со специальными свойст­вами наполнители, как правило, вводятся для того, чтобы придать ма­териалу не механические, а желаемые электрофизические, термиче­ские, сенсорные и другие свойства. При этом частицы наполнителя тем или иным способом распределяются в полимерной матрице.

По характеру распределения компонентов композиты можно раз­делить:

1. на матричные системы;

2. статистические смеси;

3. структурированные композиции.

На рисунке 11 изображены типичные структуры композитов и распределение наполнителя в матрице.

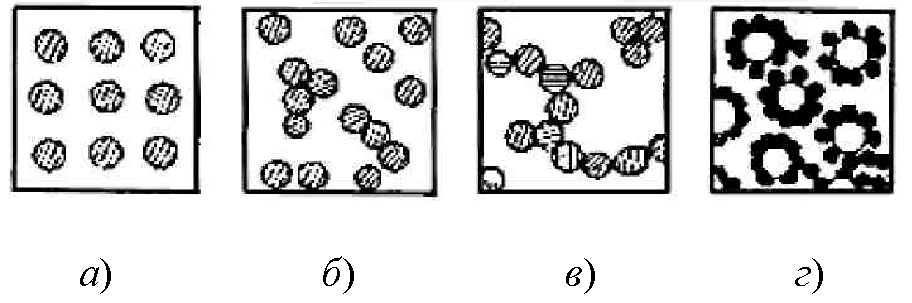
Рис. 11. Структуры композитов и распределение наполнителей в матрице

В матричных (регулярных) системах частицы наполнителя рас­полагаются в узлах регулярной решётки (а). В статистических систе­мах компоненты распределены хаотично и не образуют регулярных структур (б). К структурированным композитам относят системы, в которых компоненты образуют цепочечные, плоские или объёмные структуры (в, г).

Топология гетерогенных систем (композитов)

Под топологией КМ понимается форма частиц дисперсной фазы, их размеры, а также распределение дисперсной фазы по объёму дис­персионной среды. Сюда также входят размер включений, расстояние между ними, координаты центров включений, угол ориентации в про­странстве неизомерных включений (т.е. включений, размер которых в одном либо двух выделенных направлениях намного превышает раз­мер в других направлениях, например волокна, пластины).

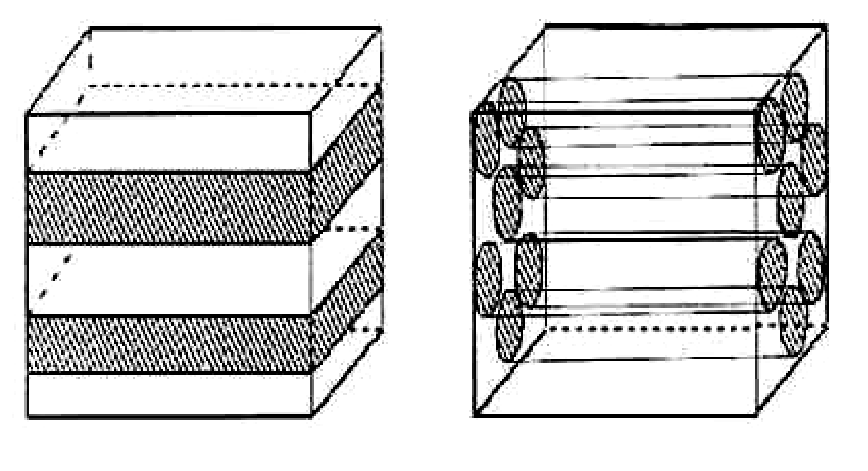
Рис 12- Микрогеометрия укладки наполнителя параллельными слоями (слева), определяется верхней границей Винера; перпендикулярными слоями (справа) - нижней границей Винера

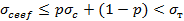КМ на основе одноосно-ориентированных непрерывных волокон или тканей (рис. 12) легко поддаются анализу. В направлении вдоль волокон (в плоскости слоёв ткани) электропроводность КМ (верхняя граница Винера), в перпендикулярном направлении 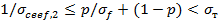(нижняя граница Винера). Здесь  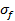и 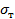т - электропроводность наполнителя и матрицы, р - объёмная доля наполнителя. Эти выражения имеют общий характер, поскольку соответствуют эффективной проводимости двухфазной системы при последовательном и параллельном действии фаз и являются оптималь­ными при условии, что известны лишь объёмные доли каждой фазы. Нетрудно показать, что для слоистых композиционных материалов продольная проводимость 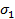всегда выше, чем проводимость 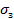в на­правлении, перпендикулярном слоям. Действительно, для пачки слоёв толщиной 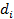и проводимостью  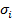продольная проводимость равна 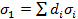а поперечная проводимость 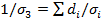. Средняя про­дольная проводимость 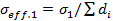. Средняя поперечная проводи­мость 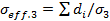. Используя неравенство Коши-Буняковского, по­лучаем, что .

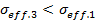Верхняя и нижняя границы Винера определяют область значений электропроводности КМ при данном соотношении параметров матри­цы и наполнителя независимо от формы частиц и способа приготовле­ния КМ. В действительности границы Винера дают слишком грубую оценку проводимости, так как не учитывают топологии композита, контактов между частицами наполнителя и другие факторы, но позво­ляют оценить диапазон изменения проводимости и других транспорт­ных характеристик (например, теплопроводности) для конкретной па­ры компонентов КМ.

Некоторые топологические характеристики ряда часто встречаю­щихся структур композиционных материалов приведены в таблице 5

Таблица 5-Геометрическая структура гетерогенных систем

 

Геометрическая	Характеристика	Характеристика
Характеристика	направленности	размерности
Регулярные структуры
Параллельные слои	Анизотропия сильная	Двумерная
Параллельные волокна	Анизотропия сильная	Одномерная
в матрице
Шаровые включения	Анизотропия слабая	Трёхмерная
в матрице
Взаимопроникающие	Анизотропия слабая	Трёхмерная
Каркасы
Нерегулярные структуры
Хаотически ориентиро-	Изотропия	Трёхмерная
ванные волокна
в матрице
Хаотически ориентиро-	Изотропия	Трёхмерная
ванные контактирую-
щие волокна
Преимущественно ори-	Анизотропия	Трёхмерная
ентированные волокна
в матрице
Случайно расположен­	Изотропия	Трёхмерная
ные шаровые включе­
ния в матрице
Статистическая смесь	Изотропия	Трёхмерная
изомерных полиэдров

 

Вопросы для самоконтроля

1. Типичные структуры композитов

2. Топология композитов