91-100. Исследовать методами дифференциального исчисления функцию 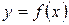 и, используя результаты исследования, построить ее график.
и, используя результаты исследования, построить ее график.
91. 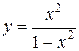 . 96.
. 96.  .
.
92. 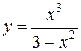 . 97.
. 97. 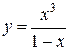 .
.
93. 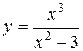 . 98.
. 98. 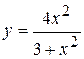 .
.
94.  . 99.
. 99. 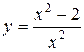 .
.
95.  . 100.
. 100. 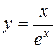 .
.
Пример. 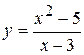 .
.
1. Область определения: 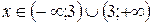 .
.
2. 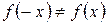 ,
, 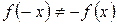 , -следовательно, функция не является четной, нечетной, периодической.
, -следовательно, функция не является четной, нечетной, периодической.
3. Исследуем характер точки разрыва 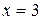 и поведение функции вблизи этой точки:
и поведение функции вблизи этой точки:
 ,
,
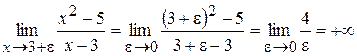 .
.
Таким образом, в точке 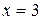 функция терпит разрыв второго рода, а прямая
функция терпит разрыв второго рода, а прямая 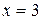 является вертикальной асимптотой.
является вертикальной асимптотой.
4. Определим уравнение наклонной асимптоты:
 , где
, где
 ,
,
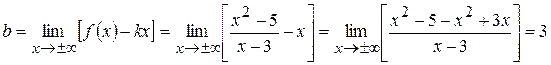 .
.
Итак,
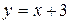 - наклонная асимптота.
- наклонная асимптота.
5. Определим критические точки.
 ,
,
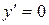 при
при 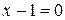 или
или  , то есть при
, то есть при  или
или  , - других критических точек в области определения функции нет. Значения функции в критических точках:
, - других критических точек в области определения функции нет. Значения функции в критических точках:
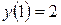 ,
,  .
.
6. Найдем вторую производную:
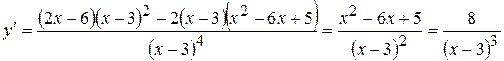 .
.
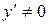 , следовательно, точек перегиба нет.
, следовательно, точек перегиба нет.
7. Внесем все полученные данные в таблицу, определим поведение функции на различных участках и построим график.
| x | 
| 1 | 
| 3 | 
| 5 | 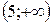
|
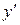
| + | 0 | - | - | 0 | + | |
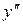
| - | - | - | + | + | + | |
   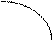 y y
| 2 max | 10 min |
Положительные значения первой производной соответствуют промежуткам возрастания, отрицательные – промежуткам убывания. Положительные значения второй производной соответствуют промежуткам вогнутости функции, отрицательные – промежуткам выпуклости. Точка, в которой возрастание функции сменяется убыванием, является точкой максимума, а точка, в которой убывание функции сменяется возрастанием – точкой минимума.

Неопределённый и определённый интегралы
101-110. Найти неопределённые интегралы.
101. а). 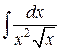 ; б).
; б). 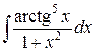 ; в).
; в). 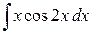 .
.
102. а).  ; б)
; б) 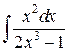 ; в).
; в). 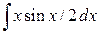 .
.
103. а). 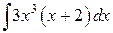 ; б)
; б) 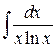 ; в).
; в). 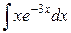 .
.
104. а).  ; б)
; б) 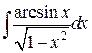 ; в).
; в). 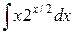 .
.
105. а). 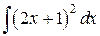 ; б)
; б) 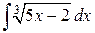 ; в).
; в). 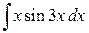 .
.
106. а)  ; б)
; б) 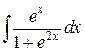 ; в)
; в)  .
.
107. а)  ; б)
; б) 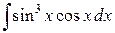 ; в)
; в)  .
.
108. а) 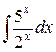 ; б)
; б) 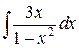 ; в)
; в)  .
.
109. а) 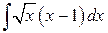 ; б)
; б) 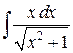 ; в)
; в) 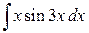 .
.
110. а)  ; б)
; б) 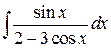 ; в)
; в) 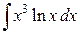 .
.
Пример. Найти неопределённые интегралы.
а) 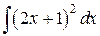 ; б)
; б) 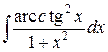 ; в)
; в) 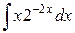 .
.
а) Данный интеграл не является табличным. Поэтому предварительно сделаем элементарные математические преобразования, в данном случае воспользовавшись формулой сокращенного умножения, а потом таблицей интегралов основных элементарных функций, получим:
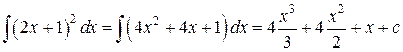
б) пусть требуется найти интеграл вида 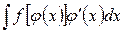 , где подынтегральная функция непрерывна. Сделаем замену
, где подынтегральная функция непрерывна. Сделаем замену 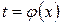 , тогда
, тогда 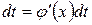 . Получим
. Получим 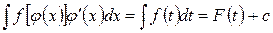 . В найденном интеграле перейдем к прежней переменной
. В найденном интеграле перейдем к прежней переменной 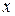 , воспользовавшись равенством
, воспользовавшись равенством  .
.
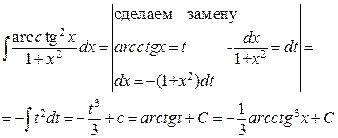 .
.
в) 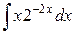 . Имеем интеграл вида
. Имеем интеграл вида 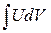 . Применим формулу интегрирования по частям
. Применим формулу интегрирования по частям 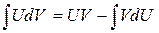 :
:
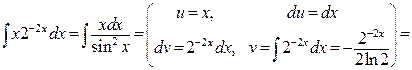
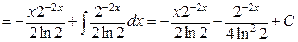 .
.
1 1 1-1 2 0. Вычислить определенные интегралы
111. а) 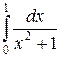 ; б)
; б) 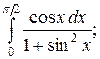 в)
в) 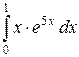 .
.
112. а) 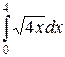 ; б)
; б)  ; в)
; в) 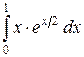 .
.
113. а) 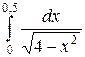 ; б)
; б) 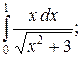 в)
в) 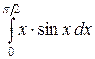 .
.
114. а) 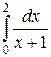 ; б)
; б) 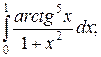 в)
в) 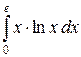 .
.
115. а) 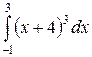 ; б)
; б)  в)
в) 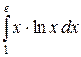 .
.
116. а)  ; б)
; б) 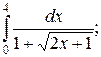 в)
в) 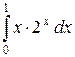 .
.
117. а) 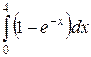 ; б)
; б)  ; в)
; в) 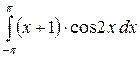 .
.
118. а)  ; б)
; б) 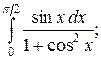 в)
в) 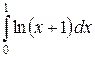 .
.
119. а)  ; б)
; б) 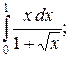 в)
в) 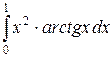 .
.
120. а) 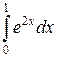 ; б)
; б) 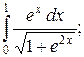 в)
в) 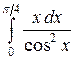 .
.
Пример.
а)  . Применяя формулу Ньютона-Лейбница, вычислим этот интеграл:
. Применяя формулу Ньютона-Лейбница, вычислим этот интеграл:

б) 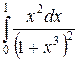 . Вычислим этот интеграл, используя метод замены переменной:
. Вычислим этот интеграл, используя метод замены переменной:

в) 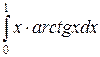 . Применяя формулу интегрирования по частям получим:
. Применяя формулу интегрирования по частям получим:
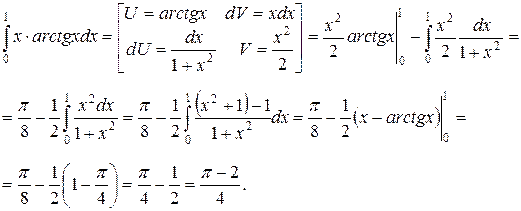
121.-130. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
121. 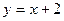 ,
,  . 12 6.
. 12 6. 
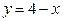
122 . 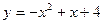 ,
, 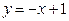 . 12 7.
. 12 7. 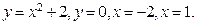
123. 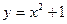 ,
, 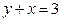 . 12 8.
. 12 8. 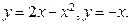
124. 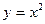 ,
, 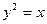 . 12 9.
. 12 9. 
125. 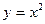 ,
,  . 1 3 0.
. 1 3 0. 
Пример.
а) Вычислить площадь фигуры, ограниченной параболой 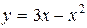 и прямой
и прямой  .
.
Находим точки пересечения данных кривых и строим искомую фигуру
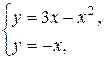

Площадь фигуры, ограниченной снизу кривой 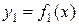 , сверху – кривой
, сверху – кривой  , вычисляет интеграл
, вычисляет интеграл 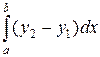 , где
, где  и
и 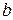 - абсциссы точек пересечения этих кривых, причем
- абсциссы точек пересечения этих кривых, причем 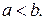
Следовательно, имеем
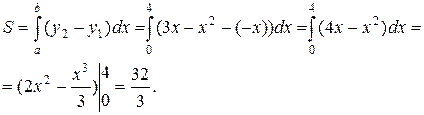
Дифференциальные уравнения.
131 – 140. Найти общее решение дифференциального уравнения.
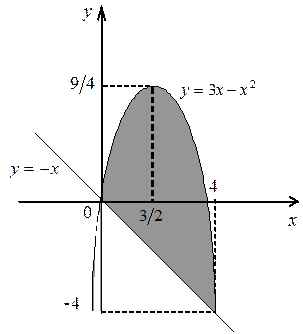
131. а). 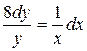 ; б).
; б). 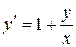 ; в).
; в).  .
.
132. а). 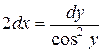 ; б).
; б). 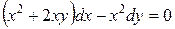 ; в).
; в). 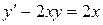 .
.
133. а).  ; б).
; б).  ; в).
; в). 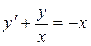 .
.
134. а). 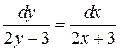 ; б).
; б). 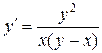 ; в).
; в). 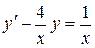 .
.
135. а).  ; б).
; б). 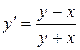 ; в).
; в). 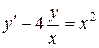 .
.
136. а).  ; б).
; б).  ; в).
; в). 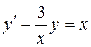 .
.
137. а).  ; б).
; б).  ; в).
; в). 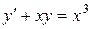 .
.
138. а).  ; б).
; б). 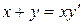 ; в).
; в). 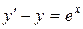 .
.
139. а). 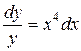 ; б).
; б). 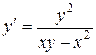 ; в).
; в). 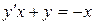 .
.
140. а). 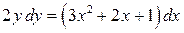 ; б).
; б).  ; в).
; в).  .
.
Пример.
а) 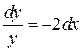 .
.
Данное уравнение является уравнением с разделенными переменными. Проинтегрируем обе его части:
 , получим:
, получим:  .
.
б).  .
.
Для решения данного уравнения используем тот факт, что 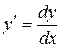 . Так как переменные в данном случае разделить нельзя, то выразим
. Так как переменные в данном случае разделить нельзя, то выразим 
 , отсюда по правилу пропорции получаем:
, отсюда по правилу пропорции получаем:
 , или
, или  .
.
В данном случае 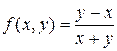 ;
; 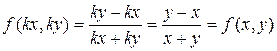 .
.
Следовательно, данное уравнение – однородное. Делаем замену переменной
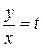 ,
,  ,
, 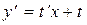 . После замены получим:
. После замены получим:
 ,
,  ,
,  .
.
Получили уравнение с разделяющимися переменными. Разделяя переменные, получим:  ,
,  .
.
Интегрируя, находим общее решение
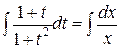 ,
, 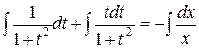 ,
,
 .
.
Возвращаясь к старой переменной, получаем общий интеграл
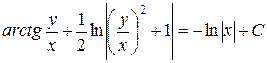 .
.
в). 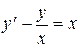 .
.
Данное уравнение линейное. Ищем решение в виде 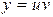 ,
,  .
.
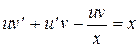 ,
, 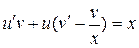 .
.
Решаем уравнение. 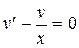 ,
, 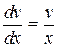 ,
, 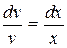 ,
,  ,
,  .
.
Подставляя полученное значение 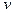 в уравнение, имеем:
в уравнение, имеем:
 ,
,  ,
, 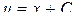 .
.
Общее решение 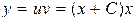 или
или 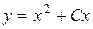 .
.
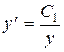 ,
,  ,
, 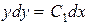 ,
, 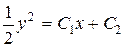 .
.
141–150. Найти общее решение дифференциального уравнения:
141. а). 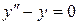 ; б).
; б).  ; в).
; в). 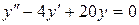 .
.
142. а). 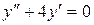 ; б).
; б). 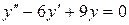 ; в).
; в). 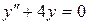 .
.
143. а).  ; б).
; б). 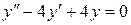 ; в).
; в). 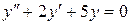 .
.
144. а). 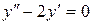 ; б).
; б). 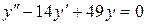 ; в).
; в). 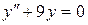 .
.
145. а). 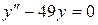 ; б).
; б). 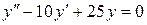 ; в).
; в).  .
.
146. а).  ; б).
; б).  ; в).
; в).  .
.
147. а).  ; б).
; б). 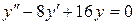 ; в).
; в). 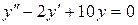 .
.
148. а). 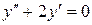 ; б).
; б). 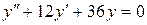 ; в).
; в). 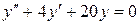 .
.
149. а). 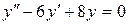 ; б).
; б).  ; в).
; в). 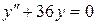 .
.
150. а). 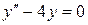 ; б).
; б). 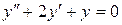 ; в).
; в).  .
.
Пример. а). 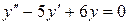 .
.
Составим соответствующее характеристическое уравнение:
 ,
,
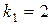 ,
, 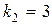 .
.
Так как корни характеристического уравнения 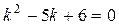 действительные, различные, следовательно, общее решение однородного уравнения имеет вид
действительные, различные, следовательно, общее решение однородного уравнения имеет вид 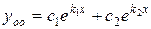 , то есть имеем
, то есть имеем
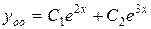 .
.
б).  .
.
Составим соответствующее характеристическое уравнение:
 ,
,
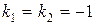 .
.
Так как корни характеристического уравнения  действительные, одинаковые, следовательно, общее решение однородного уравнения имеет вид
действительные, одинаковые, следовательно, общее решение однородного уравнения имеет вид  , то есть имеем
, то есть имеем
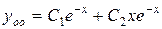 .
.
в). 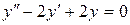 .
.
Составим соответствующее характеристическое уравнение:
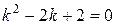 . Решим его при помощи вычисления дискриминанта:
. Решим его при помощи вычисления дискриминанта:
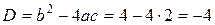 . Так как в данном случае
. Так как в данном случае 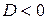 , то для вычисления квадратного корня
, то для вычисления квадратного корня 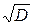 используем равенство
используем равенство 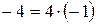 . Так как
. Так как 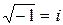 (комплексная единица), то в данном случае
(комплексная единица), то в данном случае 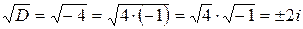 . Таким образом, имеем в данном случае комплексные корни:
. Таким образом, имеем в данном случае комплексные корни:
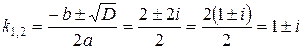 .
.
Так как корни характеристического уравнения 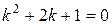 комплексно-сопряженные, следовательно, общее решение однородного уравнения имеет вид
комплексно-сопряженные, следовательно, общее решение однородного уравнения имеет вид  , где
, где 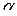 и
и  - соответственно действительная и мнимая части комплексных корней. В данном случае
- соответственно действительная и мнимая части комплексных корней. В данном случае 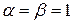 . Таким образом, общее решение исходного уравнения имеет вид:
. Таким образом, общее решение исходного уравнения имеет вид:
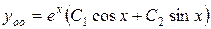 .
.
Дата: 2018-11-18, просмотров: 606.