1. Дайте определения дифференциального уравнения первого порядка и его общего и частного решения (интеграла). Сформулируйте задачу Коши для дифференциального уравнения первого порядка и укажите ее геометрический смысл.

2. Дайте геометрическое истолкование дифференциального уравнения первого порядка, выясните геометрический смысл общего и частного решений.

3. Сформулируйте теорему о существовании и единственности решения дифференциального уравнения первого порядка. Найдите общее решение уравнения 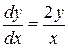 и укажите, где условия этой теоремы не выполняются.

4. Дайте определение дифференциального уравнения с разделяющимися переменными. Изложите метод нахождения его общего решения. Приведите примеры.

5. Дайте определение однородного дифференциального уравнения первого порядка. Изложите метод нахождения его общего решения. Приведите пример.

6. Дайте определение линейного дифференциального уравнения первого порядка. Изложите метод нахождения его общего решения. Приведите пример.

7. Дайте определение уравнения Бернулли. Изложите метод нахождения его общего решения. Приведите пример.

8. Дайте определение линейного дифференциального уравнения n-го порядка (однородного и неоднородного).

9. Дайте определение линейно зависимых и линейно независимых функций и приведите примеры. Сформулируйте обратную теорему для линейно независимых решений (интегралов) однородного линейного дифференциального уравнения.

10. Приведите теорему об общем решении линейного однородного дифференциального уравнения второго порядка.

11. Изложите метод нахождения общего решения линейного однородного дифференциального уравнения второго порядка, если извест­но одно его частное решение. Приведите пример.

12. Приведите формулу для общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае действительных различных корней характеристического уравнения. Приведите пример.

13. Приведите формулу общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае действительных равных корней характеристического уравнения. Приведите пример.

14. Приведите формулу общего решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами в случае комплексных корней характеристического уравнения. Приведите пример.

15. Приведите теорему об общем решении линейного неоднородного дифференциального уравнения второго порядка.

16. Изложите правило нахождения частного решения линейного дифференциального уравнения второго порядка с постоянными коэффициентами и правой частью вида e ^axP_n(x), где Р_n(х) — многочлен степени n≥0.

17. Изложите правило для нахождения частного решения линейного дифференциального уравнения второго порядка с постоянными коэффициентами и правой частью вида e ^ax(A cos βx+B sin βx).

Литература

1. Ильин В.А., Позняк Э.Г.. Аналитическая геометрия.— М.: Наука, 1981.

2. Ефимов Н.В. Краткий курс аналитической геометрии. — М.: Наука, 1967.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.— М.: Высшая школа, 1967-1971. Ч. I, II, III.

4. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов.— М.: Наука, 1970—1985, т. 1, 2.

5. Шкіль М.І., Колесник Т.В., Котлова В.М.. Вища математика.– К.: Либідь, 1994. Т. 1-3.

6. Мышкис А.Д. Лекции по высшей математике — М.: Наука, 1967.

7. Привалов И.И. Аналитическая геометрия.— М., 1956.

8. Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах.— М.: Высшая школа, 1985.

9. Каплан И.А. Практические занятия по высшей математике. – Харьков, 1967.

10. Шестаков А.А., Малышева И.А., Полозков Д.П. Курс высшей математики.— М.: Высшая школа, 1987.

11. Бермант А.Ф., Абрамович И.Г. Краткий курс математического анализа.— М.: Наука, 1973.

12. Мантуров О.В., Матвеев Н.М. Курс высшей математики.— М.: Высшая школа, 1986.

13. Самойленко А.М., Перестюк М.О., Парасюк І.О. Диференціальні рівняння.— К.: Либідь, 1994.

14. Запорожец Г.И. Руководство к решению задач по математическому анализу.— М.: Высшая школа, 1966.

15. Гмурман В.Е. Теория вероятностей и математическая статистика.— М.: Высшая школа, 1972.

16. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.— М.: Высшая школа, 1975.

17. Гурский Е.И. Теория вероятностей с элементами математической статистики. – М.: Высшая школа, 1971.

18. Вентцель Е.С., Овчаров Л.А. Теория вероятностей. Задачи и упражнения.— М.: Наука, 1969.

19. Овчинников П.Ф., Яремчук Ф.П., Михайленко В.М. Высшая математика. — К.: Вища школа, 1987.

20. Высшая математика. Сборник задач / под ред. Овчинникова П.Ф.. — К.: Вища школа, 1991.

21. Герасимчук В.С., Васильченко Г.С., Кравцов В.И. Курс классической математики в примерах и задачах. Ч.1, Донецк. Норд-компьютер, 2002, 528с.

22. Герасимчук В.С., Васильченко Г.С., Кравцов В.И. Курс классической математики в примерах и задачах. Ч.2, Донецк. Норд-компьютер, 2004, 458с.