1-10. Даны координаты вершин треугольника  . Найти: 1) Длины сторон треугольника; 2) Внутренний угол при вершине A треугольника; 3) Уравнение прямой BC; 4) Уравнение высоты, опущенной из вершины A; 5) Уравнение прямой, проходящей через вершину A, параллельно стороне BC.
. Найти: 1) Длины сторон треугольника; 2) Внутренний угол при вершине A треугольника; 3) Уравнение прямой BC; 4) Уравнение высоты, опущенной из вершины A; 5) Уравнение прямой, проходящей через вершину A, параллельно стороне BC.
1. 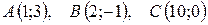 .
.
2. 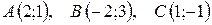 .
.
3.  .
.
4.  .
.
5. 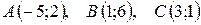 .
.
6.  .
.
7. 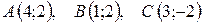 .
.
8. 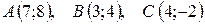 .
.
9. 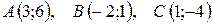 .
.
10. 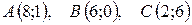 .
.
Пример. 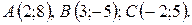
1) Найдем сначала координаты векторов 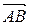 ,
,  и
и 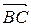 . Для этого из координат конца вектора вычитаем координаты его начала:
. Для этого из координат конца вектора вычитаем координаты его начала:
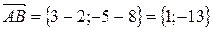 .
.
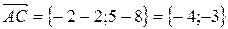 .
.
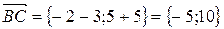 .
.
Модуль вектора (равный расстоянию между точками A и B, A и C, B и C) представляет собой корень из суммы квадратов координат соответствующего вектора:
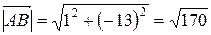 .
.
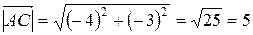 .
.
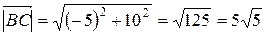 .
.
2) Внутренний угол при вершине A треугольника найдем как угол между сторонами AB и AC треугольника. Этот угол равен углу между векторами 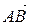 и
и 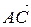 и находится по формуле:
и находится по формуле:
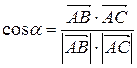 .
.
Тогда 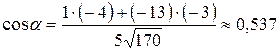 ;
; 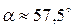 .
.
3) Уравнение прямой BC запишем используя уравнение прямой, проходящей через две точки с координатами 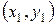 и
и 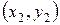 :
:
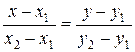 .
.
Подставляя значения координат точек B и C, получим
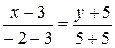 .
.
После приведения подобных получим уравнение прямой BC:
 .
.
4) Высота, опущенная из вершины 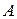 , перпендикулярна стороне
, перпендикулярна стороне 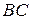 . Следовательно скалярное произведение вектора, лежащего на высоте (будем обозначать его
. Следовательно скалярное произведение вектора, лежащего на высоте (будем обозначать его 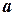 ) и вектора
) и вектора 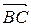 равно нулю. Вектор
равно нулю. Вектор 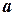 имеет координаты
имеет координаты  , где x и y – координаты произвольной точки, лежащей на высоте. Запишем скалярное произведение
, где x и y – координаты произвольной точки, лежащей на высоте. Запишем скалярное произведение 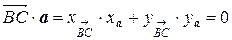 :
:
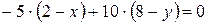 .
.
После раскрытия скобок и приведения подобных получим
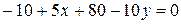 ;
;
 .
.
Это и есть искомое уравнение высоты.
5) Вектор 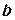 , параллельный стороне
, параллельный стороне 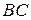 , имеет координаты
, имеет координаты  , где x и y – координаты произвольной точки этого вектора. Из условия параллельности векторов
, где x и y – координаты произвольной точки этого вектора. Из условия параллельности векторов 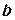 и
и 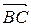 следует
следует  . Подставляя в это соотношение координаты соответствующих векторов и приводя подобные получим
. Подставляя в это соотношение координаты соответствующих векторов и приводя подобные получим
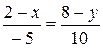 ;
; 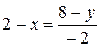 ;
;
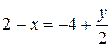 ;
; 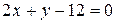 .
.
11-20. Даны координаты вершин пирамиды A1 A2 A3 A4. Найти: 1) длину ребра A1 A2; 2) угол между ребрами A1 A2 и A1 A4; 3) площадь грани A1 A2 A3; 4) объем пирамиды; 5) уравнение плоскости A1 A2 A3; 6) уравнения прямой A1 A4; 7) Угол между ребром A1 A4 и гранью A1 A2 A3; 8) уравнение высоты, опущенной из вершины A4 на плоскость A1 A2 A3.
11. 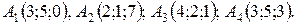
12. 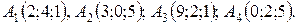
13. 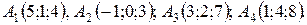
14. 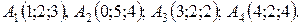
15. 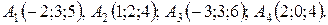
16. 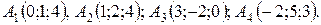
17. 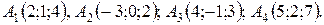
18. 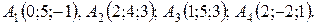
19. 
20. 
Пример. 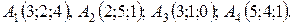
Если точка 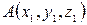 - начало вектора, а точка
- начало вектора, а точка  - его конец, то координаты вектора находятся по формулам
- его конец, то координаты вектора находятся по формулам

1) Найдем сначала координаты вектора 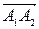 :
:
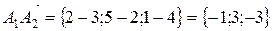 .
.
Модуль вектора (равный расстоянию между точками A1 и A2) представляет собой корень из суммы квадратов координат вектора:
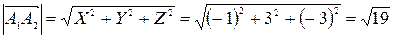 .
.
2) Угол между ребрами A1 A2 и A1 A4 равен углу между соответствующими векторами и находится по формуле:
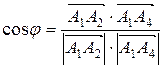 , где
, где 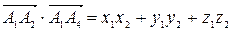 - скалярное произведение векторов, записанное в координатной форме.
- скалярное произведение векторов, записанное в координатной форме.
Координаты вектора 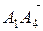 равны:
равны:
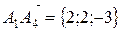 ,
, 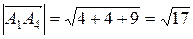 .
.
Тогда 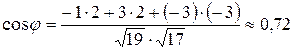 ;
; 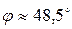 .
.
3) Уравнение плоскости, проходящей через три заданные точки 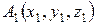 ,
, 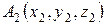 ,
, 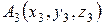 , имеет вид:
, имеет вид:
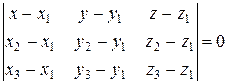 .
.
Подставляя значения координат, вычисляем определитель:
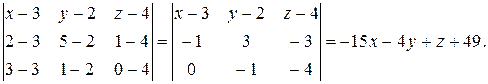
Итак, искомое уравнение плоскости имеет вид
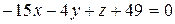 или
или 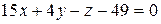 .
.
4) Уравнения прямой, проходящей через точки 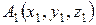 и
и 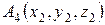 , имеет вид
, имеет вид
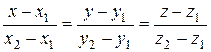 .
.
Таким образом, получаем искомые уравнения:
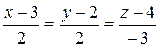 .
.
5) Если даны плоскость 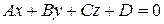 с нормальным вектором
с нормальным вектором 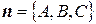 и прямая
и прямая 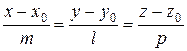 с направляющим вектором
с направляющим вектором 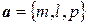 , то угол между прямой и плоскостью определяется по формуле
, то угол между прямой и плоскостью определяется по формуле
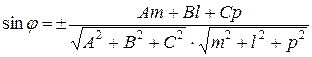 .
.
Так как 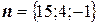 , а
, а  , то
, то
 ,
, 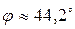 .
.
6) Площадь треугольника, построенного на двух векторах, равна половине модуля векторного произведения этих векторов:
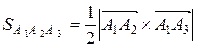 , где
, где  - векторное произведение векторов.
- векторное произведение векторов. 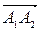 и
и  .
.
Так как
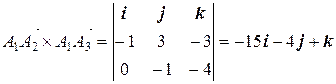 ,
,
то
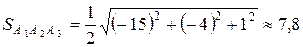 (кв. ед.).
(кв. ед.).
7) Объем пирамиды, построенной на трех векторах, равен одной шестой модуля смешанного произведения этих векторов:
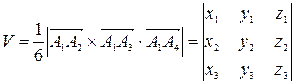 .
.
Следовательно,
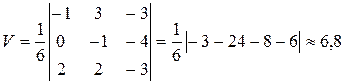 (куб. ед.)
(куб. ед.)
8) Так как в качестве направляющего вектора прямой, проходящей через заданную точку D перпендикулярно плоскости ABC, можно выбрать вектор нормали n к плоскости, то канонические уравнения искомой прямой запишется в виде
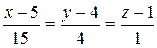 .
.
Пример.2. Из точки P(2;3;-5) на координатные плоскости опущены перпендикуляры. Найти уравнение плоскости, проходящей через их основания.
Основаниями перпендикуляров, опущенных из точки P(2;3;-5) на координатные плоскости, служат точки P1(2;3;0), P2(2;0;-5) и P3(0;3;-5). требуется составить уравнение плоскости, проходящей через три заданные точки.
Чтобы найти нормальный вектор плоскости, рассмотрим два вектора 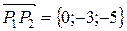 и
и  . Они лежат в искомой плоскости, значит,
. Они лежат в искомой плоскости, значит, 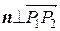 и
и  . Следовательно,
. Следовательно,
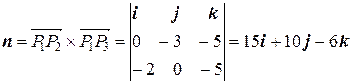 ,
,
Уравнение искомой плоскости, проходящей через точку M1(x1, y1, z1) перпендикулярно вектору 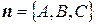 , имеет вид
, имеет вид 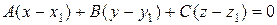 :
:
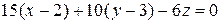 ;
;
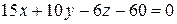 .
.
в) Составить канонические уравнения прямой
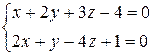
Чтобы найти какую – либо точку, принадлежащую прямой, зафиксируем одну переменную, например z, положив z = 0, и решим полученную систему двух уравнений с двумя неизвестными
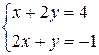
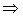
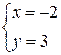
Таким образом, одна из точек, принадлежащих прямой, имеет координаты 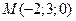 .
.
Теперь найдем направляющий вектор прямой. Так как  и
и 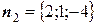 , то
, то
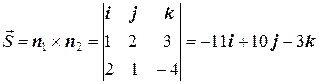 .
.
Канонические уравнения прямой запишутся в виде:
 .
.
Элементы линейной алгебры
21-30. Решить системы линейных уравнений методом Гаусса, Крамера.
21. 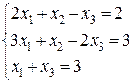 22.
22. 
23. 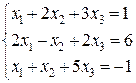 24.
24. 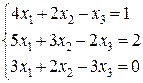
25. 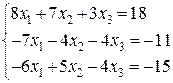 26.
26. 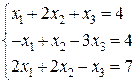
27. 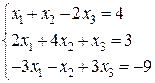 28.
28. 
29. 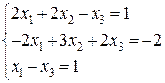 30.
30. 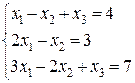
Пример. Решить систему линейных уравнений методом Гаусса и Крамера:

Метод Гаусса.
1. Составляем расширенную матрицу системы и приводим ее к ступенчатому виду, проводя преобразования над строками, позволяющие получить эквивалентную систему (перестановка строк, умножение элементов строк на любое отличное от нуля число, прибавление или вычитание соответствующих элементов строк):
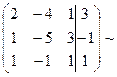
2. Выделяем лидеров строк. Лидер строки - первый ненулевой элемент строки.
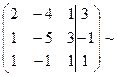
3. При необходимости меняем строки в расширенной матрице системы так, чтобы лидер в строке с наименьшим номером был равен 1. (Перестановка строк в расширенной матрице соответствует перестановке уравнений в системе, а, следовательно, при перестановке строк в матрице мы получим эквивалентную систему). Переставим первое и третье уравнение системы.
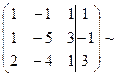
4. Обнуляем лидеров строк, стоящих в строках с большим номером, воспользовавшись элементарными математическими преобразованиями –умножением строки на число, сложение и вычитание строк. Для этого умножим первую строку на (-1) и складываем со второй строкой, затем необходимо первую строку умножить на (-2) и сложить с третьей строкой.
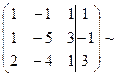
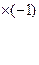
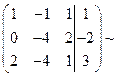
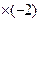
5. После обнуления, снова выделяем лидеров строк.
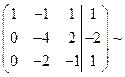
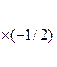
6. Снова обнуляем лидеров строк стоящих в строках с большим номером.
Умножим вторую строку на (-1/2) и сложим с третьей строкой

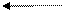
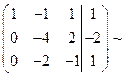
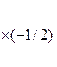
7. Привели матрицу к ступенчатому виду.
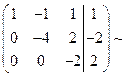
8. Восстанавливаем по приведенной матрице систему. При этом напомним, что третий столбец соответствует коэффициентам, стоящим при неизвестном  , второй - при
, второй - при 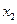 и первый -
и первый - 
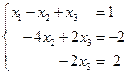
9. Решаем полученную систему и находим неизвестные.
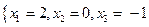
Метод Крамера.
1. Составляем определитель матрицы системы, который составляют из коэффициентов системы уравнений. Для этого выписываем коэффициенты: первое уравнение системы имеет при переменной 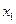 коэффициент 2, при
коэффициент 2, при 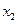 - коэффициент – (-4), при
- коэффициент – (-4), при  - коэффициент 1.
- коэффициент 1.
Записываем все эти коэффициенты в первую строку определителя основной матрицы, коэффициенты второго уравнения во вторую строку и третью соответственно.
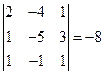 .
.
2. Теперь найдем: ∆ 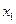 . Для этого первый столбец заменяем столбцом свободных членов.
. Для этого первый столбец заменяем столбцом свободных членов.
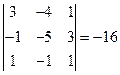 .
.
3. Теперь найдем: ∆ 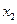 . Для этого второй столбец заменяем столбцом свободных членов.
. Для этого второй столбец заменяем столбцом свободных членов.
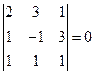 .
.
4. Аналогично находим ∆  . Для этого третий столбец заменяем столбцом свободных членов.
. Для этого третий столбец заменяем столбцом свободных членов.
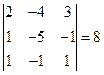 .
.
5. Пользуемся формулами для нахождения неизвестных переменных
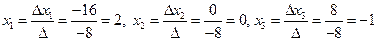
Дата: 2018-11-18, просмотров: 393.