1. Сформулируйте определение производной. Каков ее механический и геометрический смысл?

2. Какой класс функции шире: непрерывных в точке или дифференцируемых в той же точке? Приведите примеры.

3. Приведите формулы производных суммы, произведения, частного двух функций. Приведите примеры.

4. Приведите формулу дифференцирования сложной функции. Приведите примеры.

5. Приведите формулу производной произведения постоянной на функцию.

6. Сформулируйте теорему о производной обратной функции. Приведите формулы дифференцирования обратных тригонометрических функций.

7. Сформулируйте определение дифференциала функции.

8. Для каких точек графика функции ее дифференциал больше приращения? Для каких точек он меньше приращения?

9. Для каких функций дифференциал тождественно равен приращению?

10. В чем заключается свойство инвариантности формы дифференциала функции?

11. Сформулируйте определения производной и дифференциала высших порядков.

12. Каков механический смысл второй производной?

Тема ІV. Возрастание и убывание функций. Экстремумы.

1. Сформулируйте определения возрастающей и убывающей на отрезке функции. Приведите достаточный признак возрастающей функции. Покажите, что функции 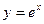y=e^x и y = x + cos x возрастают в любом промежутке.

2. Сформулируйте два правила для отыскания экстремумов функции.

3. Приведите пример, показывающий, что обращение в некоторой точке производной в нуль не является достаточным условием наличия в этой точке экстремума функции.

4. Как найти наибольшее и наименьшее значения функции, дифференцируемой на отрезке? Всегда ли они существуют?

Тема VI. Построение графиков функций.

1. Сформулируйте определения выпуклости и вогнутости линии, точки перегиба. Как находятся интервалы выпуклости и вогнутости и точки перегиба линии, заданной уравнением y=f(x)? Приведите примеры.

2. Сформулируйте определение асимптоты линии. Как находятся вертикальные и наклонные асимптоты линии, заданной уравнением y=f(x)? Приведите примеры.

3. Изложите схему общего исследования функции и построения ее графика.

Тема VII. Неопределенный интеграл.

1. Дайте определение первообразной функции.

2. Укажите геометрический смысл совокупности первообразных функций. Что называется неопределенным интегралом?

3. Напишите таблицу основных интегралов.

4. Приведите простейшие свойства неопределенного интеграла.

5. Найдите 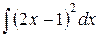 двумя способами: а) непосредственно как интеграл от степенной функции со сложным аргументом; б) раскрыв скобки и проинтегрировав полученную сумму. Покажите, что полученные результаты не противоречат друг другу.

6. Приведите формулу замены переменной в неопределенном интеграле.

7. Приведите формулу интегрирования по частям для неопределенного интеграла. Укажите типы интегралов, вычисление которых целесообразно производить с помощью метода интегрирования по частям.