Раздел Функция.
31-40. Задана функция.
а) найдите область определения и множество значений функции;
б) исследуйте функцию на четность и нечетность.
31.  . 36.
. 36. 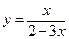 .
.
32. 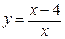 . 37.
. 37. 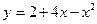 .
.
33. 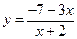 . 38.
. 38. 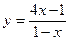 .
.
34. 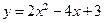 . 39.
. 39. 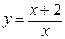 .
.
35. 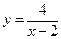 . 40.
. 40. 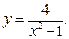
Пример. 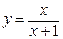 .
.
а) Найдем сначала область определения данной функции. Числитель данной дроби не содержит никаких особенностей, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки: 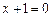 ,
, 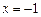 . Данное значение не входит в область определения функции. Действительно, подставьте
. Данное значение не входит в область определения функции. Действительно, подставьте 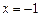 в функцию и вы увидите, что знаменатель обращается в ноль, а на ноль, как известно, делить нельзя. Таким образом, областью определения данной функции, обозначаемая
в функцию и вы увидите, что знаменатель обращается в ноль, а на ноль, как известно, делить нельзя. Таким образом, областью определения данной функции, обозначаемая 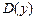 , будет
, будет 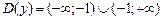 .
.
Теперь найдем множество значений данной функции. Как нетрудно убедиться, исходную функцию можно переписать в виде: 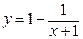 , график которой можно получить из графика функции
, график которой можно получить из графика функции 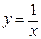 следующими преобразованиями: сдвигом на 1 единицу влево, симметричным отображением относительно Ox и сдвигом на 1 единичный отрезок вверх по оси Oy. Таким образом, областью значений данной функции будет
следующими преобразованиями: сдвигом на 1 единицу влево, симметричным отображением относительно Ox и сдвигом на 1 единичный отрезок вверх по оси Oy. Таким образом, областью значений данной функции будет  .
.
б)Исследуем функцию на четность и нечетность. Найдем 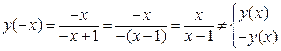
Таким образом, функция не является ни четной, ни нечетной и, значит, данная функция является функцией общего вида.
41-50. Найти пределы функций, не пользуясь правилом Лопиталя.
41. а) 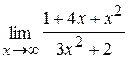 ; б)
; б) 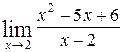 .
.
42. а) 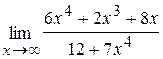 ; б)
; б) 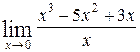 .
.
43. а) 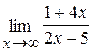 ; б)
; б) 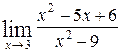 .
.
44. а) 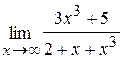 ; б)
; б) 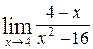 .
.
45. а) 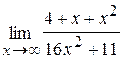 ; б)
; б) 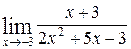 .
.
46. а) 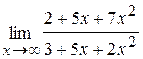 ; б)
; б) 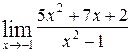 .
.
47. а) 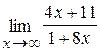 ; б)
; б) 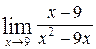 .
.
48. а) 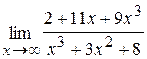 ; б)
; б) 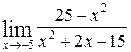 .
.
49. а) 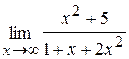 ; б)
; б) 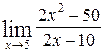 .
.
50. а) 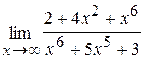 ; б)
; б) 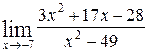 .
.
Пример.
а) При 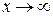 числитель и знаменатель дроби стремятся к
числитель и знаменатель дроби стремятся к 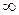 . Чтобы раскрыть неопределенность
. Чтобы раскрыть неопределенность  , нужно числитель и знаменатель разделить на старшую степень х.
, нужно числитель и знаменатель разделить на старшую степень х.
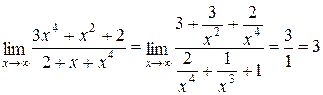 .
.
б) Имеем неопределенность вида 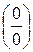 . Чтобы избавиться от иррациональности в знаменателе, разложим числитель и знаменатель дроби на множители, при этом воспользуемся формулой разности квадратов
. Чтобы избавиться от иррациональности в знаменателе, разложим числитель и знаменатель дроби на множители, при этом воспользуемся формулой разности квадратов
 . (1)
. (1)
Также будем использовать формулу для разложения квадратного трехчлена на множители:
 , (2)
, (2)
где 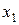 ,
, 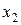 - корни соответствующего квадратного уравнения.
- корни соответствующего квадратного уравнения.
Итак, найдем корни квадратного уравнения 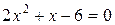 . Для этого сначала вычислим его дискриминант по формуле:
. Для этого сначала вычислим его дискриминант по формуле:
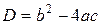 . Итак,
. Итак, 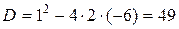 . Найдем корни уравнения по формулам:
. Найдем корни уравнения по формулам:
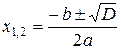 . Получим:
. Получим:  ,
, 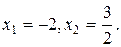
Таким образом, по формуле (2) получаем:

По формуле (1) разложим выражение:
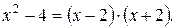 Таким образом, искомый предел:
Таким образом, искомый предел:
 .
.
Производная
51-60. Найти производные 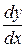 данных функций.
данных функций.
51. а) 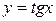 ; б)
; б) 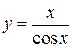 ; в)
; в) 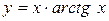 .
.
52. а) 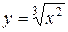 ; б)
; б)  ; в)
; в) 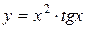 .
.
53. а) 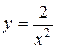 ; б)
; б) 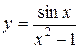 ; в)
; в) 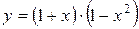 .
.
54. а)  ; б)
; б) 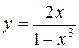 ; в)
; в) 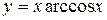 .
.
55. а) 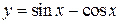 ; б)
; б) 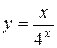 ; в)
; в) 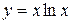 .
.
56. а) 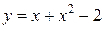 ; б)
; б) 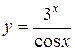 ; в)
; в) 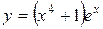 .
.
57. а) 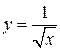 ; б)
; б) 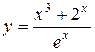 ; в)
; в) 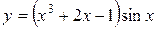 .
.
58. а) 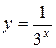 ; б)
; б) 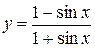 ; в)
; в) 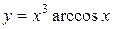 .
.
59. а)  ; б)
; б) 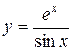 ; в)
; в) 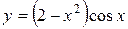 .
.
60. а) 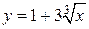 ; б)
; б) 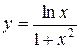 ; в)
; в) 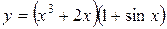 .
.
Пример.
а) 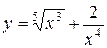 .
.
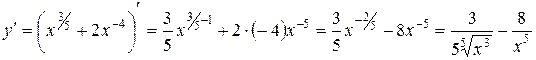 .
.
б)  .
.
Воспользуемся формулами для производной суммы двух функций и их произведения:

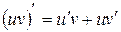 .
.
Будем иметь:
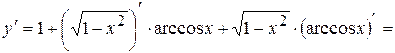
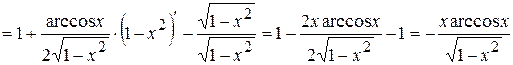 .
.
в) 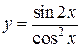 .
.
Применим правило дифференцирования частного двух функций:
 .
.
Будем иметь:
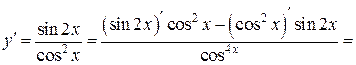
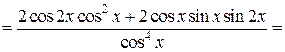
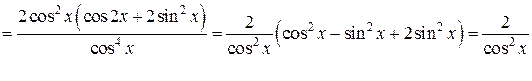 .
.
Приложения производной
61-70. Задана функция.
а) исследуйте функцию на возрастание и убывание;
б) найдите экстремумы функций.
61. 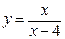 . 66.
. 66. 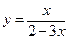 .
.
62. 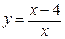 . 67.
. 67.  .
.
63. 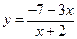 . 68.
. 68. 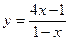 .
.
64. 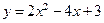 . 69.
. 69. 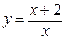 .
.
65. 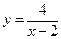 . 70.
. 70. 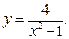
Пример. 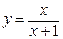 .
.
Представим сначала схему исследования функции на монотонность и экстремумы.
1) найти область определения и интервалы, на которых функция непрерывна.
2) найти производную
3) найти критические точки, то есть внутренние точки области определения, в которых производная функции равна нулю или не существует
4) обозначить критические точки на области определения, найти знак производной и характер поведения функции на каждом из интервалов, на которые критические точки разбивают область определения.
5) определить относительно каждой критической точки является ли она точкой максимума, минимума или не является точкой экстремума.
6) записать результат исследования функции: промежутки монотонности и экстремумы.
Итак,
1) 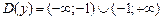
2) 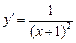 ,
, 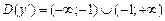 ,
, 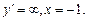
3)Наносим критические точки на координатную прямую. Производная везде в окрестности точки 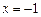 будет иметь знак «+», значит функция возрастает на всей числовой прямой, за исключением точки
будет иметь знак «+», значит функция возрастает на всей числовой прямой, за исключением точки 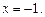 Таким образом,
Таким образом, 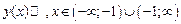 , экстремумов нет.
, экстремумов нет.
Приложение производной в экономике
71-80. Найти оптимальный объём производства фирмы, функция чистой прибыли которой задана 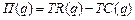 ,
, 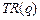 - прибыль фирмы,
- прибыль фирмы, 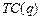 - издержки фирмы.
- издержки фирмы.
71. 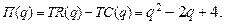 76.
76. 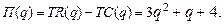
72.  77.
77. 
73. 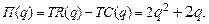 78.
78. 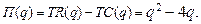
74. 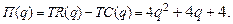 79.
79. 
75. 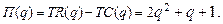 80.
80. 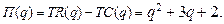
Пример. Найти оптимальный объём производства фирмы, функция чистой прибыли которой задана 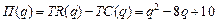 ,
, 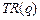 - прибыль фирмы,
- прибыль фирмы, 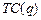 - издержки фирмы.
- издержки фирмы.
Найдем производную данной функции: 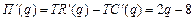 Приравняем производную к нулю и найдём точку экстремума:
Приравняем производную к нулю и найдём точку экстремума: 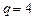 . Является ли объём выпуска, равный четырём единицам продукции, оптимальным для фирмы? Чтобы ответить на этот вопрос, надо проанализировать характер изменения знака производной при переходе через точку экстремума.
. Является ли объём выпуска, равный четырём единицам продукции, оптимальным для фирмы? Чтобы ответить на этот вопрос, надо проанализировать характер изменения знака производной при переходе через точку экстремума.
При 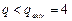 ,
, 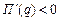 и прибыль убывает.
и прибыль убывает.
При 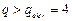 ,
, 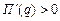 и прибыль возрастает. Как видим, при переходе через точку экстремума производная меняет свой знак с минуса на плюс. Следовательно, в точке экстремума прибыль принимает минимальное значение, и таким образом, этот объём производства не является оптимальным для фирмы. Каким же всё-таки будет оптимальный объём выпуска для данной фирмы? Ответ на этот вопрос зависит от дополнительного исследования производственных возможностей фирмы. Если фирма не может производить за рассматриваемый период больше 8 единиц продукции (
и прибыль возрастает. Как видим, при переходе через точку экстремума производная меняет свой знак с минуса на плюс. Следовательно, в точке экстремума прибыль принимает минимальное значение, и таким образом, этот объём производства не является оптимальным для фирмы. Каким же всё-таки будет оптимальный объём выпуска для данной фирмы? Ответ на этот вопрос зависит от дополнительного исследования производственных возможностей фирмы. Если фирма не может производить за рассматриваемый период больше 8 единиц продукции ( 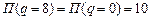 ), то оптимальным решением для фирмы будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и/или оборудования. Если же фирма способна производить за рассматриваемый период больше 8 единиц продукции, то оптимальным решением для фирмы будет выпуск на пределе своих производственных возможностей.
), то оптимальным решением для фирмы будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и/или оборудования. Если же фирма способна производить за рассматриваемый период больше 8 единиц продукции, то оптимальным решением для фирмы будет выпуск на пределе своих производственных возможностей.
81-90. Найти объём производства, при котором фирма, действующая на рынке совершенной конкуренции, будет получать максимальную прибыль, если цена продукта составит 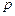 , а издержки на его производство заданы функцией
, а издержки на его производство заданы функцией 
81.  86.
86. 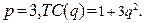
82.  87.
87. 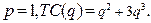
83. 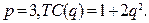 88.
88. 
84. 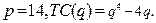 89.
89. 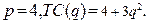
85. 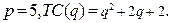 90.
90. 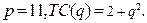
Пример. Найти объём производства, при котором фирма, действующая на рынке совершенной конкуренции, будет получать максимальную прибыль, если 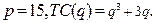
Прибыль фирмы, действующей на рынке совершенной конкуренции, максимизируется при равенстве предельной выручки и предельных издержек: 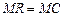 . Поскольку при совершенной конкуренции наблюдается равенство цены и предельной выручки:
. Поскольку при совершенной конкуренции наблюдается равенство цены и предельной выручки: 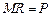 , то можно утверждать, что фирма максимизирует прибыль при
, то можно утверждать, что фирма максимизирует прибыль при 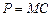 .Найдем предельные издержки:
.Найдем предельные издержки: 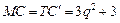 ,
, 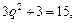
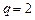 . Таким образом, при цене
. Таким образом, при цене 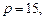 фирма предложит 2 единицы продукции.
фирма предложит 2 единицы продукции.
Дата: 2018-11-18, просмотров: 371.