Чтение учебника
1. Изучая материал по учебнику, следует переходить к следующему вопросу только после правильного понимания предыдущего, производя на бумаге все вычисления (в том числе и те, которые ради краткости опущены в учебнике) и выполняя имеющиеся в учебнике чертежи.
2. Особое внимание следует обращать на определение основных понятий. Студент должен подробно разбирать примеры, которые поясняют такие определения, и уметь строить аналогичные примеры самостоятельно.
3. Необходимо помнить, что каждая теорема состоит из предположений и утверждения. Все предположения должны обязательно использоваться в доказательстве. Нужно добиваться точного представления о том, в каком месте доказательства использовано каждое предположение теоремы. Полезно составлять схемы доказательств сложных теорем. Правильному пониманию многих теорем помогает разбор примеров математических объектов, обладающих и не обладающих свойствами, указанными в предположениях и утверждениях теорем.
4. При изучении материала по учебнику полезно вести конспект, в который рекомендуется вписывать определения, формулировки теорем, формулы, уравнения и т. д. На полях конспекта следует отмечать вопросы, выделенные студентом для получения письменной или устной консультации преподавателя.
5. Письменное оформление работы студента имеет исключительно важное значение. Записи в конспекте должны быть сделаны чисто, аккуратно и расположены в определенном порядке. Хорошее внешнее оформление конспекта по изученному материалу не только приучит студента к необходимому в работе порядку, но и позволит ему избежать многочисленных ошибок, которые происходят из-за небрежных, беспорядочных записей.
6. Выводы, полученные в виде формул, рекомендуется в конспекте подчеркивать или обводить рамкой, чтобы при перечитывании конспекта они выделялись и лучше запоминались. Опыт показывает, что многим студентам помогает в работе составление списка, содержащего важнейшие и наиболее часто употребляемые формулы курса. Такой список не только помогает запомнить формулы, но и может служить постоянным справочником для студента.
Решение задач
1. Чтение учебника должно сопровождаться решением задач, для чего рекомендуется завести специальную тетрадь.
2. При решении задач нужно обосновывать каждый этап решения исходя из теоретических положений курса. Если студент видит несколько путей решения, то он должен сравнить их и выбрать из них самый лучший. Полезно до начала вычислений составить краткий план решения.
3. Решения задач и примеров следует излагать подробно, а вычисления в строгом порядке, отделяя вспомогательные вычисления от основных. Чертежи можно выполнять от руки, но аккуратно и в соответствии с данными условиями. Если чертеж требует особо тщательного выполнения (например, при графической проверке решения, полученного путем вычислений), то следует пользоваться линейкой, транспортиром, лекалом и указывать масштаб.
4. Решение каждой задачи должно доводиться до ответа, требуемого условием, и по возможности с выводом формулы в общем виде. Затем в полученную формулу подставляют числовые значения (если они даны). В промежуточных вычислениях не следует вводить приближенные значения корней, числа p и т. п.
5. Полученный ответ следует проверять способами, вытекающими из существа данной задачи. Если, например, решалась задача с конкретным физическим или геометрическим содержанием, то полезно, прежде всего, проверить размерность полученного ответа. Полезно также, если возможно, решить задачу несколькими способами и сравнить полученные результаты.
6. Решение задач определенного типа нужно продолжать до приобретения устойчивых навыков в их решении.
Самопроверка
1. После изучения определенной темы по учебнику и решения достаточного количества соответствующих задач студенту рекомендуется воспроизвести по памяти определения, выводы формул, формулировки и доказательства теорем. Вопросы для самопроверки, приведенные в настоящем пособии, даны с целью помочь студенту в повторении, закреплении и проверке прочности усвоения изученного материала. В случае необходимости надо еще раз внимательно разобраться в материале учебника, решить ряд задач.
2. Иногда недостаточность усвоения того или иного вопроса выясняется только при изучении дальнейшего материала. В этом случае надо вернуться назад и повторить плохо усвоенный раздел.
3. Важным критерием усвоения теории является умение решать задачи на пройденный материал. Однако здесь следует предостеречь студента от весьма распространенной ошибки, заключающейся в том, что благополучное решение задач воспринимается им как признак усвоения теории. Часто правильное решение задачи получается в результате применения механически заученных формул, без понимания существа дела. Можно сказать, что умение решать задачи является необходимым, но недостаточным признаком хорошего знания теории.
Консультации
1. Если в процессе работы над изучением теоретического материала или при решении задач у студента возникают вопросы, разрешить которые самостоятельно не удается (неясность терминов, формулировок теорем, отдельных задач и др.), то он может обратиться к преподавателю для получения от него письменной или устной консультации.
2. В своих вопросах студент должен точно указать, в чем он испытывает затруднение. Если он не разобрался в теоретических объяснениях, или в доказательстве теоремы, или в выводе формулы по учебнику, то нужно указать, какой это учебник, год его издания и страницу, где рассмотрен затрудняющий его вопрос, и что именно его затрудняет. Если студент испытывает затруднение при решении задачи, то следует указать характер этого затруднения, привести предполагаемый план решения.
3. За консультацией следует обращаться и при сомнении в правильности ответов на вопросы для самопроверки.
Контрольные работы
1. В процессе изучения курса математики студент должен выполнить ряд контрольных работ, главная цель которых – оказать студенту помощь в его работе. Рецензии на эти работы позволяют студенту судить о степени усвоения им соответствующего раздела курса; указывают на имеющиеся у него пробелы в знаниях, на желательное направление дальнейшей работы; помогают сформулировать вопросы для постановки их перед преподавателем.
2. Не следует приступать к выполнению контрольного задания, не решив достаточного количества задач по материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания вызывается тем, что студент не выполнил это требование.
3. Контрольные работы должны выполняться самостоятельно. Несамостоятельно выполненная работа не дает возможности преподавателю-рецензенту указать студенту на недостатки в его работе, в усвоении им учебного материала, в результате чего студент не приобретает необходимых знаний и может оказаться неподготовленным к устному зачету и экзамену.
4. Не рекомендуется присылать в академию одновременно работы по нескольким заданиям: это не дает возможности рецензенту своевременно указать студенту на допущенные им ошибки и удлиняет срок рецензирования работ.
5. Прорецензированные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять. Без предъявления прорецензированных работ студент не допускается к сдаче зачета и экзамена.
Зачеты и экзамены
На экзаменах и зачетах выясняется, прежде всего, отчетливое усвоение всех теоретических и практических вопросов программы и умение применять полученные знания к решению практических задач. Определения, теоремы, правила должны формулироваться точно и с пониманием существа дела; решение задач в простейших случаях должно выполняться без ошибок и уверенно; всякая письменная и графическая работа должна быть сделана аккуратно и четко. Только при выполнении этих условий знания могут быть признаны удовлетворяющими требованиям, предъявляемым программой.
При подготовке к экзамену учебный материал рекомендуется повторить по учебнику и конспекту.
Вопросы для самопроверки
Литература
1. Ильин В.А., Позняк Э.Г.. Аналитическая геометрия.— М.: Наука, 1981.
2. Ефимов Н.В. Краткий курс аналитической геометрии. — М.: Наука, 1967.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.— М.: Высшая школа, 1967-1971. Ч. I, II, III.
4. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов.— М.: Наука, 1970—1985, т. 1, 2.
5. Шкіль М.І., Колесник Т.В., Котлова В.М.. Вища математика.– К.: Либідь, 1994. Т. 1-3.
6. Мышкис А.Д. Лекции по высшей математике — М.: Наука, 1967.
7. Привалов И.И. Аналитическая геометрия.— М., 1956.
8. Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах.— М.: Высшая школа, 1985.
9. Каплан И.А. Практические занятия по высшей математике. – Харьков, 1967.
10. Шестаков А.А., Малышева И.А., Полозков Д.П. Курс высшей математики.— М.: Высшая школа, 1987.
11. Бермант А.Ф., Абрамович И.Г. Краткий курс математического анализа.— М.: Наука, 1973.
12. Мантуров О.В., Матвеев Н.М. Курс высшей математики.— М.: Высшая школа, 1986.
13. Самойленко А.М., Перестюк М.О., Парасюк І.О. Диференціальні рівняння.— К.: Либідь, 1994.
14. Запорожец Г.И. Руководство к решению задач по математическому анализу.— М.: Высшая школа, 1966.
15. Гмурман В.Е. Теория вероятностей и математическая статистика.— М.: Высшая школа, 1972.
16. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.— М.: Высшая школа, 1975.
17. Гурский Е.И. Теория вероятностей с элементами математической статистики. – М.: Высшая школа, 1971.
18. Вентцель Е.С., Овчаров Л.А. Теория вероятностей. Задачи и упражнения.— М.: Наука, 1969.
19. Овчинников П.Ф., Яремчук Ф.П., Михайленко В.М. Высшая математика. — К.: Вища школа, 1987.
20. Высшая математика. Сборник задач / под ред. Овчинникова П.Ф.. — К.: Вища школа, 1991.
21. Герасимчук В.С., Васильченко Г.С., Кравцов В.И. Курс классической математики в примерах и задачах. Ч.1, Донецк. Норд-компьютер, 2002, 528с.
22. Герасимчук В.С., Васильченко Г.С., Кравцов В.И. Курс классической математики в примерах и задачах. Ч.2, Донецк. Норд-компьютер, 2004, 458с.
Элементы линейной алгебры
21-30. Решить системы линейных уравнений методом Гаусса, Крамера.
21. 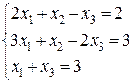 22.
22. 
23. 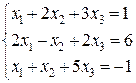 24.
24. 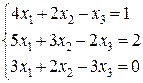
25. 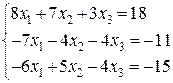 26.
26. 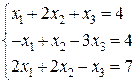
27. 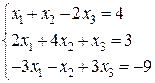 28.
28. 
29. 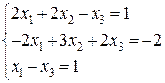 30.
30. 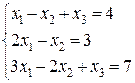
Пример. Решить систему линейных уравнений методом Гаусса и Крамера:

Метод Гаусса.
1. Составляем расширенную матрицу системы и приводим ее к ступенчатому виду, проводя преобразования над строками, позволяющие получить эквивалентную систему (перестановка строк, умножение элементов строк на любое отличное от нуля число, прибавление или вычитание соответствующих элементов строк):
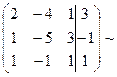
2. Выделяем лидеров строк. Лидер строки - первый ненулевой элемент строки.
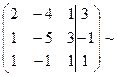
3. При необходимости меняем строки в расширенной матрице системы так, чтобы лидер в строке с наименьшим номером был равен 1. (Перестановка строк в расширенной матрице соответствует перестановке уравнений в системе, а, следовательно, при перестановке строк в матрице мы получим эквивалентную систему). Переставим первое и третье уравнение системы.
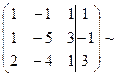
4. Обнуляем лидеров строк, стоящих в строках с большим номером, воспользовавшись элементарными математическими преобразованиями –умножением строки на число, сложение и вычитание строк. Для этого умножим первую строку на (-1) и складываем со второй строкой, затем необходимо первую строку умножить на (-2) и сложить с третьей строкой.
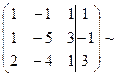
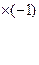
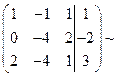
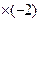
5. После обнуления, снова выделяем лидеров строк.
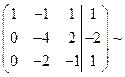
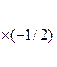
6. Снова обнуляем лидеров строк стоящих в строках с большим номером.
Умножим вторую строку на (-1/2) и сложим с третьей строкой

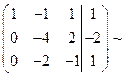
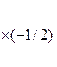
7. Привели матрицу к ступенчатому виду.
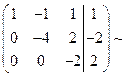
8. Восстанавливаем по приведенной матрице систему. При этом напомним, что третий столбец соответствует коэффициентам, стоящим при неизвестном  , второй - при
, второй - при 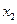 и первый -
и первый - 
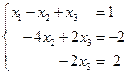
9. Решаем полученную систему и находим неизвестные.
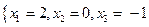
Метод Крамера.
1. Составляем определитель матрицы системы, который составляют из коэффициентов системы уравнений. Для этого выписываем коэффициенты: первое уравнение системы имеет при переменной 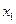 коэффициент 2, при
коэффициент 2, при 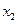 - коэффициент – (-4), при
- коэффициент – (-4), при  - коэффициент 1.
- коэффициент 1.
Записываем все эти коэффициенты в первую строку определителя основной матрицы, коэффициенты второго уравнения во вторую строку и третью соответственно.
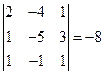 .
.
2. Теперь найдем: ∆ 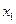 . Для этого первый столбец заменяем столбцом свободных членов.
. Для этого первый столбец заменяем столбцом свободных членов.
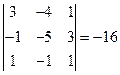 .
.
3. Теперь найдем: ∆ 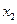 . Для этого второй столбец заменяем столбцом свободных членов.
. Для этого второй столбец заменяем столбцом свободных членов.
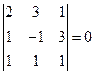 .
.
4. Аналогично находим ∆  . Для этого третий столбец заменяем столбцом свободных членов.
. Для этого третий столбец заменяем столбцом свободных членов.
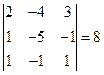 .
.
5. Пользуемся формулами для нахождения неизвестных переменных
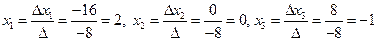
Раздел Функция.
31-40. Задана функция.
а) найдите область определения и множество значений функции;
б) исследуйте функцию на четность и нечетность.
31.  . 36.
. 36. 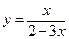 .
.
32. 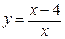 . 37.
. 37. 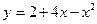 .
.
33. 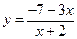 . 38.
. 38. 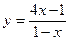 .
.
34. 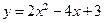 . 39.
. 39. 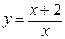 .
.
35. 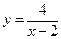 . 40.
. 40. 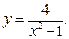
Пример. 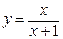 .
.
а) Найдем сначала область определения данной функции. Числитель данной дроби не содержит никаких особенностей, а вот знаменатель должен быть ненулевым. Давайте приравняем его к нулю и попытаемся найти «плохие» точки: 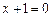 ,
, 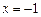 . Данное значение не входит в область определения функции. Действительно, подставьте
. Данное значение не входит в область определения функции. Действительно, подставьте 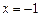 в функцию и вы увидите, что знаменатель обращается в ноль, а на ноль, как известно, делить нельзя. Таким образом, областью определения данной функции, обозначаемая
в функцию и вы увидите, что знаменатель обращается в ноль, а на ноль, как известно, делить нельзя. Таким образом, областью определения данной функции, обозначаемая 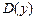 , будет
, будет 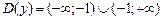 .
.
Теперь найдем множество значений данной функции. Как нетрудно убедиться, исходную функцию можно переписать в виде: 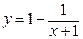 , график которой можно получить из графика функции
, график которой можно получить из графика функции 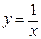 следующими преобразованиями: сдвигом на 1 единицу влево, симметричным отображением относительно Ox и сдвигом на 1 единичный отрезок вверх по оси Oy. Таким образом, областью значений данной функции будет
следующими преобразованиями: сдвигом на 1 единицу влево, симметричным отображением относительно Ox и сдвигом на 1 единичный отрезок вверх по оси Oy. Таким образом, областью значений данной функции будет  .
.
б)Исследуем функцию на четность и нечетность. Найдем 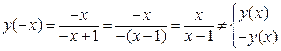
Таким образом, функция не является ни четной, ни нечетной и, значит, данная функция является функцией общего вида.
41-50. Найти пределы функций, не пользуясь правилом Лопиталя.
41. а) 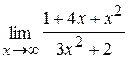 ; б)
; б) 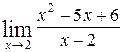 .
.
42. а) 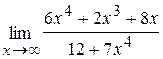 ; б)
; б) 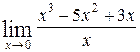 .
.
43. а) 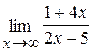 ; б)
; б) 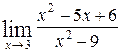 .
.
44. а) 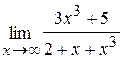 ; б)
; б) 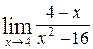 .
.
45. а) 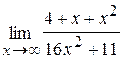 ; б)
; б) 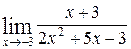 .
.
46. а) 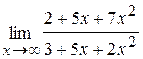 ; б)
; б) 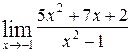 .
.
47. а) 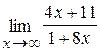 ; б)
; б) 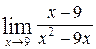 .
.
48. а) 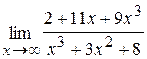 ; б)
; б) 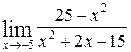 .
.
49. а) 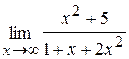 ; б)
; б) 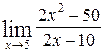 .
.
50. а) 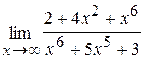 ; б)
; б) 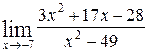 .
.
Пример.
а) При 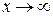 числитель и знаменатель дроби стремятся к
числитель и знаменатель дроби стремятся к 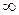 . Чтобы раскрыть неопределенность
. Чтобы раскрыть неопределенность  , нужно числитель и знаменатель разделить на старшую степень х.
, нужно числитель и знаменатель разделить на старшую степень х.
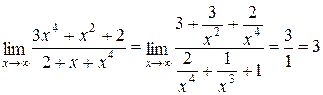 .
.
б) Имеем неопределенность вида 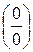 . Чтобы избавиться от иррациональности в знаменателе, разложим числитель и знаменатель дроби на множители, при этом воспользуемся формулой разности квадратов
. Чтобы избавиться от иррациональности в знаменателе, разложим числитель и знаменатель дроби на множители, при этом воспользуемся формулой разности квадратов
 . (1)
. (1)
Также будем использовать формулу для разложения квадратного трехчлена на множители:
 , (2)
, (2)
где  ,
, 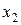 - корни соответствующего квадратного уравнения.
- корни соответствующего квадратного уравнения.
Итак, найдем корни квадратного уравнения 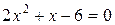 . Для этого сначала вычислим его дискриминант по формуле:
. Для этого сначала вычислим его дискриминант по формуле:
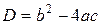 . Итак,
. Итак, 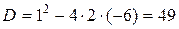 . Найдем корни уравнения по формулам:
. Найдем корни уравнения по формулам:
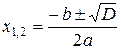 . Получим:
. Получим:  ,
, 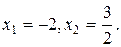
Таким образом, по формуле (2) получаем:

По формуле (1) разложим выражение:
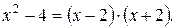 Таким образом, искомый предел:
Таким образом, искомый предел:
 .
.
Производная
51-60. Найти производные 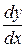 данных функций.
данных функций.
51. а) 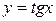 ; б)
; б) 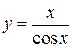 ; в)
; в) 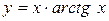 .
.
52. а) 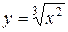 ; б)
; б)  ; в)
; в) 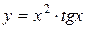 .
.
53. а) 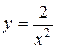 ; б)
; б) 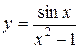 ; в)
; в) 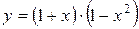 .
.
54. а)  ; б)
; б) 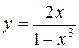 ; в)
; в) 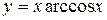 .
.
55. а) 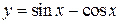 ; б)
; б) 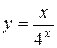 ; в)
; в) 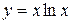 .
.
56. а) 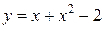 ; б)
; б) 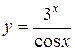 ; в)
; в) 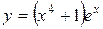 .
.
57. а) 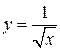 ; б)
; б) 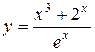 ; в)
; в) 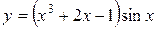 .
.
58. а) 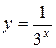 ; б)
; б) 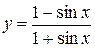 ; в)
; в) 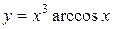 .
.
59. а)  ; б)
; б) 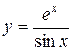 ; в)
; в) 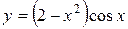 .
.
60. а) 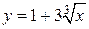 ; б)
; б) 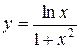 ; в)
; в) 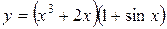 .
.
Пример.
а) 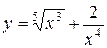 .
.
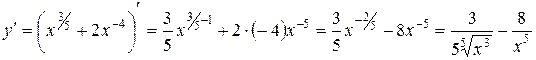 .
.
б)  .
.
Воспользуемся формулами для производной суммы двух функций и их произведения:

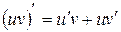 .
.
Будем иметь:
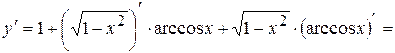
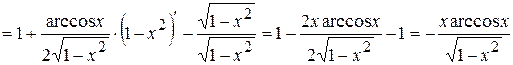 .
.
в) 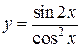 .
.
Применим правило дифференцирования частного двух функций:
 .
.
Будем иметь:
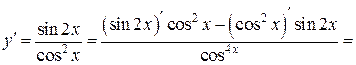
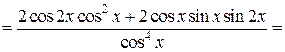
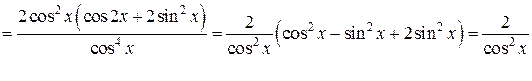 .
.
Приложения производной
61-70. Задана функция.
а) исследуйте функцию на возрастание и убывание;
б) найдите экстремумы функций.
61. 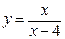 . 66.
. 66. 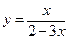 .
.
62. 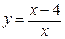 . 67.
. 67.  .
.
63. 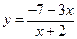 . 68.
. 68. 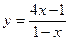 .
.
64. 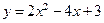 . 69.
. 69. 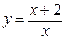 .
.
65. 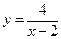 . 70.
. 70. 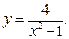
Пример. 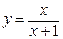 .
.
Представим сначала схему исследования функции на монотонность и экстремумы.
1) найти область определения и интервалы, на которых функция непрерывна.
2) найти производную
3) найти критические точки, то есть внутренние точки области определения, в которых производная функции равна нулю или не существует
4) обозначить критические точки на области определения, найти знак производной и характер поведения функции на каждом из интервалов, на которые критические точки разбивают область определения.
5) определить относительно каждой критической точки является ли она точкой максимума, минимума или не является точкой экстремума.
6) записать результат исследования функции: промежутки монотонности и экстремумы.
Итак,
1) 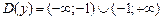
2) 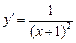 ,
, 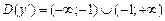 ,
, 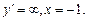
3)Наносим критические точки на координатную прямую. Производная везде в окрестности точки 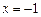 будет иметь знак «+», значит функция возрастает на всей числовой прямой, за исключением точки
будет иметь знак «+», значит функция возрастает на всей числовой прямой, за исключением точки 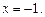 Таким образом,
Таким образом, 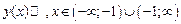 , экстремумов нет.
, экстремумов нет.
Приложение производной в экономике
71-80. Найти оптимальный объём производства фирмы, функция чистой прибыли которой задана 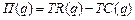 ,
, 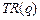 - прибыль фирмы,
- прибыль фирмы, 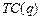 - издержки фирмы.
- издержки фирмы.
71. 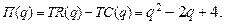 76.
76. 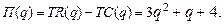
72.  77.
77. 
73. 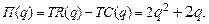 78.
78. 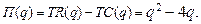
74. 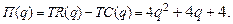 79.
79. 
75. 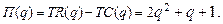 80.
80. 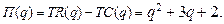
Пример. Найти оптимальный объём производства фирмы, функция чистой прибыли которой задана 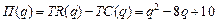 ,
, 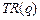 - прибыль фирмы,
- прибыль фирмы, 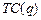 - издержки фирмы.
- издержки фирмы.
Найдем производную данной функции: 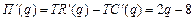 Приравняем производную к нулю и найдём точку экстремума:
Приравняем производную к нулю и найдём точку экстремума: 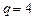 . Является ли объём выпуска, равный четырём единицам продукции, оптимальным для фирмы? Чтобы ответить на этот вопрос, надо проанализировать характер изменения знака производной при переходе через точку экстремума.
. Является ли объём выпуска, равный четырём единицам продукции, оптимальным для фирмы? Чтобы ответить на этот вопрос, надо проанализировать характер изменения знака производной при переходе через точку экстремума.
При 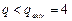 ,
, 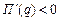 и прибыль убывает.
и прибыль убывает.
При 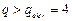 ,
, 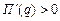 и прибыль возрастает. Как видим, при переходе через точку экстремума производная меняет свой знак с минуса на плюс. Следовательно, в точке экстремума прибыль принимает минимальное значение, и таким образом, этот объём производства не является оптимальным для фирмы. Каким же всё-таки будет оптимальный объём выпуска для данной фирмы? Ответ на этот вопрос зависит от дополнительного исследования производственных возможностей фирмы. Если фирма не может производить за рассматриваемый период больше 8 единиц продукции (
и прибыль возрастает. Как видим, при переходе через точку экстремума производная меняет свой знак с минуса на плюс. Следовательно, в точке экстремума прибыль принимает минимальное значение, и таким образом, этот объём производства не является оптимальным для фирмы. Каким же всё-таки будет оптимальный объём выпуска для данной фирмы? Ответ на этот вопрос зависит от дополнительного исследования производственных возможностей фирмы. Если фирма не может производить за рассматриваемый период больше 8 единиц продукции ( 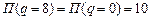 ), то оптимальным решением для фирмы будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и/или оборудования. Если же фирма способна производить за рассматриваемый период больше 8 единиц продукции, то оптимальным решением для фирмы будет выпуск на пределе своих производственных возможностей.
), то оптимальным решением для фирмы будет вообще ничего не производить, а получать доход от сдачи в аренду помещений и/или оборудования. Если же фирма способна производить за рассматриваемый период больше 8 единиц продукции, то оптимальным решением для фирмы будет выпуск на пределе своих производственных возможностей.
81-90. Найти объём производства, при котором фирма, действующая на рынке совершенной конкуренции, будет получать максимальную прибыль, если цена продукта составит 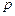 , а издержки на его производство заданы функцией
, а издержки на его производство заданы функцией 
81.  86.
86. 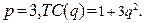
82.  87.
87. 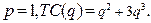
83. 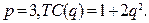 88.
88. 
84. 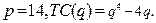 89.
89. 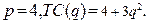
85. 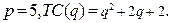 90.
90. 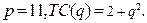
Пример. Найти объём производства, при котором фирма, действующая на рынке совершенной конкуренции, будет получать максимальную прибыль, если 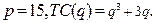
Прибыль фирмы, действующей на рынке совершенной конкуренции, максимизируется при равенстве предельной выручки и предельных издержек: 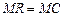 . Поскольку при совершенной конкуренции наблюдается равенство цены и предельной выручки:
. Поскольку при совершенной конкуренции наблюдается равенство цены и предельной выручки: 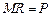 , то можно утверждать, что фирма максимизирует прибыль при
, то можно утверждать, что фирма максимизирует прибыль при 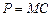 .Найдем предельные издержки:
.Найдем предельные издержки: 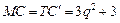 ,
, 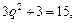
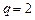 . Таким образом, при цене
. Таким образом, при цене 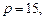 фирма предложит 2 единицы продукции.
фирма предложит 2 единицы продукции.
Пример.
а) 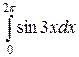 . Применяя формулу Ньютона-Лейбница, вычислим этот интеграл:
. Применяя формулу Ньютона-Лейбница, вычислим этот интеграл:
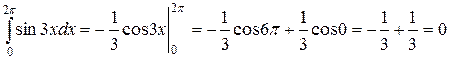
б) 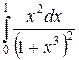 . Вычислим этот интеграл, используя метод замены переменной:
. Вычислим этот интеграл, используя метод замены переменной:

в) 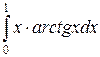 . Применяя формулу интегрирования по частям получим:
. Применяя формулу интегрирования по частям получим:
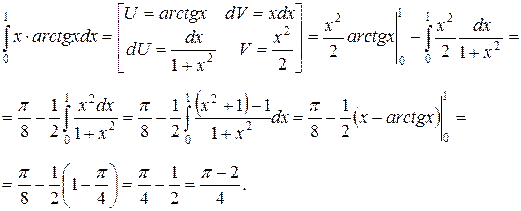
121.-130. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
121. 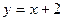 ,
,  . 12 6.
. 12 6. 
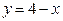
122 . 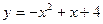 ,
, 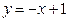 . 12 7.
. 12 7. 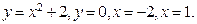
123. 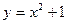 ,
, 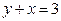 . 12 8.
. 12 8. 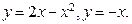
124. 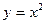 ,
, 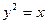 . 12 9.
. 12 9. 
125. 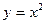 ,
,  . 1 3 0.
. 1 3 0. 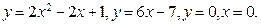
Пример.
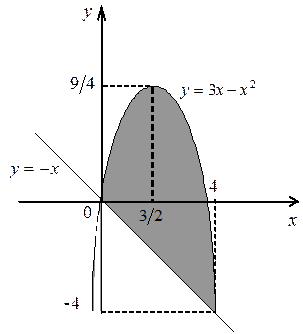
а) Вычислить площадь фигуры, ограниченной параболой 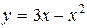 и прямой
и прямой  .
.
Находим точки пересечения данных кривых и строим искомую фигуру
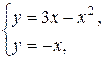
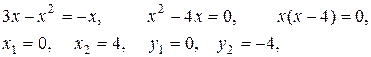
Площадь фигуры, ограниченной снизу кривой 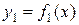 , сверху – кривой
, сверху – кривой 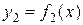 , вычисляет интеграл
, вычисляет интеграл 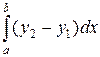 , где
, где  и
и 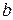 - абсциссы точек пересечения этих кривых, причем
- абсциссы точек пересечения этих кривых, причем 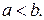
Следовательно, имеем
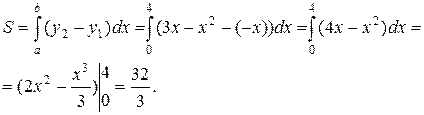
Дифференциальные уравнения.
131 – 140. Найти общее решение дифференциального уравнения.
131. а). 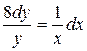 ; б).
; б). 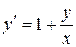 ; в).
; в). 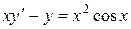 .
.
132. а). 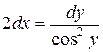 ; б).
; б). 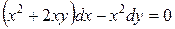 ; в).
; в). 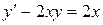 .
.
133. а).  ; б).
; б). 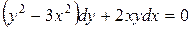 ; в).
; в). 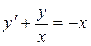 .
.
134. а). 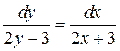 ; б).
; б). 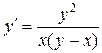 ; в).
; в). 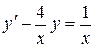 .
.
135. а).  ; б).
; б). 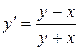 ; в).
; в). 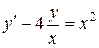 .
.
136. а). 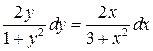 ; б).
; б).  ; в).
; в). 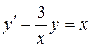 .
.
137. а).  ; б).
; б).  ; в).
; в). 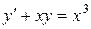 .
.
138. а).  ; б).
; б). 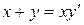 ; в).
; в). 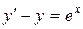 .
.
139. а). 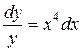 ; б).
; б). 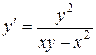 ; в).
; в). 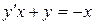 .
.
140. а). 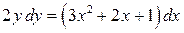 ; б).
; б). 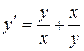 ; в).
; в). 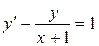 .
.
Пример.
а) 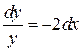 .
.
Данное уравнение является уравнением с разделенными переменными. Проинтегрируем обе его части:
 , получим:
, получим: 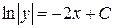 .
.
б). 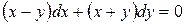 .
.
Для решения данного уравнения используем тот факт, что 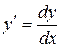 . Так как переменные в данном случае разделить нельзя, то выразим
. Так как переменные в данном случае разделить нельзя, то выразим 
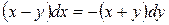 , отсюда по правилу пропорции получаем:
, отсюда по правилу пропорции получаем:
 , или
, или 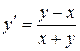 .
.
В данном случае 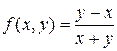 ;
; 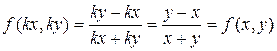 .
.
Следовательно, данное уравнение – однородное. Делаем замену переменной
 ,
, 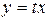 ,
, 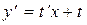 . После замены получим:
. После замены получим:
 ,
,  ,
,  .
.
Получили уравнение с разделяющимися переменными. Разделяя переменные, получим: 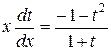 ,
,  .
.
Интегрируя, находим общее решение
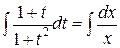 ,
, 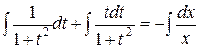 ,
,
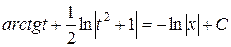 .
.
Возвращаясь к старой переменной, получаем общий интеграл
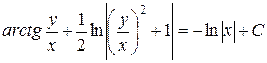 .
.
в). 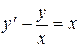 .
.
Данное уравнение линейное. Ищем решение в виде 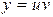 ,
, 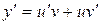 .
.
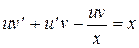 ,
, 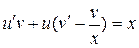 .
.
Решаем уравнение. 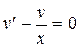 ,
, 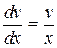 ,
, 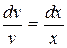 ,
, 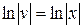 ,
, 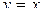 .
.
Подставляя полученное значение 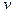 в уравнение, имеем:
в уравнение, имеем:
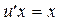 ,
, 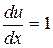 ,
, 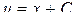 .
.
Общее решение 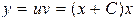 или
или 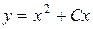 .
.
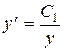 ,
,  ,
, 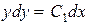 ,
, 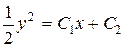 .
.
141–150. Найти общее решение дифференциального уравнения:
141. а). 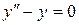 ; б).
; б). 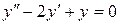 ; в).
; в). 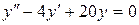 .
.
142. а). 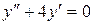 ; б).
; б). 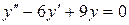 ; в).
; в). 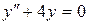 .
.
143. а).  ; б).
; б). 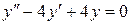 ; в).
; в). 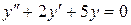 .
.
144. а). 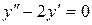 ; б).
; б). 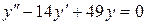 ; в).
; в). 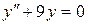 .
.
145. а). 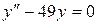 ; б).
; б). 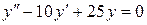 ; в).
; в).  .
.
146. а). 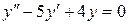 ; б).
; б).  ; в).
; в). 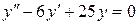 .
.
147. а).  ; б).
; б). 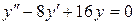 ; в).
; в). 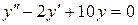 .
.
148. а). 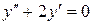 ; б).
; б). 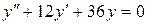 ; в).
; в). 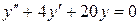 .
.
149. а). 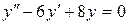 ; б).
; б).  ; в).
; в). 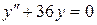 .
.
150. а). 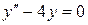 ; б).
; б). 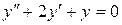 ; в).
; в). 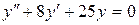 .
.
Пример. а). 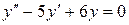 .
.
Составим соответствующее характеристическое уравнение:
 ,
,
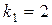 ,
, 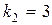 .
.
Так как корни характеристического уравнения 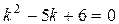 действительные, различные, следовательно, общее решение однородного уравнения имеет вид
действительные, различные, следовательно, общее решение однородного уравнения имеет вид 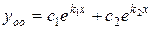 , то есть имеем
, то есть имеем
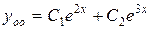 .
.
б). 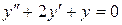 .
.
Составим соответствующее характеристическое уравнение:
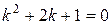 ,
,
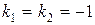 .
.
Так как корни характеристического уравнения  действительные, одинаковые, следовательно, общее решение однородного уравнения имеет вид
действительные, одинаковые, следовательно, общее решение однородного уравнения имеет вид  , то есть имеем
, то есть имеем
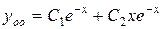 .
.
в). 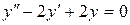 .
.
Составим соответствующее характеристическое уравнение:
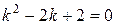 . Решим его при помощи вычисления дискриминанта:
. Решим его при помощи вычисления дискриминанта:
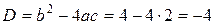 . Так как в данном случае
. Так как в данном случае 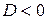 , то для вычисления квадратного корня
, то для вычисления квадратного корня 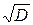 используем равенство
используем равенство 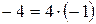 . Так как
. Так как 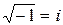 (комплексная единица), то в данном случае
(комплексная единица), то в данном случае 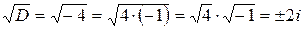 . Таким образом, имеем в данном случае комплексные корни:
. Таким образом, имеем в данном случае комплексные корни:
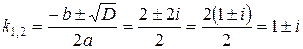 .
.
Так как корни характеристического уравнения 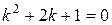 комплексно-сопряженные, следовательно, общее решение однородного уравнения имеет вид
комплексно-сопряженные, следовательно, общее решение однородного уравнения имеет вид  , где
, где 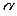 и
и  - соответственно действительная и мнимая части комплексных корней. В данном случае
- соответственно действительная и мнимая части комплексных корней. В данном случае 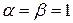 . Таким образом, общее решение исходного уравнения имеет вид:
. Таким образом, общее решение исходного уравнения имеет вид:
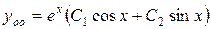 .
.
Чтение учебника
1. Изучая материал по учебнику, следует переходить к следующему вопросу только после правильного понимания предыдущего, производя на бумаге все вычисления (в том числе и те, которые ради краткости опущены в учебнике) и выполняя имеющиеся в учебнике чертежи.
2. Особое внимание следует обращать на определение основных понятий. Студент должен подробно разбирать примеры, которые поясняют такие определения, и уметь строить аналогичные примеры самостоятельно.
3. Необходимо помнить, что каждая теорема состоит из предположений и утверждения. Все предположения должны обязательно использоваться в доказательстве. Нужно добиваться точного представления о том, в каком месте доказательства использовано каждое предположение теоремы. Полезно составлять схемы доказательств сложных теорем. Правильному пониманию многих теорем помогает разбор примеров математических объектов, обладающих и не обладающих свойствами, указанными в предположениях и утверждениях теорем.
4. При изучении материала по учебнику полезно вести конспект, в который рекомендуется вписывать определения, формулировки теорем, формулы, уравнения и т. д. На полях конспекта следует отмечать вопросы, выделенные студентом для получения письменной или устной консультации преподавателя.
5. Письменное оформление работы студента имеет исключительно важное значение. Записи в конспекте должны быть сделаны чисто, аккуратно и расположены в определенном порядке. Хорошее внешнее оформление конспекта по изученному материалу не только приучит студента к необходимому в работе порядку, но и позволит ему избежать многочисленных ошибок, которые происходят из-за небрежных, беспорядочных записей.
6. Выводы, полученные в виде формул, рекомендуется в конспекте подчеркивать или обводить рамкой, чтобы при перечитывании конспекта они выделялись и лучше запоминались. Опыт показывает, что многим студентам помогает в работе составление списка, содержащего важнейшие и наиболее часто употребляемые формулы курса. Такой список не только помогает запомнить формулы, но и может служить постоянным справочником для студента.
Решение задач
1. Чтение учебника должно сопровождаться решением задач, для чего рекомендуется завести специальную тетрадь.
2. При решении задач нужно обосновывать каждый этап решения исходя из теоретических положений курса. Если студент видит несколько путей решения, то он должен сравнить их и выбрать из них самый лучший. Полезно до начала вычислений составить краткий план решения.
3. Решения задач и примеров следует излагать подробно, а вычисления в строгом порядке, отделяя вспомогательные вычисления от основных. Чертежи можно выполнять от руки, но аккуратно и в соответствии с данными условиями. Если чертеж требует особо тщательного выполнения (например, при графической проверке решения, полученного путем вычислений), то следует пользоваться линейкой, транспортиром, лекалом и указывать масштаб.
4. Решение каждой задачи должно доводиться до ответа, требуемого условием, и по возможности с выводом формулы в общем виде. Затем в полученную формулу подставляют числовые значения (если они даны). В промежуточных вычислениях не следует вводить приближенные значения корней, числа p и т. п.
5. Полученный ответ следует проверять способами, вытекающими из существа данной задачи. Если, например, решалась задача с конкретным физическим или геометрическим содержанием, то полезно, прежде всего, проверить размерность полученного ответа. Полезно также, если возможно, решить задачу несколькими способами и сравнить полученные результаты.
6. Решение задач определенного типа нужно продолжать до приобретения устойчивых навыков в их решении.
Самопроверка
1. После изучения определенной темы по учебнику и решения достаточного количества соответствующих задач студенту рекомендуется воспроизвести по памяти определения, выводы формул, формулировки и доказательства теорем. Вопросы для самопроверки, приведенные в настоящем пособии, даны с целью помочь студенту в повторении, закреплении и проверке прочности усвоения изученного материала. В случае необходимости надо еще раз внимательно разобраться в материале учебника, решить ряд задач.
2. Иногда недостаточность усвоения того или иного вопроса выясняется только при изучении дальнейшего материала. В этом случае надо вернуться назад и повторить плохо усвоенный раздел.
3. Важным критерием усвоения теории является умение решать задачи на пройденный материал. Однако здесь следует предостеречь студента от весьма распространенной ошибки, заключающейся в том, что благополучное решение задач воспринимается им как признак усвоения теории. Часто правильное решение задачи получается в результате применения механически заученных формул, без понимания существа дела. Можно сказать, что умение решать задачи является необходимым, но недостаточным признаком хорошего знания теории.
Консультации
1. Если в процессе работы над изучением теоретического материала или при решении задач у студента возникают вопросы, разрешить которые самостоятельно не удается (неясность терминов, формулировок теорем, отдельных задач и др.), то он может обратиться к преподавателю для получения от него письменной или устной консультации.
2. В своих вопросах студент должен точно указать, в чем он испытывает затруднение. Если он не разобрался в теоретических объяснениях, или в доказательстве теоремы, или в выводе формулы по учебнику, то нужно указать, какой это учебник, год его издания и страницу, где рассмотрен затрудняющий его вопрос, и что именно его затрудняет. Если студент испытывает затруднение при решении задачи, то следует указать характер этого затруднения, привести предполагаемый план решения.
3. За консультацией следует обращаться и при сомнении в правильности ответов на вопросы для самопроверки.
Контрольные работы
1. В процессе изучения курса математики студент должен выполнить ряд контрольных работ, главная цель которых – оказать студенту помощь в его работе. Рецензии на эти работы позволяют студенту судить о степени усвоения им соответствующего раздела курса; указывают на имеющиеся у него пробелы в знаниях, на желательное направление дальнейшей работы; помогают сформулировать вопросы для постановки их перед преподавателем.
2. Не следует приступать к выполнению контрольного задания, не решив достаточного количества задач по материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания вызывается тем, что студент не выполнил это требование.
3. Контрольные работы должны выполняться самостоятельно. Несамостоятельно выполненная работа не дает возможности преподавателю-рецензенту указать студенту на недостатки в его работе, в усвоении им учебного материала, в результате чего студент не приобретает необходимых знаний и может оказаться неподготовленным к устному зачету и экзамену.
4. Не рекомендуется присылать в академию одновременно работы по нескольким заданиям: это не дает возможности рецензенту своевременно указать студенту на допущенные им ошибки и удлиняет срок рецензирования работ.
5. Прорецензированные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять. Без предъявления прорецензированных работ студент не допускается к сдаче зачета и экзамена.
Лекции, практические занятия.
Во время установочных сессий для студентов-заочников организуются лекции и практические занятия. Они носят, как правило, обзорный характер. Их цель обратить внимание на общую схему построения соответствующего раздела курса, подчеркнуть важнейшие места, указать главные практические приложения теоретического материала, привести факты из истории науки. Кроме того, на этих занятиях могут быть более подробно рассмотрены отдельные вопросы программы, отсутствующие или недостаточно полно освещенные в рекомендуемых пособиях.
Для студентов ускоренной формы обучения лекции и практические занятия проводятся в течение всего учебного года и носят более систематический характер, однако и они призваны оказать только лишь помощь студенту в его самостоятельной работе.
Зачеты и экзамены
На экзаменах и зачетах выясняется, прежде всего, отчетливое усвоение всех теоретических и практических вопросов программы и умение применять полученные знания к решению практических задач. Определения, теоремы, правила должны формулироваться точно и с пониманием существа дела; решение задач в простейших случаях должно выполняться без ошибок и уверенно; всякая письменная и графическая работа должна быть сделана аккуратно и четко. Только при выполнении этих условий знания могут быть признаны удовлетворяющими требованиям, предъявляемым программой.
При подготовке к экзамену учебный материал рекомендуется повторить по учебнику и конспекту.
Вопросы для самопроверки
Дата: 2018-11-18, просмотров: 384.