Студент должен знать понятия: событие, частота и вероятность появления события, совместные и несовместные события, теоремы сложения и умножения вероятностей.
Уметь находить вероятность в простейших задачах, используя классическое определение вероятности, решение задач с применением теоремы сложения вероятностей для несовместных событиях.
Под испытанием понимают реализацию данного комплекса условий, в результате которого непременно произойдет какое-либо событие. Например, бросание монеты – это испытание, выпадение цифры или герба – событие.
Событием называется событие, связанное с данным испытанием, которое при осуществлении испытания может произойти, а может не произойти. Например: выстрел по цели – это опыт, случайные события в этом опыте - попадание в цель или промах.
Событие в данных условиях называется достоверным, если в результате опыта оно непременно произойдет, и невозможным, если оно заведомо не произойдет. Например, выпадение не более шести очков при бросании игральной кости – достоверное событие, выпадение 7 очков при бросании одной игральной кости – невозможное событие.
Событие называется несовместными, если никакие два из них могут появиться вместе. Например, попадание и промах, при одном выстреле – это несовместные события.
События называются равновозможными, если одно из них не является объективно более возможным, чем другие. Например, при бросании монеты выпадение герба или числа – события равновозможные.
Говорят, что несколько событий в данном опыте образуют полную систему событий, если в в результате опыта непременно должно произойти хотя бы одно из них. Например, при бросании игральной кости события, состоящее в выпадении одного, двух, трех, четырех, пяти и шести очков, образуют полную систему событий. Пусть А – случайное событие, связанное с некоторым опытом. Повторим опыт n раз в одних и тех же условиях и пусть при этом событие А появилось m раз. Отношение  называется частотой события А. При многократном повторении опыта частота события принимает значения, близкие к некоторому постоянному числу. Числовая мера степени объективной возможности события - это вероятность события. Вероятность события А обозначается Р(А).
называется частотой события А. При многократном повторении опыта частота события принимает значения, близкие к некоторому постоянному числу. Числовая мера степени объективной возможности события - это вероятность события. Вероятность события А обозначается Р(А).
Пусть из системы n несовместных равновозможных исходов испытания m исходов благоприятствуют событию А. Тогда вероятностью события А называют отношение m числа исходов, благоприятствующих событию А к числу все исходов данного испытания: Р(А) =  . Если А – случайное событие, m
. Если А – случайное событие, m 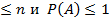
Эта формула носит название классического определение вероятности. Если В – достоверное событие ( невозможное) , то 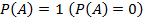 . Таким образом, вероятность события заключается в следующих пределах:
. Таким образом, вероятность события заключается в следующих пределах: 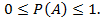
Независимость случайных событий. Событие В называется независимым от события А, если появление события А не изменит вероятности события В. Если событие В не зависит от события А , то и событие А не зависит от события В; это означает, что свойство независимости взаимно. Несколько событий называется попарно независимыми, если каждые два события независимы.
Суммой А + В двух событий А и В называется событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А – попадание при первом выстреле, В - попадание при втором выстреле, то А + В – попадание при первом выстреле, или при втором, или при обоих выстрелах. Если события А и В – несовместные, то А + В – событие, состоящее в появлении одного из этих событий, безразлично какого.
Теорема: Вероятность появления одного из двух несовместных событий, равна сумме вероятностей этих событий: Р (А + В) = Р (А) + Р (В)
Произведением двух событий А и В называется событие АВ, состоящее в совместном появлении этих событий. Например, если А – деталь годная, а В – деталь окрашенная, то АВ – деталь годная и окрашенная.
Условной вероятностью 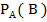 называется вероятность события В, вычисленную в предположении, что событие А уже наступило. Условная вероятность события В при условии, что событие А уже наступило, по определению равна:
называется вероятность события В, вычисленную в предположении, что событие А уже наступило. Условная вероятность события В при условии, что событие А уже наступило, по определению равна: 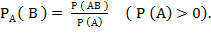
Теорема: Вероятность совместного появления двух событий, равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предложении, что первое событие наступило: 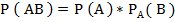
Примеры.
1. В ящике имеется 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.
Решение: Р = 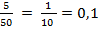
2. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого, наудачу извлеченного жетона , не содержит цифры 5.
Решение: Из чисел от 1 до 100 девятнадцать чисел содержат цифру 5, не содержит – 81 число. Тогда Р = 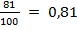
3. В урне 30 шаров: 10 красных, 5 сини, 15 белы. Найти вероятность появления цветного шара ( красного или синего).
Решение: Вероятность появления красного шара: Р = 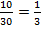
Вероятность появления синего шара: Р = 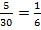
События А и В несовместны, по теореме сложения:
Р (А + В) = Р (А) + Р (В)= 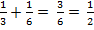
4. У сборщика имеется 3 конусных и 7 эллиптических валиков. Сборщик взял один валик, а затем второй. Найти вероятность того, что первый из взятых валиков конусный, а второй эллиптический.
Решение: Вероятность, что первый валик – конусный: : Р = 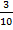 . Вероятность того, что второй валик окажется эллиптическим, считая что первый валик – конусный, т е условная вероятность:
. Вероятность того, что второй валик окажется эллиптическим, считая что первый валик – конусный, т е условная вероятность: 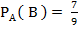 . По теореме умножения, искомая вероятность:
. По теореме умножения, искомая вероятность: 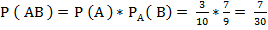
6.4 Векторы и координаты
Студент должен знать: определение вектора, равных, компланарных ,коллинеарных векторов, длины вектора, координат вектора, скалярного произведения векторов и свойств скалярного произведения векторов. Формулы для нахождения координат, длины вектора, середины отрезка и расстояния между двумя точками, скалярного произведения в координатах.
Уметь решать геометрические задачи с помощью использования формул для нахождения координат, длины вектора, середины отрезка и расстояния между двумя точками, скалярного произведения в координатах и свойств скалярного произведения.
Вектор – направленный отрезок. Длиной (модулем) ненулевого вектора называется длина отрезка AB. Длина нулевого вектора равна нулю.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора АВ и С Д коллинеарны, а лучи AB и CD сонаправлены, то векторы и называются сонаправленными. Этот факт обозначается так: ↑↑. Если же эти лучи не являются сонаправленными, то векторы и называются противонаправленными. Этот факт обозначается так: ↑↓.
Два вектора называются равными, если они сонаправлены и их длины равны.
Векторы называются компланарными, если имеются равные им вектора, параллельные одной плоскости. Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси. Единичный вектор, направленный вдоль оси x, обозначается I, единичный вектор, направленный вдоль оси y –j, вдоль оси z – k. Вектора I, j, k называются координатными векторами. По своему построению эти векторы некомпланарны, а значит, любой вектор a можно разложить по координатным векторам:
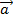 = x
= x 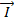 + y
+ y 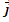 + z
+ z 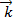 . Кроме того, отметим, что коэффициенты разложения определяются единственным образом. Эти коэффициенты и называются координатами вектора в данной системе координат.
. Кроме того, отметим, что коэффициенты разложения определяются единственным образом. Эти коэффициенты и называются координатами вектора в данной системе координат.
Дата: 2018-11-18, просмотров: 660.