1. Найти область определения функции.
2. Исследовать четность и периодичность функции.
3. Исследовать критические точки и точки разрыва.
4. Найти точки пересечения графика с осями координат.
5. Определить точки экстремума, интервалы возрастания и убывания функции. y′
6. Определить точки перегиба графика, интервалы его выпуклости и вогнутости. y′′
7. Построить график функции.
Пример: Исследовать функцию у = - 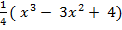 и построить график.
и построить график.
Решение.
1) Область определения функции – вся числовая прямая, то есть D( y) = (−∞;+∞) .
Точек разрыва нет
2) Точки пересечения с осями координат: у = - 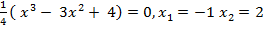
X = 0, y = - 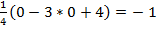
3) Функция общего вида, так как у = - 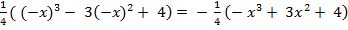
4) Экстремумы и монотонность. Вычисляем первую производную:
у| = - 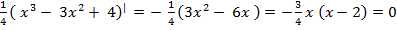
Находим критические точки: x = 0, x = 2 . Исследуем знак производной на интервалах,
на которые критическая точка делит область определения функции.
5)Строим таблицу
| х | - | 0 | 2 | ||
| f| | - | 0 | + | 0 | - |
| f | ↘ | - 1 | ↗ | 0 | ↘ |
5) Выпуклость и точки перегиба. Вычисляем вторую производную.
У| | = 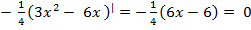 x = 1
x = 1
+ -
1
Функция выпукла вверх на интервале (1;+∞) , выпукла вниз на интервале (−∞;1) . Точка
перегиба: x =1, y(1) = −0,5 .
6) Строим график функции, отметим ключевые точки:
Алгоритм нахождения наибольшего и наименьшего значения функции y = f ( x ) на отрезке [ a , b ]
1) Найти производную функции;
2) Найти стационарные и критические точки, лежащие внутри отрезка [a,b];
3) Вычислить значение функции y=f(x) в точках, отобранных на втором шаге, в точках a и b, выбрать среди них наибольшее и наименьшее значение функции
Пример: Найти наибольшее и наименьшее значение функции y=x2 - 8x+19 на
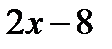
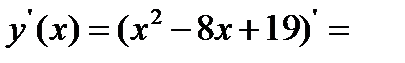 [-1,5]
[-1,5]
1)
2) 2x - 8=0
2x = 8
X = 4
У = 52 – 8*5 + 19 = 4 при х = 5
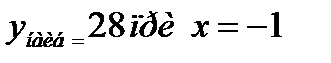 3)
3)
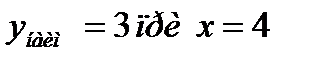 4)
4)
Интегральное исчисление.
Студент должен знать: определение первообразной функции, определенного и неопределенного интеграла, правила интегрирования, основные способы нахождения интегралов, таблицу интегралов, формулу Ньютона - Лейбница.
Уметь находить первообразную функции, применять правила интегрирования и таблицу интегралов при решении интегралов, применять формулу Ньютона – Лейбница при решении определенного интеграла, находить площадь криволинейной трапеции с помощью определенного интеграла.
Функция F(x) называется первообразной для функции f(x) на некотором промежутке, если для всех x из этого промежутка выполняется равенство
F |(x) = f (x).
Множество всех первообразных F (x) + c для функции f(x) называется неопределённым интегралом от функции f(x) и обозначается символом 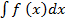 . Таким образом, по определению:
. Таким образом, по определению: 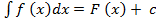
, где c – const.
Функция f (x) называется подынтегральной функцией, f (x) dx – подынтегральным выражением, а сам процесс отыскания множества первообразных F (x) + c – интегрированием. Интегрирование – это восстановление функции по её производной (обратное действие по отношению к дифференцированию).
Достаточное условие интегрируемости: если на некотором промежутке функция непрерывна, то она интегрируема на нём.
Дата: 2018-11-18, просмотров: 624.