Показательные уравнения — уравнения, в которых неизвестное содержится в показателе степени.
Решение показательных уравнений часто сводится к решению уравнения вида ax = a b, где a > 0, a ≠ 1, x — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием a > 0, a ≠ 1 равны только тогда, когда равны их показатели.
Показательными называются неравенства, в которых неизвестная переменная содержится только в показателях каких-либо степеней.
Для решения показательных неравенств требуется знание следующей теоремы:
Теорема. Если a > 1, то неравенство af(x) > ag(x) равносильно неравенству того же смысла: f(x) > g(x). Если 0 < a < 1, то показательное неравенство af(x) > ag(x) равносильно неравенству противоположного смысла: f(x) < g(x).
Примеры: 1. Решите уравнение: 3 4x-5 = 3x+4 .
Решение. 3 4x-5 = 3x+4
4x - 5 = x+4
3x=9
x = 3 Ответ:3
3. Решите неравенство : 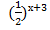 >
> 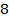
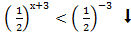
Х + 3 < - 3
Х< - 6
Ответ: х ε ( - ∞; -6 )
Логарифмическое уравнение – это уравнение вида
loga b(x) = loga c(x), где а > 0, a ≠ 1.
Уравнения, сводящиеся к этому виду, также называются логарифмическими уравнениями.
Логарифмическое неравенство – это неравенство вида
loga b(x) > loga c(x), где а > 0, a ≠ 1.
Неравенства, сводящиеся к этому виду, также называются логарифмическими неравенствами.
Для решения логарифмических неравенств loga b(x) > loga c(x) обычно применяют систему неравенств следующего вида:
| При a > 1: │ b(x) > 0, │ c(x) > 0, │ b(x) > c(x) | При 0 < a < 1: │ b(x) > 0 │ c(x) > 0 │ b(x) < c(x). |
Примеры: 1. log3 (x2 – 3x – 5) = log3 (7 – 2x).
Решение.
x2 – 3x – 5 = 7 – 2x
x2 – 3x – 5 – 7 + 2x = 0
x2 – x – 12 = 0
Решив квадратное уравнение, находим его корни:
x1 = 4, x2 = –3.
Проверим, при каком из двух значений х уравнение имеет смысл.
Мы уже знаем, что логарифмическое уравнение равносильно уравнению b(x) = c(x) только в том случае, если b(x) > 0 и c(x) > 0. Следовательно, выводим два неравенства:
x2 – 3x – 5 > 0,
7 – 2x > 0.
При х = 4 неравенства неверны. Значит, 4 не является решением уравнения.
При х = –3 неравенства верны. Значит, 3 является единственным решением уравнения.
Ответ: 3
2. log3 (2x – 4) > log3 (14 – x).↑
Решение.
1) В основании обеих частей уравнения – одно и то же число 3. Значит, можем убрать значки логарифмов. Поскольку 3 больше 1, то, следуя правилу, составляем следующую систему неравенств:
│ 2x – 4 > 0
│14 – x > 0
│2x – 4 > 14 – x.
Решаем неравенства и получаем:
│x > 2
│x < 14
│x > 6
ответ: 6 < x < 14.
4.4 Основные тригонометрические формулы. .
Студент должен знать: тригонометрические формулы, определение простейших тригонометрических уравнений, формулы для решения простейших тригонометрических уравнений.
Уметь решать тригонометрические уравнения, пользоваться таблицей значений тригонометрических функций .
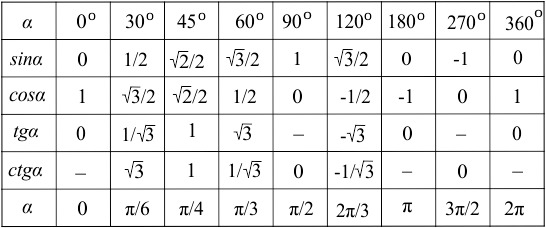
Соотношения между тригонометрическими функциями одного аргумента 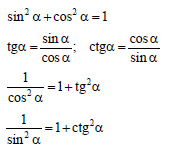
Дата: 2018-11-18, просмотров: 712.