Аннотация
Методическая разработка для самоподготовки студентов заочного отделения по дисциплине: «математика», имеющих основное образование. Указания ставят своей целью оказать помощь студентам заочной формы обучения для организации самостоятельной работы по овладению системы знаний, умений и навыков в объеме действующей программы, в количестве 66 часов. Методические указания для студентов содержит 11 разделов, в соответствии с основными темами программы, в которых приведены основные понятия и формулы курса, а также методы и примеры решения ключевых примеров и задач. Весь курс разделен на 2 части по количеству контрольных работ, которые необходимо решить студентам. Задания контрольных работ приведены после теоретической части
Рецензия (внешняя и внутренняя).
Рецензия
на методичесую разработку по дисциплине «Математика»
для студентов заочного отделения
МБПОУ «Псковский агротехнический колледжа»
Методическая разработка учебной дисциплины «Математика» на базе основного общего образования является единой для всех форм обучения. Учебная дисциплина «Математика» является образовательной учебной дисциплиной в цикле математических и общих естественных дисциплин, которая обеспечивает общеобразовательный уровень подготовки специалиста. Программа по дисциплине «Математика» разработана на основе Федерального государственного образовательного стандарта по специальностям среднего профессионального образования
В программе отмечено, что с целью овладения указанным видом профессиональной деятельности и соответствующими общими компетенциями обучающийся в ходе освоения дисциплины «Математика» должен:
уметь:
· выполнять действия и иметь практический опыт: измерений, вычислений, расчетов, применения формул математического аппарата к выполнению практических работ и самостоятельных работ.
- знать и уметь использовать математические методы при решении прикладных задач;
· решать прикладные задачи в области профессиональной деятельности;
Знать:
· основные математические методы решения прикладных задач в области профессиональной деятельности;
· основные понятия и методы алгебры и начала математического анализа, геометрии.
· основы интегрального и дифференциального исчисления.
Содержание программы рассчитано на 66 аудиторных часов.
В теме «Действительные числа. Приближенные вычисления и вычислительные средства» особое внимание уделено совершенствованию таких навыков, как: а) округление чисел с заданной точностью; б) выполнение вычислений без точного учета погрешностей; в) оценка точности приближений по количеству значащих цифр. Для усиления практической направленности повторения приближенных вычислений рассматриваются параллельно с изучением работы на микрокалькуляторе.
Решение уравнений, неравенств, их систем пронизывает весь курс дисциплины. В начале курса систематизируются знания и умения студентов по решению простейших уравнений, неравенств и их систем с одной и двумя переменными. Далее, класс рассматриваемых уравнений и неравенств расширяется за счет расширения запаса изученных функций (показательные, логарифмические, тригонометрические). Для решения систем с большим числом неизвестных используются определители. В технической механике, в электротехнике, в экономических дисциплинах используются системы линейных уравнений не только с двумя и тремя неизвестными. Поэтому формирование навыков решения систем линейных уравнений является важной задачей изучения темы «Определители».
Основной целью изучения раздела «Последовательности и функции» является развитие графической культуры студентов, т.к. умение читать графики часто требуется в практических задачах.
Прикладную направленность имеет и раздел «Дифференциальное исчисление». Везде, где требуется охарактеризовать скорость протекания некоторого процесса, т.е. скорость изменения одной величины относительно другой, используется понятие производной. Построение графиков с помощью производной является иллюстрацией эффективности методов дифференциального исчисления.
Значимость раздела «Интегральное исчисление» связана с применением понятия интеграла для моделирования многих важных процессов. Речь идет о «суммировании» бесконечно малых элементов, восстановлении функции по ее производной и начальным условиям.
Всестороннее использование векторного аппарата предполагают физика, техническая механика, электротехника. Раздел «Векторы и координаты» из-за многообразия связей указанной темы с общетехническими и специальными дисциплинами изучается одновременно для случая плоскости и пространства. Формирование пространственного воображения необходимо для студентов технических специальностей. Изложение материала раздела «Геометрические тела и их поверхности» характеризуется постоянным обращением к наглядности, опыту студентов, использованием рисунков и чертежей на всех этапах обучения и развитием геометрической интуиции на этой основе.
В процессе изучения дисциплины «Математика» студенты должны написать 2 контрольных работы и по окончанию курса дисциплины устный экзамен.
Программа по дисциплине «Математика» преподавателя Чернопийской
соответствует требованиям, предъявляемым к разработке методических указаний и может быть использована для подготовки выпускников средних профессиональных заведений.
Оглавление.
1. Общие методические указания. 5
2. Примерный тематический план. 6
3. Учебное задание. 9
Часть 1.
4.1 Действительные числа. 9
4.2 Последовательности и функции. 11
4.3 Показательные и логарифмические уравнения. 14
4.4 Основные тригонометрические формулы. 17
4.5 Тригонометрические уравнения. 18
5 Контрольные задания. 20
6 Учебное задание. 23
Часть 2.
6.1 Дифференциальное исчисление. 23
6.2 Интегральное исчисление. 27
6.3 Комбинаторика, статистика, теория вероятностей. 31
6.4 Векторы и координаты. 33
6.5 Объемы и площади поверхностей геометрических тел. 34
7 Контрольные задания. 36
8 Литература. 41
Введение
ЧАСТЬ 1
Действительные числа
Методические указания.
Студент должен знать: определения линейного и квадратного уравнения, формулы дискриминанта и корней квадратного уравнения, определение определителей второго и третьего порядка, формулировки теоремы Виета и теоремы Крамера.
Уметь решать линейные, квадратные уравнения и неравенства, Иррациональные уравнения, системы линейных уравнений, используя теорему Крамера.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Квадратные уравнения могут иметь два различных корня, один корень и не иметь корней.
Чтобы определить, сколько корней имеет уравнение надо найти дискриминант — это просто число D = b2 − 4ac.
Если D < 0, корней нет;
Если D = 0, есть один корень;
Если D > 0, корней будет два.
Если дискриминант D > 0, корни можно найти по формулам: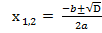 
Квадратные неравенства можно решать двумя способами. Один способ - это метод интервалов. Другой способ: схематичный рисунок.
Определители второго и третьего порядка. Выражение
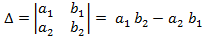называется определителем второго порядка.
Выражение
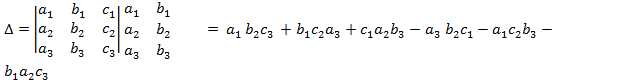называется определителем третьего порядка.
Теорема Крамера . Если определитель Δ системы линейных алгебраических уравнений с n неизвестными отличен от нуля, то эта система имеет единственное решение, которое находится по формулам Крамера: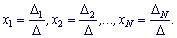 
Примеры: Решить с помощью метода Крамера систему уравнений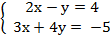 
Решение: Δ =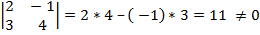 
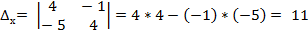
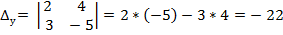
Х =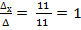 
У = 
= 
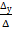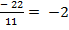
Ответ: (1; - 2 )
Теоремы о пределах.
1. Предел константы равен самой этой константе: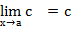 
2. Постоянный множитель можно выносить за знак предела:
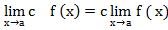
3. Предел суммы (разности) функций равен сумме (разности) пределов этих функций:
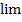[ f (х) ± g (х)] = 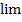f (х) ± 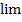g (x).
4. Предел произведения функций равен произведению пределов этих функций:
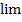[ f (х) • g (х)] = 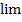f (х) • 
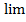g (x).
5. Предел отношения двух функций равен отношению пределов этих функций, если только предел делителя не равен нулю:
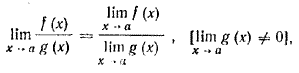
Замечательные пределы.
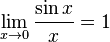
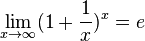
Где е – число иррациональное, е приблизительно равняется 2,71828…
Методы нахождения пределов.
1. Простая подстановка значения аргумента . Если при простой подстановке иполучаются неопределенности вида 
или 
, то используются способы 2 и 3.
2. Числитель и знаменатель делятся на х с наибольшим показателем степени.
3. Дробь раскладывается на множители .
4. Используются замечательные пределы.
Примеры:
1. 
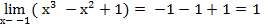
2. 
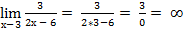
3. 
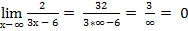
4. 
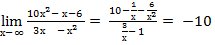
5. 
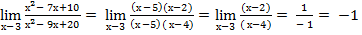
6. 
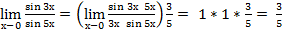
7. 
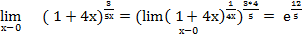
Свойства логарифма.
1. 
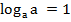
2. 
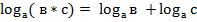
3. 
( 
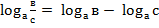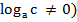
4. 
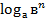= n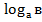 
( 
)
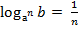
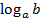5. 
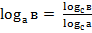- переход к новому основанию
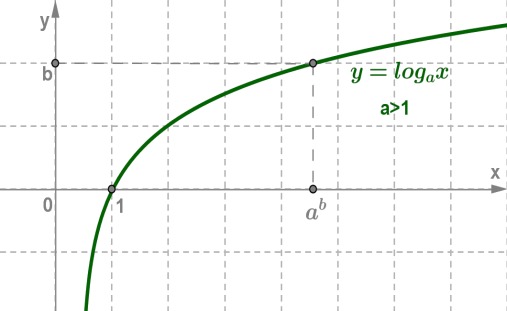
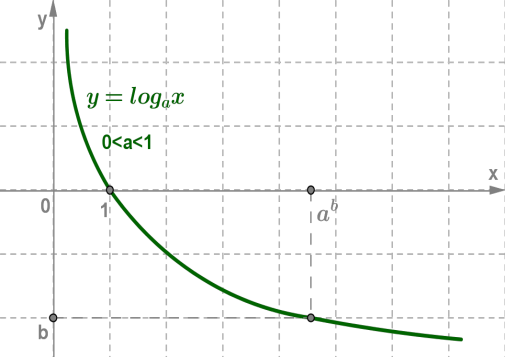
Функция вида y = ax, где a больше нуля и а не равно единице называется показательной функцией.
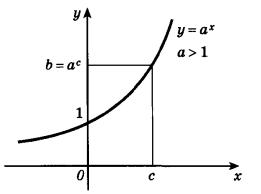
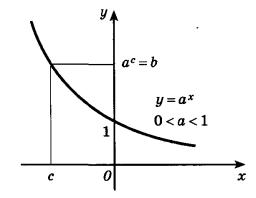
Основные свойства степеней:
ax*ay = a(x + y);
(ax) : (ay) = a(x-y);
(a*b)x = (ax)*(ay);
(a/b)x = ax/bx;
(ax)y = a(x * y).
Функцию, заданную формулой y=logax, называют логарифмической функцией с основанием a.
(a>0,a≠1)
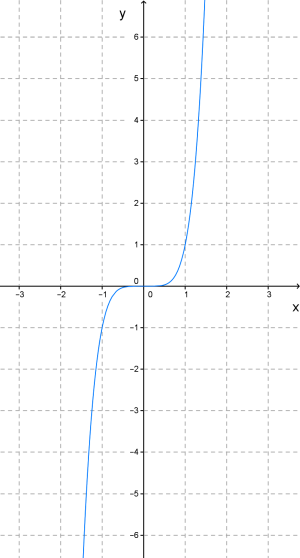
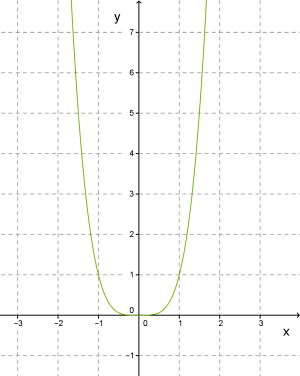
Степенной функцией называют функции вида у = хr, где r-любое действительное число.
r – четное число r – нечетное
Правила дифференцирования.
Вынесение числового множителя: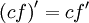 
Сумма :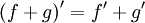 
Произведение :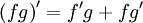 
Частное :
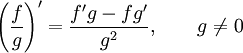
Примеры:
1) у/ (х) = (х3 + 2 х2 – 3х + 5)/ = 3х2 + 4 х – 3
2) у/ (х)= (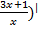 
= 
= 
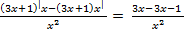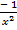
3) y|(x) =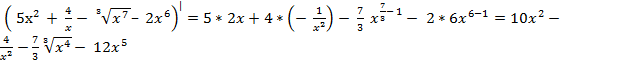 
4) y|(x) = (( 5x – 3) * 2x)| =( 5x – 3)| *( 2x) + ( 5x – 3) * (2x)|=( 5*1 – 0) 2x +( 5x – 3)* 2x*Ln 2 =
= 5*2x+( 5x – 3) 2xLn 2
Функция у = f(x) называется непрерывной при заданном значении х,если она определена в некоторой окрестности этой точки и если бесконечно малому приращению х соответствует бесконечно малое приращение у.
Функция у = f(x) монотонно возрастает, если большему значению аргумента х соответствует большее значение функции. Условие возрастания: у/ (х) > 0.
Функция у = f(x) монотонно убывает, если большему значению аргумента х соответствует меньшее значение функции. Условие убывания: у/ (х) < 0.
Функция у = f(x) имеет максимум ( минимум) при х = а f /(x) = 0 , если при всех х, близких к а знак производной меняется с + на – ( с – на +).
Интегральное исчисление.
Студент должен знать: определение первообразной функции, определенного и неопределенного интеграла, правила интегрирования, основные способы нахождения интегралов, таблицу интегралов, формулу Ньютона - Лейбница.
Уметь находить первообразную функции, применять правила интегрирования и таблицу интегралов при решении интегралов, применять формулу Ньютона – Лейбница при решении определенного интеграла, находить площадь криволинейной трапеции с помощью определенного интеграла.
Функция F(x) называется первообразной для функции f(x) на некотором промежутке, если для всех x из этого промежутка выполняется равенство
F |(x) = f (x).
Множество всех первообразных F (x) + c для функции f(x) называется неопределённым интегралом от функции f(x) и обозначается символом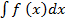 
. Таким образом, по определению: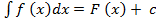 
, где c – const.
Функция f (x) называется подынтегральной функцией, f (x) dx – подынтегральным выражением, а сам процесс отыскания множества первообразных F (x) + c – интегрированием. Интегрирование – это восстановление функции по её производной (обратное действие по отношению к дифференцированию).
Достаточное условие интегрируемости: если на некотором промежутке функция непрерывна, то она интегрируема на нём.
Интегрирование по частям.
Метод интегрирования по частям решает очень важную задачу, он позволяет интегрировать некоторые функции, отсутствующие в таблице, произведение функций, а в ряде случаев – и частное.
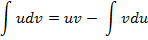
- Пример 1
- 
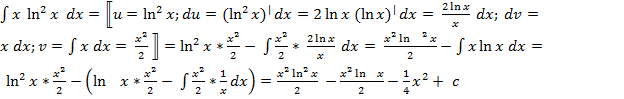
Определенный интеграл.
Пусть функция y = f (x) определена на промежутке [ a; b ]. Для определённости и простоты считаем, что функция положительна и непрерывна на данном отрезке. Поставим задачу найти площадь криволинейной трапеции, ограниченной графиком функции y = f (x) , прямыми x = a, x = b и осью OX .
Разобьём отрезок [ a; b] на n частей следующими точками: a = x0< x1 < x2 < … < xn = b
(красные точки):
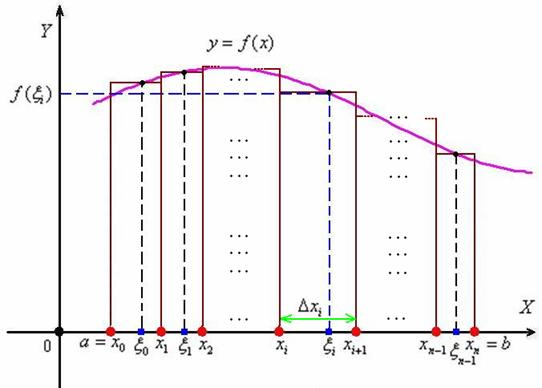
В результате получено n частичных промежутков[ x0; x1] [ x1; x2] … [ xn -1; xn] с длинами ∆x0, ∆x1, …, ∆xn соответственно. Рассмотрим i промежуток[ xi; xi+1] . Его длина, очевидно, равна ∆x i . Значению аргумента ξ i соответствует значение
f (ξ i) функции, и произведение ∆x i f (ξ i) в точности равно площади соответствующего прямоугольника. Аналогично устроен каждый отрезок. Составим сумму, которая равна площади ступенчатой фигуры и называется интегральной суммой, и её часто записывают в свёрнутом виде:
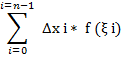
Длина любого промежуточного отрезка становится бесконечно малой.
Конечный предел интегральной суммы
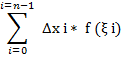
при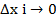 
, не зависящий ни от способа дробления отрезка, ни от выбора точек, называется определённым интегралом функции по промежутку [ a; b] и обозначается символом 
.
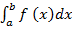формула Ньютона-Лейбница:
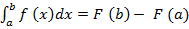, где – F (x) первообразная функция для функции
f (x).
Таблица интегралов.
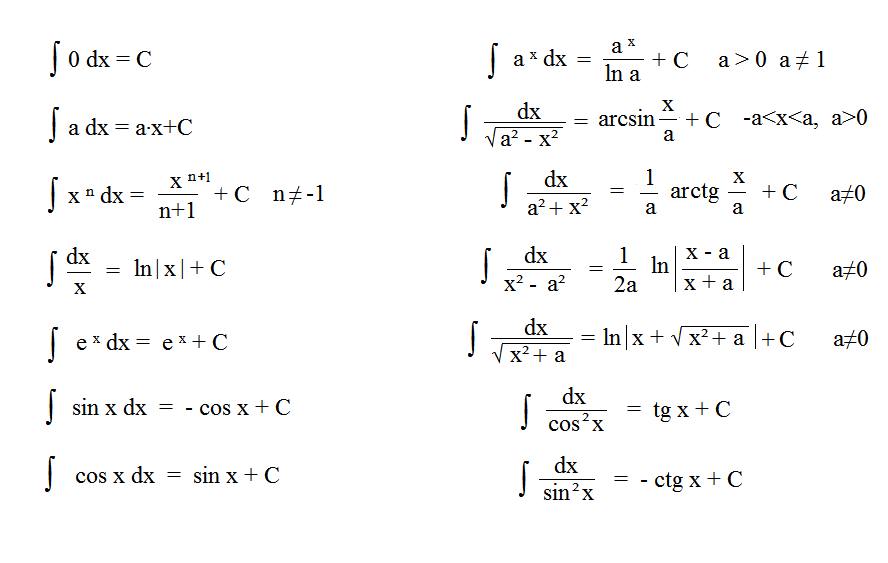
Пример1:
Найти путь, пройдённый телом в промежуток времени от t1 =2c до t2 = 5c , если известен закон изменения его скорости v = t2 + 2 (м/с)
X =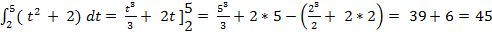 
Пример 2:
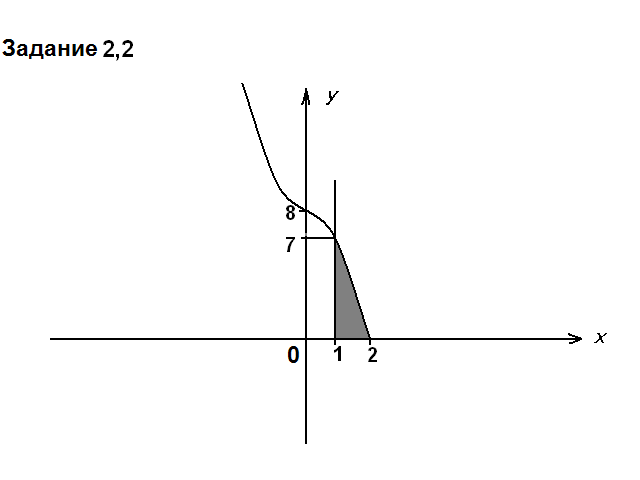
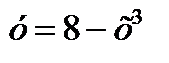Вычислить площадь фигуры, ограниченной осью ох, прямой х=1 и графиком функции
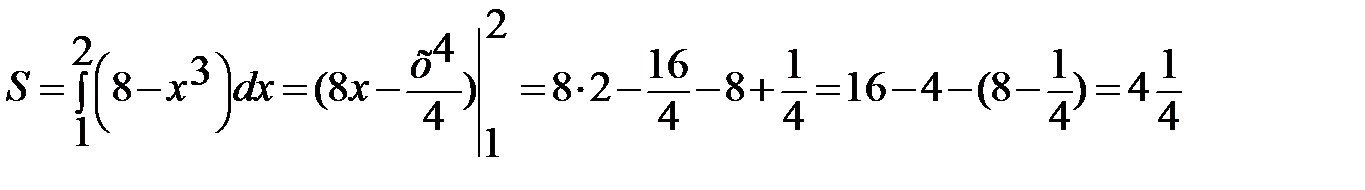
Заключение
(кратко обобщается основная идея содержания, раскрываются практически значимые следствия, предполагаемые результаты из общего содержания работы. Здесь же автор должен показать возможные пути дальнейшего совершенствования и развития изложенных педагогических решений, методических рекомендаций).
Рекомендуемая литература.
Основная:
Л1. Л.Н. Колмогоров. Алгебра и начала анализа, 10-11 класс – М.: Просвещение,2010.
Л2. Богомолов Н.В. Практические занятия по математике, учебное пособие для техникумов. – М.: Высшая школа, 2009.
Л3.Атанасян Л.С. Геометрия 10-11- М.: Просвещение, 2011
Л.4. Филимонова Е.В. «Математика для средних специальных учебных заведений: учебное пособие, - Изд.4-ое, Ростов н /Д: Феникс
Дополнительная:
ДЛ1. Алгебра и начала анализа. Часть 1 и 2. Под редакцией Г.Н. Яковлева – М.: Наука, 1987.
ДЛ2. Геометрия. Под редакцией Г.Н. Яковлева – М.: Наука, 1988(89).
ДЛ3. Н.Г. Федин, С.Н. Федин. Геометрия – М.: Высшая школа, 1989
Аннотация
Методическая разработка для самоподготовки студентов заочного отделения по дисциплине: «математика», имеющих основное образование. Указания ставят своей целью оказать помощь студентам заочной формы обучения для организации самостоятельной работы по овладению системы знаний, умений и навыков в объеме действующей программы, в количестве 66 часов. Методические указания для студентов содержит 11 разделов, в соответствии с основными темами программы, в которых приведены основные понятия и формулы курса, а также методы и примеры решения ключевых примеров и задач. Весь курс разделен на 2 части по количеству контрольных работ, которые необходимо решить студентам. Задания контрольных работ приведены после теоретической части
Рецензия (внешняя и внутренняя).
Рецензия
на методичесую разработку по дисциплине «Математика»
для студентов заочного отделения
МБПОУ «Псковский агротехнический колледжа»
Методическая разработка учебной дисциплины «Математика» на базе основного общего образования является единой для всех форм обучения. Учебная дисциплина «Математика» является образовательной учебной дисциплиной в цикле математических и общих естественных дисциплин, которая обеспечивает общеобразовательный уровень подготовки специалиста. Программа по дисциплине «Математика» разработана на основе Федерального государственного образовательного стандарта по специальностям среднего профессионального образования
В программе отмечено, что с целью овладения указанным видом профессиональной деятельности и соответствующими общими компетенциями обучающийся в ходе освоения дисциплины «Математика» должен:
уметь:
· выполнять действия и иметь практический опыт: измерений, вычислений, расчетов, применения формул математического аппарата к выполнению практических работ и самостоятельных работ.
- знать и уметь использовать математические методы при решении прикладных задач;
· решать прикладные задачи в области профессиональной деятельности;
Знать:
· основные математические методы решения прикладных задач в области профессиональной деятельности;
· основные понятия и методы алгебры и начала математического анализа, геометрии.
· основы интегрального и дифференциального исчисления.
Содержание программы рассчитано на 66 аудиторных часов.
В теме «Действительные числа. Приближенные вычисления и вычислительные средства» особое внимание уделено совершенствованию таких навыков, как: а) округление чисел с заданной точностью; б) выполнение вычислений без точного учета погрешностей; в) оценка точности приближений по количеству значащих цифр. Для усиления практической направленности повторения приближенных вычислений рассматриваются параллельно с изучением работы на микрокалькуляторе.
Решение уравнений, неравенств, их систем пронизывает весь курс дисциплины. В начале курса систематизируются знания и умения студентов по решению простейших уравнений, неравенств и их систем с одной и двумя переменными. Далее, класс рассматриваемых уравнений и неравенств расширяется за счет расширения запаса изученных функций (показательные, логарифмические, тригонометрические). Для решения систем с большим числом неизвестных используются определители. В технической механике, в электротехнике, в экономических дисциплинах используются системы линейных уравнений не только с двумя и тремя неизвестными. Поэтому формирование навыков решения систем линейных уравнений является важной задачей изучения темы «Определители».
Основной целью изучения раздела «Последовательности и функции» является развитие графической культуры студентов, т.к. умение читать графики часто требуется в практических задачах.
Прикладную направленность имеет и раздел «Дифференциальное исчисление». Везде, где требуется охарактеризовать скорость протекания некоторого процесса, т.е. скорость изменения одной величины относительно другой, используется понятие производной. Построение графиков с помощью производной является иллюстрацией эффективности методов дифференциального исчисления.
Значимость раздела «Интегральное исчисление» связана с применением понятия интеграла для моделирования многих важных процессов. Речь идет о «суммировании» бесконечно малых элементов, восстановлении функции по ее производной и начальным условиям.
Всестороннее использование векторного аппарата предполагают физика, техническая механика, электротехника. Раздел «Векторы и координаты» из-за многообразия связей указанной темы с общетехническими и специальными дисциплинами изучается одновременно для случая плоскости и пространства. Формирование пространственного воображения необходимо для студентов технических специальностей. Изложение материала раздела «Геометрические тела и их поверхности» характеризуется постоянным обращением к наглядности, опыту студентов, использованием рисунков и чертежей на всех этапах обучения и развитием геометрической интуиции на этой основе.
В процессе изучения дисциплины «Математика» студенты должны написать 2 контрольных работы и по окончанию курса дисциплины устный экзамен.
Программа по дисциплине «Математика» преподавателя Чернопийской
соответствует требованиям, предъявляемым к разработке методических указаний и может быть использована для подготовки выпускников средних профессиональных заведений.
Оглавление.
1. Общие методические указания. 5
2. Примерный тематический план. 6
3. Учебное задание. 9
Часть 1.
4.1 Действительные числа. 9
4.2 Последовательности и функции. 11
4.3 Показательные и логарифмические уравнения. 14
4.4 Основные тригонометрические формулы. 17
4.5 Тригонометрические уравнения. 18
5 Контрольные задания. 20
6 Учебное задание. 23
Часть 2.
6.1 Дифференциальное исчисление. 23
6.2 Интегральное исчисление. 27
6.3 Комбинаторика, статистика, теория вероятностей. 31
6.4 Векторы и координаты. 33
6.5 Объемы и площади поверхностей геометрических тел. 34
7 Контрольные задания. 36
8 Литература. 41
Введение
Общие методические указания.
Математика – одна из самых важных фундаментальных наук. Методы математического моделирования применяются в традиционных науках, в том числе механике, биологии, экономике, физике и т д . Математические методы необходимы также в решении конкретны задач , которые приходиться решать в ежедневной деятельности технически специальностей, технологов сельхоз производства. Учебная дисциплина «Математика» является естественнонаучной, формирующей базовые знания для освоения общепрофессиональных и специальных дисциплин. Изучение математики для современного специалиста способствует формированию современного научного мышления, обогащению культуры труда и приобщению к вычислительной технике, техническим средствам.
Методические указания ставят своей целью оказать помощь студентам заочной формы обучения для организации самостоятельной работы по овладению системы знаний, умений и навыков в объеме действующей программы. Студентам рекомендуется изучать материал по следующей методике:
1. Ознакомиться с содержанием программы.
2. Изучить материал по данным методическим указаниям, понять опорные термины, теоремы, запомнить формулы, разобраться в решении задач, которые приводятся в данных указаниях.
3. Изучит соответствующий материал курса по учебнику, составить его конспект.
4. Ответить на вопросы и выполнить упражнения, приведенные в конце каждой темы данных методических указаний.
К выполнению контрольной работы следует приступать только после овладения соответствующим материалом. При выполнении контрольной работы следует руководствоваться следующими указаниями:
1. Контрольную работу выполняют в отдельной тетради школьного образца в клетку. Следует пронумеровать страницы и оставить на ни поля, отступив не менее 3 см для замечаний преподавателя.
2. На обложку тетради приклеить титульный лист утвержденного образца и заполненного по форме.
3. Работу выполняют чернилами одного цвета, аккуратно и разборчиво.
4. Каждое задание выполняется с новой страницы.
5. Условие задач переписывать полностью в контрольную тетрадь.
6. Чертежи выполняются карандашом с использованием чертежных инструментов, аккуратно, соблюдая масштаб.
7. Решение задач должны сопровождаться краткими пояснениями, используемые формулы нужно выписывать.
8. Контрольная работа должна быть выполнена в срок в соответствии с учебным планом – графиком и кодом .
9. Работа, выполненная не по своему варианту, не учитывается и возвращается студенту.
Примерный тематический план.
| Наименование разделов и тем. | часы | Задания учащимся | ||
| Тема 1.1 Раздел 1 Действительные числа | 6 | |||
| 1 | Математика и НТП. Действительные числа. Вычисление значений выражений. | 2 | [Д.Л 1] Алгебра и начала анализа. Под ред. Г.Н. Яковлева, 1ч, §1, §8 | |
| 2 | Решение уравнений и неравенств первой степени. Решение квадратных уравнений и неравенств. Способы решений иррациональных уравнений и неравенств. | 2 | Л2], раздел 2, §1-4 [Д.Л1], 1 ч., §12 [Л1] Алгебра и начала анализа 10-11. Под ред.акцией А.Н Колмогорова, §9.33 | |
| 3 | Определители второго и третьего порядка. Системы линейных уравнений. | 2 | [Д. Л1],ч. I, §9, §10, ч. II , §2, §3, §4, [Л2] гл.3 §5. 6. | |
| Раздел 2. Последовательности и функции. | 6 | |||
| 10. | Числовая функция. Способы задания функции. Основные свойства функций. Графики функций. | 2 | [Л1], гл. 1. §2 [Д..Л1] §15. [Л2], гл.4 §1. [Л1] гл. 1 §2.3, гл. 5 §3 | |
| 11. | Предел функции в точке. Основные свойства предела. | 2 | Д. Л1],ч. I, гл. 4 §18.1-4 [Л2], гл. 6 §1, 2. | |
| 12. | Предел функции на бесконечности. Вычисление пределов. Первый и второй замечательные пределы. | 2 | [Д. Л1],ч. I, гл. 4 §18.1-4 [Л2], гл. 6 §1. [Д. Л1],ч. I, гл. 4 §30.1 [Л2], гл. 6 §2. | |
| 13. | Раздел 3. Показательная, логарифмическая и степенная функции | 10 | ||
| 14. | Степень с произвольным действительным показателем и ее свойства. Выполнение действий над степенями. | 2 | [Л1] гл. 4 §9 [Д. Л1], гл.5 §20.1. Л1] гл. 4 §9 [Д. Л1], гл.5 §20.1. | |
| 15. | Логарифмы и их свойства. Натуральные и десятичные логарифмы. Преобразование и вычисления значений логарифмических выражений. | 2 | Л1] гл. 4 §10.37 [Д. Л1], гл.5 §20.2 [Л2], гл.4 §2. Л1] гл. 4 §10.37 [Д. Л1], гл.5 §20.2 [Л2], гл.4 §2. | |
| 16. | Показательная функция, Логарифмическая функция, Степенная функция ее свойства и график. | 2 | [Л1] гл. 4 §10.35 [Д. Л1], гл.5 §21.1 [Л2], гл.4 §2. [Л1] гл. 4 §10.38 [Д. Л1], гл.5 §21.2 [Л2], гл.4 §2. Л1] гл. 4 §11.43 [Д. Л1], гл.5 §21.3. | |
| 17. | Показательные уравнения. Показательные неравенства | 2 | [Л1], гл. 4. §10.36 [Д..Л1] гл.5 §22.1 [Л2], гл.4 §3. [Л1], гл. 4. §10.36 [Д..Л1] гл.5 §22.3 [Л2], гл.4 §5. | |
| 11. | Логарифмические уравнения. Логарифмические неравенства | 2 | [Л1], гл. 4. §10.39 [Д..Л1] гл.5 §22.2 [Л2], гл.4 §6. Л1], гл. 4. §10.39 [Д..Л1] гл.5 §22.3 [Л2], гл.4 §8 | |
| Раздел 4. Тригонометрические функции | 8 | |||
| 12 | Основные тригонометрические тождества. Вычисление значений и тождественные преобразования тригонометрических выражений. | 2 | [Л1], гл. 5. §2.6 [Д..Л1] гл.5 §24.1,3 [Л2], гл.9 §1-6,14, 16, 19, 20. | |
| 13 | Свойства и график тригонометрической функции у=sinx. у=соsx, у= tgx, у= сtgх. | 2 | [Л1], гл. 1. §1.2 [Д..Л1] гл.5 §24.5 [Л1], гл. 1. §1.3 [Д..Л1] гл.5 §24.5 | |
| 14 | Способы решения тригонометрических уравнений | 2 | [Л1], гл. 1. §3.10 [Д..Л1] гл.5 §26 [Л2], гл.9 §9 [Л1], гл. 1. §3.9 [Д..Л1] гл.5 §26 [Л2], гл.9 §9, | |
| 15 | Тригонометрические неравенства. Решение простейших тригонометрических неравенств. | 2 | [Л1], гл. 1. §3.10 [Л2], гл.9 §10 | |
| Раздел 5. Дифференциальное исчисление | 8 | |||
| 16 | Определение производной, ее механический смысл. Общий метод нахождения производных | 2 | [Л1] Гл. 2 §5.21 [Д..Л1] Гл. 6 §27.1,3 [Л2], гл.7 § 1, 2 | |
| 17 | Правила дифференцирования функций. | 2 | [Л1] Гл. 2 §4.15-17 [Д..Л1] Гл. 6 §28 [Л2], гл.7 § 3 | |
| 18 | Нахождение производных функций. | 2 | [Л1] Гл. 2 §4, 5 [Д..Л1] Гл. 6 §27-31 [Л2], гл.7 § 1-4, 6, 7 гл.9 § 24 | |
| 19 | Применение производной к исследованию функций и построению графиков функций.. | 2 | [Л1] Гл. 2 §6.24 [Д..Л1] часть 1 Гл. 7 §33-35 [Л2], гл. 8 | |
| Раздел 6. Интегральное исчисление. | 8 | |||
| 20 | Первообразная. Основное свойство первообразной. | 2 | [Л1] Гл. 3 §7.26, 27, 28 | |
| 21 | Неопределенный интеграл и его свойства. Основные формулы интегрирования. Способы вычисление неопределенных интегралов | 2 | [Д.Л1] часть 2 Гл. 2 §5 [Л2], гл. 11§1 | |
| 22 | Определенный интеграл и его геометрический смысл. Вычисление определенного интеграла. | 2 | [Д.Л1] часть 2 Гл. 3 §7, 8.1 [Л1] Гл. 3 §8.29, 30 | |
| 23 | Вычисление площадей плоских фигур с помощью определенного интеграла | 2 | [Л1] Гл. 3 §8.29 Гл. 5 §5.25 [Д.Л1] часть 2 Гл. 4 §12 [Л2], гл. 13 §1 | |
| Раздел7. Комбинаторика, статистика, теория вероятностей. | 6 | |||
| 24 | Основные понятия комбинаторики. Перестановки, сочетания. Задачи на подсчет числа размещений, перестановок, сочетаний. | 2 | (Л2) стр. 257 №12-15 | |
| 25 | Определение вероятности. Событие, вероятность события, сложение и умножение вероятностей. Понятие о независимости событий. Задачи. | 2 | (Л2) ;п. 2, стр.260 П.3 стр.262 №33, №41 (Л4) стр.363-373 | |
| 26 | Элементы математической статистики. Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка, среднее арифметическое, медиана. | 2 | (Л.4)п. 17.3 , стр. 384-385 | |
| Раздел 8. Векторы и координаты | 2 | |||
| 27 | Векторы на плоскости. Действия над векторами. Разложение векторов на составляющие. | 2 | [Д.Л2] Гл. 1§1-9,Гл.5 [Д.Л3] Гл.1, 5 [Л2], гл.17, 21 | |
| Раздел 9. Прямые и плоскости в пространстве. | 2 | |||
| 28 | Аксиомы стереометрии и простейшие следствия из них | 2 | [Д.Л2] Гл. 4 §24 [Д.Л3] Гл. 4 §12 | |
| Раздел 10. Геометрические тела и поверхности. | 4 | |||
| 29 | Понятие о геометрическом теле и его поверхности. Многогранники. Понятие о правильных многогранниках. | 2 | [Д.Л2] Гл. 8 §46-49 [Д.Л3] Гл.4, §13, 15, 19 | |
| 30 | Поверхность вращения. Тела вращения. Цилиндр Конус Шар, сфера. | 2 | [Д.Л2] Гл. 8 §50 [Д.Л3] Гл.7, §30.1 1 | |
| Раздел 11. Объемы и площади поверхностей геометрических тел. | 6 | |||
| 31 | Объем геометрического тела. | 2 | [Д.Л2] Гл. 10 §58., 59, 61. [Д.Л3] Гл.8, §33, 35 | |
| 32 | Площадь поверхности геометрического тела. | 2 | [Д.Л2] Гл. 10 §60, 61 [Д.Л3] Гл.8 §37, Гл.4 §13 | |
| 33 | Решение геометрических задач. | 2 | [Д.Л2] Гл. 10 §60, 61 [Д.Л3] Гл.8 §37, Гл.4 §13 | |
| Всего 66 ч |
Учебное задание.
ЧАСТЬ 1
Действительные числа
Методические указания.
Студент должен знать: определения линейного и квадратного уравнения, формулы дискриминанта и корней квадратного уравнения, определение определителей второго и третьего порядка, формулировки теоремы Виета и теоремы Крамера.
Уметь решать линейные, квадратные уравнения и неравенства, Иррациональные уравнения, системы линейных уравнений, используя теорему Крамера.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Квадратные уравнения могут иметь два различных корня, один корень и не иметь корней.
Чтобы определить, сколько корней имеет уравнение надо найти дискриминант — это просто число D = b2 − 4ac.
Если D < 0, корней нет;
Если D = 0, есть один корень;
Если D > 0, корней будет два.
Если дискриминант D > 0, корни можно найти по формулам: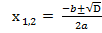
Квадратные неравенства можно решать двумя способами. Один способ - это метод интервалов. Другой способ: схематичный рисунок.
Определители второго и третьего порядка. Выражение
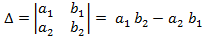называется определителем второго порядка.
Выражение
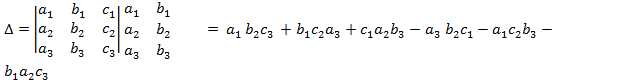называется определителем третьего порядка.
Теорема Крамера . Если определитель Δ системы линейных алгебраических уравнений с n неизвестными отличен от нуля, то эта система имеет единственное решение, которое находится по формулам Крамера: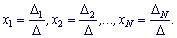
Примеры: Решить с помощью метода Крамера систему уравнений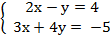
Решение: Δ =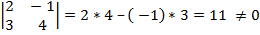
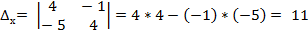
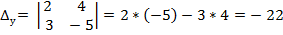
Х = 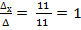У = =
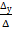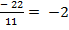
Ответ: (1; - 2 )
Дата: 2018-11-18, просмотров: 503.
