Студент должен знать: определение производной функции, механический и геометрический смысл производной, правила дифференцирования, алгоритм применения производной функции к исследованию и построению графика функции.

Уметь находить производную функции, применяя правила дифференцирования и таблицу производных, применять производную к нахождению промежутков монотонности функции и построению графиков функции.

Производная функции. Дана функция у = f(x). Пусть х₁ и х₂ – два значения аргумента,  а у₁ = f(x₁) и у₂ = f(x₂) – соответствующие значения функции у = f(x).

Разность ∆х = х₂ – х₁ называется приращением аргумента, а разность ∆у = у₂ – у₁ = f(x₂) - f(x₁) приращением функции на отрезке [ х₁; х₂ ]. Если у + ∆у = f(x +∆х ), то

∆у= = f(x +∆х ) – у или  ∆у= = f(x +∆х ) - f(x), тогда

 = .

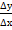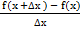Производной функции у = f(x) по переменной х называется предел отношения приращения функции к приращению аргумента х, когда ∆х стремится к нулю

    У^/ =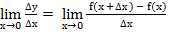  

Процесс нахождения производной называется дифференцированием.

Второй производной или производной второго порядка называется производная от ее производной    У^// .

Геометрический смысл производной. Производная функции у = f(x) в точке х = а равна угловому коэффициенту касательной, проведенной к графику данной функции в его точке с абсциссой х = а, то есть    У^/ = tg α , где α – угол наклона касательной к оси абсцисс.

Уравнение касательной в точке х₀. у = f(x₀) + f ^\ (x)(x – x₀).

Дифференциал функции. Из определения производной имеем    у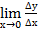^/ = , тогда величина  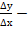у^/ есть бесконечно малая величина при ∆х →0.

Или, что то же самое: 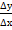 - f ^\ (x) = d(∆х), где d(∆х) →0 и ∆х →0, тогда

 ∆у = f ^\ (x) ∆х + d(∆х) ∆х.

Дифференциал функции у = f(x) в точке х называется главная часть f ^\ (x) ∆х приращения функции ∆у, линейно зависящая от приращения аргумента ∆х. Дифференциал обозначается символом dy.

Нахождение дифференциала функции называется дифференцированием, так же как и нахождение производной.

Производная сложной функции. Функция называется сложной, если ее аргументом является другая функция.

F(g(x)) ^] = F ^] *g ^}(x)  

Пример: у = (2х – 4)⁵

            У ^} =5 (2х – 4) ⁴*(2х – 4)^| = 10 (2х – 4)⁴

Правила дифференцирования.

Вынесение числового множителя: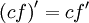   

Сумма :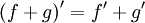

Произведение :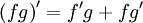

Частное :

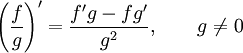
Примеры:

1) у^/ (х) = (х³ + 2 х² – 3х + 5)^/ = 3х² + 4 х – 3

2) у^/ (х)= ( =  =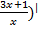

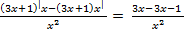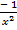
3) y^|(x) =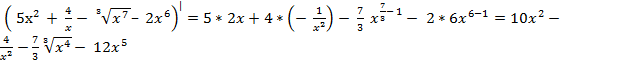

4) y^|(x)  = (( 5x – 3) * 2^x)^| =( 5x – 3)^|  *( 2^x) + ( 5x – 3) * (2^x)^|=( 5*1 – 0) 2^x +( 5x – 3)* 2^x*Ln 2 =

  = 5*2^x+( 5x – 3) 2^xLn 2

Функция у = f(x) называется непрерывной при заданном значении х,если она определена в некоторой окрестности этой точки и если бесконечно малому приращению х соответствует бесконечно малое приращение у.

Функция у = f(x) монотонно возрастает, если большему значению аргумента х соответствует большее значение функции. Условие возрастания: у^/ (х) > 0.

Функция у = f(x) монотонно убывает, если большему значению аргумента х соответствует меньшее значение функции. Условие убывания: у^/ (х) < 0.

Функция у = f(x) имеет максимум ( минимум) при х = а f ^/(x) = 0 , если при всех х, близких к а знак производной меняется с + на – ( с – на +).