Источники экономического роста

Вопрос о том, какие факторы влияют на экономический рост, остается одним из центральных вопросов макроэкономики, и дебаты по поводы источников экономического роста продолжаются и по сей день. Однако, большинство экономистов, следуя классической работе Роберта Солоу, выделяют следующие ключевые факторы экономического роста: технический прогресс, накопление капитала и рост трудовых ресурсов. Для того чтобы описать вклад каждого из этих факторов в экономический рост, рассмотрим выпуск Y, как функцию от запаса капитала (K), используемых трудовых ресурсов (L), и уровня технологии (А): Y=Y(K,L,A). Солоу рассматривал нейтральный технический прогресс, то есть, предполагал, что технический прогресс одинаково воздействует на предельный продукт труда и капитала:

Y=AF(K,L),                                                                                                        (1)

где F- неоклассическая производственная функция. Солоу также предполагал, что функция F обладает постоянной отдачей от масштаба, то есть, при увеличении количества капитала и труда в раз, выпуск также увеличивается в раз. Мы можем записать приращение выпуска как:

Поделив обе части соотношения на Y и, учитывая, что Y=AF(K,L), получим:

В условиях совершенной конкуренции предельный продукт труда равен реальной заработной плате, а предельный продукт капитала - реальной цене капитала. Таким образом, равняется доле дохода капитала в ВВП (s_K), а равняется доле оплаты труда в выпуске (s_L), причем для функции с постоянной отдачей от масштаба эти доли в сумме равны единице: s_L+s_K=1. Теперь мы можем переписать равенство (3) следующим образом:

Равенство (4) показывает, что темп роста выпуска () может быть разложен на три составляющие. Первая компонента в правой части -это накопление капитала, причем вклад капитала в рост ВВП пропорционален доле дохода капитала в выпуске. Вторая составляющая - это рост занятости, вклад занятости также пропорционален доли оплаты труда в ВВП. Наконец последняя компонента отвечает за вклад темпа роста технического прогресса в экономический рост.

Учитывая, что обычно под экономическим ростом понимают изменение выпуска на душу населения, вычтем из левой и правой части соотношения темп роста занятости:

Считая, что темп роста населения совпадает с темпом роста занятости, мы можем сказать, что темп роста производительности труда определяется темпом роста капиталовооруженности и темпом технологического прогресса.

Соотношение, демонстрирующее разложение темпа роста производительности труда на составляющие этого роста, называют разложением или декомпозицией Солоу.

Следует отметить, что в отличие от темпа роста производительности труда и капиталовооруженности, темп технологического прогресса практически невозможно измерить. Однако, используя соотношение мы можем определить темп технологического прогресса как разницу между наблюдаемым темпом роста выпуска на душу населения и темпом роста капиталовооруженности труда с поправкой на долю доходов капитала в ВВП:

Таким образом, экономический рост, не объясненный ростом капиталовооруженности, мы приписываем технологическому прогрессу, или, иначе говоря, мы получаем технический прогресс как остаток, который получил название остаток Солоу.

Базовый вариант модели Солоу (без технологического прогресса).

Рассмотрим однопродуктовую экономику. Пусть в этой экономике действует репрезентативный потребитель, который одновременно является производителем и владельцем факторов производства (экономика Робинзона Крузо). В экономике есть всего два фактора производства: труд и капитал, а выпуск в каждый момент времени t определяется производственной функцией: где F-производственная функция с постоянной отдачей от масштаба. Будем считать, что функция F возрастает по все аргументам, вогнута и удовлетворяет следующим техническим условиям: и

Будем рассматривать закрытую экономику без государственного сектора. Произведенная в момент t продукция может быть использована либо на потребление (C_t), либо на инвестиции (I_t):

Полученный доход потребитель распределяет между потреблением (C_t) и сбережениями (S_t), причем будем считать, что сбережения являются некой фиксированной долей дохода:

S_t=sY_t, где 0s1.

Через s обозначена норма сбережения, не зависящая от дохода и момента времени t, то есть, мы будем считать s экзогенным параметром. Будем считать, что капитал изнашивается с течением времени, и обозначим через (01) норму амортизации капитала, полагая ее постоянной. Таким образом, валовые инвестиции равны сумме чистого прироста капитала и амортизационных расходов: , где -чистый прирост капитала.

Будем считать, что население в рассматриваемой экономике равно трудовым ресурсам и растет с постоянным темпом n:  Будем также считать, что в экономике имеет место полная занятость, то есть труд, стоящий в производственной функции, равен занятости.

Поделим обе части уравнения на L_t и с учетом однородности первой степени функции F получим:

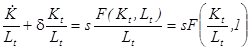(1)

Перейдем от абсолютных величин к величинам на одного рабочего, обозначив через k капитал на одного рабочего или капиталовооруженность (kK/L), а через f(k) - выпуск на одного рабочего или производительность труда (f(k) F(K/L,1)).

Стационарное состояние.

Определим стационарное состояние в рассматриваемой модели, как ситуацию, в которой капитал на одного рабочего является неизменным: .тационарная величина капиталовооруженности k* определяется из условия:

Поскольку капиталовооруженность в стационарном состоянии неизменна, то производительность труда и потребление на одного работника также постоянны и равны: y*=f(k*), c*=(1-s)f(k*), соответственно. Это значит, что запас капитала, выпуск и потребление в стационарном состоянии растут с тем же темпом, с которым растет население.

Стационарное состояние в модели Солоу можно изобразить графически. По нашим предположениям производственная функция f(k) вогнута и выходит из нуля. Кроме того, наклон f(k) в нуле равен бесконечности, а при больших k кривая f(k) становится пологой. Инвестиции, необходимые для поддержания постоянной капиталовооруженности, (n+)k изображены прямой линией, выходящей из нуля под углом, равным (n+). Если первоначально экономика имеет капиталовооруженность k₀, то валовые инвестиции на одного работника (i) для этой экономики будут равны сбережениям в точке k₀. Чистые инвестиции на одного работника соответствуют расстоянию между кривой сбережений sf(k) и линией необходимых инвестиций (n+)k. Потребление на душу население с соответствует вертикальному отрезку между производственной функцией и функцией сбережений.

Точка пересечения кривой сбережений и кривой необходимых инвестиций определяет стационарный уровень капиталовооруженности k*. Заметим, что стационарное состояние при положительной капиталовооруженности существует, поскольку функция f(k) вогнута, выходит из нуля и удовлетворяет следующим условиям: и .

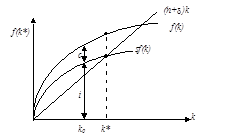
Рисунок 3.1 – Стационарное состояние в модели Солоу.

Золотое правило накопления капитала.

Из уравнения для стационарного состояния следует, что при изменении нормы сбережения изменяется и стационарная капиталовооруженность, а, соответственно, меняется и стационарное потребление на душу населения. Как изменяется потребление при изменении нормы сбережения? Ответ на этот вопрос зависит от первоначального состояния экономики. Стационарное потребление на душу населения растет с ростом s при низких нормах сбережения и падает при высоких. При какой норме сбережения стационарное потребление c будет максимальным?

Стационарное потребление на душу населения мы находим как разницу между доходом и сбережениями: c*=f(k*(s))-sf(k*(s)). Учитывая, что sf(k*)=(n+)k*, находим:

с*=f(k*(s))-(n+)k*(s).

Максимизируя по s, находим: Поскольку, то выражение в скобках должно быть равно нулю. Капиталовооруженность, при которой выражение в скобках равно нулю будем называть капиталовооруженностью, соответствующей золотому правилу. Итак, если мы будем поддерживать одинаковый уровень потребления для всех живущих ныне и для всех будущих поколений, то есть, если мы будем поступать с будущими поколениями так, как мы хотели бы, чтобы они поступали с нами, то - это максимальный уровень стационарного потребления на душу населения, который мы можем обеспечить.

Проиллюстрируем золотое правило графически. Норма сбережения s^g на рисунке 2 соответствует золотому правилу, поскольку стационарный капитал k^g таков, что наклон f(k) в точке равен (n+). Как видно из рисунка при увеличении нормы сбережения до или снижении до стационарное потребление на душу населения падает по сравнению с : и .

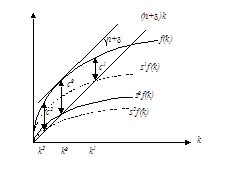
Рисунок 3.2 – Золотое правило накопления капитала.

Если норма сбережения в экономике превышает и, соответственно стационарная капиталовооруженность выше, чем при золотом правиле, то распределение ресурсов в такой экономике динамически неэффективно. Снизив норму сбережения до , можно было бы достигнуть не только повышения потребления на душу населения в долгосрочном периоде, т.е. роста стационарного c, но и в процессе перехода от стационарной капиталовооруженности к потребление на душу населения было бы выше, чем в исходном состоянии. Схематично изменение потребления на душу населения изображено на рисунке 3.3.

В момент снижения нормы сбережения потребление на душу населения резко растет, а затем монотонно падет до величины. С учетом того, что , получаем, что даже в течение перехода к новому стационарному состоянию экономика в каждый момент времени имеет более высокое потребление на душу населения, чем исходный уровень . Таким образом, экономика с нормой сбережения, превышающей , сберегает слишком много и в силу этого распределение ресурсов является динамически неэффективным.

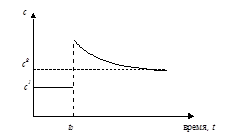
Рисунок 3.3 – Динамика потребления на душу населения при снижении нормы сбережения c уровня до величины.

Если норма сбережения в экономике меньше, то, увеличив норму сбережения до , можно было бы достигнуть более высокой стационарной капиталовооруженности, но в переходный период потребление было бы ниже, чем в настоящий момент. Таким образом, в данном случае нельзя однозначно утверждать, что подобное распределение ресурсов неэффективно, поскольку все зависит от того, как общество ценит будущее потребление относительно текущего, то есть, от межвременных предпочтений.

Как следует из анализа модели Солоу, поскольку в стационарном состоянии капиталовооруженность постоянна, то и производительность труда также будет постоянна, то есть, долгосрочный рост выпуска не зависит от экзогенных параметров таких, как норма сбережения, норма амортизации, а определяется исключительно темпом роста населения. Однако эти экзогенные параметры влияют на производительность труда в переходный период, то есть, при движении к стационарному состоянию.

Рассмотрим, чем же определяется темп роста капиталовооруженности на равновесной траектории, описываемой уравнением накопления капитала. Изобразим динамику модели Солоу. Заметим, что sf(k)/k убывает по k. Расстояние между кривыми sf(k)/k и (n+) по вертикали равно темпу роста капиталовооруженности. В точке пересечении кривых sf(k)/k и (n+) темп роста капиталовооруженности равен нулю, то есть мы находимся в стационарном состоянии k*. Справа от k* темп роста капиталовооруженности отрицателен, а слева- положителен.

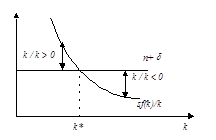
Рисунок 3.4 – Динамика темпа роста капиталовооруженности в модели Солоу.

Заметим, что динамика темпа роста производительности труда аналогична динамике темпа роста капиталовооруженности, поскольку

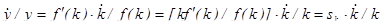
Сравнительная статика модели Солоу.

Анализируя стационарное состояние модели Солоу, можно заключить, что стационарная капиталовооруженность зависит от следующих экзогенных параметров: нормы сбережения, нормы амортизации и темпов роста населения.

1. Изменение нормы сбережения.

Если государству удастся каким-либо образом добиться повышения нормы сбережения, то график функции sf(k)/k сдвинется вверх и стационарный капитал возрастет, как показано на рисунке 5.

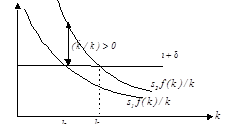
Рисунок 3.5 – Изменение капиталовооруженности в результате повышения нормы сбережения от до .

Как экономика движется к новому уровню стационарной капиталовооруженности ? Как следует из рисунка 8.5, за повышением нормы сбережения следует скачок в темпе роста капиталовооруженности, затем по мере увеличения капиталовооруженности расстояние между кривыми sf(k)/k и (n+) сокращается и устремляется к нулю. Таким образом, сразу вслед за повышением нормы сбережения темп роста капитала становится выше темпа роста населения, а по мере приближения к новому стационарному состоянию темпы роста K и L вновь сближаются.

На основе проведенного анализа можно заключить, что изменение нормы сбережения не оказывает влияние на долгосрочные темпы роста выпуска, но влияет на темпы роста в процессе движения к стационарному состоянию. Так увеличение нормы сбережения приводит к резкому повышению темпов роста производительности труда, однако, по мере приближения к стационарному состоянию этот эффект сходит на нет.

2. Изменение темпов роста населения.

В результате повышения темпов роста населения стационарная капиталовооруженности будет падать, то есть, в терминах рисунка 6 последствия могут быть представлены как переход из в .

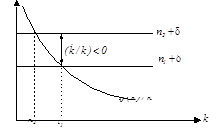
Рисунок 3.6 – Изменение капиталовооруженности в результате увеличения темпа роста населения от до .

Таким образом, процесс перехода к новому стационарному состоянию будет сопровождаться резким падением темпов роста капиталовооруженности с последующим медленным восстановлением до исходного уровня. Аналогична и динамика производительности труда. Темп роста производительности труда сначала станет отрицательным, а затем будет расти, пока не вернется к нулевой отметке, при этом темп роста самого выпуска в новом стационарном состоянии будет выше, чем в первоначальном, как показано на рисунке 9.7.

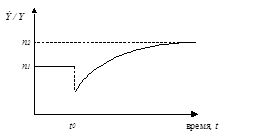
Рисунок 3.7 – Динамика темпа роста выпуска при увеличении темпа роста населения с n1 до n2.

Недостатки модели Солоу.

Модель Солоу объясняет долгосрочный экономический рост экзогенным показателем, отражающим темп технического прогресса. При этом остается непонятным, что определяет этот темп и может ли экономическая политика способствовать увеличению темпов экономического роста.

Другая проблема, связанная с моделью состоит в том, что согласно модели Солоу различия в производительности труда между богатыми и бедными странами являются результатом различий в уровнях капиталовооруженности, что, в свою очередь, объясняется различиями в нормах сбережения, амортизации, темпах роста населения и темпах технического прогресса. Рассмотрим две экономики с одинаковой технологией, но разным уровнем капиталовооруженности (см. рис.8).

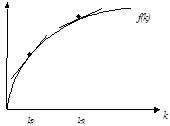
Рисунок 3.8 – Отдача на капитал в богатой и бедной стране в модели Солоу.

Пусть богатая страна находится в точке , а бедная страна в точке . Это означает, что предельный продукт капитала должен быть выше в бедной стране по сравнению с богатой, что для многих бедных стран не соответствует действительности (если бы это было так, то мы должны были бы наблюдать значительный приток капиталов в бедные страны).