Анотація

Інтегровані критерії точності й адекватності. Поняття комбінованого прогнозу. Алгоритм об’єднання окремих прогнозів. Методи об’єднання прогнозів: дисперсійно-коваріаційний, регресійний.

10.1 Інтегровані критерії точності й адекватності.

Схема формування інтегрованих критеріїв точності й адекватності, а також загального критерію якості прогнозування полягає у тому, що формується склад окремих критеріїв, на підставі яких обчислюють інтегрований показник (скажімо, точність можна характеризувати лише коефіцієнтом детермінації, або дисперсією та середньою помилкою апроксимації, або всіма переліченими критеріями).

Попередньо для кожного окремого критерію розробляють процедуру його нормування. Нормований критерій одержують із вихідної статистики критерію таким чином, щоб виконувалися умови: нормований критерій дорівнює 100, якщо модель абсолютно точна (адекватна), нормований критерій дорівнює 0, якщо модель абсолютно неточна (неадекватна).

Узагальнений критерій якості моделі розраховують як зважену суму узагальненого критерію точності (його вага 0,75) і узагальненого критерію адекватності (його вага 0,25), тобто віддають перевагу точності. За характеристику точності обирають нормоване значення середньої відносної похибки апроксимації, а за критерій адекватності — нормоване значення критерію Дарбіна-Ватсона та характеристики нормального закону розподілу залишкової компоненти. Числове значення узагальненого критерія якості перебуває у діапазоні від 0 до 100 (мінімум відповідає абсолютно неправильній моделі, а максимум — моделі, що ідеально відображає розвиток показника). Досвід застосування цього показника свідчить про надійність моделей, оцінка якості яких не менша за 75.

Наведені вимірювання якості прогнозу виходять із незначного відхилення його від фактичних значень, але зрозуміло, що деякі змінні прогнозувати простіше, ніж інші. Так, вважається, що обсяг поточного рахунка платіжного балансу, який визначається як різниця двох великомасштабних показників — імпорту та експорту, — прогнозувати важче, ніж величини, які змінюються відносно повільно, наприклад тривалість життя, рівень безробіття. Отже, для визначення оптимального прогнозу необхідний системний критерій. Точніше оптимальний прогноз слід визначати з розгляду функції витрат користувача прогнозу, тобто з аналізу збитків через помилку прогнозу, а також із порівняння додаткового виграшу від зменшення помилки та витрат на вдосконалення прогнозу. Таким чином, оптимальним вважається найкращий прогноз, який можна одержати за наявних обставин.

Узагальнюючи огляд критеріїв визначення якісного прогнозу, можна зробити висновок, що потрібно користуватися системою критеріїв, які повинні враховувати:

- кількість зусиль, що витрачаються на побудову моделі і наявність готових комп’ютерних програм;

- швидкість, із якою метод уловлює істотні зміни у поведінці ряду, наприклад, раптовий зсув математичного сподівання або збільшення кута нахилу лінії тренду;

- існування серійної кореляції у помилках;

- незмінюваність первинних даних;

- повний обсяг роботи у деяких сферах діяльності – тисячі рядів щомісяця потребують оновлення, невеликі витрати і швидкість мають першорядне значення;

- терміновість прогнозування.

10.2. Поняття комбінованого прогнозу

Серед дослідників немає єдиної думки щодо існування найкращого методу прогнозування. Досвід застосування різноманітних підходів до прогнозування доводить, що кожен метод призводить до різних результатів. Отже, як правило, виходить кілька відмінних прогнозів одного економічного показника. Постає питання: чи переважає якийсь метод решту, і чи можливо якимось чином скомбінувати прогнози, одержані різними методами, щоб побудувати узагальнений прогноз, який буде точніший за індивідуальні?

Можна сподіватися, що будь-який прогноз, відкинутий через його неоптимальність, майже завжди містить певну корисну незалежну інформацію. Така інформація може бути двосторонньою: по-перше, кожен прогноз ґрунтований на інформації, яка є спеціальною для цього підходу, і тому не враховується в інших методах; по-друге, кожен прогноз відтворює певну форму взаємозв’язків між змінними, що відрізняється від зв’язків, досліджуваних в інших моделях. Об’єднання незалежно одержаних прогнозів залучає обидва види додаткової інформації, і якщо припустити, що кожна з моделей описує лише один бік динаміки заданого процесу, то використання кількох моделей уможливить точніший і повніший опис і прогнозування динаміки. Не випадково сучасна теорія систем пропонує стратифікований підхід до опису складних систем. Така точка зору сприяла ідеї об’єднання прогнозів і формування на цій основі комбінованого, або об’єднаного прогнозу.

Об’єднання можна здійснювати як на підставі прогнозів, отриманих із різних джерел, наприклад, експертним шляхом і за допомогою моделей, так і із застосуванням, побудованими за допомогою статистичних моделей одного класу.

Спосіб об’єднання окремих прогнозів, як правило, полягає в тому, щоб представити комбінований прогноз у вигляді зваженої суми окремих прогнозів:

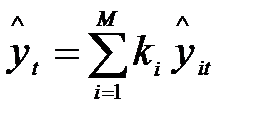,                                      (10.1)

де y_it— і-й окремий прогноз, одержаний для моменту часу t;

М — кількість об’єднуваних прогнозів;

k_i — вагові коефіцієнти окремих прогнозів. 0 ≤ k ≤1.

Сума всіх вагових коефіцієнтів має давати одиницю, кремі ваги мають перебувати в інтервалі [0, 1]. Очевидно, що головна проблема, яка при цьому виникає, — визначення ваг k_i, оскільки саме вони визначатимуть якість об’єднаного прогнозу. На практиці завжди прагнуть надати більшої ваги тому набору прогнозів, який містить менші за величиною середньоквадратичні похибки. Існує чимало способів визначення вагових коефіцієнтів, найвідомішими серед яких є два:

- дисперсійно-коваріаційний метод, що дає змогу зводити кілька незміщених прогнозів у лінійну комбінацію з найменшою дисперсією. Вагові коефіцієнти окремих прогнозів залежать від дисперсій та коваріацій похибок прогнозів;

- регресійний метод, який є узагальненням дисперсійно-коваріаційного на випадок зсуненості прогнозів.

Розглянемо метод, при якому вагові коефіцієнти визначаються з умови мінімуму дисперсії помилок узагальненого прогнозу (максимуму його точності), яка знаходиться як сума всіх елементів коваріаційної матриці помилок окремих прогнозів із відповідними вагами.

10.3. Алгоритм об’єднання прогнозів

Алгоритм об’єднання окремих прогнозів має такі кроки:

1. Обчислюються дисперсії помилок окремих прогнозів і будується коваріаційна матриця:

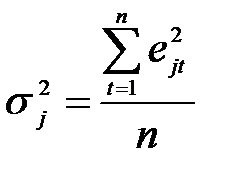, j = 1 ,…, M,                              (10.2)

де e_j – помилки окремих прогнозів;

t – порядковий номер спостереження, t = 1 ,…, n;

.

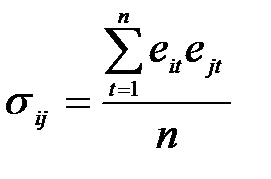2. Будуються матриця В і вектор С за формулами:

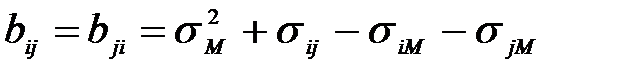;                        (10.3)

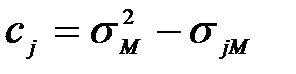.                                   (10.4)

3. Через розв’язання системи лінійних рівнянь одержують (М – 1) значення р_j, при цьому значеневий коефіцієнт р_М визначається як:

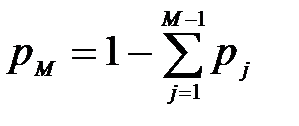.                                      (10.5)

4. Перевіряється умова: p_j > 0, j = 1 ,..., М.

При цьому:

а) якщо умова не виконується, прогнози виключаються і перераховуються вагові коефіцієнти (із поверненням до п. 2);

б) якщо всі вагові коефіцієнти додатні, то розраховується значення узагальнюючого прогнозу F і коефіцієнт умовної ефективності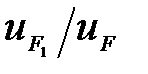

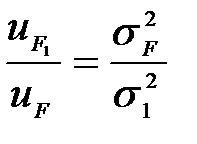; ,                           (10.6)

де  – дисперсія помилок комплексного прогнозу;

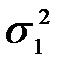 – дисперсія помилок найкращого окремого прогнозу.

5. Оскільки в більшості випадків точність прогнозів змінюється в часі, формули оцінки вагових коефіцієнтів модифікуються так, щоб пізнішим помилкам надати більшого значення. Отже, шляхом зміни вагових коефіцієнтів у бік найкращого окремого прогнозу F_jt коригується узагальнений прогноз:

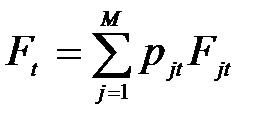,                                   (10.7)

де p_jt – вагові коефіцієнти окремих прогнозів у момент часу t;

F_jt – окремий прогноз у момент часу t;

F_t – узагальнений прогноз у момент часу t.

Для підвищення стабільності динаміки зміни ваги в алгоритмі її коригування можна використовувати схему експоненційного згладжування.

У цілому для проведення узагальнення необхідно мати не менше двох адекватних моделей, а для підвищення стійкості результатів кількість узагальнюваних окремих прогнозів не повинна перевищувати п’яти.

Спосіб комбінування прогнозів, одержаних за статистичними моделями одного класу, породжує низку питань. Наприклад, які прогнози можуть об’єднуватися, якою має бути кількість прогнозів та процедура об’єднання тощо. Об’єднання прогнозів пов’язано з такими ускладненнями, як корельованість прогнозів, одержаних за різними моделями, властивість похибок прогнозу змінюватися із часом, зміщення комбінованого прогнозу тощо.Кожне з названих ускладнень потребує застосування спеціального підходу. Поки не розроблено єдиних правил, суб’єктивні судження дослідника є складовою прийняття рішення стосовно того, як комбінувати прогнози.

10.4. Методи об’єднання прогнозів

Дисперсійно-коваріаційний метод. Об’єднання прогнозів розглянемо на прикладі побудови середньозваженого прогнозу двох окремих прогнозів, оскільки поширення одержаних результатів на більшу кількість окремих прогнозів здійснюється досить просто. У загальному випадку два незсунені прогнози можна скомбінувати для одержання нового прогнозу. Будемо виходити з мінімізації дисперсії похибки прогнозу, тобто використовувати квадратичну функцію збитків.

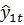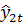Нехай маємо на період t два незсунені прогнози і , дисперсії яких  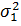та 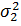 і коваріація 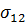. Новий незсунений прогноз  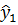будується за правилом

.                            (10.8)

Дисперсія похибки комбінованого прогнозу дорівнюватиме:

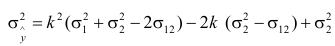.             (10.9)

Мінімізуючи цей вираз за k , одержимо, що

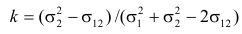.                   (10.10)

Отже, ваги в оптимальній лінійній комбінації залежать від дисперсій та коваріацій похибок прогнозу, звідки й походить назва дисперсійно-коваріаційний метод.

Кореляція між похибками окремих прогнозів дорівнює 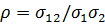, підстановка замість  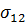та k у (10.23) дає

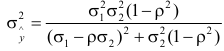.                     (10.11)

Звідси можна показати, що ( 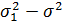) ≥ 0 та ( 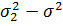) ≥ 0 і 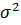менше або дорівнює мінімальному з  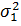та 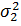. Отже, комбінований прогноз принаймні не менш точний за кращий із двох прогнозів, які взято як компоненти.

Оптимальну величину k не можна одержати на початковій стадії синтезу прогнозу, оскільки вона змінюється мірою накопичування знань про відносну ефективність двох окремих прогнозів. Більше того, на попередній стадії ще невідомі ані дисперсії похибок окремих прогнозів 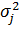, ані коефіцієнти кореляції між цими похибками. Їх треба оцінювати. Узагальнення цього методу до комбінування M прогнозів відбувається за формулою:

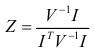,                                         (10.12)

де V — коваріаційна матриця похибок прогнозу розмірності M × M;

I — M-мірний вектор-стовпчик, усі координати якого є одиницями.

Аналіз знайдених оптимальних ваг дає підстави для таких висновків:

ü по-перше, очевидно, що інтуїтивна привабливість простого вибору найкращого (із найменшою дисперсією похибки) прогнозу та його використання здається сумнівною, оскільки в загальному випадку комбінований прогноз має меншу дисперсію похибки;

ü по-друге, якщо 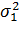 та 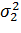 дорівнюють один одному, то у ваги також рівні, а комбінований прогноз є простим середнім значенням компонентів.

ü по-третє, якщо коваріація похибок прогнозів додатна й більша за одну із дисперсій (наприклад, якщо 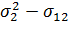 від’ємне), одна вага буде від’ємною, а інша перевищуватиме одиницю. Зауважимо, що від’ємність ваги не обов’язково свідчить про хибність прогрнозу;

ü по-четверте, коли дисперсія похибки прогнозу прямує до нуля, вага цього прогнозу прямує до одиниці. Отже, чим надійніший прогноз, тим більшу вагу він має.

Регресійний метод є узагальненням дисперсійно-коваріаційного методу. Його можна тлумачити як оцінювання параметрів регресійного рівняння виду

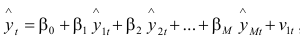,                 (10.13)

де збурення v має нульове середнє.

Новий комбінований прогноз є лінійною комбінацією М прогнозів. Коефіцієнти β_i, i = 0, 2, ..., M оцінюють за методом найменших квадратів. Якщо всі прогнози є незсуненими, то доданок β₀ можна опустити. У цьому разі значення коефіцієнтів збігатимуться із оцінками вектора Z із попереднього методу.