Анотація

Основні види кривих підгонки. Коефіцієнт детермінації та інші способи оцінки моделей. EX POST як імітація процесу прогнозування.

2.1 Основні види кривих підгонки

Метод підгонки входить до числа найвідоміших методів прогнозування. Він полягає в тому, щоб знайти криву або групу кривих, які з достатньою точністю описували б початкову інформацію. Розрізняють наступні види кривих підгонки: лінійна, параболічна, поліноміальна 3 ступеню, логарифмічна, експоненційна, ступенева, гіперболічна, логістична, S-образна. Існують і інші види кривих, але перелічені криві є найбільш поширеними і вживаними.

Рівняння прямої підгонки 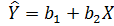 називається лінійним рівнянням регресії У по X (у прогнозуванні оцінене значення змінної прийнято позначати з кришкою вгорі: 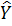) (див. рис. 2.1).

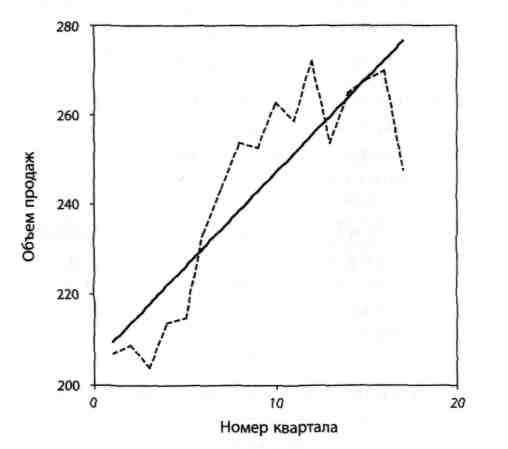
Рисунок 2.1 – Лінія регресії

Рівняння параболи має наступний вигляд 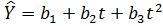 . На рис. 2.2 зображений графік параболи.

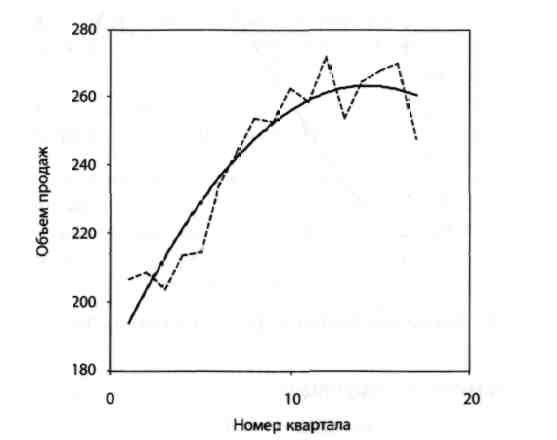
Рисунок 2.2 – Крива підгонки – парабола

Рівняння третього ступеня має вигляд 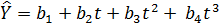 (див. рис. 2.3):

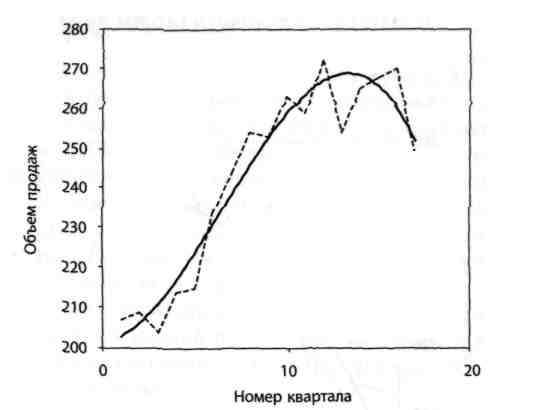
Рисунок 2.3 – Крива підгонки – графік многочлена третього ступеня

Рівняння логарифмічної функції має вигляд: 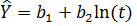 (див. рис. 2.4).

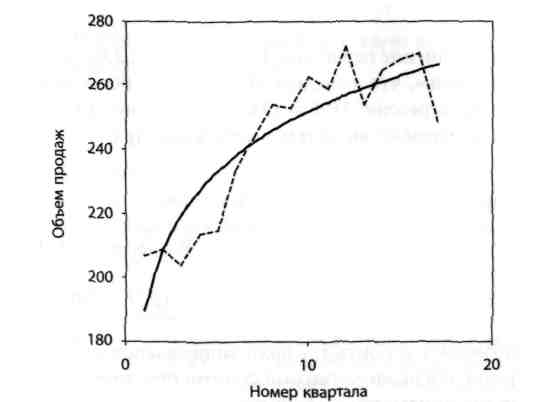
Рисунок 2.4 – Крива підгонки – графік логарифмічної функції

Рівняння експоненціальної кривої має вигляд: 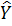 = b₁ exp ( b₂t ).

Ми нагадаємо, що exp(z)= e^z, де е ≈ 2,718. Зважаючи на важливість цього виду рівнянь для прогнозування, ми зупинимося на ньому докладніше. Розглянемо темп зростання у момент t.

.

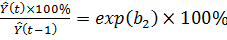Ми бачимо, що темпи зростання для експоненціальної кривої на даному інтервалі постійні. Оскільки e^z - 1 ≈ z при малих значеннях z, то b₂ × 100% приблизно рівно темпам приросту (див. рис. 2.5).

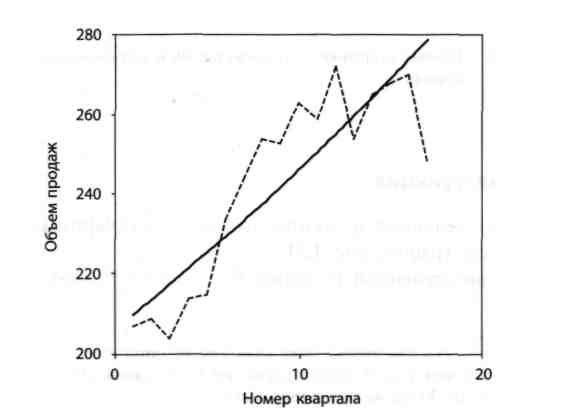
Рисунок 2.5 – Крива підгонки – експоненціальна крива

Рівняння ступеневої функції виглядає таким чином: 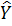 = b₁ (t^b2) (див. рис. 2.6).

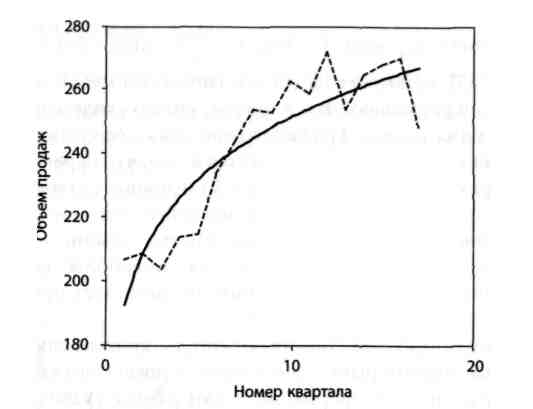
Рисунок 2.6 – Крива підгонки – графік ступеневої функції

Рівняння гіперболи має вигляд: 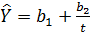 (див. рис. 2.7).

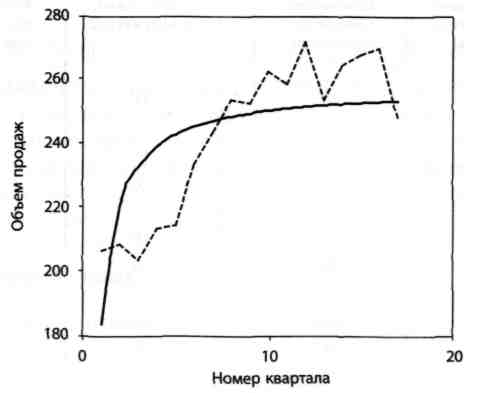
Рисунок 2.7 – Крива підгонки – гіпербола

Рівняння S-образної кривої має вигляд: 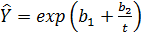. Як видно з цього рівняння, S-образна крива виходить шляхом послідовного застосування гіперболічної і експоненціальної функцій (див. рис. 2.8).

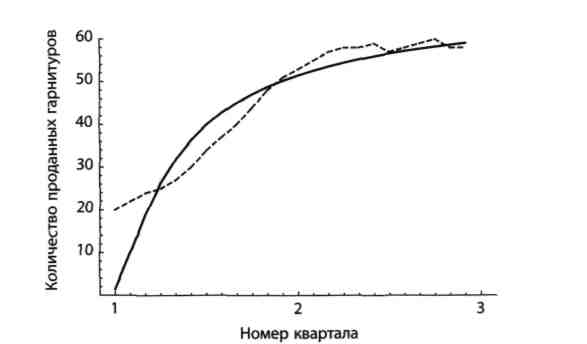
Рисунок 2.8 – Крива підгонки – S-образна крива

Рівняння логістичної кривої має вигляд 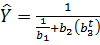 (див. рис. 2.9).

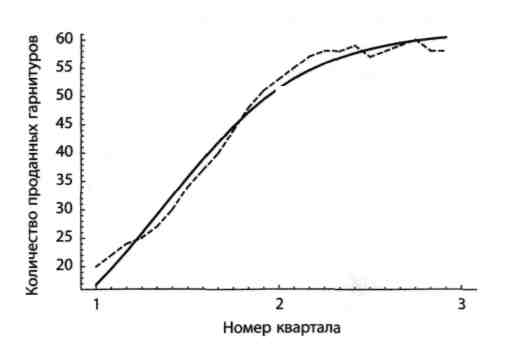
Рисунок 2.9 – Крива підгонки – логістична крива

2.2 Коефіцієнт детермінації та інші способи оцінки моделей

Середньо квадратична помилка (mean squared error, MSE) розраховується за формулою:

,

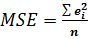де: n – кількість спостережень;

е – залишок, який визначається, як ;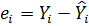

Yi – фактичне значення показника;

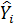 – теоретичне значення показника.

Коефіцієнт детермінації характеризує ступінь близькості змодельованих значень в їх сукупності до початкових даних. Коефіцієнт детермінації визначається виразом 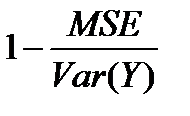 і позначається як R². Отже, коефіцієнт детермінації:

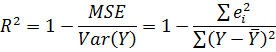
(2.1)

де: 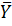 – середнє значення показника.

З визначення виходить, що R² ≤ 1. Рівність R² = 1 можливо тоді і тільки тоді, коли всі залишки рівні нулю, тобто процес в точності описується моделлю; проте на практиці цього майже ніколи не трапляється. З (2.1) витікає, що для одного і того ж набору даних коефіцієнт детермінації R² буде ближчим до одиниці у моделі з меншою середньоквадратичною помилкою. Таким чином, R² дійсно характеризує ступінь близькості змодельованих даних в їх сукупності до початкових даних. З формули (2.1) також витікає, що значення коефіцієнта детермінації залежить від дисперсії початкових даних. Наприклад, моделі для двох різних рядів даних можуть мати одні і ті ж значення залишків е₁, е₂, ..., е_n, але ряд даних з великим значенням дисперсії матиме і більше значення коефіцієнта детермінації.

Важливо пам'ятати, що R² – це всього лише позначення і, взагалі кажучи, може бути негативним числом.

У разі лінійної регресії невід’ємне число 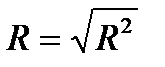 називається коефіцієнтом множинної кореляції і використовується набагато рідше, ніж коефіцієнт детермінації.

R² є часткою від ділення дисперсії змодельованих значень на дисперсію початкових. У ідеальному випадку, коли R² = 1, Var( 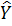)= Var(Y). Всі крапки (Х₁, Y₁), (X₂, Y₂), ..., (Х_n, Y_n) лежать на одній і тій же прямій тоді і тільки тоді, коли |р(Х, У)| = 1. р може приймати негативні значення, а R, за визначенням, повинен бути завжди більше або рівний нулю.

Коефіцієнт детермінації, безумовно, є важливим критерієм при виборі моделі. Якщо модель погано описує початкові дані, від неї не можна чекати добрих результатів при прогнозуванні. На жаль, зворотне невірне.

При порівнянні різних моделей крім коефіцієнта детермінації R² використовуються також дві інші характеристики – MAD і МАРЕ.

Вираз 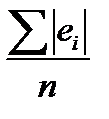 називається середнім абсолютним відхиленням (mean absolute deviation, MAD).

Вираз 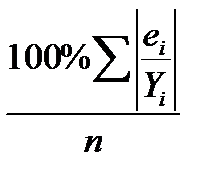 називається середньою абсолютною помилкою у відсотках (mean absolute percent error, МАРЕ).

На відміну від R², і MAD, і МАРЕ мають простий наочний сенс, що важливе для їх практичного застосування.

MAD і МАРЕ виявляються корисними при порівнянні залишків окремих значень моделі.

2.3 Верифікація прогнозів. EX POST як імітація процесу прогнозування

Статистичні прогнози ґрунтуються на гіпотезах про стабільність значень величини, що прогнозується; закону її розподілу; взаємозв'язків з іншими величинами тощо. Основний інструмент прогнозування — екстраполяція.

Суть прогнозної екстраполяції полягає в поширенні закономірностей, зв'язків і відношень, виявлених в t-му періоді, за його межі.

 Залежно від гіпотез щодо механізму формування і подальшого розвитку процесу використовуються різні методи прогнозної екстраполяції. Їх можна об'єднати в дві групи:

- екстраполяція закономірностей динаміки — тренду і коливань;

- екстраполяція причинно-наслідкового механізму формування процесу — факторне прогнозування.

Ці методи різняться не процедурою розрахунків прогнозу, а способом описування об'єкта моделювання. Екстраполяція закономірностей розвитку ґрунтується на вивченні його передісторії, виявленні загальних і усталених тенденцій, траєкторій зміни в часі. Абстрагуючись від причин формування процесу, закономірності його розвитку розглядають як функцію часу. Інформаційною базою прогнозування слугують одномірні динамічні ряди.

При багатофакторному прогнозуванні процес розглядається як функція певної множини факторів, вплив яких аналізується одночасно або з деяким запізненням. Інформаційною базою виступає система взаємозв'язаних динамічних рядів. Оскільки фактори включаються в модель у явному вигляді, то особливого значення набуває апріорний, теоретичний аналіз структури взаємозв'язків.

Важливим етапом статистичного прогнозування є верифікація прогнозів, тобто оцінювання їх точності та обґрунтованості. Ha етапі верифікації використовують сукупність критеріїв, способів і процедур, які дають можливість оцінити якість прогнозу.

Найбільш поширене ретроспективне оцінювання прогнозу, тобто оцінювання прогнозу для минулого часу (ex-post прогноз). Процедура перевірки така. Динамічний ряд поділяється на дві частини: перша — для t= 1,2,3, ...,p — називається ретроспекцією (передісторією), друга — для t=p + 1, p + 2, p + 3, ..., p +(n —р) — прогнозним періодом.

За даними ретроспекції моделюється закономірність динаміки і на основі моделі розраховується прогноз Y_p+v, де v — період упередження. Ретроспекція послідовно змінюється, відповідно змінюється прогнозний період, що унаочнює рис. 2.10 (для v = 1).

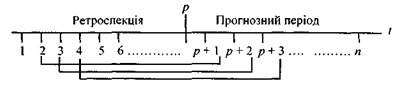
Рис. 2.10 – Схема ретроспективної перевірки точності прогнозу для v = 1

Оскільки фактичні значення прогнозного періоду відомі, то можна визначити похибку прогнозу як різницю фактичного у _t  і прогнозного Y_t рівнів: e_t = y_t – Y_t . Всього буде n —р похибок. Узагальнюючою оцінкою точності прогнозу слугує середня похибка:

абсолютна 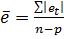, квадратична .

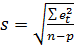Для порівняння точності прогнозів, визначених за різними моделями, використовують похибку апроксимації (%):

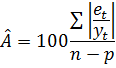
Якщо результат оцінювання точності прогнозу задовольняє визначені критерії точності, скажімо, 10%, то прогнозна модель вважається прийнятною і рекомендується для практичного використання. Очевидно, що похибка прогнозу залежить від довжини ретроспекції та горизонту прогнозування. Оптимальним співвідношенням між ними вважається 3 : 1.

При оцінюванні та порівнянні точності прогнозів використовують також коефіцієнт розбіжності Г. Тейла, який дорівнює нулю за відсутності похибок прогнозу і не має верхньої межі:

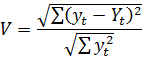
Існуючі методи верифікації прогнозів у більшості своїй ґрунтуються на статистичних процедурах, які зводяться до побудови довірчих меж прогнозу, себто до побудови інтервальних прогнозів.

Помилки ex post прогнозів можна оцінювати таким же чином, як ми оцінювали залишки моделі. Тобто ми можемо розглянути відповідні значення MSE, MAD і МАРE.

Для оцінки помилок ex post прогнозів використовується також число, яке називається коефіцієнтом нерівності Тейла (Theil's inequality coefficient):

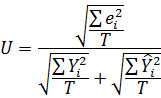
де T – число ex post прогнозів.

Еx post – один з найнадійніших методів при виборі моделі прогнозування. При цьому особливу увагу слід звертати на останні значення моделі. Стабільність коефіцієнтів моделі, разом з іншими характеристиками, які вказують на достатньо високу точність (R², MAD і МАРE), говорить на користь вибраної моделі.

Перш ніж приступити безпосередньо до прогнозування майбутніх значень, прогнозист повинен спочатку зрозуміти ті кількісні закономірності (або хоча б частина з них), які лежать в основі бізнес-процесу. Єдине, що він має в розпорядженні, це початкові дані. Звідси витікає, що на початку прогнозист повинен створити модель, яка достатньо добре описувала б саме початкові дані. Різниця між істинним і прогнозованим значеннями називається помилкою прогнозу.

Тут потрібно відзначити, що прогнозовані значення необов'язково повинні відноситися до майбутнього. Прогнозувати можна будь-які величини, що не входять в набір початкових даних. Подібні прогнозовані значення часто використовуються, коли необхідно відновити дані, відсутні через які-небудь причини.

Ідея ex post прогнозування. З цією метою початкові дані розбиваються на дві групи, так щоб в другій групі знаходилися пізніші дані, що становлять звично приблизно 15% всієї інформації. Ці дані будуть потім використовуватися для тестування. При невеликому об'ємі початкових даних в другій групі можна розглядати до 30% початкової інформації.

Але спочатку ми повинні задати горизонт прогнозування. При цьому кожного разу ми порівнюватимемо набуті значення з наявною інформацією. У цьому якраз і полягає головна перевага ex post прогнозування. При звичному прогнозуванні у нас такої можливості немає. Припустимо, що нас цікавить прогноз на один квартал вперед і ми хочемо протестувати лінійну модель. Нижче ми приводимо докладний алгоритм ex post прогнозування.

Алгоритм ex post прогнозування:

1. Знаходимо лінію регресії L для перших 13 значень.

2. З рівняння L визначаємо прогноз на 14-й квартал.

3. Порівнюємо одержаний прогноз з наявною інформацією за 14-й квартал. Знаходимо помилку.

4. Повторюємо пункти 1-3 послідовно для перших 14, 15 і 16 значень.

В результаті ми одержуємо таблицю, що містить ex post прогнози і відповідні помилки для останніх чотирьох кварталів.

В процесі ex post прогнозування, додаючи нові дані, ми кожного разу одержували інше рівняння. Це приклад рекурсивного ex post прогнозування, на відміну від нерекурсивного, при якому рівняння, одержане за даними першої групи, залишається незмінним.