Анотація
Оцінка ступеня узгодженості думок. Аналіз результатів опитування експертів. Експертні оцінки і моделі бінарного вибору. Моделі множинного вибору в експертному оцінюванні майбутнього.
8.1 Визначення кількісних параметрів і показників експертного опитування
Оцінка ступеня узгодженості думок.
Оцінкою відносної важливості напрямків (факторів, параметрів) не обмежується обробка даних опитувальних анкет.
Не менш важливі питання для наукового обґрунтування прогнозу мають оцінки відносної важливості, які характеризують:
а) узагальнену думку групи експертів стосовно відносної важливості розвитку різних об’єктів;
б) рівень узгодженості думок експертів;
в) «активність» експертів (міра їхньої участі в оцінюванні різних об’єктів);
г) компетентність експертів з кожного із запропонованих питань.
Дані експертизи являють собою сукупність оцінок, наданих кожним експертом кожному з оцінюваних ним об’єктів прогнозування. Ці оцінки виражають у балах (наприклад, від 0 до 100).
а) В економічному прогнозуванні широке розповсюдження отримала оцінка порівняльної важливості окремих факторів (параметрів, напрямків). Оцінка експертом відносної важливості факторів здійснюється, як правило, шляхом присвоєння деякої кількісної оцінки, наприклад, за 100-бальною системою. Експерт надає кожному фактору (параметру, напрямку) кількість балів в межах від 0 до 100. Нуль присвоюється в тому випадку, якщо фактор, на думку експерта, не має суттєвого значення; 100 балів присвоюється тому фактору, який має найбільш важливе вирішальне значення. Експерт може надати однакову кількість балів декільком факторам, якщо на його думку вони в рівному ступені суттєві. При обробці матеріалів колективної експертної оцінки відносної ваги факторів (параметрів, напрямку) доцільно використовувати метод рангової кореляції. Тому дані оцінені в балах, відповідним чином ранжують по мірі зменшення та отримують оцінки рангів. Порядковий номер, що визначає місце кожного фактора в загальній сукупності факторів, називається рангом. Зазвичай ранги відповідають числам натурального ряду 1, 2, 3, ... , n, де n – кількість ранжованихфакторів. Ранг, рівний одиниці, присвоюється найбільш важливому фактору; ранги із максимальним числом n – найменш важливому фактору. Якщо експерт присвоює однакову кількість балів декільком факторам, то їм присвоюється стандартизовані ранги. Стандартизований ранг – це частка від ділення суми місць, зайнятих факторами з однаковими рангами, на загальну кількість таких альтернатив.
При обробці результатів експертних оцінок по відносній важливості напрямків визначається ряд статистичних характеристик, на основі яких оцінюється кожний напрямок (параметр, фактор).
Сума рангів, призначених експертами j-ому напрямку досліджень, визначається за формулою:
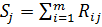(8.1)
де Rij— ранг наданий i -м експертом об’єкту j.
Очевидно, що під час порівняння значущості різних об’єктів найважливішим слід вважати той, що характеризується найбільшим значенням Si.
Середній ранг для кожного напрямку дорівнює:
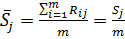(8.2)
Поряд з середніми рангами для кожного напрямку визначається середня величина в балах:
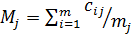(8.3)
При оцінці важливості окремих напрямків представляє інтерес показник частота максимально можливих оцінок, що визначається за формулою:
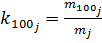(8.4)
де m 100 j— кількість 100-бальних оцінок, наданих j-му об’єкту.
Цю величину розраховують для кожного з m напрямів досліджень, вона може коливатися у межах від 0 до 1. Нижня межа відповідає випадку, коли серед оцінок, одержаних j-м напрямом досліджень, немає максимально можливих (100 балів) оцінок, а верхня — випадку, коли всі оцінки, одержані j-м напрямом досліджень, є максимально можливими. Важливість j-гo напрямку збільшується при зміні k100 j від 0 до 1. Цей показник слід розглядати як додатковий до основного показника важливості M j. Він характеризує значущість об’єкта i з точки зору кількості присуджених йому «перших місць».
Крім абсолютних величин оцінки важливості напрямку при обробці даних анкет опитування застосовуються також відносні показники. Для цього індивідуальні показники спочатку нормуються, а потім обчислюються середньозважені величини. Нормування – це перехід від абсолютних величин до відносних.
Середня вага кожного напрямку (нормована оцінка) розраховується за формулою:
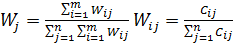(8.5)
Оскільки оцінки, поставлені кожним експертом окремим напрямкам різняться, як правило, значно, доцільно обчислювати розмах, використовуючи для цього залежність:
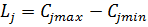(8.6)
де L – розмах оцінок, в балах, даних j-му напрямку;
C j m ax Cjm in – відповідно максимальна та мінімальна оцінки, поставлені j-му напрямку окремим експертом.
б) Показником рівня узгодженості думок експертів стосовно відносної важливості сукупності всіх запропонованих до оцінювання об’єктів слугує коефіцієнт конкордації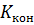 
. Його визначають для кожного питання на кшталт «оцінка важливості» шляхом обчислення таких показників:
— середньої арифметичної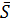 
сум рангів оцінок, одержаних усіма об’єктами:
(8.7)
де m — кількість об’єктів експертизи, i = 1, 2, …, m;
— відхилень d j суми рангів оцінок, одержаних об’єктом jвід середньої арифметичної сум рангів оцінок, одержаних усіма об’єктами:
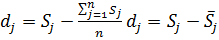(8.8)
— показників Т i однакових рангів оцінок, наданих i-м експертом. Якщо всі m рангів оцінок, наданих i-м експертом, різні, то T i = 0; якщо серед рангів оцінок трапляються однакові, тоді:
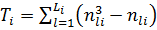(8.9)
де L i — кількість груп однакових рангів;
n lj — кількість об’єктів, які утворюють l-у групу однакових рангів.
Потім обчислюють коефіцієнт конкордації 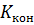за формулою:
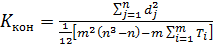(8.10)
Коефіцієнт конкордації приймає значення від 0 до 1. Чим більше значення коефіцієнта конкордації, тим вище ступінь узгодженості думок експертів. При Ккон = 1 є повна узгодженість думок експертів; якщо К = 0, то узгодженість практично відсутня.
Якщо значення коефіцієнта конкордації Ккон невелике, спостерігається незначна узгодженість поглядів експертів. Причини тут можуть бути різні: або в досліджуваній сукупності експертів справді немає спільності поглядів, або серед сукупності експертів існують групи з великою узгодженістю поглядів, однак їхні узагальнені думки протилежні.
Статистична істотність (довірча імовірність) коефіцієнта Ккон перевіряється за критерієм Пірсона χ2з (n – 1) ступенями свободи:
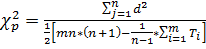(8.11)
Розраховане значення співставляється з табличним значенням для n-1 ступенів свободи та довірчої ймовірності (Р = 0,95або Р = 0,99). Якщо факт > табл., то коефіцієнт конкордації істотний, якщо навпаки то необхідно збільшити кількість експертів.
Рівень узгодженості поглядів кожного експерта з рештою експертів унаочнює багатокутник, кожна вершина якого відповідає певному експерту, а лінії, що з’єднують певну вершину з іншими, — коефіцієнтам парної рангової кореляції. Ступінь збігу думок двох експертів визначається за допомогою коефіцієнта парної рангової кореляції між оцінками двох будь-яких експертів α і βта інформаційної міри збігу думок (Устюжанінова).
Коефіцієнт парної рангової кореляції між оцінками двох будь-яких експертів α і β визначають за формулою:
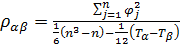, (8.12)
де 
— різниця (за модулем) величин рангів оцінок j-го напряму досліджень, заданою експертами а і β,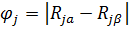 
;
T a , Tβ — показники однакових рангів оцінок експертів а і β.
Коефіцієнт парної рангової кореляції може набувати значення – 1 ≤ ρ ≤ +l. Значення ρ = + 1 відповідає цілковитій узгодженості поглядів двох експертів. Значення ρ= – 1 показує, що думка одного експерта є протилежною погляду іншого.
Інформаційна міра збігу думок (Устюжанінова) обчислюється за формулою:
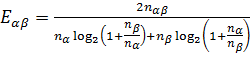, (8.13)
де Eαβ – міра збігу думок експертів α і β;
nαβ – кількість напрямків (факторів, параметрів), однаково оцінених
експертами αі β (по балам);
nα, nβ – кількість факторів, оцінених відповідно експертом α та експертом β
(якщо напрямок оцінено в 0 балів, то в кількість оцінених воно не
включається).
Багатокутник також дає змогу визначити групи експертів, усередині яких узгодженість поглядів велика, тоді як між групами існує неузгодженість.
Чим нижчий рівень статистичної значущості показника узгодженості поглядів експертів, тим більшою є імовірність існування невипадкової узгодженості поглядів експертів.
Розкид думок експертів, рівень якого по суті відображає узгодженість думок, оцінюється, окрім коефіцієнта конкордації, за допомогою інших статистичних показників, в тому числі:
1) дисперсія оцінок, даних j-му напрямку:
(8.14)
2) коефіцієнт варіації оцінок, даних j-ому напрямку:
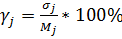, (8.15)
.
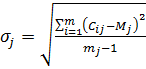3) загальна дисперсія оцінок:
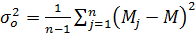, (8.16)
де
;
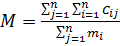4) загальна дисперсія рангів:
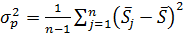, (8.17)
де
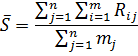
в) Показник активності експертів kаеi визначають таким чином:
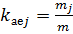, (8.18)
де kаеi– коефіцієнт активності експертів по j-му напрямку;
mj– кількість експертів, що оцінили j-й напрямок;
m – загальна кількість експертів.
Чим більше kаеi, тим більша кількість експертів вважають себе компетентними в оцінюванні i-го напряму досліджень.
г)Аналіз компетентності, як правило, здійснюють за допомогою спеціальних анкет. У відповідях на них кандидати в експерти мають продемонструвати свої ділові і фахові якості, а також аналітичні здібності.
Для визначення відповідності потенційного експерта названим вимогам використовують анкетне опитування. Додатково ще вдаються до самооцінювання компетентності експерта. Коли експерт визначає міру своєї обізнаності з досліджуваного питання. Оброблення даних дає можливість одержати кількісну оцінку компетентності потенційного експерта за такою формулою: ,
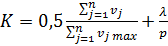, (8.19)
де v j — вага показника, закресленого експертом стосовно j -ї характеристики в анкеті у балах;
v j max — максимальна вага (межа шкали) j-ої характеристики в балах;
n — загальна кількість характеристик компетентності в анкеті;
λ— вага клітинки, закресленої експертом у шкалі самооцінки в балах;
р — межа шкали самооцінки експерта в балах.
Показником компетентності експерта може слугувати такий коефіцієнт:
, (8.20)
де kk — коефіцієнт компетентності експерта;
kз — коефіцієнт міри ознайомлення експерта з обговорюваною проблемою. Він визначається шляхом самооцінки експерта за десятибальною шкалою. Значення балів для самооцінки:
0 — експерт не розуміється на питанні;
1, 2, 3 — експерт мало розуміється на питанні, але воно належить до кола його інтересів;
4, 5, 6 — експерт задовільно розуміється на питанні, але не бере безпосередньої участі в практичному розв’язанні його;
7, 8, 9 — експерт добре розуміється на питанні, бере участь у практичному розв’язанні його;
10 — питання належить до кола вузької спеціалізації експерта.
Експерту пропонують самому оцінити міру обізнаності з питанням і підкреслити відповідний бал, який потім помножують на 0,1 і отримують коефіцієнт kз;
ka — коефіцієнт аргументації, який розраховують як суму балів еталонної таблиці. У цій таблиці експерт оцінює джерело інформації за градаціями: В (висока), С (середня), Н (низька).
Приклад 8.1.
Трьом експертам треба визначити рейтинг п’яти об’єктів інвестування. Кожен експерт оцінює міру привабливості інвестицій за балами від одного до п’яти. Оцінки експертів наведено в таблиці 8.1.
Таблиця 8.1 – Оцінки експертів
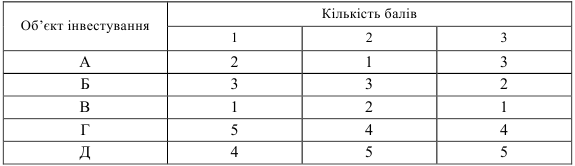
Потрібно встановити, чи є в наведених результатах певний порядок стосовно відносної привабливості сукупності запропонованих до оцінювання об’єктів інвестування і якщо є, тоді визначити їхні реальні рейтинги.
Розв’язок.Підрахуємо суму квадратів відхилень di2 та коефіцієнт конкордації .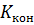
;
.
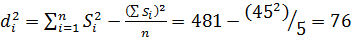Оскільки значенню di2= 76 відповідає рівень значущості а, що перебуває у межах (0,0053; 0,015), гіпотезу про неузгодженість думок експертів відхиляють з імовірністю похибки, яка не перевищує 0,015. Остаточно розташувати об’єкти за їхньою інвестиційною привабливістю можна, наприклад, за сумами номерів Si.
Так, напрямок А має посісти друге місце, напрямок Б слід поставити на третє, напрямок В — на перше місце, потім йдуть напрямки Г та Д.
8.2 Аналіз результатів опитування експертів
Завершальним етапом експертної оцінки є аналіз результатів опитування, які служать інформаційним та рекомендаційним матеріалом для прийняття управлінських рішень. Аналізу повинні підлягати не лише система статистичних оцінок, але й весь хід проведення експертизи: визначення цілей, підбір експертів, складання опитувальних анкет, організація проведення опитування. Всі етапи експертизи повинні бути ретельно проаналізовані, щоб виявити всі негативні моменти і виключити їх в майбутньому. Система статистичних характеристик, отриманих за результатами обробки статистичних анкет – це лише сукупність показників, «сировина», що потребує вмілого та професіонального осмислення, оцінки, тлумачення, від яких, в кінцевому результаті, залежить успіх та практична цінність всієї експертизи.
Методика проведення аналізу результатів опитування експертів залежить, по-перше, від виду експертизи – індивідуальної чи колективної, а по-друге, від напрямку експертизи – визначення часу здійснення певної події, оцінка очікуваних в майбутньому величин параметрів об'єктів (процесів, явищ); оцінка відносної важливості фактора (напрямку); оцінка питомої ваги різних видів рішень та ін.
Враховуючи певну обмеженість індивідуальних експертних оцінок, їх результати необхідно порівнювати з існуючими поглядами на досліджувану проблему та результатами прогнозних оцінок інших спеціалістів.
За результатами експертизи слід провести якісну оцінку кожного члена експертної групи. При цьому слід звернути увагу не тільки на визнання та популярність окремих спеціалістів, а і від їх відношення до справи: точності, добросовісності, акуратності, творчого підходу, переконаності в своїй правоті, що може бути аргументована.
Необхідно дотримуватися досить важливого правила: жоден із спеціалістів не повинен бути виключений з експертної групи за формальними правилами (наприклад, за показниками узгодженості думок) без зваженого аналізу суті питання. Історія науки та техніки неодноразово ілюструє факти, що, на перший погляд, парадоксальні ідеї та висновки містять в собі нові фундаментальні відкриття.
Багато експертів являються, як правило, видатними спеціалістами тільки в своїй області. Тому їх висновки слід розглядати в більш широкому контексті, наприклад, з перспективами розвитку економіки підприємства (регіону, країни).
Іншими словами, висновки експертів слід пов'язувати із зовнішніми факторами, що визначають майбутнє прогнозованого об'єкта. Не слід забувати, що існує своя «цехова» зацікавленість експертів, свої інтереси, які не завжди збігаються із загальними інтересами. В зв'язку з цим висновки експертів повинні бути детально перевірені, осмислені та творчо використані.
8.3 Експертні оцінки і моделі бінарного вибору
Уявлення про лінійну взаємодію – швидше абстракція, що допомагає спростити задачу, зробивши її завжди вирішуваною, але з деякою помилкою, якою можна нехтувати. Логіка отримання результатів по такій схемі оцінювання без урахування сумісних ефектів цілком з'ясовна. Рішення шукається для конкретної ситуації з фіксованою структурою показників, яка хоча і не указується в завданні експерту, але, як правило, присутня в його уявленнях про вирішувану задачу. Але як тільки структура починає змінюватися, зразу ж з'являються невраховані ефекти взаємодії і надійність експертних оцінок різко знижується. Тому безпосереднє оцінювання показників з передбачуваною лінійною структурою взаємозв'язків необхідно замінити складнішою, заснованою на модельному представленні структурою, але без ускладнення самої процедури опиту експертів. При цьому модель, що відображає взаємозв'язок між можливістю появи події, що цікавить нас, і набором оцінюваних показників, повинна бути, ймовірно, нелінійної і, крім того, економетричною, оскільки інтерес викликають не тільки механізм взаємодії, але і кількісна оцінка сили цієї взаємодії, а також бажання замінити повторні експертні опити прогнозними оцінками. Останнє особливо важливе. Саме цією можливістю не володіють раніше розглянуті методи.
Таким чином, значення висловлюваного тут підходу в тому, щоб експертну інформацію використовувати для побудови моделі, а не для отримання самих оцінок. Виникає природне питання: «Яким чином експертна інформація може використовуватися для цих цілей?» Видно, можна запропонувати декілька підходів, що забезпечують реалізацію обговорюваної тут ідеї. Наша пропозиція полягає в тому, щоб інтуїцію і знання експертів застосувати для формування спеціального набору даних псевдовибірки, по якій оцінюються коефіцієнти моделі, що має відмінність від безпосередніх експертних оцінок, багатопланове застосування: аналіз, оцінка значущості чинників, прогноз очікуваних подій і т.п. Природно, це значно розширює область практичного використовування експертних рішень.
Реалізація даного підходу припускає введення бінарної змінної з наступним значенням:
Вважатимемо, що значення цієї змінної, що характеризує появу події, що цікавить нас, залежить від оцінюваного нами набору показників х1, х 2, ..., хm, і існує безліч різних варіантів х1, х2, ..., хn цих наборів хi = (xi1, xi2,…, xim), відмінних один від одного всіма або деякими своїми компонентами (оцінюваними показниками). Передбачається, що у кожного експерта є уявлення про те, при реалізації яких варіантів очікувана подія матиме місце, а при реалізації яких – немає. Математично це припущення записується у вигляді залежності:
,
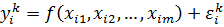де yik – очікуване значення бінарної залежної змінної, яке k-й експерт пов’язує з і-м набором оцінюваних показників;
f ( xi 1 , xi 2 ,…, xim ) – індексна функція, тобто функція, що приймає всього два значення: 0 і 1;
ε i k– помилка, яку може допустити k-й експерт, що оцінює вплив і-го набору на появу очікуваної події (ε i k– випадкова змінна із значеннями в номінальній шкалі: 1, 0, -1).
Тепер стає зрозумілою реалізація заснованої на модельному підході ідеї отримання експертних рішень. Спочатку в результаті цільового опиту експертів формується псевдовибірка, об'єднуюча в собі суб'єктивні думки з приводу закономірностей, що цікавлять нас, переваг, рейтингів, прогнозних оцінок і т.п. Потім за даними псевдовибірки будується регресійна залежність, що пов'язує суб'єктивні думки з одночасним їх усереднюванням в єдину формалізовану залежність. Побудована таким чином модель, по суті, є концентрованим виразом узагальненої думки експертів по проблемі, що вивчається, і може використовуватися для аналізу і отримання всіляких оцінок.
Модель як результат опиту, а не разові експертні оцінки є головною особливістю даного підходу. Завдяки цій особливості вдається одержати прогнозні оцінки експертних думок, тобто оцінки суб'єктивного характеру щодо тих подій або об'єктів, про яких експерти не знали або не мали уявлення у момент формування псевдовибірки.
Практична реалізація цієї процедури вимагає розгляду цілого ряду досить складних питань:
Як побудувати регресію на бінарну змінну?
Якими способами експерти повинні формувати вибіркову сукупність (псевдовибірку) для побудови регресії з бінарною залежною змінною?
Як оцінити компетентність експерта і адекватність побудованої таким чином моделі?
Як перевірити узгодженість думок опитуваної групи експертів?
Як оцінити надійність розрахункових характеристик, одержуваних за допомогою регресії суб'єктивних думок?
Яку змістовну інтерпретацію мають оцінки, одержані в результаті моделювання експертних переваг?
Чи можна, а якщо можна, то як використовувати статистичні методи для перевірки різного роду гіпотез, що висуваються щодо оцінюваних параметрів і об'єктів?
По суті, в цих питаннях немає нічого нового. Практично всі вони в тому або іншому ступені присутні в задачах прямого експертного оцінювання, забезпечуючи надійність одержуваних результатів. Але розрахунок і аналіз характеристик, а також відповідні висновки на їх основі в новому підході відрізняються від того, як це робиться в традиційному, тому вимагають спеціального розгляду.
8.4 Моделі множинного вибору в експертному оцінюванні майбутнього
Розглянемо випадок, коли перед експертами стоїть задача вибору не серед двох, а серед цілої безлічі альтернативних варіантів. За наслідками їх вибору, оформленим у вигляді псевдовибірки, вимагається побудувати модель, за допомогою якої можна буде здійснювати прогнозні розрахунки експертних переваг у вигляді відповідної вірогідності. Для вирішення цієї задачі можна скористатися мультіноміальноюлогіт-моделью, яка по суті є узагальненням логіт-моделібінарного вибору. Нижче достатньо детально описується мультіноміальналогіт-модельі деякі деталі, що характеризують особливість її побудови і аналізу.
Вірогідність настання того або іншого варіанту описується поліноміальною логіт-моделю
.
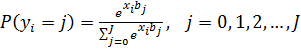Вектор незалежних змінних х = [ z j , wj ] складений з двох підвекторів, кожний з яких має власне смислове навантаження. Компоненти вектора z; прийнято називати атрибутами і розуміти їх як показники, по яких розрізняються альтернативи. У свою чергу, компоненти вектора wіназивають характеристиками.
Оцінка параметрів моделі не даєоднозначного результату, оскільки разом з обчисленими коефіцієнтами bідентична вірогідність дозволяє одержати вектор b + d. Уникнути цієї неоднозначності дозволяє операція нормалізації (стандартизації), значення якої в тому, щоб для одного з варіантів покласти bj = 0. Тоді оцінюється не J + 1 функція, а Jфункцій одного вигляду
,
після чого визначається ще одна функція через значення цих функцій шляхом віднімання їх суми з одиниці:
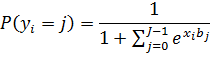
Це одна з особливостей побудови поліноміальної логіт-моделі.
Оцінювання коефіцієнтів моделі здійснюється шляхом чисельного рішення рівнянь правдоподібності. Для запису самого рівняння правдоподібності, а точніше його логарифмічної форми, зручно ввести змінну dij, яка приймає значення 1, якщо в i-м спостереженні (i-м індивідуумом) був вибраний j-й альтернативний варіант серед (J + 1)-го, і 0 – інакше. Тоді для кожного і тільки одне з dij буде рівне 1.
Використовуючи введену змінну dij, запишемо функцію логарифмічної правдоподібності
.
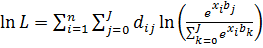Диференціюючи цей вираз по bj, одержимо систему рівнянь максимальної правдоподібності
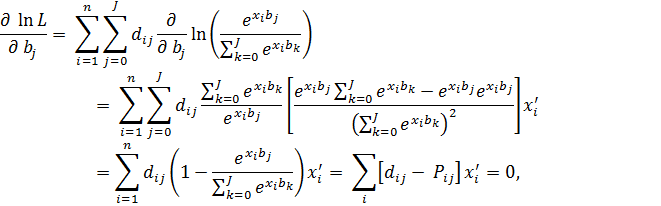
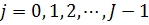
Рішення цієї системи з урахуванням того, що bj =0, здійснюється чисельно за допомогою методу Ньютона – Рафсона. Комп'ютерна реалізація влаштована таким чином, і про це вже мовилося, що нульові значення одержують параметри тієї моделі, яка відповідає останній з вказаних альтернатив. Іншими словами, якби ми захотіли, щоб b0 = 0, а не bj, то дані, відповідні альтернативі з номером j = 0, повинні бути введені останніми.
Для реалізації методу Ньютона – Рафсона потрібен матриця приватних похідних другого порядку. Крім того, за допомогою цієї матриці визначаються характеристики надійності самої моделі. Тому має сенс виписати цю матрицю в загальному вигляді:
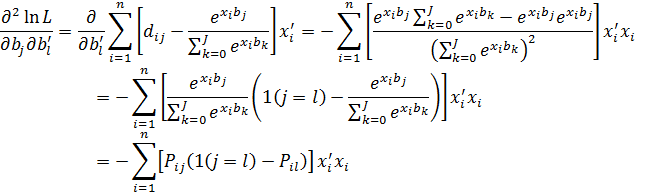
У одержаному виразі 1(j = l) приймає значення 1 при j = l і 0 – інакше. Це дозволяє здійснювати селекцію, оскільки результатом твору РЛ(j = l) є Р.,
Коефіцієнти моделі важко інтерпретуються. Нелінійний характер не дозволяє безпосередньо через коефіцієнти прослідити зв'язок між рівнем вірогідності і атрибутами (чинниками). Тому природно для цих цілей використовувати граничний аналіз. Диференціюючи по l-му атрибуту в i-й точціj-ю вірогідність, одержуємо граничний ефект у вигляді
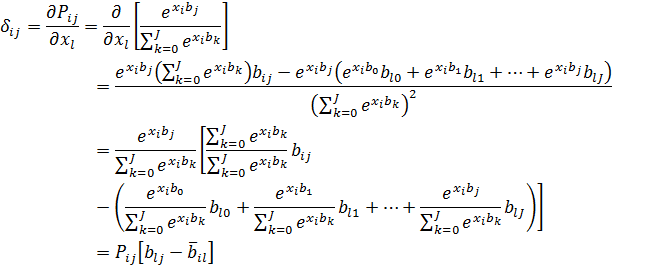
Дата: 2018-12-21, просмотров: 246.
