Анотація

Лінійне рівняння регресії. Прогнозування в умовах невизначеності: тест рекурсивної оцінки коефіцієнтів регресії; тест рекурсивної оцінки значень Y; тест рекурсивної оцінки помилок регресії. Застосування матриць до моделі лінійної регресії.

5.1 Лінійне рівняння регресії

Припустимо, що члени ряду Y₁, Y₂, ..., Y_n є реалізацією взаємно незалежних ідентичних нормальних випадкових величин, і члени ряду представлені нормальними випадковими величинами. Найбільш проста модель при цьому вийде, якщо припустити, що члени ряду мають одне й те ж стандартне відхилення, рівне σ, але відрізняються значеннями своїх математичних сподівань E(Yi). Зазвичай припускається, що E(Y) залежить від деякої величини X. Якщо ця залежність лінійна, то модель називається моделлю [парної] лінійної регресії. Коефіцієнти лінійного рівняння регресії приймаються за наближені значення коефіцієнтів моделі. У такому випадку:

                                                            (5.1)

де і = 1, 2, ..., n;

β₁, β₂– не залежитьвід і, тобто являються константами моделі.

Ми отримаємо інше, більш поширене визначення моделі [парної] лінійної регресії, якщо зауважимо, що будь-яка випадкова величина Y з математичним очікуванням μ і стандартним відхиленням σ може бути представлена як Y = μ + ε, де випадкова величина ε має математичне сподівання, рівне нулю , і стандартне відхилення σ_ε = σ.

Отже, статистична модель

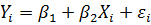,                                                         (5.2)

де і = 1, 2,..., n;

Y_i – випадкова величина;

X_i - константа;

ε₁, ε₂, ..., ε_n – нормальнівипадкові величиниз одним і тим же математичним сподіванням, рівним 0, та стандартним відхиленням σ;

β₁, β₂ – константи моделі, що не залежатьвід і, називається моделлю [парної] лінійної регресії.

Параметри β₁, β₂ називаються коефіцієнтами регресії. Випадкові величини ε₁, ε₂, ..., ε_n називаються випадковими членами або помилками. Присутність випадкових членів в моделі означає, що залежність між Y і X не є строго лінійною. Ми також додатково припустимо, що ε₁, ε₂, ..., ε_n є взаємно незалежними випадковими величинами. Причому X називається регресором, а Y - залежною змінною. Коли ми говоримо, що X_i - константа, то мається на увазі, що вона є такою при фіксованому і, а при різних і X може приймати різні значення. Ми розглядаємо Y_i як випадкову величину для фіксованого i. Якщо i ≠ j, то Y_i і Y_jбудуть різними випадковими величинами з різними математичними очікуваннями, рівними β₁ + β₂Х_i і β₁ + β₂Х_j відповідно, хоча і з однаковими стандартними відхиленнями, рівними σ.

Важливо відзначити, що в моделі (5.2) коефіцієнт β₂ дорівнює середньому зміни в Y при збільшенні X на одиницю. Дійсно,

,

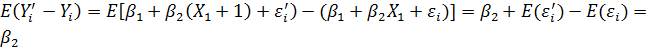де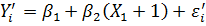

У прогнозуванні звичайно передбачається, що і = 1, 2, ..., n відповідають моментам часу, які мають однаковий крок (місяць, квартал і т.д.). Допускається, щоб деякі значення ібули відсутні. Не обов'язково також, щоб перше значення дорівнювало 1. Давайте розглянемо декілька прикладів.

1. Ми отримаємо модель, лінійно залежну від часу, якщо візьмемо X_i= і:

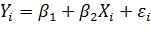, де і = 1, 2, … , n.

2. Якщо X_i = і², то залежність Y від часу буде квадратичною:

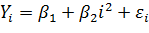, де і = 1, 2, … , n.

3. Якщо припустити, що Х_i = Ln (і), то виходить логарифмічна модель:

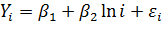, де і = 1, 2, … , n.

4. Розглянемо наступну модель, яку називають моделлю постійної еластичності:

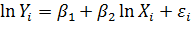, де і = 1, 2, … , n.

Вона буде еквівалентна моделі:

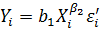, де і = 1, 2, … , n.

5. 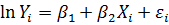–модель при X_i = і еквівалентна моделі постійного зростання 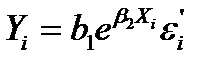з тим же застереженням щодо випадкового члена ε_i, що і в попередній моделі.

5.2 Прогнозування в умовах невизначеності: тест рекурсивної оцінки коефіцієнтів регресії; тест рекурсивної оцінки значень Y; тест рекурсивної оцінки помилок регресії

Тест рекурсивної оцінки коефіцієнтів регресії тісно пов'язаний з уже знайомою нам концепцією expost прогнозування. Ідея тесту полягає в побудові expost 95%-них довірчих інтервалів для коефіцієнтів β₁ і β₂. Для цього спочатку задають число k, за умови, що 0 < k < n. Зазвичай розглядають невеликі значення k, щоб можна було простежити динаміку зміни коефіцієнтів b₁ і b₂ на досить великому інтервалі. Потім для перших k даних знаходять коефіцієнти рівняння регресії b₁^(k) і b₂^(k) і відповідні 95%-ні довірчі інтервали для β₁ і β₂. Процедура повторюється для k + 1, k + 2 і т.д., аж до n. Динаміка зміни b₂ і відповідних 95%-них довірчих інтервалів для β₂ показана на рис. 5.1.

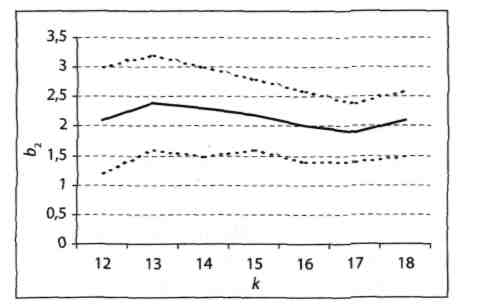
Рисунок 5.1 - Динаміка змін коефіцієнта b₂ і відповідних 95%-них довірчих інтервалів для β₂

Примітка. Середня лінія відповідає рекурсивним значенням b₂, а пунктирні лінії позначають верхні та нижні межі відповідних довірчих інтервалів.

Для кожного значення k (12 ≤ k ≤ 18) відповідний 95%-ний інтервал з центром в b₂^(k) з імовірністю 95% містить параметр β₂. Так як β₂ є параметром моделі і не залежить від k, то той факт, що смуга на рис. 5.1 не має поступального руху вгору або вниз, а робить коливальні рухи навколо деякого числа, вказує на те, що процес, як видно, слідує моделі лінійної регресії.

Тест рекурсивної оцінки значень Y заснований на формулі:

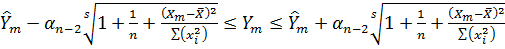,  (5.3)

яку використовують при побудові 95%-них інтервалів прогнозу для значень Y. Він дає досить чітке уявлення про те, наскільки даний процес слідує моделі лінійної регресії. Тут, як і в попередньому тесті, ми задаємо число k в діапазоні 0 <k < n і потім за допомогою формули (5.3) визначаємо 95%-ний інтервал прогнозу Δ_{к +1} для Y_{k +1}, при заданих значеннях пар даних (X₁, Y₁), (X₂, Y₂),..., (X_k, Y_k). Нагадаємо, що серединою інтервалу Δ_{к +1} є expost прогноз. Випадкова величина Y_{k +1} з ймовірністю 95% повинна опинитися в інтервалі Δ_{к +1}. Потім ми додаємо пару даних (X_k+l, Y_k+l) і повторюємо всю процедуру для k + 1 пар даних (X₁, Y₁), (X₂, Y₂),..., (X_k+1, Y_k+1) і т.д. В результаті ми отримаємо рекурсивні інтервали Δ_k+1, Δ_k+2, ..., Δ_n. Серединою кожного такого інтервалу Δ_i буде значення expost прогнозу. Відповідні 95%-ні рекурсивні інтервали прогнозу для значень Y наведені на рис. 5.2.

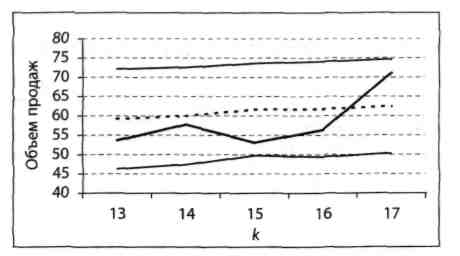
Рисунок 5.2 - 95%-і рекурсивні інтервали прогнозу для значень Y

Примітка. Окреслена напівжирним лінія в середині смуги відповідає даним за останні 5 кварталів.

Пунктирна лінія на рис. 5.2 показує значення expost прогнозів. І хоча вихідні дані з ними не збігаються, вони потрапляють в смугу, задану відповідними 95%-ними рекурсивними інтервалами прогнозу. Цей тест підтверджує висновок, отриманий в результаті розглянутого раніше тесту рекурсивної оцінки коефіцієнтів регресії, про те, що дані, можливо, слідують моделі лінійної регресії.

Зазвичай замість тесту рекурсивної оцінки значень Y, який ми тільки що вивчили, розглядається еквівалентний йому тест рекурсивної оцінки помилок регресії. Якщо ми позначимо довжину 95%-ного рекурсивного інтервалу прогнозу Δ_k як 2L_k, то формула (5.3) може бути записана в наступному вигляді:

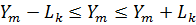.                                 (5.4)

Нерівність (5.4) еквівалентна твердженню, що помилкаехpost прогнозування зймовірністю 95% повинназнаходитись в інтервалі: .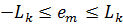

Як іу вище описаних тестах, тут задають число k в діапазоні 0 < k < n, а потім послідовно знаходять 95%-ніінтервали прогнозу [-L_k+1; L_k+1], [–L_k+2; L_k+2], ..., [-L_n; L_n] для помилок е_k+1, e_k+2, ..., е_n. На рис. 5.3 представлені результати тесту рекурсивної оцінки помилок регресії.

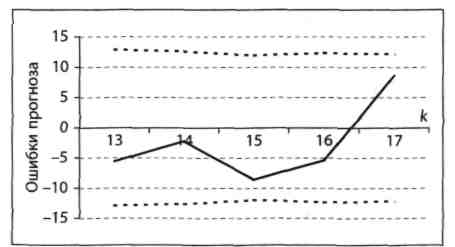
Рисунок 5.3 – Помилки expost прогнозів і відповідні 95%-ні рекурсивні інтервали прогнозу для помилок е

На рис. 5.3 дві пунктирні лінії, розташовані симетрично відносно горизонтальної осі, представляють границі 95%-них рекурсивних інтервалів прогнозу для помилок е_і. Самі помилки представлені лінією між ними. Хоча значення помилок і не виходять за межі смуги, прогнозист може вирішити, що вони занадто великі.

У більшості випадків вони складають більше 10% від відповідних значень Y. Він може вирішити, що для отримання більш точного прогнозу потрібно врахувати вплив економічних та інших умов.

5.3 Застосування матриць до моделі лінійної регресії

Детермінований матричний предиктор має сенс будувати в тих ситуаціях, коли можливість застосування статистичних методів моделювання повністю виключена. Прикладом може служити ситуація, в якій дослідник володіє всього двома, трьома спостереженнями. Щоб перейти до формального опису моделі з таким предиктором, введемо позначення:

Х_ti – величина i-го показника у момент часу t;

X_t-1i– величина i-го показника у момент часу t-1;

D х_ti – величина зміни (приросту) i-го показника.

Далі природно припустити, що будь-яка зміна довільного i-го показника залежить від величини решти показників. Це може бути функціональна або регресійна залежність. Розглянемо випадок, коли малий об'єм ретроспективних даних не дозволяє реалізувати відомі методи ідентифікації цієї залежності. Єдино доступною альтернативою ідентифікації в подібній ситуації є підхід, заснований на значному спрощенні цієї залежності. В якості такої спрощеної форми зручно використовувати лінійне представлення приростів. Відразу помітимо, що модель, побудована за двома спостереженнями, не може претендувати на застосування для розрахунків, поширюваних за рамки, обкреслені короткостроковими прогнозами. Тому при розгляді короткострокових періодів таке спрощення не приводить до значного зростання помилки прогнозування навіть у тому випадку, коли істинна залежність явно нелінійна.

Модель цієї простої (лінійної) залежності будується в припущенні, що приріст будь-якого з показників формується під впливом всіх остаточних, будучи як би сумарною величиною, причому кожен показник окремо робить незначний вплив, і серед них немає домінуючих. Для реалізації цього припущення вводиться в розгляд характеристика, що встановлює ступінь впливу j-гo показника на зміни, що відбуваються в і-му. В якості такої характеристики зручно використовувати непрямий темп приросту

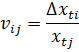
Якщо умовитися, що на формування приросту всі показники надають рівномірну дію, то, розділивши n_ij на (n–1), одержимо ту частку в прирості i-го показника, яка сформована під впливом j-го. Використання введеної міри ступеня впливу j-го показника на i-й дозволяє виразити приріст Dх_t через суму добутків

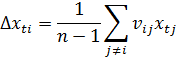
Враховуючи, що Dх_ti = x_ti – x_t–1 можна величину будь-якого і-го показника представити у вигляді суми попереднього значення x_ti і приросту Dх_ti:

.

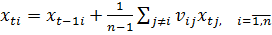Для одержаної системи рівнянь (5.3), ввівши позначення

.

можна використовувати компактний матричний запис

.

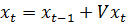Вважаючи, що невідомим вектором в цій системі є х_t, запишемо його таким чином:

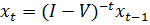,                                      (5.5)

де через I позначена одинична матриця.

Зворотну матрицю (I–V)^-1 називатимемо матричним предиктором. Він визначає перехід із стану, описуваного вектором значень попереднього моменту часу, в стан, представлений вектором значень теперішнього моменту часу. Позадіагональні елементи зворотної матриці інтерпретуються як непрямі темпи зростання рівномірно розподілених частин прогнозованих показників, а діагональні – як прямі темпи зростання частини, що залишилася.

У припущенні, що матричний предиктор перспективного періоду майже не відрізняється від матричного мультиплікатора поточного періоду, вираз (5.5) дозволяє розраховувати прогнозні оцінки. Основна перевага даного підходу полягає у тому, що з його допомогою можна проводити розрахунки для багатовимірних рядів динаміки навіть у тому випадку, коли дослідник має в своєму розпорядженні спостереження лише за два періоди. Правда, статистична надійність таких прогнозних розрахунків не перевіряється і спирається, в основному, на ту обставину, що навіть при зміні характеру динаміки прогнозованих процесів структура самого предиктора, як правило, змінюється трохи. Як показує практика прогнозних розрахунків, застосування цієї моделі переважно звичних розрахунків з використанням темпів зростання, в яких зовсім не враховується взаємодія між модельованими показниками.