Анотація
Поняття оптимального прогнозу. Оцінювання адекватності прогнозованої моделі. Критерії визначення якісного прогнозу. Оцінка точності прогнозованої моделі та прогнозів.
9.1. Поняття оптимального прогнозу
Оптимальний прогноз — це зроблене на підставі економічної теорії передбачення, яке використовує всю доступну на момент побудови прогнозу інформацію. Для оптимального прогнозу граничний виграш та граничні витрати збігаються.
Оптимальний прогноз іще називають прогнозом раціональних сподівань. Раціональні сподівання можуть відрізнятися від фактичних значень, але будь-яка різниця має бути випадковою й непередбачуваною. Оскільки раціональні сподівання ґрунтуються на коректній економічній теорії, вони мають властивості незсуненості (за умови квадратичної функції витрат) та ефективності.
Незсуненість означає, що помилка прогнозу має нульове математичне сподівання.
Ефективність передбачає, що в процесі прогнозування буде використана вся доступна інформація, отже, помилка прогнозу не буде корелювати з цією інформацією.
Існують численні критерії перевірки раціональності послідовності прогнозів. Стандартний критерій незсуненості потребує перевірки гіпотези стосовно того, що α= 0 та β = 1 водночас для такої моделі:
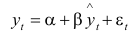, (9.1)
де yt — ряд фактичних значень або спостережень;
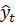— ряд прогнозованих значень;
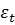— випадкові залишки.
Перевірка ефективності є складнішою оскільки неможливо коректно визначити відповідний масив інформації, стосовно якого похибки прогнозу будуть некорельованими.
Узагальнюючи огляд критеріїв визначення якісного прогнозу, можна стверджувати, що варто користуватися системою критеріїв, які мають враховувати:
ü кількість зусиль, витрачених на побудову моделі, і наявність готових комп’ютерних програм;
ü швидкість, із якою метод уловлює істотні зміни у поведінці ряду, наприклад раптовий зсув математичного сподівання або збільшення кута нахилу лінії тренду;
ü існування серійної кореляції у помилках;
ü незмінюваність первинних даних;
ü повний обсяг роботи в деяких сферах діяльності — тисячі рядів щомісяця потребують оновлення, невеликі витрати й швидкість мають першорядне значення;
терміновість прогнозування.
9.2. Оцінювання адекватності прогнозованої моделі.
Незалежно від виду і способу побудови економіко-математичної моделі питання про можливість її застосування з метою аналізу і прогнозу економічного явища може бути вирішено тільки після встановлення адекватності моделі. Оскільки повної відповідності моделі реальному процесу або об’єкту бути не може, адекватність певною мірою умовне поняття. При моделюванні мається на увазі адекватність не взагалі, а тим властивостям моделі, які вважаються суттєвими для дослідження.
Модель згладжування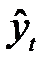 
певного часового ряду 
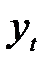вважається адекватною, якщо правильно відображає систематичні компоненти часового ряду. Ця вимога еквівалентна вимозі, щоб залишкова компонента 
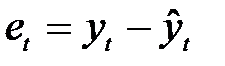(t = 1, 2, ..., n) відповідала таким властивостям випадкової компоненти часового ряду як: випадковість коливань рівнів залишкової послідовності, відповідність розподілу випадкової компоненти нормальному закону, рівність математичного сподівання випадкової компоненти нулю, незалежність значень рівнів випадкової компоненти. Розглянемо, яким чином здійснюється перевірка цих властивостей залишкової послідовності.
Перевірка випадковості коливань рівнів залишкової послідовності означає перевірку гіпотези про правильність вибору виду тренду. Для дослідження випадковості відхилень від тренду розраховують набір різниць 
(t = 1, 2, ..., n). Характер цих відхилень вивчається за допомогою ряду непараметричних критеріїв. Одним з таких критеріїв є «критерій серій», який використовує медіану вибірки, критерій «зростаючих» та «спадних» серій тощо.
Згідно з критерієм серій ряд із величин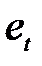 
розташовують у порядку зростання їхніх значень і знаходять медіану 
одержаного варіаційного ряду, тобто значення, що перебуває в середині для непарного п або середню арифметичну з двох середніх значень для п парного. Повертаючись до вхідної послідовності 
і порівнюючи значення цієї послідовності з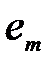 
, ставлять знак «плюс», якщо значення 
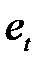, перевищує медіану, і знак «мінус», якщо воно менше за медіану; у випадку однаковості порівнюваних величин відповідне значення 
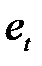пропускають. Отже, одержують послідовність, що складається із плюсів та мінусів, загальна кількість яких не перевищує п. Послідовність розташованих одне за одним плюсів або мінусів називають серією. Щоб послідовність 
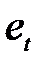була випадковою вибіркою, довжина найдовшої серії не має бути занадто великою, а загальна кількість серій – занадто малою.
Позначимо довжину найдовшої серії через Кmax, а загальну кількість серій – через v. Вибірка вважається випадковою, якщо виконуються такі нерівності для 5 %-го рівня значущості:
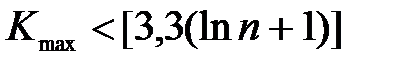, (9.2)
,
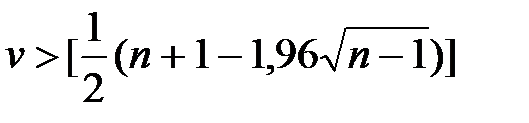де квадратні дужки означають цілу частину числа.
Якщо хоча б принаймні одна з цих нерівностей порушується, то гіпотеза про випадковий характер відхилень рівнів часового ряду від тренду спростовується, а модель тренду визнається неадекватною.
Перевірка відповідності розподілу випадкової компоненти нормальному закону розподілу може бути зроблена лише наближено за допомогою дослідження показників асиметрії (А) і ексцесу (Е), оскільки часові ряди, як правило, не дуже довгі. При нормальному розподілі показники асиметрії і ексцесу певної генеральної сукупності дорівнюють нулю. Припустимо, що відхилення від тренду являють собою вибірку з генеральної сукупності, тому можна визначити тільки вибіркові характеристики асиметрії й ексцесу та їхні помилки:
; 
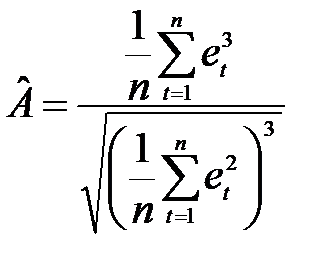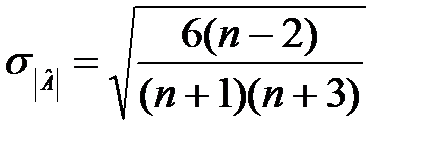; (9.3)
; 
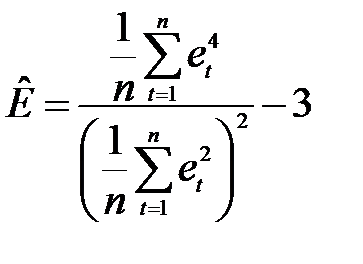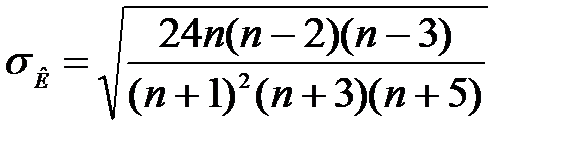, (9.4)
де 
– вибіркова характеристика асиметрії;
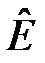– вибіркова характеристика ексцесу;
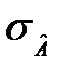і 
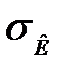– відповідні середньоквадратичні помилки.
Якщо одночасно виконуються такі нерівності:
; 
,
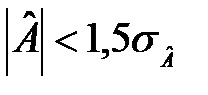то гіпотеза про нормальний характер розподілу випадкової компоненти приймається.
Якщо виконується хоча б одна з цих нерівностей:
; 
,
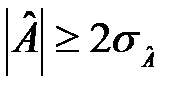то гіпотеза про нормальний характер розподілу відхиляється, трендова модель визнається неадекватною. Інші випадки потребують додаткової перевірки за допомогою складніших критеріїв. Для адекватних моделей доцільно ставити запитання щодо оцінювання їхньої точності. Вважається, що моделі з меншою розбіжністю між фактичними й розрахунковими значеннями краще відображають досліджуваний процес у майбутньому. Для характеристики рівня близькості використовують такі описові статистики:
середнє квадратичне відхилення (або дисперсія)
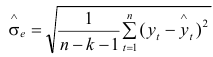; (9.5)
середню відносну похибку апроксимації (чим ближче до 0, тим точніша модель):
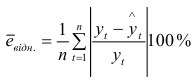; (9.6)
коефіцієнт сходження:
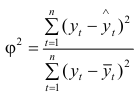, (9.7)
коефіцієнт детермінації (чим ближче до 1, тим точніша модель):
. (9.8)
У формулах (9.5—9.8) n — кількість рівнів ряду, k — кількість пояснювальних змінних у моделі, 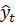— оцінки рівнів ряду за моделлю, 
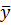— середнє арифметичне значення вибірки.
На підставі розглянутих показників можна з кількох адекватних моделей обрати найточнішу. Помилка прогнозу, обчисленого для періоду, характеристики котрого вже були використані при оцінюванні параметрів моделі, як правило, буде незначною та мало залежатиме від теоретичної обґрунтованості, застосованої для побудови моделі.
Оскільки формально-статистичний вибір кращої моделі в багатьох випадках не гарантує цілковитої впевненості в його правильності, адже добрий прогноз можна отримати і на підставі поганої моделі, і навпаки, тому про якість застосовуваних методик і моделей у прогнозуванні можна судити лише за сукупністю зіставлень прогнозів і їх реалізації. При цьому незалежно від обраної методики та моделі прогнозування джерелами помилок прогнозу можуть бути:
1) природа змінних (випадковий характер змінних гарантує, що прогноз відхилятиметься від справжніх величин, навіть якщо модель правильно специфікована, її параметри точно відомі);
2) природа моделі (сам процес оцінювання спричиняє похибки оцінок параметрів);
3) помилки, привнесені прогнозом незалежних випадкових величин (пояснювальних змінних);
4) помилки специфікації моделі.
Перевірка рівності математичного сподівання випадкової компоненти нулю, якщо вона розподілена за нормальним законом, виконується на основі t-критерію Стьюдента. Розрахункове значення цього критерію задається формулою
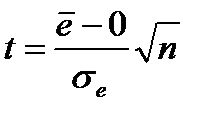, (9.9)
де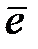 
– середнє арифметичне значення рівнів залишкової послідовності 
;
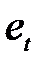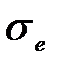– стандартне (середньоквадратичне) відхилення для цієї послідовності.
Якщо розрахункове значення t менше табличного значення tα статистики Стьюдента із заданим рівнем значущості α і числом ступенів свободи п – 1, то гіпотеза про рівність нулю математичного сподівання випадкової послідовності приймається, в протилежному випадку ця гіпотеза відхиляється і модель вважається неадекватною.
Перевірка незалежності значень рівнів випадкової компоненти, тобто перевірка відсутності суттєвої автокореляції в залишковій послідовності, може здійснюватися за рядом критеріїв, найбільш поширеним з яких є DW-критерій Дарбіна-Уотсона. Зазначимо, що розрахункове значення критерію Дарбіна-Уотсона в інтервалі від 2 до 4 свідчать про від’ємний зв’язок. У цьому випадку його треба перетворити за формулою DW' = 4 – DW і далі використовувати значення DW'.
Висновок про адекватність трендової моделі робиться, якщо всі розглянуті вище чотири перевірки властивостей залишкової послідовності дають позитивний результат.
9.3. Критерії визначення якісного прогнозу
Якість прогнозу характеризують такі поширені в прогностичній літературі терміни, як точність і надійність. Проте зміст цих термінів часто тлумачать досить неоднозначно. Це можна пояснити тим, що нині поки не знайдено ефективного підходу до оцінювання якості прогнозу, окрім його практичного підтвердження.
Про точність прогнозу прийнято судити за розміром помилки прогнозу — різниці між прогнозовим і фактичним значенням досліджуваного показника. Але такий підхід можливий лише тоді, якщо дослідник має інформацію стосовно справжніх значень часового ряду, який він оцінював під час розроблення прогнозів. Наприклад, період випередження вже завершився, і дослідник має фактичні значення змінної (це можливо в разі короткотермінового прогнозування) або прогноз перебуває в стадії розроблення, тобто прогнозування здійснюється для певного моменту часу в минулому, для якого існують фактичні дані. Спрощену схему періодів прогнозування показано на рис. 9.1.
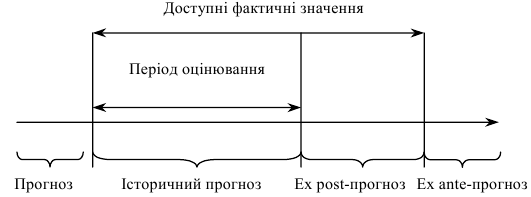
Рис. 9.1 – Спрощена схема періодів прогнозування
В останньому випадку йдеться про використання expost-прогнозу. Його сутність полягає у побудові моделі за меншим обсягом даних (n - m) із подальшим порівнянням прогнозовихоцінок за останніми m точками (для t від n - m + 1 до n) із відомими фактичними, але спеціально залишеними рівнями ряду. Отримані ретроспективно помилки прогнозу певною мірою характеризують точність застосовуваної методики прогнозування й можуть виявитися корисними в зіставленні кількох прогнозів.
Розмір помилки ретроспективного прогнозу не можна розглядати як остаточний доказ придатності, або навпаки, непридатності застосовуваного методу прогнозування. До неї варто ставитися з відомою обережністю і при її застосуванні в якості міри точності необхідно враховувати, що вона отримана при використанні лише частини наявних даних. Проте ця міра точності має більшу наочність і теоретично більш надійна, ніж похибка прогнозу, обчислена для періоду характеристики котрого вже були використані при оцінюванні параметрів моделі.
На основі розглянутих показників можна зробити вибір з декількох адекватних моделей найбільш точної. Помилка прогнозу, обчислена для періоду, характеристики котрого вже були використані при оцінюванні параметрів моделі, як правило, будуть незначними і мало залежатимуть від теоретичної обґрунтованості, застосованої для побудови моделі.
Оскільки формально-статистичний вибір кращої моделі у багатьох випадках не дає повної впевненості у його правильності: гарний прогноз може бути отриманий і по поганій моделі, і навпаки, то, про якість прогнозів застосовуваних методик і моделей можна судити лише по сукупності зіставлень прогнозів і їхньої реалізації. При цьому незалежно від обраної методики моделі прогнозування джерелами помилок прогнозу можуть бути:
1) природа змінних (випадковий характер змінних гарантує, що прогноз буде відхилятися від справжніх величин, навіть якщо модель правильно специфікована та її параметри точно відомі);
2) природа моделі (сам процес оцінювання спричиняє похибки оцінок параметрів);
3) помилки, що вносяться прогнозом незалежних випадкових величин (пояснюючих змінних);
4) помилки специфікації моделі.
9.4. Оцінка точності прогнозної моделі та прогнозів
Параметричні методи аналізу точності прогнозів. За результатами ex post-прогнозу розраховують такі показники точності прогнозів за m кроків:
Середня квадратична похибка:
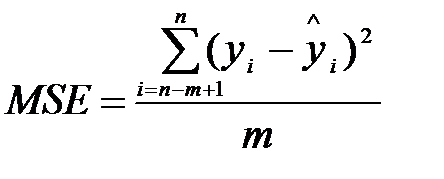, (9.10)
корінь із середньоквадратичної похибки
, (9.11)
середня абсолютна похибка:
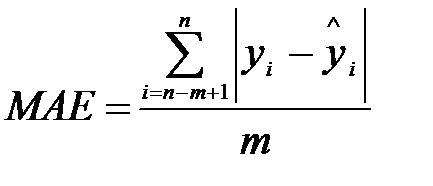, (9.12)
корінь із середньоквадратичної похибки у відсотках:
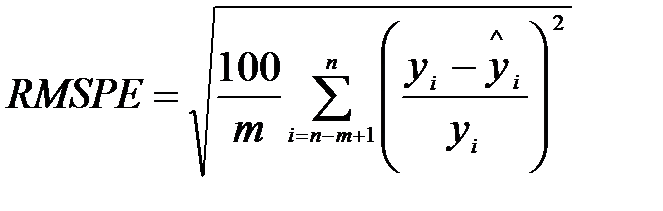, (9.13)
середня абсолютна похибка у відсотках (МАРЕ):
, (9.14)
Чим менше значення цих величин, тим вища якість ретропрогнозу. На практиці ці характеристики використовують досить часто. Даний підхід дає гарні результати, якщо на періоді ретропрогнозу не виникають принципово нові закономірності. На підставі останніх двох критеріїв можна дійти висновку стосовно загального рівня адекватності моделі шляхом їх порівняння. Цей рівень наведений у таблиці 9.1
Таблиця 9.1 – Точність пронозу в залежності від MAPE, RMSE
| MAPE, RMSE | Точність прогнозу |
| Менше 10% | Висока |
| 10% - 20% | Добра |
| 20% - 40% | Задовільна |
| 40% - 50% | Погана |
| Більше 50% | Незадовільна |
Вадою обговорених вище характеристик точності прогнозів є їх залежність від обраних одиниць виміру. Було б корисним указати безрозмірний показник, аналогічний до коефіцієнта кореляції. Одним з таких показників є коефіцієнт невідповідності Тейла, чисельником якого є середньоквадратична похибка прогнозу, а знаменник дорівнює квадратному кореню із середнього квадрата фактичних та оцінних значень:
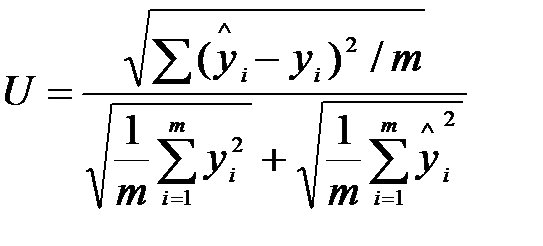, (9.15)
Перевага коефіцієнта Тейла полягає в тому, що його значення завжди перебувають у межах від нуля до одиниці. Якщо всі прогнози абсолютно точні, то U = 0. Якщо всі прогнози дорівнюють нулю, а жодне з фактичних значень не дорівнює нулю або навпаки, U дорівнюватиме одиниці. Таким чином, мале значення U засвідчує, що прогноз є точним, але максимального значення не існує. Значення, яке дорівнює одиниці, відповідає ситуації, коли всі прогнозові значення дорівнюють нулю, що нереально під час прогнозування номінальних величин, але під час розгляду змін такий прогноз відповідає моделі «без змін». Більші за одиницю значення вказують на те, що прогноз гірший, ніж прогноз «без змін».
Коефіцієнт невідповідності Тейла (U) може бути розкладений на три частини:
пропорцію зсунення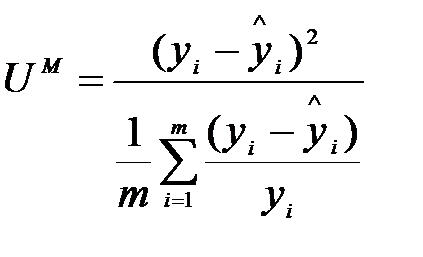 
, (9.16)
пропорцію дисперсії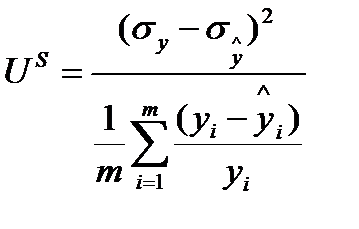 
, (9.17)
пропорцію коваріації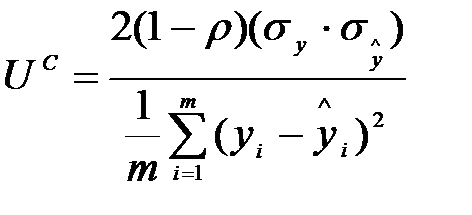 
, (9.18)
Зазначимо, що UM + US + UC = 1. Критерій зсуву пропорції (UM) використовується, щоб перевірити, чи є систематичне відхилення середніх розрахованих та фактичних рядів, тобто чи дає модель систематично завищені або занижені прогнози. Чим менше значення, тим краще. Якщо UM дорівнює нулю, у розрахованих (прогнозних) значеннях немає зсунень, тобто з моделлю все гаразд. Пропорція дисперсії (US) використовується, щоб переконатися, що модель має достатні динамічні властивості для відтворення дисперсії фактичних рядів. Наприклад, модель може відтворювати систематично менші коливання, ніж фактичні. Як і у випадку критерію UM, менше значення US вказує на менше зсунення. Пропорція коваріації вказує, як корелюють фактичні та розраховані ряди. Якщо UC дорівнює 1, то фактичні та розраховані ряди корелюють ідеально.
Критичні точки важливі як критерії якості, оскільки деякі моделі можуть бути точними, але погано передбачати зміни тенденції (наприклад, поворотні точки в циклах), тобто погано відтворювати критичні точки. Інші моделі можуть бути неточними, але мати гарний динамічний характер. Загалом може бути певний компроміс між точністю та динамічними властивостями моделі. Формального тесту для оцінки цієї властивості не існує. Проте візуальний огляд розрахованих та фактичних рядів звичайно одразу виявляє, здатна модель відтворювати критичні точки чи ні.
Обговорені характеристики точності прогнозів є параметричними в тому сенсі, що вони потребують виконання заданих припущень щодо властивостей математичного сподівання та дисперсії, чинних за умов нормальності відповідних розподілів. Наприклад, використовуючи MSE, ми неявно припускаємо, що всі похибки прогнозу мають однакові й постійні математичні сподівання та дисперсії. У реальних економічних ситуаціях найчастіше порушуються припущення гомоскедастичності та відсутності автокореляції. Можна стверджувати, що кожного разу прогноз будується у новій ситуації, отже, порівняння числової точності прогнозів, зроблених у різні моменти часу, не зовсім коректне. Наведені міркування зумовили використання непараметричних методів аналізу точності прогнозів.
Непараметричні методи аналізу точності прогнозів.
Непараметричні методи не залежать від вигляду розподілу, тож не потребують припущення щодо нормальності розподілів. Це особливо корисно, коли йдеться про дані, які унеможливлюють використання числових шкал. Розглянемо два типи непараметричних критеріїв: критерій знаків та рангові критерії.
Критерій знаків для порівняння точності двох послідовностей прогнозів базується на відсотку випадків, коли метод визначення прогнозу А кращий, ніж метод В. Таке порівняння здійснюють для індивідуальних прогнозів однакових подій (змінних). Якщо обидва методи дають однакову точність, імовірність відповіді «так» на запитання «чи прогноз А кращий за прогноз В» становить 0,5 для кожного з т випадків прогнозування. Число К випадків, коли прогноз А кращий, підпорядковано біноміальному розподілу ймовірностей
, (9.20)
Отже, можна підрахувати імовірність того, що К ≥ х. Якщо довжина послідовності прогнозів значна, для оцінювання ймовірностей можна використати нормальну апроксимацію біноміального розподілу.
Критерій знаків можна також використовувати для перевірки значущості описової статистики, відомої під назвою «відсоток кращих результатів», яка показує відсоток випадків, у яких один метод прогнозування кращий за інший і розраховується за формулою:
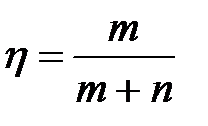, (9.21)
де m — кількість прогнозів, підтверджених фактичними даними;
n — кількість прогнозів, не підтверджених фактичними даними.
Коли всі прогнози підтверджуються, n = 0 і η = 1; якщо всі прогнози не підтвердилися, то m, а отже, і η дорівнюють 0.
Рангові критерії. У разі застосування цих критеріїв чисельна характеристика точності (абсолютна похибка, коли маємо один прогноз, або MSE, коли розглядають послідовність прогнозів) замінюється рангами, які потім перевіряють на значущість. Наприклад, якщо послідовності прогнозів показників А та В одержують за допомогою k методів, то спочатку обчислюють MSE, потім їхні значення ранжують від 1 (найменша MSE) до k (найбільша MSE) (відповідні ранги позначають через RA, та RB, для i = 1, …, k). Після знаходження різниць (dі) між рангами обчислюють коефіцієнт рангової кореляції Спірмена:
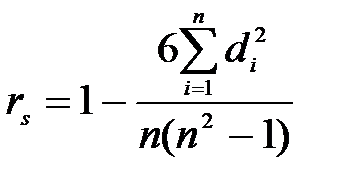, (9.23)
За нульову гіпотезу приймають відсутність залежності між рангами, тобто жоден з методів не є гіршим за решту. Гіпотеза відкидається, якщо значення rs досить велике.
Хоча непараметричні методи мають свої переваги, важливо усвідомлювати, що вони ігнорують частину доступної інформації. Так, критерії знаків та рангів не враховують числових значень похибок.
Дата: 2018-12-21, просмотров: 267.
